基于热分析动力学的烧结用焦炭颗粒燃烧数值模拟
王淦,温治, 2,楼国锋,曹欢
基于热分析动力学的烧结用焦炭颗粒燃烧数值模拟
王淦1,温治1, 2,楼国锋1,曹欢3
(1. 北京科技大学机械工程学院,北京,100083;2. 北京科技大学冶金工业节能减排北京市重点实验室,北京,100083;3. 中国石化工程建设有限公司,北京,100101)
基于烟气循环烧结中氧体积分数降低抑制了燃料燃烧,焦炭细化可显著改善整体燃烧效率,是烧结工艺极具潜力的节能增产措施,采用缩核模型,模拟贫氧率和粒度对焦炭颗粒燃烧特性的影响。焦炭的着火温度i、不完全燃烧系数、燃烧反应焓Δ等燃烧特性参数采用热重实验确定,焦炭燃烧的本征活化能和指前因子通过Flynn−Wall−Ozawa(FWO)法计算。研究结果表明:空气气氛中,焦炭颗粒的i约为550℃,为1.128~1.333,对应的Δ则为28.810~31.640 MJ/kg,约为137.156 kJ/mol;i基本上不随实验条件变化,随着氧体积分数的降低显著增大,则略减小;焦炭颗粒的最高燃烧温度约为1 560 K,燃烧速率随着灰层厚度的增加逐渐降低;当颗粒粒度增大或氧体积分数降低时,燃烧效率显著下降,且前者影响更大;考虑采用烟气循环,当焦炭细化效率达到1.33时,可保证整体燃烧效率不比传统烧结的低。
烧结;焦炭;颗粒燃烧;数值模拟;缩核模型;热重;动力学;Flynn−Wall−Ozawa法
与现行传统烧结工艺相比,烧结烟气循环技术减小了末端治理的负担,真正实现了烧结过程节能减排。国内自引进该技术以来,环保压力得到了有效缓解,然而,如何保证工艺产能成为一大新的难题。究其原因,主要是烧结用助燃气氧体积分数降低导致垂直烧结速度减小。燃料的粒度对烧结过程的燃烧特性具有重大影响,燃料细化工艺对于提高燃料燃烧效率进而实现烟气循环烧结工艺的节能增产具有重要意义,因此,必须开展针对烟气循环背景下烧结用焦炭燃烧特性的研究。研究单颗粒煤/焦的燃烧过程有助于深入掌握烧结料层内部的燃烧机理和特性。缩核模型[1]、随机孔模型[2]、分形增长模型[3]、CBK模型[4]和DAEM模型[5]等是模拟煤/焦燃烧中比较成熟的理论模型,此外,变化的孔隙结构参数已被广泛采纳[6−8]。作为多学科的通用分析测试手段,在近几十年来,热重技术已成为煤/焦燃烧特性分析的重要实验研究方法[9−12],普遍认为煤粉颗粒的细化对改善燃烧特性有显著作 用[9],在燃烧过程中,灰层厚度达到颗粒半径一半时灰层传质阻力最大[10],煤灰中的内在矿物质及其显微结构能极大地抑制燃烧过程[11]。以热重实验为基础的热分析动力学常用来计算煤/焦的动力学参数,典型的有Freeman-Carroll法[13]、Flynn−Wall−Ozawa(FWO)法[14]、Friedman−Reich−Lewi法[15]和Kissinger-Akahira- Sunose法[15−16]等。根据微分或积分近似的不同,采用上述方法所得计算结果略有差异[15]。然而,前人对煤/焦燃烧主要集中在纯理论研究,对与实际工业生产相结合的研究较少。同时,关键参数如焦炭的着火温度i、不完全燃烧系数、燃烧反应焓Δ等多取自经验值,随意性和普适性严重。为此,本文作者对某烧结用焦炭进行非等温热重实验,对比空气气氛与贫氧气氛下的化学反应特性差异,通过TG−DTG−DSC获得了焦炭的着火温度i,指前因子和燃烧反应焓Δ等燃烧特性参数,并采用FWO法计算燃烧反应动力学参数。在此基础上,将以上数据应用于开发的单颗粒焦炭燃烧缩核模型,重点研究氧体积分数和粒度对焦炭颗粒燃烧反应的影响。
1 烧结用焦炭的热重实验
1.1 样品准备
实验所用的焦炭取自国内某钢铁公司烧结厂现场,其原料为无烟煤。实验前,焦炭通过球磨和筛分,筛选粒度小于0.18 mm的细粉备用。在国家标准下完成焦炭的工业(GB/T 212—2001)和元素(GB/T 213—2003)分析,测试结果见表1。

表1 焦炭的工业分析及元素分析(干燥基,质量分数)
注:M为水分;A为灰分;V为挥发分。
1.2 实验设备及方法
实验采用法国SETARAM公司的LABSYS EVO ROBOT型同步热分析仪,并选取TG−DTG−DSC曲线进行分析。采用非等温实验,起始温度为室温,终止温度为1 400℃。升温速率分别为5,10和20 K/min,加热至终止温度后保温10 min,随后冷却。加热和保温阶段的载气为空气或贫氧气体,冷却阶段切换成N2,流量均为60 mL/min。鉴于烟气循环烧结技术的最低氧体积分数控制在15%,本实验中控制贫氧率(体积分数)分别为18%和15%,以N2为平衡气。焦炭样品质量为(15±0.2) mg,在相同条件下的实验均重复1次,以保证实验的复现性。
1.3 热重曲线分析
不同升温速率下焦炭燃烧的TG−DTG曲线见图1。由图1可知:不同升温速率下的TG曲线变化趋势相似;由于焦炭样品事先进行干燥处理且挥发分质量分数较低,故低于500 ℃的初始阶段TG曲线较平坦;进入剧烈燃烧阶段后,样品质量迅速下降;升温速率越高,焦炭中易燃组分和难燃物质的燃烧间隔越明显,此时DTG曲线存在2个明显的燃烧质量损失峰;随着升温速率减小,质量扩散和热量传递过程得到改善,焦炭的燃烧更加剧烈,易燃组分和难燃物质之间的燃烧界限变得模糊直至消失,DTG曲线仅出现1个质量损失峰。对比图1(a)~(c)可知:贫氧气氛下的TG曲线的剧烈燃烧阶段向高温区偏移;同时,DTG曲线的质量损失峰呈“矮胖”趋势发展,说明焦炭的燃尽时间延长,燃烧过程受到抑制。
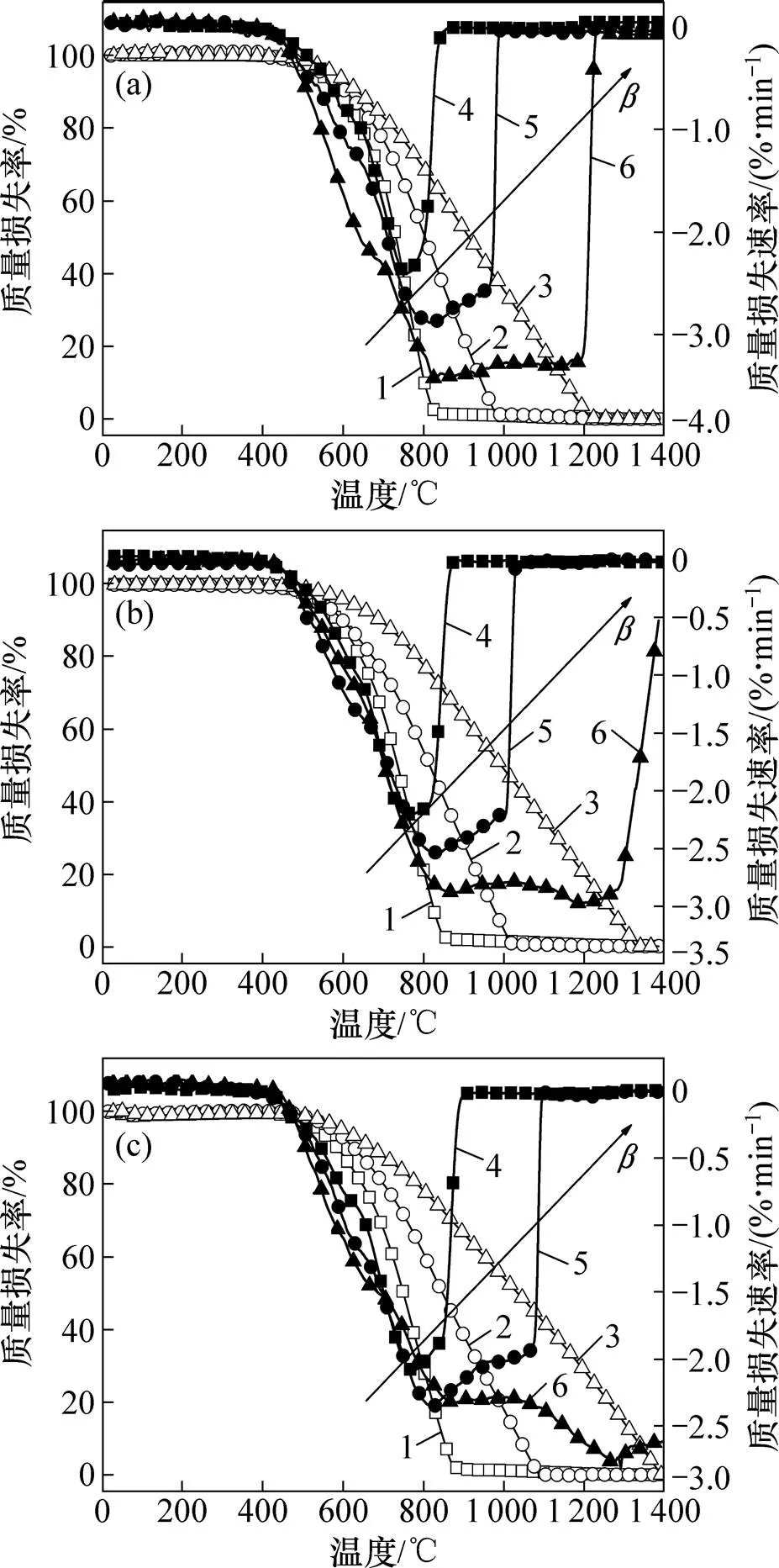
(a) 空气气氛;(b) 体积分数为18%的贫氧气氛;(c) 体积分数为15%的贫氧气氛1—TG,升温速率β为5 K/min;2—TG,升温速率β为10 K/min;3—TG,升温速率β为20 K/min;4—DTG,升温速率β为5 K/min;5—DTG,升温速率β为10 K/min;6—DTG,升温速率β为20 K/min。
着火温度i和燃尽温度t是描述焦炭燃烧特性的重要参数。本文中分别以燃烧过程初始阶段和结束阶段样品质量损失速率达到1%/min时刻的温度为i和b[19],见表2。由表2可知:在不同升温速率下,i略升高,载气气氛对i几乎无影响;而b随着升温速率的增加或氧体积分数的降低显著升高。这是因为i主要由样品本身的特性决定,而与升温速率及载气气氛无关;而热滞后现象随着升温速率的增大显著加剧,使样品内部温度梯度增大,反应更不充分,故对b造成重大影响;同时,氧体积分数降低,O2向反应界面的扩散过程受到抑制,进而影响燃烧速率,燃尽时间延长。
图2所示为热重实验对应的DSC曲线。根据DSC放热峰对时间积分可计算得焦炭燃烧的Δ及根据式(8)推导出,见表2。表2表明:氧体积分数降低抑制了O2与焦炭之间扩散,加剧了不完全燃烧现象,使Δ显著降低;同时,升温速率增大也将加剧不完全燃烧。
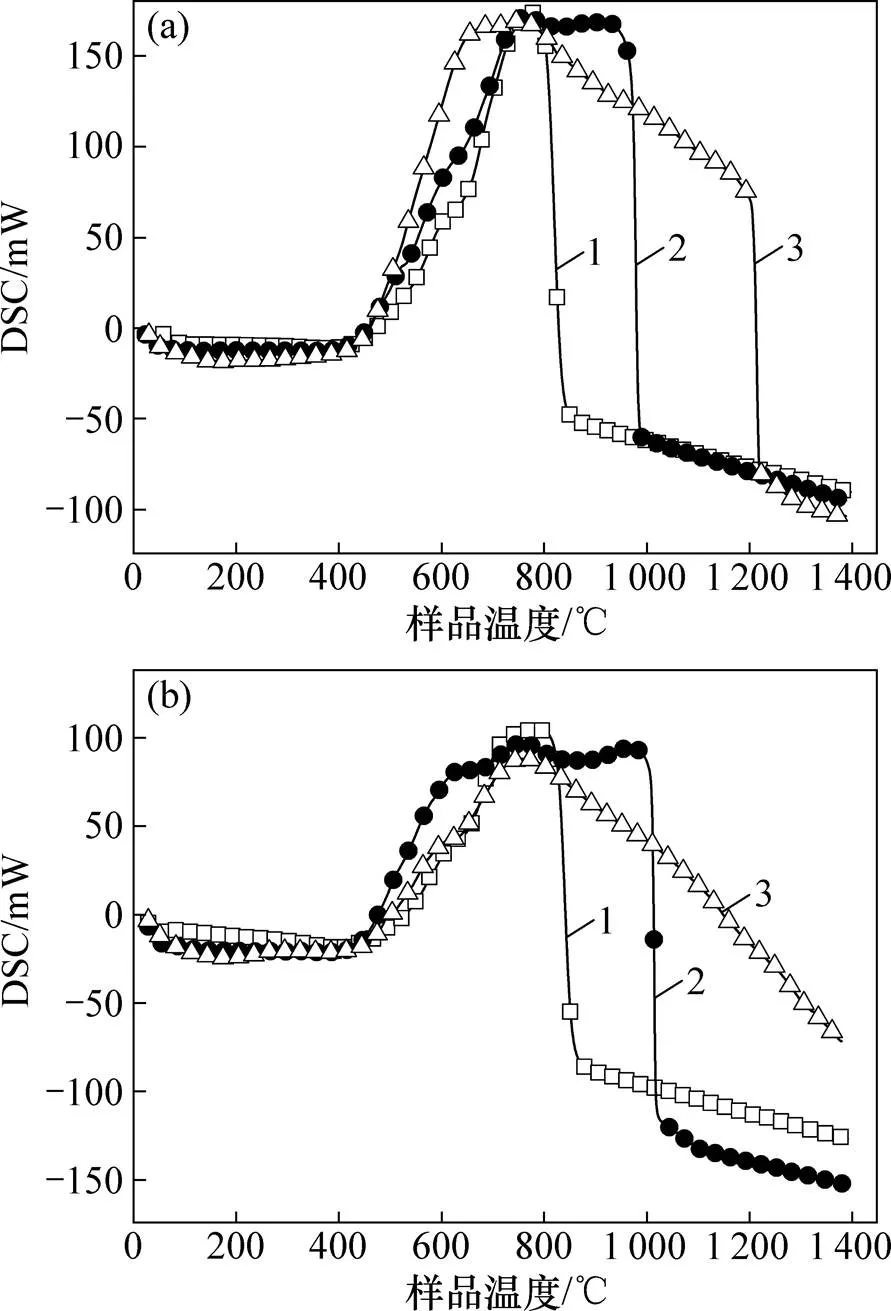
(a) 空气气氛;(b) 体积分数为18%的贫氧气氛升温速率/(K·min−1):1—5;2—10;3—20。
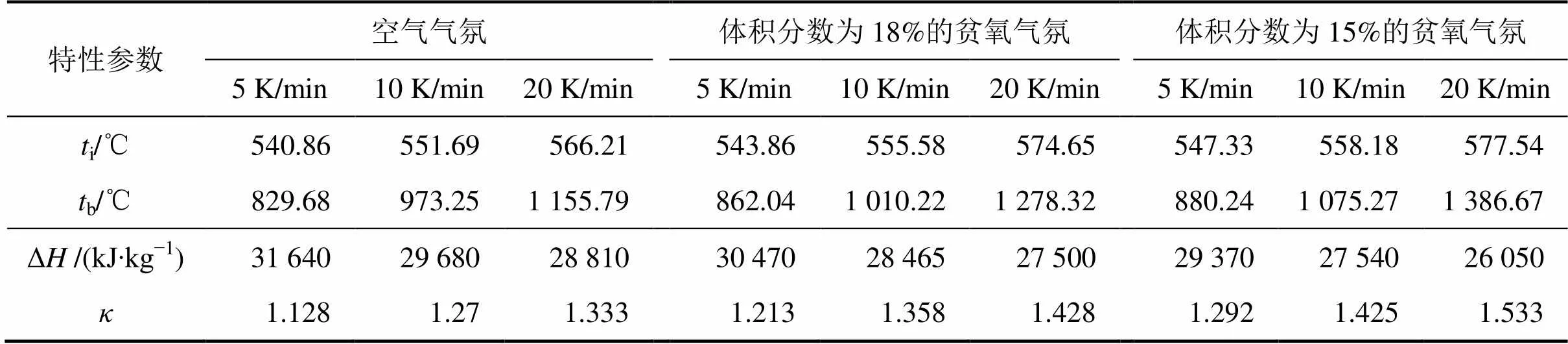
表2 不同气氛及升温速率下焦炭的燃烧特性参数
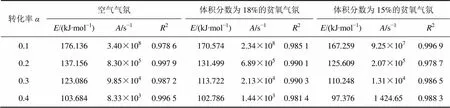
表3 Flynn−Wall−Ozawa法求得的焦炭燃烧动力学参数
1.4 燃烧动力学分析
本文的燃烧反应动力学参数用FWO法求取,具体推导过程参考文献[14]和[15],其表达式为
式中:为升温速率,K/min;为指前因子,s−1;为活化能,kJ/mol;为气体摩尔常数,8.314 J/(mol∙K);()为积分形式的机理函数,采用球对称收缩核模型,()=1−(1−)1/3;为热力学温度,K;为燃烧转化率,通过=(0−)/(0−t) 计算;0,t和分别为样品的原始质量、反应结束后残渣的质量和反应中瞬时质量,mg。
对于不同的,选择相同的,则()是1个恒定值。通过ln对1/作图拟合1条直线,从斜率可以求出随不同反应深度变化的系列值。鉴于在化学反应动力区求得的动力学参数才能准确描述样品的本征反应特性[11],本文仅计算焦炭燃烧反应在转化率为0.1~0.4时的和,如表3所示。
表3表明:FWO法计算的和具有很好的线性关系系数2基本在0.99以上,证明了结果的可靠性;同时,焦炭燃烧反应的活化能随反应的深入逐渐降低。LIU[15]指出:随着燃烧反应进行,焦炭表面炭灰逐渐加厚,空气扩散到焦炭表面的过程对整个焦炭燃烧的影响逐渐加剧,导致焦炭燃烧反应的活化能出现逐渐降低的趋势;同时,贫氧气氛下的活化能比空气气氛下的略小,这也与MUNIR等[18]的研究成果具有相同的变化规律。
在较低的转换率(=0.2)时,扩散作用对燃烧过程基本无影响,此时,FWO法计算的活化能与文献[22]中的基本一致[19]:对于无烟煤/焦,= 137.58~147.22 kJ/mol。HURT等[19]指出,目前普遍认为全球的煤/焦燃烧活化能一般在105~180 kJ/mol之间,而多数在130~150 kJ/mol范围内。因此,本文中焦炭燃烧的本征活化能取137.156 kJ/mol(空气气氛)、131.499 kJ/mol(体积分数为18%的贫氧气氛) 以及125.609 kJ/mol(体积分数为15%的贫氧气氛)是可信的。
2 焦炭颗粒燃烧数值模型
2.1 物理模型
在抽风烧结过程中,沿整个料层高度上将呈现性质不同的5个区域,从上到下分别为烧结矿带、燃烧带、预热带、干燥带和过湿带。燃烧带的厚度一般仅为20 mm,并以10~40 mm/min的速度往下迁移。焦炭颗粒在燃烧带内部的燃烧特性对整个烧结过程有重要影响。烧结用焦炭颗粒的粒度跨度较大,当量粒度为1.5~2.0 mm,其燃烧过程必须考虑气膜传质扩散、灰层扩散、界面化学反应等因素的综合影响。因此,在本文中将焦炭颗粒的燃烧反应模型假设为广泛采用的球对称收缩核模型,其燃烧过程示意图见图3。
2.2 简化假设
结合热重实验条件,颗粒燃烧模型假设如下: 1) 焦炭颗粒处于无限大空间,环境温度保持不变; 2) 颗粒内部处于局部热平衡状态,忽略气−固间的温差;3) 颗粒内部热量传递以导热为主,忽略扩散和辐射;4) 氧气扩散到颗粒表面,并通过气膜和孔隙深入到核内部;5) 在反应过程中颗粒粒度保持不变;6) 反应在炭灰和焦核之间的界面上进行;7) 反应产生的炭灰不脱落,包围在焦核的周围。
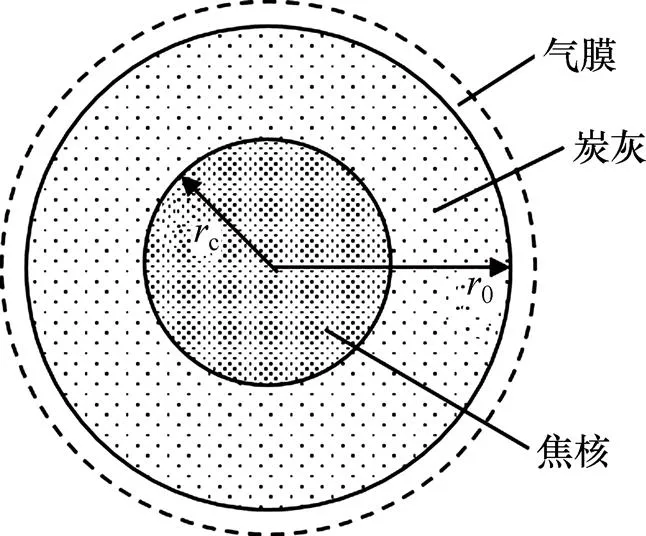
图3 焦炭颗粒燃烧过程示意图
2.3 数学模型
根据2.2节的假设条件,确定焦炭颗粒的传热方程为
根据质量守恒定律,焦炭颗粒质量变化等于燃烧质量消耗,其数学表达式为
式中:为颗粒孔隙率,对焦炭,0=0.39,对炭灰,ash=0.54;为颗粒密度,对焦炭,0=980 kg/m3,对炭灰,ash=700 kg/m3;c为颗粒比热容,对焦炭,p,0= 1 638.7 J/(kg∙K),对炭灰,p,ash=836.4 J/(kg∙K);为反应时间,s;为颗粒半径,m;eff为有效导热系数,W/(m∙K),通过eff=2∙计算;为颗粒热导率,对焦炭,0=0.153 W/(m∙K),对炭灰,ash=0.116 W/(m∙K);m为焦炭摩尔质量,c=0.012 kg/mol;C为颗粒的界面燃烧速率反应速率,mol/s;Δ为化学反应焓,为26 050~31 640 J/g;C为焦核半径(当前反应半径),m。
2.3.2 定解条件
1) 初始条件:0= 298 K,f=1473 K,= 1100 kg/m3。
2) 边界条件:
式中:0为初始时刻颗粒温度,K;f为环境温度,K;0为初始时刻颗粒半径,m;为对流换热系数,W/(m2∙K),通过=∙g/p计算;g为气体导热系数,W/(m∙K);p为焦炭颗粒当量粒度,m,p= 20;为努塞尔数,通过=[2+(0.40.5+0.060.667)∙0.4(μ/)0.25]计算;为雷诺数;为普朗特数;μ和分别为环境中和颗粒表面气体的动力黏度,Pa∙s;s为颗粒外表面温度,K;m为黑度,m=0.8;为Stefan-Boltzmann常数,=5.67×10−8W/(m2∙K4)。
3 内热源项Rc·ΔH的确定
在研究焦炭燃烧模型时,大多数学者将其视为完全燃烧模式。事实上,烧结过程中的燃烧过程为由多个基元反应组成的混合反应。文献[1]提出了如下综合反应方程式:
C+O2=2(−1)CO+(2−)CO2(6)
式中:为不完全燃烧系数,=1.13~1.53。因而,燃烧反应的总体反应焓和燃烧速率可通过以下2式确定:
Δ=2(−1)∙Δ1+(2−)∙Δ2(7)
c=∙m/O2∙4πr2∙C∙O2(8)
式中:Δ1为C+O2=CO2的燃烧反应焓,33 411 J/g;Δ2为C+0.5O2=CO的燃烧反应焓,9 797 J/g;O2为氧气摩尔质量,0.032 kg/mol;C为综合反应速率常数,m/s,通过C=1/(1/m/eff∙O2+1/c)计算;O2为环境氧浓度,mol/m3;m为气膜传质系数,m/s,通过k=∙CO2/p计算;为舍伍德数,通过=2+0.70.71/3计算;为炭灰层厚度,m,=0−r;eff为有效孔隙率,通过eff=0∙e−0.006Bδ计算;O2和CO2分别为氧气和二氧化碳的扩散系数,m2/s,分别通过O2=2.03×10−51.87和CO2=7.181×10−81.75计算;c为化学反应速率常数,m/s,通过c=∙0.5∙e−E/(RT)计算。为反应活发能,=125.61~137.16 kJ/mol;为指前因子,=(6.89~8.30)×105s−1。
4 焦炭颗粒燃烧模拟分析
4.1 燃烧转化率和速率
图4所示为焦炭颗粒的燃烧转化率和燃烧速率随量纲一反应时间的变化曲线。从图4可以看出:在燃烧初始阶段,反应发生在颗粒表面,反应速率急剧增加,转化率曲线变化较快;随后,由于燃烧向颗粒内部发展,颗粒燃烧速率下降,质量消耗率降低,转化率曲线变化逐渐趋于平缓。综合而言,导致燃烧速率下降的原因主要有:1) 燃烧界面的氧浓度由于外层炭灰的阻挡逐渐降低;2) 燃烧导致颗粒温度较高,与外界温差显著,对流换热加强,导致颗粒温度降低; 3) 燃烧界面逐渐向颗粒内部迁移,有效反应面积减小。
4.2 焦炭颗粒内部温度
图5所示为燃烧过程中焦炭颗粒度向不同位置的温度变化曲线,其中′为颗粒的量纲一半径,′=0为颗粒中心位置,′=1则为颗粒外表面点。随着时间变化,颗粒内部温度呈现不同的变化趋势。在燃烧前的加热阶段(<0.47),颗粒内部的温度梯队出现先增大后减小的过程;在初始阶段(<0.1),颗粒外表面与环境温差大,对流及辐射换热强烈,升温剧烈。同时,外表面向内部导热,而由于导热作用远小于外表面与环境的热量交换,颗粒内部的温差逐渐增大。当颗粒外表面温度继续升高时(>0.2),外表面与环境的热交换削弱,内部导热逐渐增强,升温加快,内外温度梯度减小。达到着火温度后,燃烧产生的热量使得颗粒温度在极短的时间内(=0.47~0.50)急速升高,最终在≈0.65时达到最高温度(约1 560 K)。此后,由于焦核逐渐缩小,燃烧速率逐渐降低,且反应界面始终向内外两侧传递热量,导致颗粒温度出现下降趋势。由于煤焦的导热能力远比炭灰的大,因而,焦核的温度比较均匀,炭灰层的温度梯度则较大。
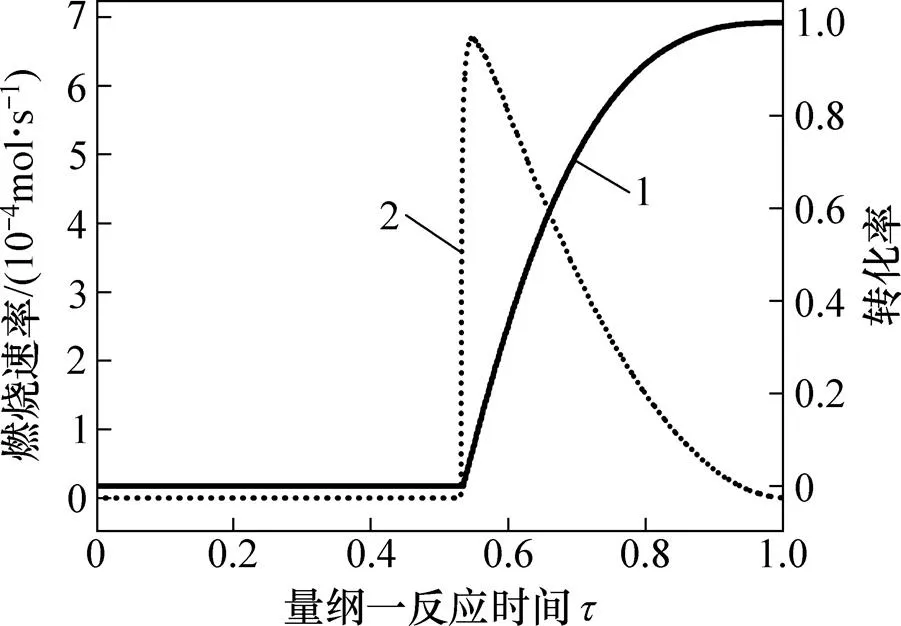
1—转化率;2—燃烧速率。
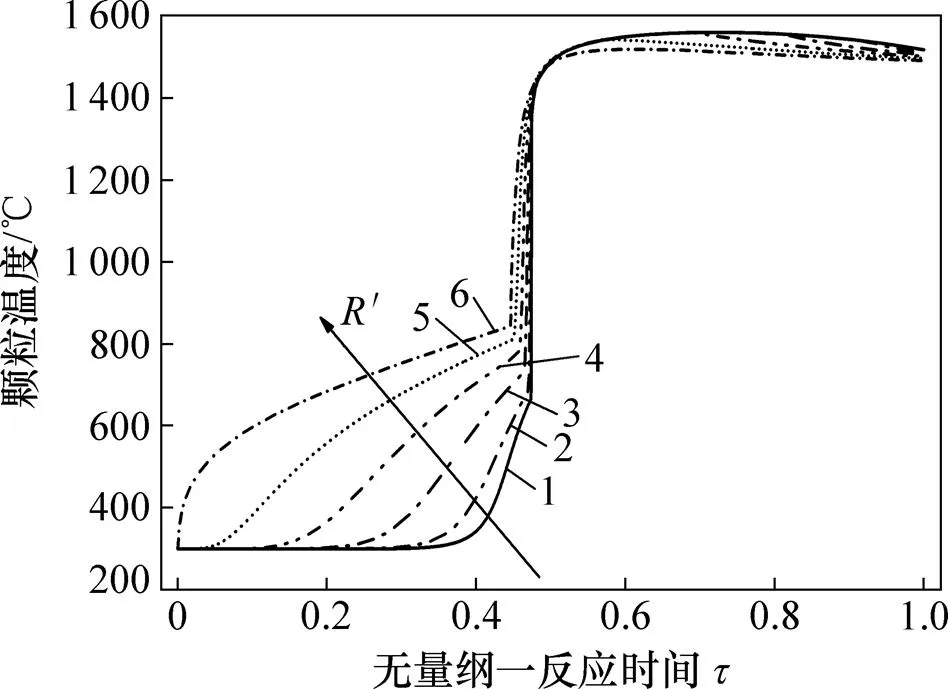
R′:1—0;2—0.2;3—0.4;4—0.6;5—0.8;6—1.0。
4.3 影响因素分析
在烧结过程中,操控参数对于燃烧带有重要影响,不同的环境条件和焦炭品位直接决定了燃烧带的温度、烧结时间以及热量供应效率。通过研究单颗粒焦炭的燃烧情况,针对颗粒本身和环境条件的变化进行模拟讨论,有利于烧结过程的改进。本文的模拟参数如表4所示,以粒度为2.0 mm、氧体积分数为21%为参考工况。

表4 模拟参数取值
4.3.1 焦炭粒度的影响
颗粒粒度对燃烧过程的影响如图6所示。从图6可见:随着粒度减小(氧体积分数保持在21%),燃烧界面的有效反应面积显著减小,因此,单颗粒的燃烧速率显著降低;随着颗粒当量直径从2 mm逐渐减小至1.0 mm,最大燃烧速率从1.99×10−4mol/s分别降低至1.66×10−4,1.34×10−4,1.03×10−4和0.75×10−4mol/s。但对于单位质量的焦炭燃烧,若粒度从2 mm减小至1.0 mm,则整体燃烧速率反而升高了3倍;同时,当粒度降低时,颗粒吸收热量使整体达到燃烧温度所需时间显著降低,且在燃烧后期,颗粒外侧炭灰对CO2和O2扩散的影响逐渐消失,故焦炭的燃尽时间显著缩短;当颗粒粒度从2 mm降低至1 mm时,燃尽时间缩短66.67%(从1.35 s缩短至0.45 s),这说明细化焦炭能极大地促进了烧结料层中焦炭的燃烧过程。在实际烧结过程中,为了提高焦炭的燃烧效率,进而改善烧结矿品质,应优选平均粒度小的焦炭。
4.3.2 贫氧率的影响
不同贫氧率(粒度保持2 mm)下焦炭燃烧反应速率如图7所示。由图7可知:氧体积分数变化对焦炭着火点的影响可以忽略;环境氧体积分数21%时,最大燃烧反应速率为1.99×10−4mol/s,当氧体积分数降低至18%和15%时,最大燃烧速率分别降低至1.72× 10−4和1.44×10−4mol/s,即燃烧速率随着氧体积分数下降呈近似线性降低;同时,燃尽时间从1.35 s分别延长至1.58 s和1.91 s。当周围环境氧体积分数较高时,通过炭灰层扩散到燃烧界面的氧通量更多,给燃烧反应提供了相对更充分的氧气,提高了燃烧速率;而氧体积分数越低,对焦炭燃烧的抑制作用越强。在引入烟气循环烧结技术时,应尽量控制循环烟气的氧体积分数与空气中的接近。
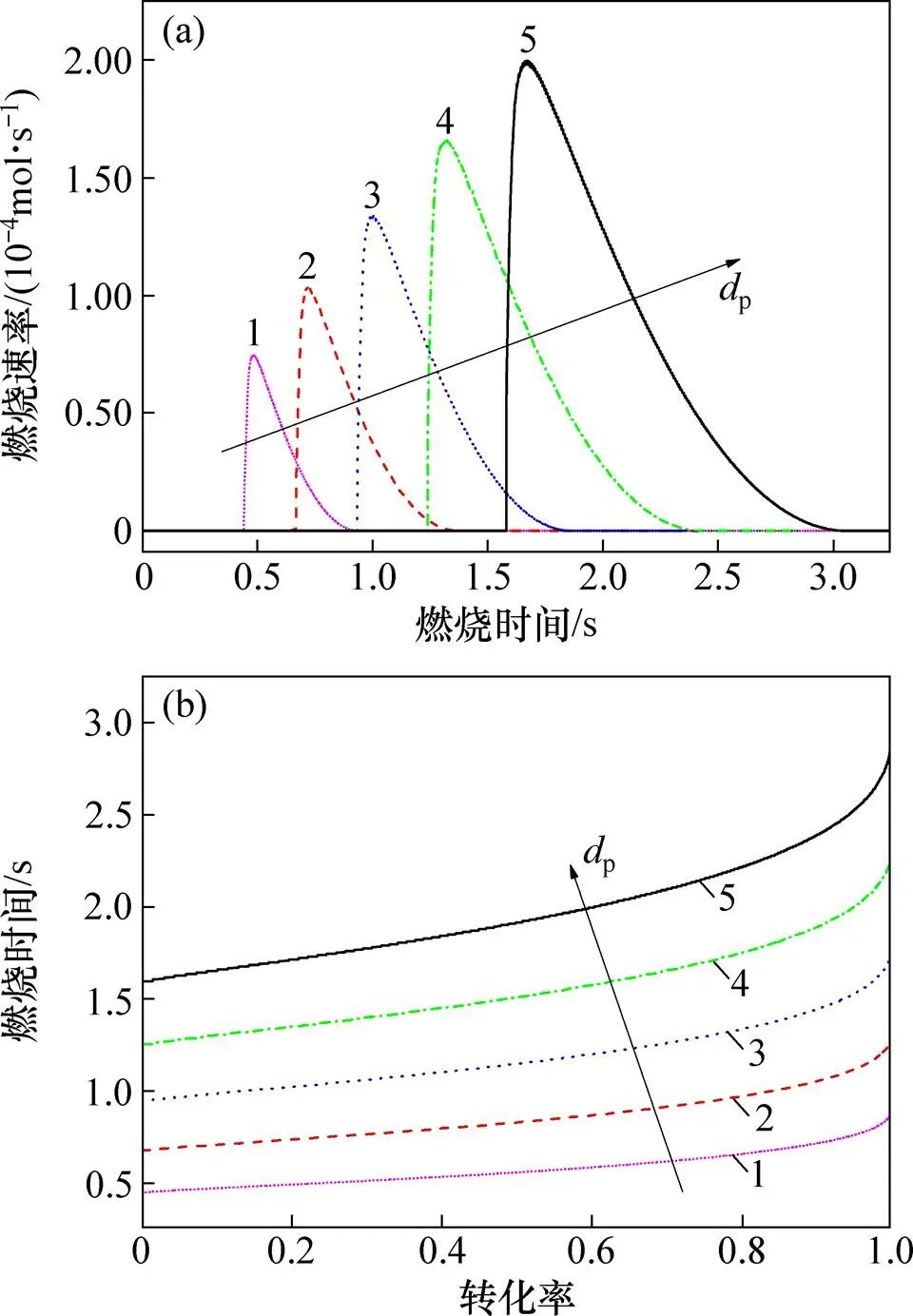
(a) 燃烧速率;(b) 转化率dp/mm:1—1.00;2—1.25;3—1.50;4—1.75;5—2.00。
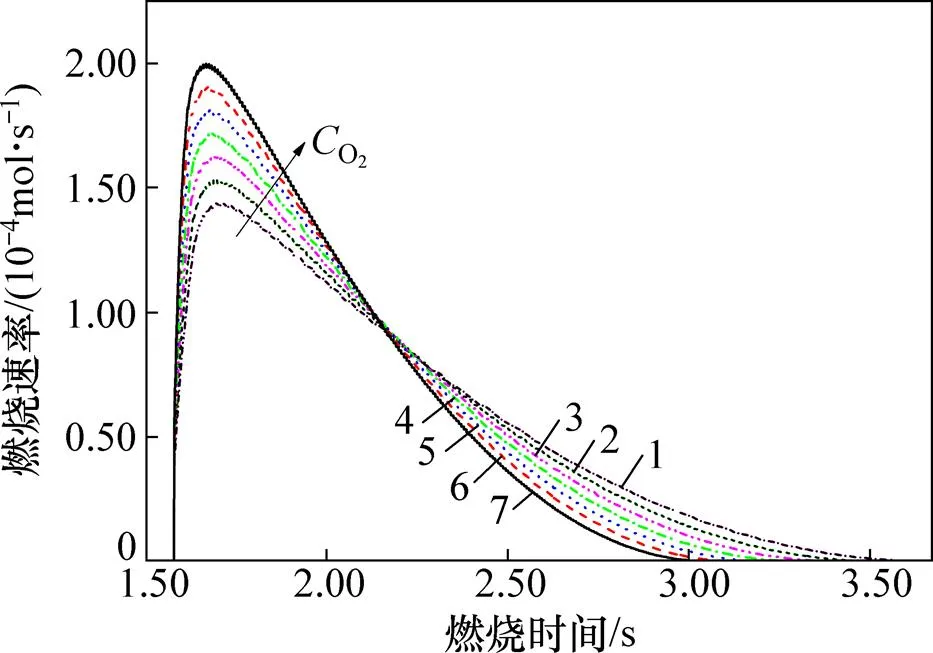
O2体积分数/%:1—15;2—16;3—17;4—18;5—19;6—20;7—21。
4.3.3 焦炭细化效率的确定
定义参考粒度与细化粒度的比值为焦炭细效率。采用烟气循环技术时,助燃气氧体积分数降低是一个不可避免的问题。本文以单位质量焦炭的燃尽时间和最大燃烧速率为指标,以确定不同氧体积分数时的。分析表5发现:相比于氧体积分数,焦炭粒度的影响更显著;当氧体积分数高于17%时,粒度细化至1.75 mm时即可保证整体燃烧效率不降低,此时,=1.14;当氧体积分数低于17%时,则需细化至1.5 mm,=1.33。当然,细化粒度越小,越大,对焦炭燃烧的促进越显著。然而,考虑到控制生产成本,无法实现焦炭的超细化。目前,烧结用焦炭的当量粒度控制在1.5~2.0 mm,因此,合理筛选小粒度的焦炭即可满足实际烟气循环工艺的需要。
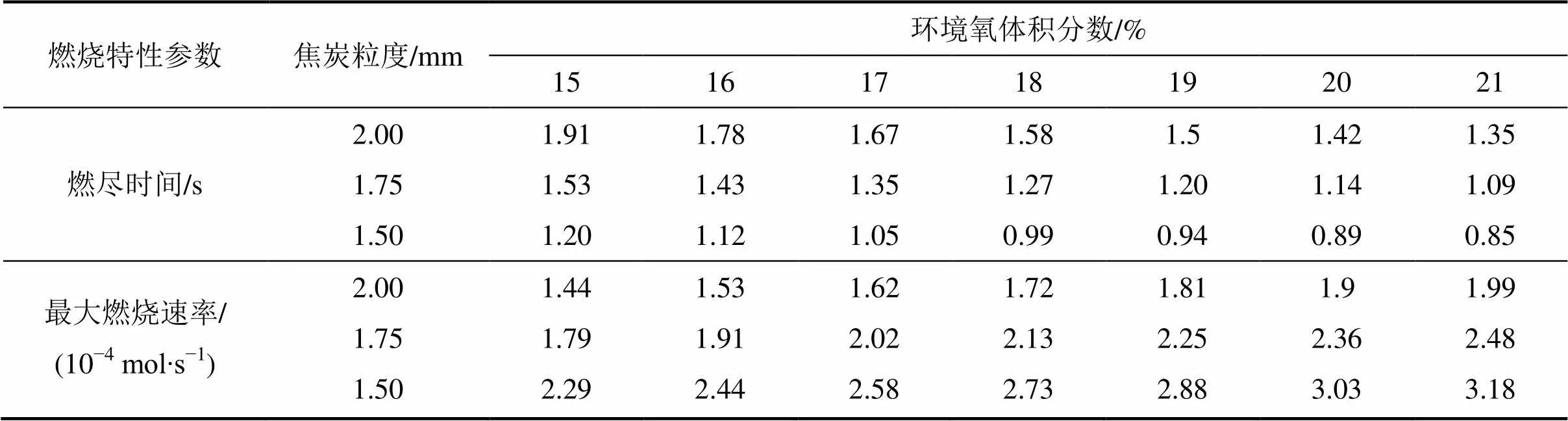
表5 不同氧体积分数与粒度下的单位质量焦炭燃尽时间和速率关系
5 结论
1) 焦炭燃烧的i由样品本身特性决定,约为 550℃。在热重实验中,热滞后性的存在使i随着升温速率的增加略有升高;随着氧体积分数降低,不完全燃烧程度增加,在1.128~1.333之间,对应的Δ为28.810~31.640 J/g;空气和贫氧气氛下的分别为137.156,131.499 和125.609 kJ/mol。
2) 以热重实验确定了数值模拟的关键参数。焦炭燃烧能达到的最高温度为1 560 K;在燃烧前的加热阶段,颗粒内部温度梯度呈先增大后减小的趋势;燃烧开始后,焦核内温度相对均匀,炭灰层内则存在较大温度梯度。
3) 焦炭单颗粒的燃烧速率和燃尽时间均随粒度减小而显著降低;若考虑单位质量焦炭的燃烧,当量直径为1 mm的焦炭整体燃烧速率为2 mm时的3倍。同时,燃烧速率随着环境氧体积分数下降呈近似线性降低,燃尽时间相应延长。粒度的影响比氧体积分数的影响更显著。在实际烟气循环烧结过程中,当焦炭细化效率达到1.33时,即可保证整体的燃烧效率与传统烧结工艺相当。
参考文献:
[1] SADHUKHAN A K, GUPTA P, SAHA R K. Modelling of combustion characteristics of high ash coal char particles at high pressure shrinking reactive core model[J]. Fuel, 2010, 89(1): 162−169.
[2] 费华, 胡松, 向军, 等. 随机孔模型研究煤焦O2/CO2燃烧动力学特征[J]. 化工学报, 2011, 62(1): 199−205. FEI Hua, HU Song, XIANG Jun, et al. Kinetics of coal char combustion with random pore model under O2/CO2Atmosphere[J]. Journal of Chemical Industry and Engineering (China), 2011, 62(1): 199−205.
[3] LIU Yuting, HE Rong. Variation of apparent reaction order in char combustion and its effect on a fractal char combustion model[J]. Combustion Science and Technology, 2015, 187(10): 1638−1660.
[4] GHAREBAGHI M, IRONS R M, POURKASHANIAN M, et al. An investigation into a carbon burnout kinetic model for oxy–coal combustion[J]. Fuel Processing Technology, 2011, 92(12): 2455−2464.
[5] CAPRARIIS B, FILIPPIS P, HERCE C, et al. Double-gaussian distributed activation energy model for coal devolatilization[J]. Energy & Fuels, 2012, 26(10): 6153−6159.
[6] WANG Fuyang, BHATIA S K. A Generalized dynamic model for char particle gasification with structure evolution and peripheral fragmentation[J]. Chemical Engineering Science, 2001, 56(12): 3686−3697.
[7] SADHUKHAN A K, GUPTA P, SAHA R K. Analysis of the dynamics of coal char combustion with ignition and extinction phenomena:shrinking core model[J]. International Journal of Chemical Kinetics, 2008, 40(9): 569−582.
[8] ALVAREZ L, GHAREBAGHI M, POURKASHANIAN M, et al. CFD modelling of oxy-coal combustion in an entrained flow reactor[J]. Fuel Processing Technology, 2011, 92(8): 1489−1497.
[9] CANGIALOSI F, CANIO F, INTINI G, et al. Combustion reactivity of unburned carbon in coal combustion fly ashes[C]//2005 World of Coal Ash (WOCA). Lexington, Kentucky, USA: 2005: 347−352.
[10] 旷戈, 张济宇. 恒温热重法单颗粒煤焦燃烧动力学[J]. 化工学报, 2006, 57(1): 140−145. KUANG Ge, ZHANG Jiyu. Single coal particle combustion characteristics and kinetics study using thermogravimetric method under constant temperature[J]. Journal of Chemical Industry and Engineering (China), 2006, 57(1): 140−145.
[11] KELEBOPILE L, SUN Rui, LIAO Jian. Fly ash and coal char reactivity from thermogravimetric(TGA) experiments[J]. Fuel Processing Technology, 2011, 92(6): 1178−1186.
[12] QIAN Wei, XIE Qiang, HUANG Yuyi, et al. Combustion characteristics of semi-cokes derived from pyrolysis of low rank bituminous coal[J]. International Journal of Mining Science and Technology, 2012, 22(5): 645−650.
[13] LIAO Yanfen, MA Xiaoqian. Thermogravimetric analysis of the CO-combustion of coal and paper mill sludge[J]. Applied Energy, 2010, 87(11): 3526−3532.
[14] SEO D K, PARK S S, KIM Y T, et al. Study of coal pyrolysis by thermogravimetric analysis(TGA) and concentration measurements of the evolved species[J]. Journal of Analytical and Applied Pyrolysis, 2011, 92(1): 209−216.
[15] LIU Hao. Combustion of coal chars in O2/CO2and O2/N2Mixtures: a comparative study with non-isothermal thermogravimetric analyzer (TGA) tests[J]. Energy and Fuel, 2009, 23(9): 4278−4285.
[16] WANG Chang’an, ZHANG Xiaoming, LIU Yinhe, et al. Pyrolysis and combustion characteristics of coals in oxy-fuel combustion[J]. Applied Energy, 2012, 97: 264−273.
[17] WANG J H, CHANG L P, LI F, et al. A study on the combustion properties of western chinese coals[J]. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2010, 32(11): 1040−1051.
[18] MUNIR S, DAOOD S S, NIMMO W, et al. Thermal analysis and devolatilization kinetics of cotton stalk,sugar cane bagasse and shea meal under nitrogen and air atmospheres[J]. Bio-resource Technology, 2009, 100(3): 1413−1418.
[19] HURT R H, CALO J M. Semi-global intrinsic kinetics for char combustion modeling[J]. Combustion and Flame, 2001, 125(3): 1138−1149.
(编辑 陈灿华)
Numerical simulation on combustion characteristics of sintering used coal char particle based on thermo-gravimetric kinetic analysis
WANG Gan1, WEN Zhi1, 2, LOU Guofeng1, CAO Huan3
(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;2. Beijing Key Laboratory of Energy Saving and Emission Reduction for Metallurgical Industry,University of Science and Technology Beijing, Beijing 100083, China;3. SINOPEC Engineering Incorporation, Beijing 100101, China)
In flue gas recirculation sintering technology, the reduction of oxygen content in the recirculated flue gas significantly inhibits the combustion characteristics of the coal char, and refining coke can significantly accelerate coke combustion rate with the increase of the surface area, which can effectively save energy. The influence of oxygen contents (oxygen-lean) and particle sizes on combustion characteristics of the sintering used coal char particle was numerically simulated. The unreacted-core shrinking model was employed. The ignition temperaturet, incomplete combustion coefficientand reaction enthalpy Δof the coal char were determined by thermo-gravimetric technology, while the intrinsic activation energyand pre-exponential factorwere calculated in different heating rates with Flynn−Wall−Ozawa (FWO) method. The results show thatiof coal char is about 550℃ in air atmosphere;increases from 1.128 to 1.333 when heating rate increases, while Δdecreases from 28.810 kJ/kg to 31.640 MJ/kg, respectively,is about 137.156 kJ/mol.ihardly changes with the change of experimental conditions, whilesignificantly increases with the decrease of oxygen volume fraction, andshows the opposite trend. In the numerical simulation, the maximum temperature of char particle in combustion process is 1 560 K. During combustion, ash layer thickness gradually increases, resulting in decrease of the reaction rate of particle. The combustion efficiency decreases significantly when particle size increases or the oxygen content decreases, on which the effect of the former is more obvious. The refining efficiency of coal char is suggested to be 1.33,when flue gas recirculation sintering technology is applied, aiming at a consistent overall combustion efficiency compared to the conventional sintering process.
sintering; coal char; particle combustion; unreacted-core shrinking model; numerical simulation; thermo-gravimetric; kinetic analysis; Flynn−Wall−Ozawa method
10.11817/j.issn.1672-7207.2016.10.005
TF526+.1
A
1672−7207(2016)10−3315−08
2015−11−20;
2016−01−22
国家自然科学基金资助项目(50876011)(Projects(50876011) supported by the National Natural Science Foundation of China)
楼国锋,副教授,从事燃烧、非平衡态等离子体性质及利用研究;E-mail:lgf@ustb.edu.cn

