基于CLAHE和图像分解的去雾方法

黎秀玉，宋树祥，夏海英

(广西师范大学电子工程学院， 广西桂林541004)



基于CLAHE和图像分解的去雾方法

黎秀玉，宋树祥，夏海英

(广西师范大学电子工程学院， 广西桂林541004)

针对雾天条件下拍摄到的图像对比度低、细节模糊以及颜色暗淡的现象，提出一种基于CLAHE和图像分解的去雾方法。首先，采用限制对比度直方图均衡化(limited contrast histogram equalization，CLAHE)对有雾图像进行增强，有效地提升图像的对比度；然后，在照明—反射模型的基础上，根据照射分量与反射分量的不同特征对增强后的图像进行梯度滤波，将图像进行分解，获得最终包含图像所有细节的反射图像；最后，对反射图像进行Gamma变换，提升图像的亮度，获得最终的去雾图像。利用信息熵、空间频率、平均梯度和运算时间等客观评价标准，与带色彩恢复多尺度Retinex算法(MSRCR算法)和基于暗通道先验去雾算法(He算法)进行对比。实验结果的主观评价和客观评价表明，在雾天图像细节增强和色彩保持方面，本文方法比MSRCR算法和He算法具有更好的效果。

图像去雾；CLAHE；图像分解；反射分量；图像复原

0 引 言

在雾天条件下，空气中的悬浮颗粒的散射作用会导致采集图像的对比度降低、可视性差，这对视频监控、目标跟踪、智能交通、航拍和遥感等室外图像处理系统的性能造成极大的影响和限制。因此，对图像进行去雾显得非常有实际意义。

对雾天图像的清晰化处理一般有两大类方法：一是基于物理模型的方法[1-3]，需要建立图像退化模型，然后对其进行逆推导，求出模型中相对应参数，最终恢复出无雾图像；二是基于图像增强的方法，通过提高对图像感兴趣区域的对比度来达到图像清晰化目的。目前雾天图像增强方法主要包括直方图均衡化和Retinex的相关算法。全局直方图均衡化算法(HE)[4-5]简单且易于实现，但是忽略了场景深度的变化，增强后的图像效果往往不理想。局部直方图均衡化(AHE)[6]可以实现图像局部区域的增强，但是容易出现块状现象且其计算量大。限制对比度直方图均衡化(CLAHE)[7-8]是对这两种直方图均衡化的一种改进，既继承了前述两种直方图均衡化方法的优点，同时还能有效地抑制噪声。Retinex算法[9-11]的基本思路是把一幅图像看成由入射分量和反射分量组成，然后采用某种途径计算出反射分量，实现对图像的增强。该算法一般利用高斯卷积模板进行照度估计，不具备边界保持能力，导致在像素值变化剧烈的边界区域产生光晕现象，尤其是在图像光照突变、明暗对比强烈的边缘区域最为明显。图像分解方法[12]同样建立在照明—反射模型的基础上，通过利用照射分量与反射分量的不同特征直接将图像进行分解，从而获得包含图像细节的反射分量。本研究在此基础上采用CLAHE算法与图像分解算法相结合来实现对图像进行增强，旨在提高图像的对比度，保持图像的色彩信息，消除光晕现象，使复原后的图像具有较好的视觉效果。

1 限制对比度自适应直方图均衡化

限制对比度自适应直方图均衡化(CLAHE)算法通过增强局部区域对比度使图像细节清晰化。CLAHE算法基本流程[13-14]：

①将原图像分割为M×N个连续且互不重叠的子区域；

②用预先定义的阈值对每个子区域的灰度直方图进行裁剪，将超出阈值的像素进行重新分配，如图1所示；

③对限制对比度后的每个子区域进行灰度直方图均衡化；

④获取每个子区域中心点，将这些点作为线性插值样本点；

⑤对图像的每一个像素进行线性插值运算，如图2所示。

(a) 直方图的剪切 (b) 像素的重新分配

图1 直方图的剪切以及重新分配

Fig.1 Shear of histogram and redistribution

CLAHE通过在计算转化函数前用预先定义的阈值来裁剪直方图以达到限制放大幅度的目的。首先将图像分为若干个子区域，依次分别计算每个子区域的直方图，然后对每个子区域进行直方图裁剪(如图1所示)，把那些超出直方图剪切阈值的部分均匀分配到直方图的其他部分。

从图1可以看出，经过这种再分配的过程可能会导致直方图中另一部分再次超过了裁剪值(如图1中右边直方图中顶层的阴影部分所示)。为解决该问题，通过递归重复再分配过程，直到多余的部分可以忽略不计为止。

在图2中，由白色标记的中心区域像素值可以通过双线性插值的方法求解(如图3所示)，由斜阴影标记区域的像素值采用线性插值的方法计算，位于图像四个角点处由黑点标记的像素值可以直接通过其所在子图像的变换函数来获取。

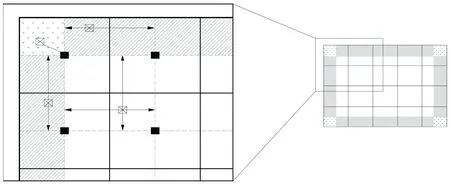
(a) 线性插值的局部放大示意图 (b) 线性插值示意图

图2 CLAHE的线性插值示意图

Fig.2 Schematic diagram of linear interpolation of CLAHE

图3 双线性插值计算示意图

如图3所示，f(x1,y1)，f(x2,y1)，f(x1,y2)，f(x2,y2)分别表示A，B，C，D点处的像素值，则插值点处的像素值f(x,y)可表示为：

f(x,y)=a[bf(x1,y1)+(1-b)f(x2,y1)]+(1-a)[bf(x1,y2)+(1-b)f(x2,y2)],

(1)

(2)

(3)

2 图像的分解

一幅给定的图像可以由两个分量来表征：一是入射到被观察场景的光源照射分量。二是场景中物体反射的光照总量。这两个分量分别称为入射分量和反射分量，分别表示为L(x,y)和R(x,y)。两个分量的乘积形成图像 ，即：

S(x,y)=L(x,y)R(x,y)，

(4)

对式(4)两边取对数得：

logR(x,y)=logS(x,y)-logL(x,y)，

(5)

将式(5)简化得:

IR=I-IL。

(6)

图像的照射分量通常由慢的空间变化来表征，而反射分量往往引起突变，特别是在不同物体的连接部分，所以照射分量要比反射分量要平滑[15]。Li等[16]根据这个性质提出假设，图像中梯度大的属于反射分量IR，梯度小的属于入射分量IL，建立反射分量IR和入射分量IL的概率模型，分别表示如下：

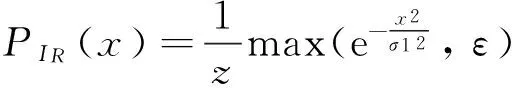
(7)

(8)

其中，x表示梯度值，z是归一化因子，σ1和σ2是两个高斯滤波器的参数，ε是一个很小的数，用于防止PIR(x)趋于0。

为了使两个分量分离，需将P(IR,IL)进行最大化，可通过对P(IR,IL)求负对数的最小值来使其达到最大化。分别对式(7)和式(8)取负对数，得：

(9)

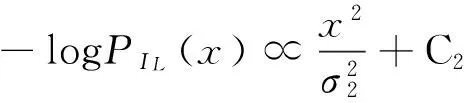
(10)

式中，C1和C2分别为常数。为了使-logPIR(x)与-logPIL(x)具有相同的形式，将-logPIR(x)简化成一个稀疏函数[17]：

ρ(x)=min{x2/k,1}，

(11)

式中,k=10-4。

假设入射分量和反射分量相互独立，采用一阶和二阶滤波器对图像进行梯度滤波，滤波后的输出也相互独立，则：

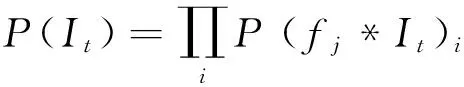
(12)

式中，t∈{R,L}，*表示卷积运算，i代表每一个像素的索引值，fj表示不同的滤波器。其中，一阶滤波器为：

f1=[-1,1],f2=[-1,1]T，

(13)

它们主要用于恢复反射分量IR的重要边缘。二阶滤波器为：

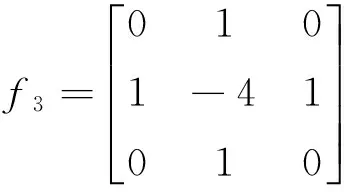
(14)

f3表示拉普拉斯滤波器，主要用于检测入射分量IL的缓慢变化。

结合式(10)、(11)、(12)，可以得到-logP(IR,IL)进行梯度滤波的最小化表达式为：

(15)

将式(6)代入式(15)，可以得到只与IR有关的目标函数：

(16)

其中，为了书写方便，将fj*It缩写成FijIt形式，(IR)i∈[lbi,ubi]是反射分量IR的取值范围，λ是用来控制入射分量IL的平滑度。当λ取值较小时，反射分量中的很多细节被错误地分解到入射分量中，而λ取值较大时，入射分量的部分细节也会出现在反射分量中。因此，本文中λ的取值为50。

式(16)是非凸函数，为了能够快速收敛且正确地将反射分量IR分离出来，需要对上述的目标函数进行了优化。通过采用交替最小化算法[18-19]解决目标函数的非凸性，然后引入一个辅助变量gij将不可微分项FijIR从ρ(·)函数中提取出来，得到一个新的代价函数：

(17)

式中，β是一个加权系数，随着β→∞，式(17)与式(16)等价，本文中β取值范围为β∈(20,40)。利用不同合适的β值进行迭代交替更新gij并计算IR的值，从而使式(17)取得最小值。

固定IR值，gij的更新操作为：

(18)

固定gij值，式(17)是关于IR的一元二次方程，利用二维快速傅里叶变换(2D FFT)计算IR值,即：

(19)

其中，＊表示复数共轭，分母中τ=10-16是为了增加算法的鲁棒性。F表示傅里叶变换，F-1表示傅里叶反变换。

通过公式(19)得到反射分量的取值，但这些值不一定都能落入有效区间[lbi,ubi]内，因此，需要一个合适的常量t对反射分量的取值进行规范化。t值可通过对下面的目标函数的最小化操作来获取，即：

(20)

(21)

由(20)式可以得到t的值，然后利用IR+t代替原来的IR值，得到最终的反射分量图像。经过滤波后的图像比较暗，所以本文采用伽马校正提升反射分量的亮度。

3 结果与分析

本文所采用的实验平台：硬件为Intel(R) Core(TM) i5 CPU，主频3.2 GHz，内存8 G；软件为MATLABR 2014b，Windows 7 操作系统。

3.1 图像去雾算法的主观评价

图3为本文算法的去雾效果图。分别对有雾图像和去雾后的图像选取相对应的两处局部区域进行放大对比，如图4(c)所示。由此可以看出，经过本文算法处理后的图像的对比度得到了较大的提升，图像更加清晰自然。

(a) 有雾图像 (b) 去雾后的图像 (c) 去雾前后局部放大对比

图4 本文去雾算法的效果图

Fig.4 Effect of this article defogging algorithm

为了进一步验证本算法的有效性，分别给出在带色彩恢复多尺度Retinex算法(MSRCR)和基于暗通道先验去雾算法(He算法)[20]以及本文算法的3组图像去雾效果对比图，如图5所示。

从图5可以看出，3种去雾算法都能够使有雾图像的对比度得到不同程度的增强。MSRCR算法处理后的图像整体偏亮，图像近景可以得到较好的增强效果，但远景或者雾浓度较大区域的去雾效果不理想；暗通道先验算法处理后的图像整体偏暗，并且出现了色彩偏移现象；本文算法处理后的图像在细节和色彩方面都得到较好的恢复。

图5 3种去雾算法的效果对比

3.2 图像去雾算法的客观评价

本研究采用信息熵、空间频率、平均梯度以及去雾处理时间这四项指标对上述处理的图像进行客观分析。信息熵反映了图像包含的信息量，信息熵越大则质量越好；空间频率表征一幅图像空间的变化量，空间频率越大则图像越清晰；平均梯度反映了图像细节的平均变化率，平均梯度越大则图像细节信息越突出；去雾处理的时间越小，则表明算法的复杂度越低。表1表示图5中3种去雾算法的客观评价指标。

从表1可以看出，本文算法在信息熵、空间频率和平均梯度三个方面基本高于另外两种算法。在处理时间上，MSRCR算法处理速度最快，其次是本文的算法，最后是暗通道先验算法。

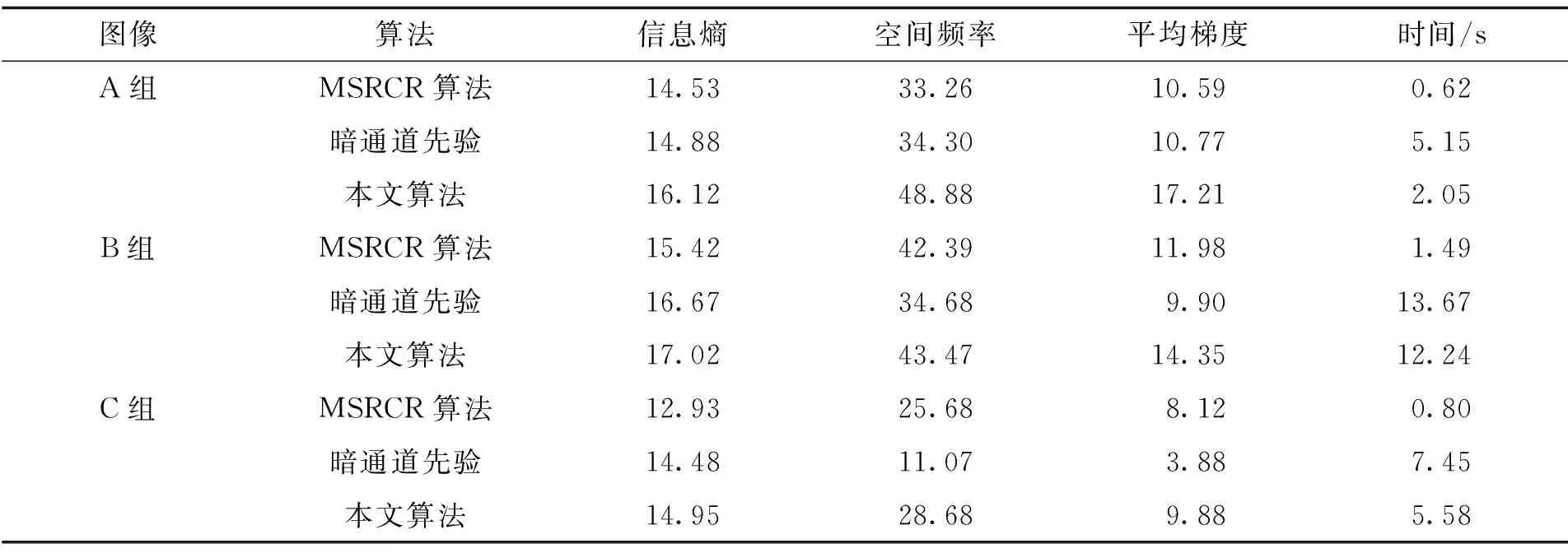
表1 3种去雾算法对图5的客观评价指标对比

4 结 语

本研究在CLAHE算法的基础上，结合图像分解算法较好地恢复了图像的细节和色彩信息，使图像具有良好的视觉效果。本文算法仍具有不足之处在于处理去雾的时间较长且部分图像处理后出现一定的偏色现象，比如图5中本文算法的A组图。接下来的工作是进一步将图像恢复得更自然，同时能够满足实时性要求。

[1] 禹晶,李大鹏,廖庆敏.基于物理模型的快速单幅图像去雾方法[J]. 自动化学报, 2011, 37(2):143-149.

[2] 张冰冰,戴声奎,孙万源.基于暗原色先验模型的快速去雾算法[J]. 中国图象图形学报, 2013, 18(2): 184-188.

[3] 蒋建国,侯天峰,齐美彬.改进的基于暗原色先验的图像去雾算法[J]. 电路与系统学报, 2011, 16(2):6-11.

[4] 蔡超峰,任景英.基于直方图均衡化的手背静脉图像对比度增强[J]. 计算机应用, 2013, 33(4):1125-1127.

[5] 叶松,赵文昌.基于直方图均衡化的图像增强技术分析与Matlab实现[J]. 数字技术与应用, 2012(1):174-174.

[6] 刘德全,崔涛,杨雅宁.局部对比度自适应直方图均衡化图像增强的算法研究[J]. 信息与电脑, 2016(7):79-80.

[7] 杨卫中,徐银丽,乔曦,等.基于对比度受限直方图均衡化的水下海参图像增强方法[J]. 农业工程学报, 2016，32(6):197-203.

[8] 杨骥,杨亚东,梅雪,等.基于改进的限制对比度自适应直方图的视频快速去雾算法[J]. 计算机工程与设计, 2015, 36(1):221-226.

[9] 林笑君,梁凤梅.基于Retinex的一种图像去雾算法[J]. 电视技术, 2013, 37(17):155-158.

[10]肖胜笔,李燕.具有颜色保真性的快速多尺度Retinex去雾算法[J]. 计算机工程与应用, 2015, 51(6):176-180.

[11]JIANG B, WOODELL G A, JOBSON D J.Novel multi-scale retinex with color restoration on graphics processing unit[J]. Journal of Real-Time Image Processing, 2015, 10(2):239-253.

[12]LI S, YEO C, HUA B S.Intrinsic image decomposition using a sparse representation of reflectance[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(12):2904-2915.

[13]刘轩,刘佳宾.基于对比度受限自适应直方图均衡的乳腺图像增强[J]. 计算机工程与应用, 2008, 44(10):173-175.

[14]钟仡龙.单幅图像去雾处理算法研究及软件实现[D]. 成都：西南交通大学, 2012.

[15]阮秋琦.数字图像处理[M]. 北京：电子工业出版社，2011:72-76.

[16]LI Y, BROWN M S.Single image layer separation using relative smoothness[C]//Proceedings of the IEEE conference on computer vision and pattern recognition.Columbus,USA: IEEE,2014: 2752-2759.

[17]LI X, ZHENG S, JIA J.Unnatural L0 sparse representation for natural image deblurring[C]//Proceedings of the IEEE conference on computer vision & pattern recognition.Portland,USA: IEEE,2013:1107-1114.

[18]GEMAN D, YANG C.Nonlinear image recovery with half-quadratic regularization[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 1995, 4(7):932-46.

[19]WANG Y, YANG J, YIN W, et al.A New alternating minimization algorithm for total variation image reconstruction[J]. Siam Journal on Imaging Sciences, 2008, 1(3):248-272.

[20]HE K, SUN J, TANG X.Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2341-2353.

(责任编辑 裴润梅)

Single image dehazing method based on CLAHE and image decomposition

LI Xiu-yu, SONG Shu-xiang, XIA Hai-ying

(College of Electronic Engineering, Guangxi Normal University, Guilin 541004, China)

To solve the problems of low contrast, fuzzy and dim color of the images under haze conditions, a new method based on CLAHE and image decomposition is proposed. At first, the foggy image is enhanced by limiting the contrast histogram equalization. Then based on the illumination-reflection model, several gradient filters are used for the enhanced image through the different features between illumination component and reflection component. And the image is decomposed to obtain the reflection image which contains all the details of the image. Finally, a Gamma transform is used for improving the brightness of the reflection component，and get the final fog eliminated image. At the same time, the information entropy, spatial frequency, average gradient and operation time of the objective evaluation criteria are compared with the multi-scale Retinex color restoration algorithm and the dark channel prior to fog eliminating algorithm. The subjective evaluation and objective evaluation of the experimental results show that this method is better than the MSRCR algorithm and He’s algorithm in the fog image enhancement and color retention.

image defogging; limited contrast histogram equalization (CLAHE); image decomposition; reflection component; image restoration

2016-05-17；

2016-06-27

国家星火计划重点项目(2015GA790002)； 广西自然科学基金资助项目(2013GXNSFBA019278)

宋树祥(1970—)，男，湖南双峰人，广西师范大学教授；E-mail: songshuxiang@mailbox.gxnu.edu.cn。

黎秀玉，宋树祥，夏海英.基于CLAHE和图像分解的去雾方法[J].广西大学学报(自然科学版)，2016，41(5)：1552-1559.

10.13624/j.cnki.issn.1001-7445.2016.1552

TP391

A

1001-7445(2016)05-1552-08