大曲率主管的圆钢管X型节点轴压承载力研究
陈 誉,胡 康,王潮阳,康 琼,陈 千,雷 鸣
(1.长江大学城市建设学院, 湖北荆州434023; 2.华侨大学土木工程学院,福建厦门361021;3.长江大学计算机科学学院, 湖北荆州434023)
大曲率主管的圆钢管X型节点轴压承载力研究
陈 誉1,胡 康1,王潮阳2,康 琼3,陈 千1,雷 鸣1
(1.长江大学城市建设学院, 湖北荆州434023; 2.华侨大学土木工程学院,福建厦门361021;3.长江大学计算机科学学院, 湖北荆州434023)
为研究大曲率主管的圆钢管X型节点轴压性能,采用数值模拟方法对96个不同支、主管外径比β、主管径厚比2γ和主管曲率半径R的圆钢管节点进行有限元参数分析。有限元参数分析结果表明:支、主管外径比β对节点的破坏模式影响较大;曲率半径R对节点破坏模式影响较小。小β值节点主管出现局部凹陷之后产生一定薄膜效应导致承载力出现一定回升;大β值节点试件主管仅出现椭圆化变形无承载力回升现象。当β=0.8时,随着曲率变化节点极限承载力变化较小。当β=0.2、0.4和0.6时,主管曲率半径大于12倍主管直径时,极限承载力变化较小;主管曲率半径小于12倍主管直径时,极限承载力随曲率增大而有所提高。对于相同的主管径厚比2γ,主管曲率半径大于12倍主管直径时,极限承载力变化较小;主管曲率半径小于12倍主管直径时,极限承载力随曲率增大而有所提高。在欧洲钢结构规范(Eurocode3 Design of Steel Structures)中的主管平直的圆钢管X 型节点极限承载力计算公式的基础上,采用乘以修正系数的方式拟合出大曲率主管的圆钢管X型节点轴压承载力计算公式,为该类节点的设计提供参考。
圆钢管X型节点;大曲率主管;轴压;承载力;计算公式
0 引 言
目前大曲率主管的桁架结构越来越广泛的应用在大跨度结构中。Qian等[1]提出一种新的荷载—变形公式来计算X型和K型的空心钢管节点。强度参数遵循国际焊接协会的最新要求,而几何参数来源于圆形X型和K型管节点的有限元模型。提出的荷载变形公式与实验所得的平面内X型和K型节点的结果能够很好的吻合。无量纲的荷载变形公式为目前计算空间钢框架结构提供了深入的分析方法。Zhu等[2]研究了圆钢管T型外加强节点受力性能。节点强度随着加强板的尺寸的增加而显著增加。加强的效果更加依赖于加强板的长度而不是高度,但是在工程中可以采用等边长的加强板更为实际。Wang等[3]进行了系统试验调查轴向荷载作用下圆支管和方主管的X型管节点。对5个非刚性的和3个刚性节点在单调加载条件下的焊接钢管节点进行了测试。分析了节点的应变分布、失效模式和焊缝的强度。结果表明,非均匀应变分布存在于非刚性的节点而刚性节点的应变分布较为均匀。非刚性的节点的焊缝强度明显比刚性的节点小。最后根据有效长度的方法提出轴向荷载下焊缝强度公式。Xu等[4]研究了在轴向载荷作用下的薄壁圆钢管混凝土T、Y、K和KT节点的应力集中系数。试验探讨了热点应力沿着主管和支管的分布。在11根试验管节点的主管中填充了混凝土。测试结果表明,应力分布主要是由节点类型决定,而主管的壁厚影响不大。由试验获得的应力集中系数与欧洲钢结构规范公式中计算管节点的应力集中系数较吻合。Chen等[5]通过参数有限元研究揭示圆钢管(CHS) 节点的失效模式和塑性分布规律。其承载力计算公式是基于欧洲钢结构规范的前提下提出了利用多元线性回归对圆形支管-H型主管的T型管节点受轴向荷载作用的。目前采用欧洲规范来预测圆形支管-H型主管的T型管节点是不安全的。节点的强度计算采用所提出的公式与有限元分析所得到的结果较接近,这意味着该设计方程证实是准确的。Zhu等[6]针对加强的和未加强的圆钢管节点进行了在轴向荷载作用下的对比极限承载力试验。采用了3组共6个试件,试件的支管与主管的直径比分别为0.26,0.51和0.74,然后通过试验确定响应的极限承载力。对样本参数、实验装置和测试结果都进行了描述。且对无加强和加强T型节点的失效模式进行了比较。无加强节点失效模式是由于主管塑性作用,而加强节点失效模式是由于主管的屈曲。实验表明,T型管节点的外部加劲环的轴向抗压强度显著增加。每个加强节点受力表现得像一个在跨中施加在支管上集中荷载的梁。加强节点的强度可以通过冠点的塑性弯矩得到。目前国内外学者的研究重点在小曲率或者平直主管的圆钢管节点静力和滞回性能,针对大曲率主管的圆钢管节点极限承载力研究较少。
本文采用非线性有限元数值模拟方法,基于课题组前期大曲率主管的圆钢管X型节点轴压试验研究成果[7],通过对比试验结果和参数模拟结果,为大曲率主管的X型圆钢管节点轴压性能的参数分析找出合理的有限元计算模型,并为试验提供补充,以深入研究主管曲率等参数对大曲率主管X型圆钢管节点轴压极限承载力的影响,最终提出该类节点在轴压力作用下的极限承载力计算公式。
1 有限元模型

图1 节点网格划分图Fig.1 Mesh of joints
ABAQUS是目前国际上最优秀的非线性有限元分析软件之一。本文采用ABAQUS6.11有限元软件对试验大曲率主管的圆钢管节点进行有限元模拟分析[8]。试件边界条件均为:底板约束UX、UY、UZ、RX、RY、RZ六个自由度,加载板约束RX、RY、RZ三个自由度,采用UX、UY、UZ位移加载方式,按试件偏心距及试验整体位移确定UX、UY、UZ值。本试验有限元模拟采用ABAQUS弹塑性实体单元(C3D8I)来模拟[9]。钢材的本构由材性试验得到,材料服从Von-Mises屈服准则[10]。
大曲率主管的圆钢管节点网格划分如图1所示。由于空钢管节点计算时间较短,网格划分较密以保证计算精度,支管与主管交汇区域与非交汇区域网格粗细程度不同。
2 有限元试验模拟结果
2.1 破坏模式
如图2所示,大曲率主管的X型圆钢管节点在轴压极限荷载作用下的试验与有限元模拟破坏模式较为一致,均为主管塑性的破坏模式。随着曲率的变化,主管塑性发展程度与范围有所不同。在曲率最大情况下可能会发生支管根本的局部屈曲。

(a) X9×2.5试验图

(b) X9×2.5试件模拟图

(c) XB114×3.0R420试验图
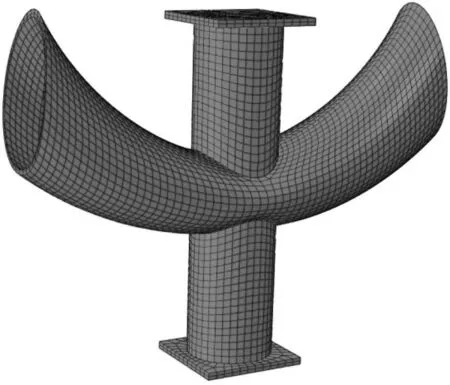
(d) XB114×3.0R420试件模拟图
2.2 荷载—整体位移曲线
图3为试验和有限元模拟的荷载—整体竖向位移曲线比较。由图3可以看出:有限元模拟的曲线和试验曲线较为吻合,各试件的有限元模拟曲线的初始刚度都稍大于试验曲线的初始刚度。

(a) X9×2.5R840
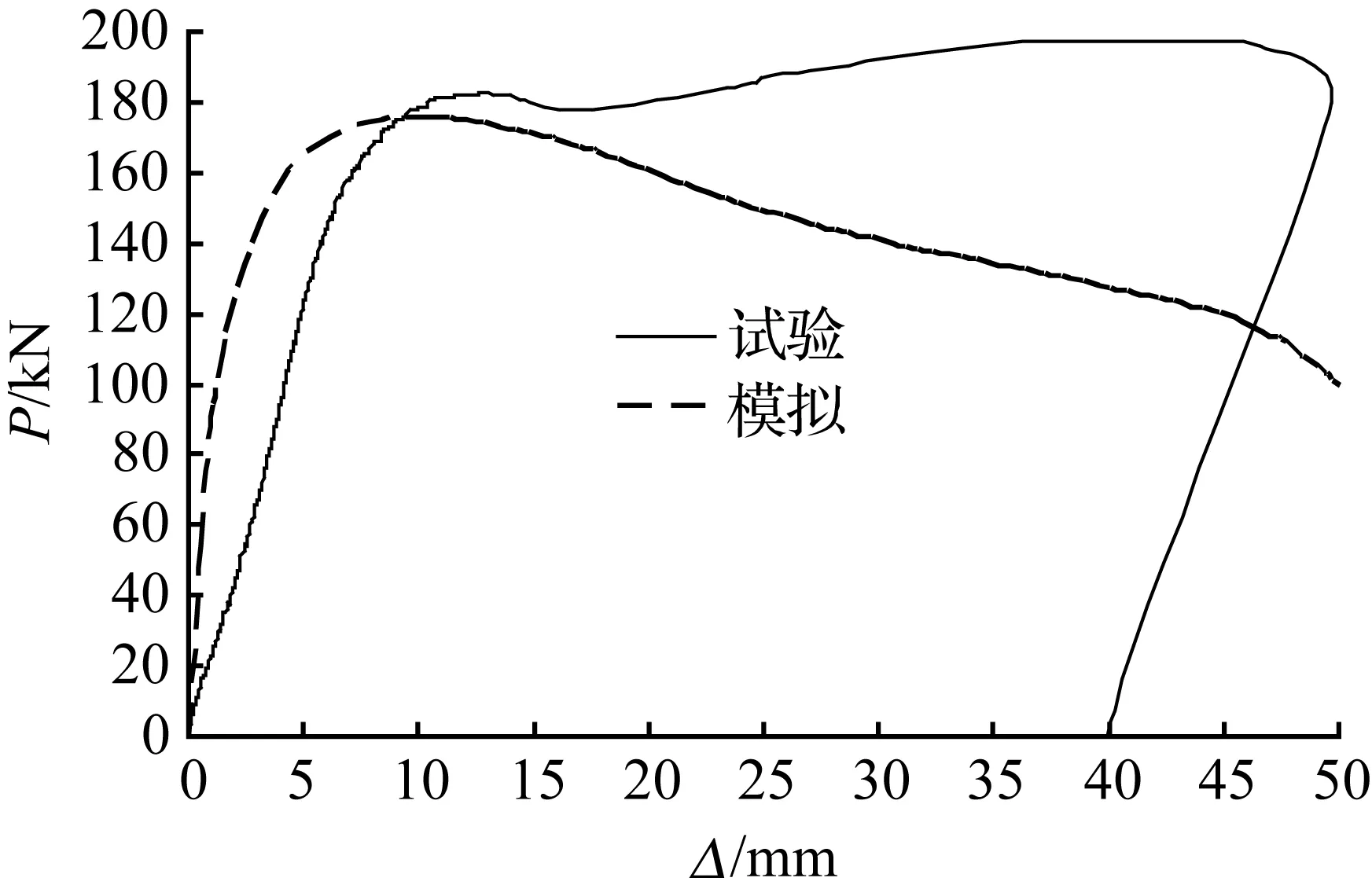
(b) XB114×3.0R1260
图3 荷载—整体位移曲线比较图
Fig.3 Comparison of load-displacement curves between test and FEA
2.3 极限承载力有限元计算结果
表1给出了有限元模拟和试验的极限承载力误差分析表。从表1中可以看出,数值模拟的极限承载力和试验极限承载力较为接近,最大误差正10.0%,最小负误差-10.5%,误差均在可以接受的范围。产生误差的原因可能是试验加载偏心、焊缝残余应力和材料的初始缺陷等。

表1 节点模拟极限承载力和试验值比较
3 有限元参数研究
3.1 计算模型
本文主要研究主管曲率和几何参数对大曲率主管的X型圆钢管节点轴压承载力和破坏模式的影响。研究的几何参数包括支主管外径比β=d1/d0(d1、d0分别为支管和主管直径)和主管径厚比2γ=d0/t0(d0、t0分别为主管的直径和壁厚),每个参数各变化4组。本次参数分析未研究支主管壁厚比值τ=t1/t0(t0、t1分别为主管和支管的壁厚)变化对节点轴压性能的影响,主要考虑节点真正的极限承载力为节点的主管径向轴压承载力,理想破坏模式为主管塑性破坏而支管不发生破坏,设置τ=0.8是为了保证支管不先于主管发生破坏,该参数变化引起的试件极限承载力变化主要为τ较小时支管发生破坏,该破坏模式下的承载力不是节点的最大极限承载力,所以本参数分析未变化支、主管壁厚比值τ;主管曲率半径R变化6组,共96个节点。β值取为0.2,0.4,0.6和0.8;2γ值取为30,40,50和60,R/d0值取为3,6,9,12,20和∞。
3.2 有限元计算结果
一般情况下,相贯线鞍点附近区域及主管侧壁中心首先进入塑性,之后塑性区由主管中心向两边扩展。β值越大,扩展范围越广,主管横截面45°区域应力较小,如图4所示。破坏模式均为主管塑性:小β值试件主管出现局部凹陷,之后产生一定薄膜效应导致承载力出现一定回升;大β值试件主管出现椭圆化变形无回升现象,如图5所示。

(a) 加载初期

(b) 加载中期

(c) 加载后期
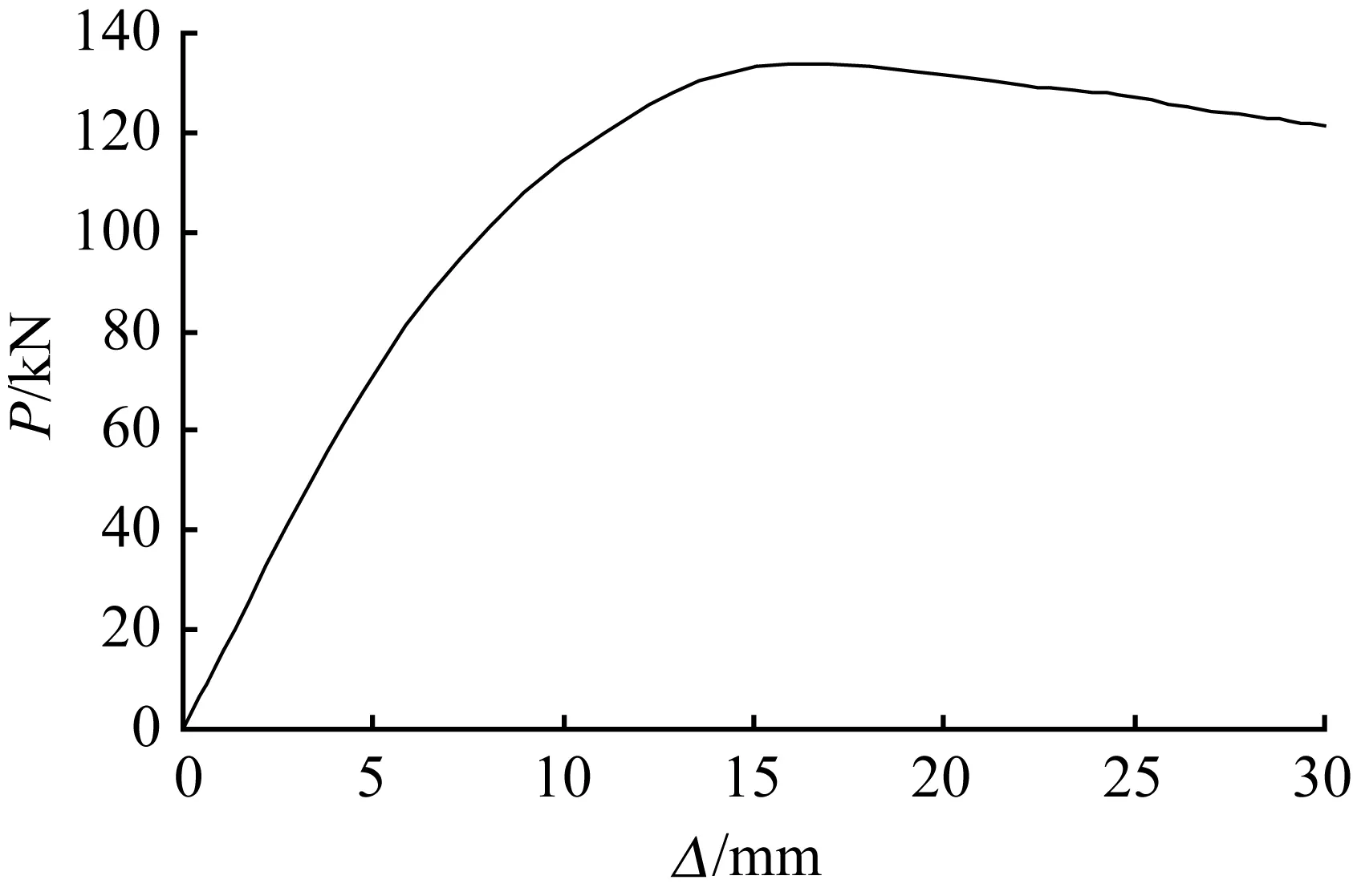
所有节点具有较高的延性,小β值(β=0.2)试件主管出现局部凹陷,导致荷载突然下降,之后产生一定薄膜效应导致荷载出现一定回升,典型节点的荷载—位移曲线如图5所示。小β值节点随着主管从平直到弯曲荷载—位移曲线特性发生改变:有出现一次极值到出现两次极值然后达到破坏。大β值(β>0.2)节点随着主管从平直到弯曲荷载—位移曲线特性没有发生根本改变。
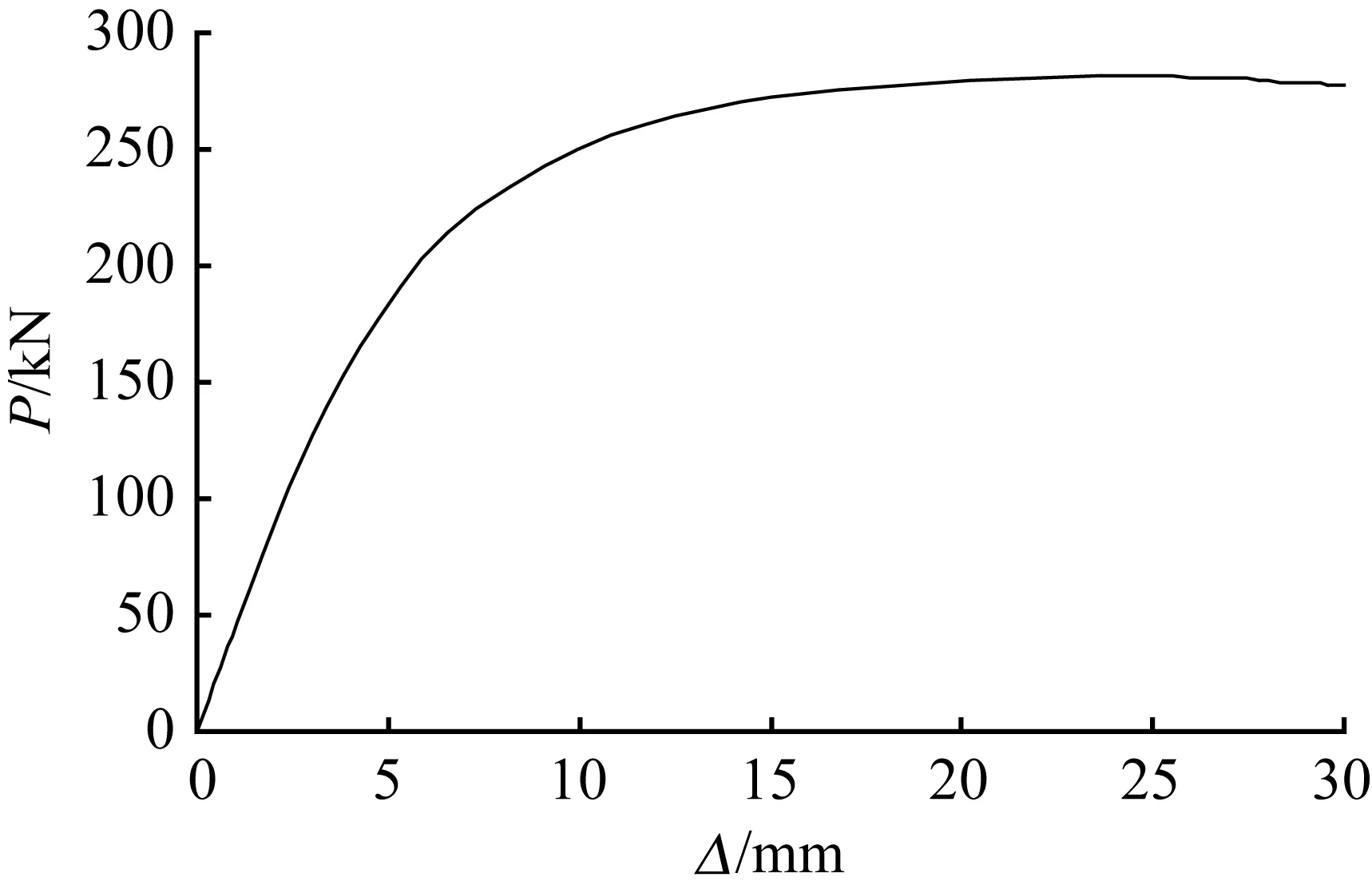
(a) 2γ=40,β=0.6,R=900
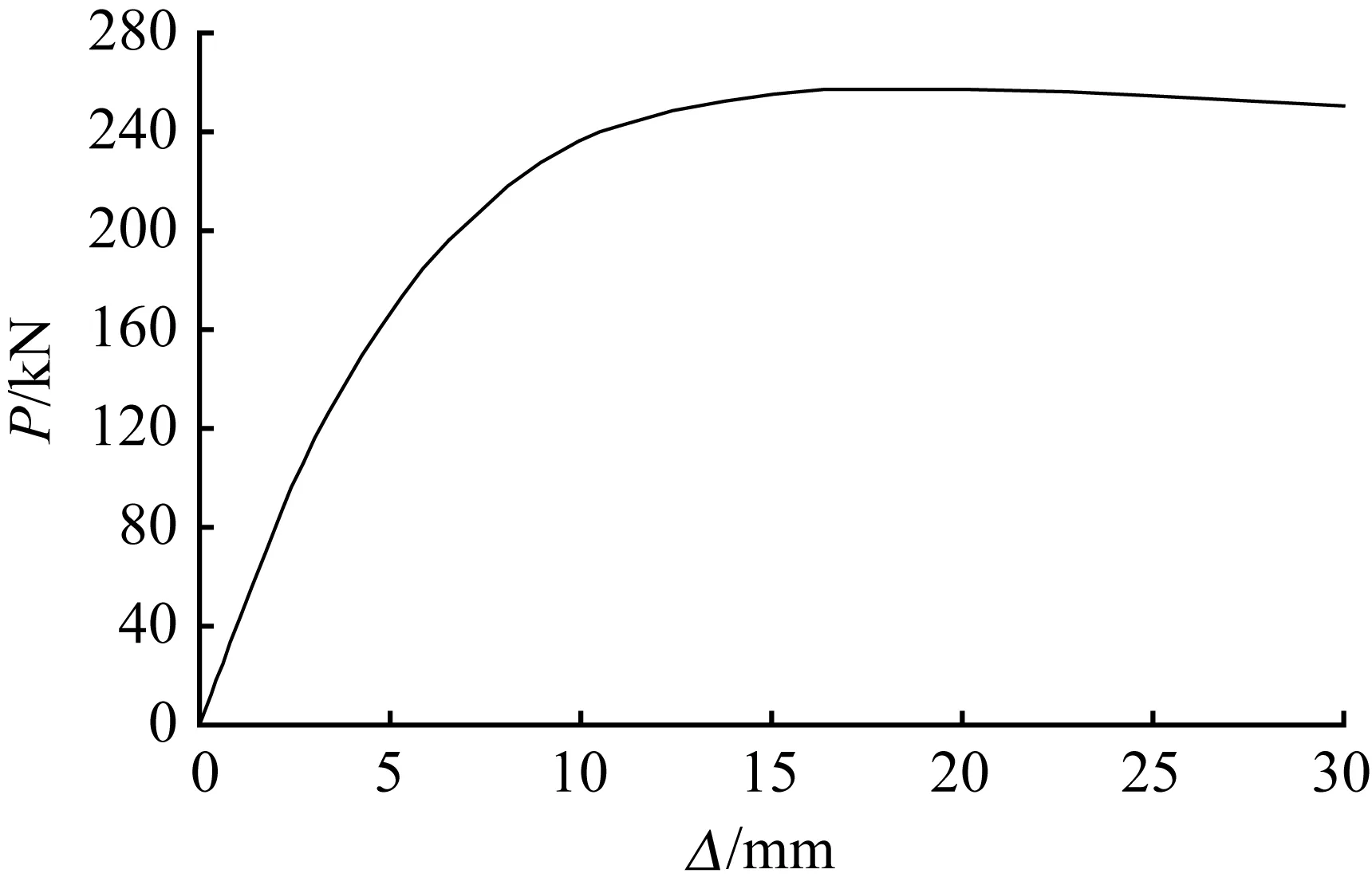
(b) 2γ=40,β=0.6,R=∞

(c) 2γ=40,β=0.2,R=900
(d) 2γ=40,β=0.2,R=∞
图5 典型试件荷载—整体位移曲线
Fig.5 Load-displacement curves of typical joints
图6和图7分别为相同主管径厚比2γ=d0/t0和支主管外径比β=d1/d0条件下节点极限承载力关于曲率的变化曲线。显然,支、主管外径比β越大,主管径厚比2γ越小,节点的极限承载力越大。对于相同的主管径厚比2γ,曲率小于1/3 600 mm(主管曲率半径大于12倍主管直径)时,极限承载力变化较小,曲率大于1/3 600 mm(主管曲率半径小于12倍主管直径)时,极限承载力随曲率增大而有所提高。对于相同的支主管外径比β=0.2、0.4和0.6,曲率小于1/3 600 mm(主管曲率半径大于12倍主管直径)时,极限承载力变化较小,曲率大于1/3 600 mm(主管曲率半径小于12倍主管直径)时,极限承载力随曲率增大而有所提高。β越小,提高幅度越大。对于相同的支主管外径比β=0.8,极限承载力变化较小。

(a) 2γ=30

(b) 2γ=40

(c) 2γ=50

(d) 2γ=60
图6 相同2γ的节点承载力—曲率变化曲线
Fig.6 Ultimate capacity-curvature curves of joints with same 2γ

(a)β=0.2
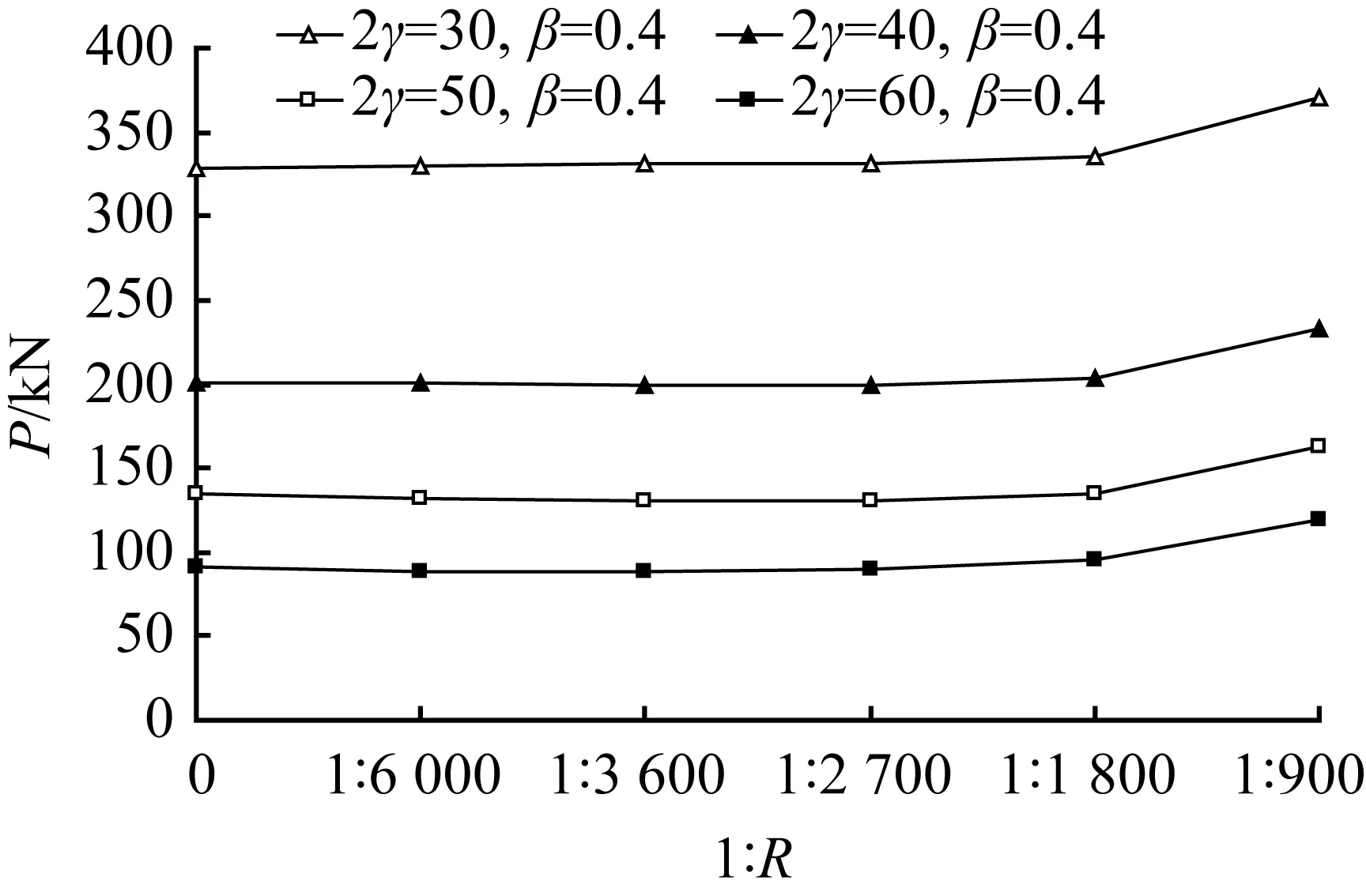
(b) β=0.4

(c)β=0.6
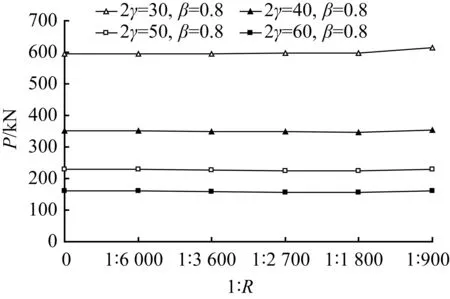
(d) β=0.8
图7 相同β的节点承载力—曲率变化曲线
Fig.7 Ultimate capacity-curvature curves of joints with sameβ
4 极限承载力计算公式
本文拟在主管平直的空心圆钢管节点轴压极限承载力的基础上乘以调整系数ΨX得到大曲率主管的CHS轴压节点极限承载力[11-12]。欧洲钢结构规范(Eurocode3 Design of Steel Structures)对于主管平直的空心圆钢管相贯节点的极限承载力计算公式为:

(1)
其中:fy0为主管钢材屈服强度;t0为主管管壁厚度;β为支主管外径比;kp为主管轴向应力影响系数,取1.0。
根据主管弯曲程度,调整系数ΨX如下:
当R/d0≤12时,
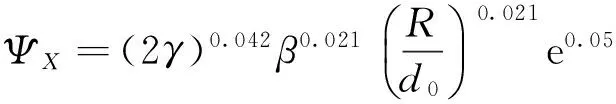
(2)
当R/d0>12时,
ΨX=1.0,
(3)
所得的大曲率主管的X型空心圆钢管节点轴压承载力计算公式为:
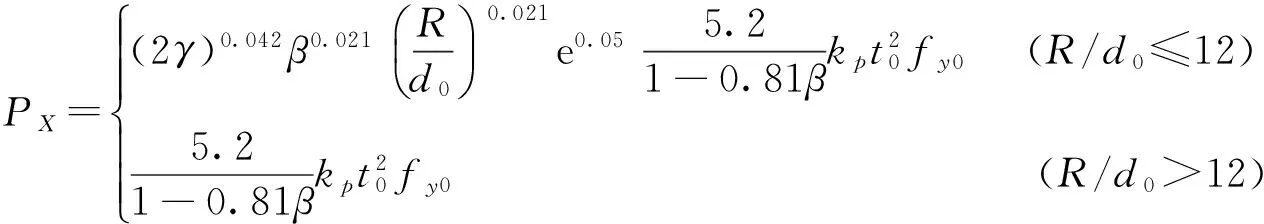
(4)
其中:d0为主管外径;t0为主管壁厚;2γ为主管径厚比d0/t0;β为支主管外径比;R为主管曲率半径;e为常数,e=2.718 28;kp为主管轴向应力影响系数,取1.0;fy0为主管钢材屈服强度。
有限元计算值与按公式(4)计算所得的计算值对比见图8。由图8可知,有限元计算值与修正后的公式计算值的比值大多集中在0.9~1.0和1.0~1.1,最大值为1.39,最小值为0.81,平均值为1.06。修正后的公式离散性较小,与有限元计算值比较接近,均值达到1.06,故精度较高,且有一定安全性。

(a) 单个有限元模型的比值分布
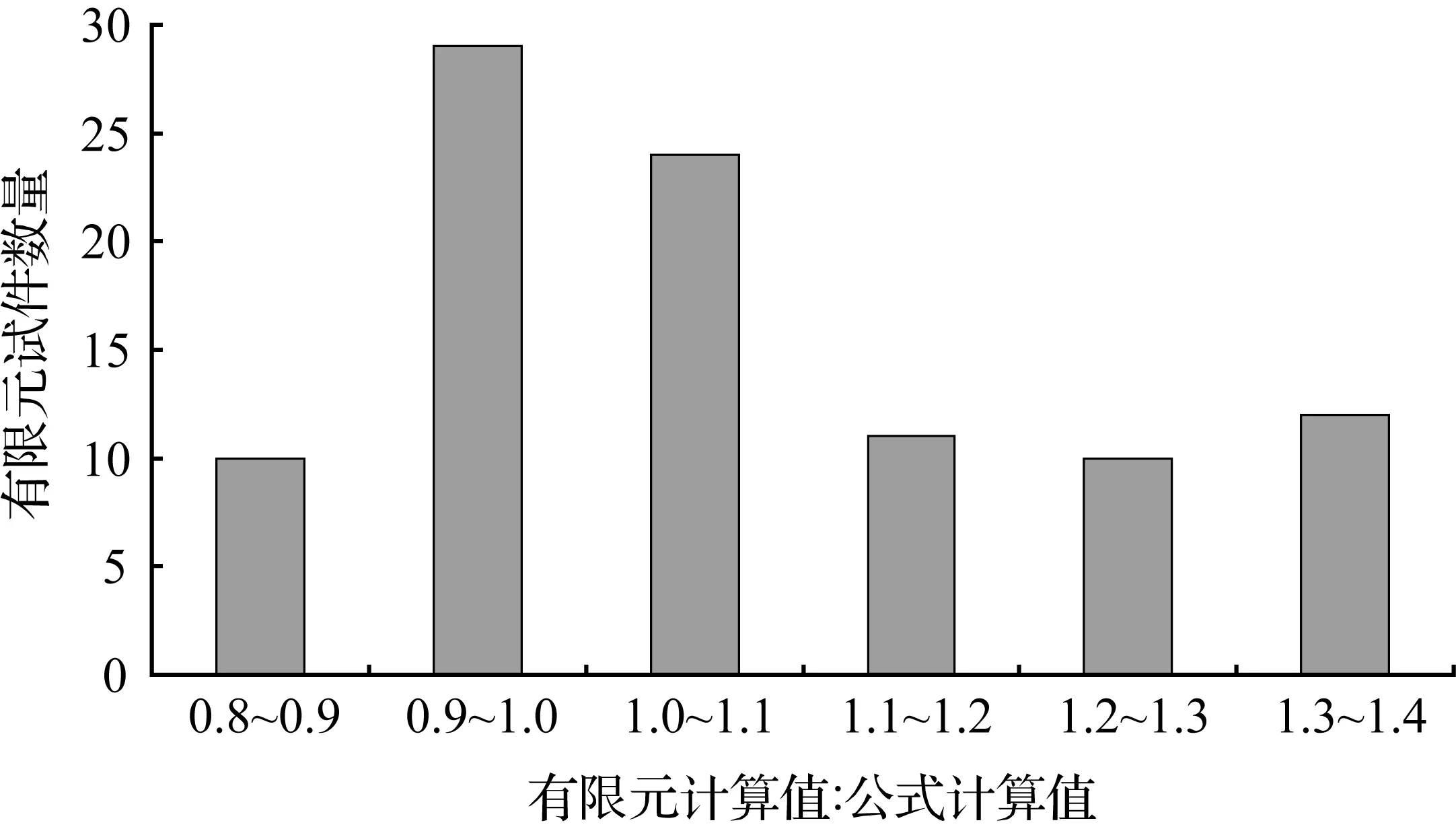
(b) 所有有限元模型的比值分布
5 结 论
①小β值(β=0.2)试件主管出现局部凹陷之后,产生一定薄膜效应,导致承载力出现一定回升;大β值(β>0.2)试件主管仅出现椭圆化变形无回升现象。
②对于相同的支、主管外径比β=0.8时,随着曲率变化节点极限承载力变化较小。在β=0.2、0.4和0.6时,主管曲率半径大于12倍主管直径时,极限承载力变化较小;主管曲率半径小于12倍主管直径时,极限承载力随曲率增大而有所提高。
③对于相同的主管径厚比2γ,主管曲率半径大于12倍主管直径时,极限承载力变化较小;主管曲率半径小于12倍主管直径时,极限承载力随曲率增大而有所提高。
④本文提出的大曲率主管的圆钢管X型节点的轴压极限承载力公式由于有限元计算值与修正后的公式计算值的平均值达到1.06,故精度较高,并具有一定安全性。
[1] QIAN X D, ZHANG Y, CHOO Y S.A load-deformation formulation for CHS X- and K-joints in push-over analyses[J]. Journal of Constructional Steel Research, 2013, 90(3):108-119.
[2] ZHU L, ZHAO Y, LI S W, et al. Numerical analysis of the axial strength of CHS T-joints reinforced with external stiffeners[J]. Thin-Walled Structures, 2014, 85(8):481-488.
[3] WANG W, GU Q, MA X X, et al. Axial tensile behavior and strength of welds for CHS branches to SHS chord joints[J]. Journal of Constructional Steel Research, 2015, 115(6):303-315.
[4] XU F, CHEN J, JIN W L.Experimental investigation of SCF distribution for thin-walled concrete-filled CHS joints under axial tension loading[J]. Thin-Walled Structures, 2015, 93(9):149-157.
[5] CHEN Y, FENG R, WEI L.Design of CHS brace-to-H-shaped chord T-joints under axial compression[J]. Thin-Walled Structures, 2016, 98(4):274-284.
[6] ZHU L, HAN S, SONG Q M, et al. Experimental study of the axial compressive strength of CHS T-joints reinforced with external stiffening rings[J]. Thin-Walled Structures, 2016, 98(3):245-251.
[7] CHEN Y, FENG R, WANG C Y.Tests of steel and composite CHS X-joints with curved chord under axial compression[J]. Engineering Structures, 2015, 99(3):423-438.
[8] FENG R, YOUNG B.Experimental investigation of cold-formed stainless steel tubular T-joints[J]. Thin-walled Structures, 2008, 46(10): 1129-1142.
[9] SHAO Y B, LI T, LIE S T.Hysteretic behavior of square tubular T-joints with chord reinforcement under axial cyclic loading[J]. Journal of Constructional Steel Research, 2011, 67(1): 140-149.
[10]胡康,杨简,雷鸣,等.平面内弯矩作用下主圆支方K型节点的应力集中系数研究[J]. 广西大学学报(自然科学版),2016,41(3):626-634.
[11]陈希湘,冯然,陈誉,等.天然气管道悬索跨越结构风致响应研究[J]. 广西大学学报(自然科学版),2015,40(2):317-324.
[12]陈希湘,陈誉,林智寰.普光天然气管道悬索桥地震时程反应研究[J]. 广西大学学报(自然科学版),2014,39(6):1432-1440.
(责任编辑 唐汉民 梁 健)
Research on ultimate bearing capacity of CHS X-joints with large curvature chord under axial compression
CHEN Yu1, HU Kang1, WANG Chao-yang2, KANG Qiong3, CHEN Qian1, LEI Ming1
(1.School of Urban Construction, Yangtze University, Jingzhou 434023, China;2.College of Civil Engineering, Huaqiao University, Xiamen 361021, China;3.College of Computer Science, Yangtze University, Jingzhou 434023, China)
In order to research the mechanical behaviors of X-joints with circular hollow section (CHS) and large curvature chord under axial compression, ninety-six CHS X-joints with different brace to chord diameter ratioβ, chord diameter to thickness ratio 2γand chord curvatureRwere studied by the finite element method. The results of finite element (FE) parametric analysis indicated that brace to chord diameter ratioβhas relatively large effect on the failure mode, and that chord curvature has relatively small effect on the failure mode. Because membrane effect appears after surface plasticity of chord, the bearing capacity of joints with smallβincreases slowly; ovalization just appears in joints with largeβ. Whenβ=0.8, the effect of curvature on the ultimate bearing capacity of joints is unobvious. When radius of chord curvature is larger than 12 times of chord diameter, the effect of curvature on the ultimate bearing capacity of joints withβof 0.2, 0.4 and 0.6 is unobvious. If radius of chord curvature is smaller than 12 times of chord diameter, the ultimate bearing capacity of joints increases with the increase of curvature. When radius of chord curvature is larger than 12 times of chord diameter, the effect of curvature on the ultimate bearing capacity of joints under the same 2γis unobvious. If radius of chord curvature is smaller than 12 times of chord diameter, the ultimate bearing capacity of joints under the same 2γincreases with the increase of curvature. Based on the design equation of CHS X-joints with straight chord in Eurocode3 Design of Steel Structures, formulae predicting the ultimate bearing capacity of CHS X-joints with large curvature chord were proposed by applying multivariate regression analysis to design the CHS X-joints. Results calculated using the proposed design equations agree well with finite element analysis (FEA) results.
circular hollow section (CHS) X-joints; large curvature chord; axial compression; ultimate capacity; formulae
2016-03-20;
2016-08-08
国家自然科学基金资助项目(51478047,51278209)
陈 誉(1978—),男,湖北公安人,长江大学教授,博士;E-mail:kinkingingin@163.com。
陈誉,胡康,王潮阳,等.大曲率主管的圆钢管X型节点轴压承载力研究[J].广西大学学报(自然科学版),2016,41(5):1321-1329.
10.13624/j.cnki.issn.1001-7445.2016.1321
TU392.3
A
1001-7445(2016)05-1321-09

