基于改进QPSO算法的地铁列车节能优化操纵研究

王合良，贺德强，莫志刚，苗 剑

(1.广西大学机械工程学院， 广西南宁530004; 2.南宁轨道交通集团有限责任公司， 广西南宁530021)



基于改进QPSO算法的地铁列车节能优化操纵研究

王合良1，贺德强1，莫志刚2，苗 剑1

(1.广西大学机械工程学院， 广西南宁530004; 2.南宁轨道交通集团有限责任公司， 广西南宁530021)

地铁列车的节能优化操纵是降低能耗的重要途径。针对地铁列车在不同工况与线路条件下的运行特点，对其进行动力学分析。参照线路纵断面化简原理对线路进行简化，并根据节能优化原则与列车站间运行的约束条件建立实际路况下的能耗模型。引入改进量子粒子群优化算法，将列车运行速度、加速度等参数进行实数编码，通过迭代寻优与变异操作求解列车站间运行的最低能耗，并获取列车最优运行速度及工况转换点等特征参数。通过南宁地铁一号线某站间线路的实例仿真证明，该方法在保证列车舒适性、安全性与准点停靠的前提下，降低列车运行能耗达9.21%。

优化操纵；能耗模型；量子粒子群；迭代寻优

0 引 言

随着城市地铁线路的大规模建设，地铁以其良好的安全性和舒适性，成为公共交通的重要组成部分。地铁列车运行具有站间距离短、线路复杂、频繁牵引与制动等特点，因此在运行过程中会消耗大量能量。如何在保证列车安全平稳运行的前提下，最大限度降低列车运行能耗，成为列车优化操纵领域的重要研究课题。国内外专家学者针对列车节能优化展开了深入研究。唐海川等[1]采用二次规划算法优化追踪列车运行曲线，提高列车再生制动能量利用率，从而降低运行能耗。李波等[2-3]以牵引理论为基础，构建列车节能控制模型，并采用实数遗传算法得出既定线路下的优化操纵曲线。余进等[4]采用多目标微粒群算法求解列车能耗模型，获取多组最优解，可根据实际运行情况选择最佳的控制策略。熊超彬[5]采用萤火虫算法优化操纵工况序列，确定操纵工况的转换点，实现列车节能操纵的离线优化。Hai[6]将列车运行线路离散为5个区段，并采用极大值原理逐段分析列车能耗，得到列车最佳运行曲线。Hwang[7]综合利用模糊聚类与遗传算法，建立列车能耗的模糊控制模型，得到列车运行时间与能耗折衷的运行策略。文献[8]采用遗传算法全局优化列车节时与节能模型，并引入模拟退火算法增强局部寻优能力，求解列车在节时模式与节能模式下的最低能耗。

现有的研究成果均是采用某种节能优化算法求解列车能耗模型，得到相应的优化操纵策略，并取得了良好的节能效果，但大多不能较好地平衡准点运行与降低能耗的关系，且实时性较差。本文采用改进量子粒子群优化算法，将列车运行速度、加速度、距离等参数进行实数编码，通过迭代寻优与变异操作，确定列车工况转换点及最佳匀速速度，最终求得列车定时节能模式下的最低能耗，并绘制优化操纵曲线，同时可以根据运行线路及时刻表的变化为列车节能驾驶提供实时的理论指导。

1 地铁列车模型

地铁列车运行主要包括牵引、惰行和制动三种工况[9]，地铁线路由直道、弯道、坡道以及弯坡道复合线路组成。列车在运行时司机可以根据不同路况、站间距离、速度限制等选择不同的操纵方式。由于地铁线路较为复杂，列车运行过程中需要频繁的牵引和制动，为减少阻力做功，降低运行能耗，需要构建列车的优化控制模型来解决此问题。

1.1 动力学模型

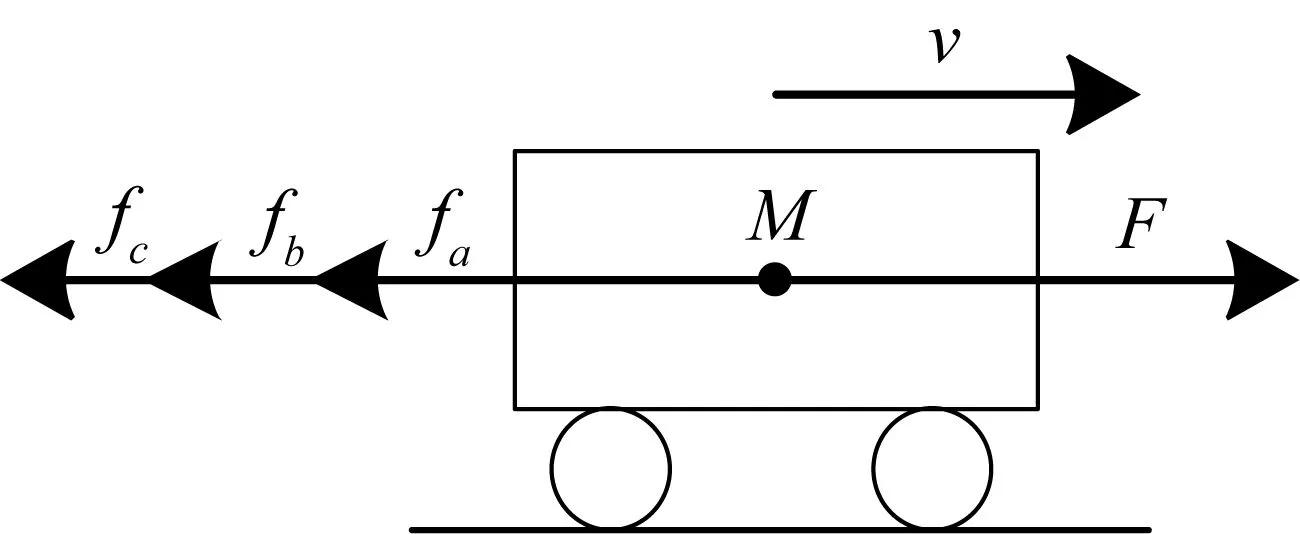
图1 列车动力学模型Fig.1 Dynamic model of train

列车动力学模型如图1所示。

地铁列车运行时，主要受到牵引力、基本阻力、附加阻力(仅考虑坡道阻力与曲线阻力)与制动力的作用[10]。将地铁列车简化为单质点模型，对列车受力分析，得到不同工况下的合力方程为：

(1)

根据牛顿第二定律与运动学公式得：

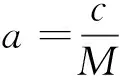
(2)

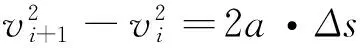
(3)

式(1)～(3)中，F为牵引力(N)，fa为基本阻力(N)，fb为附加阻力(N)，fc为制动力(N)，M为列车质量(kg)，a为列车加速度(m/s2)，vi为i时刻列车运行速度(m/s)，vi+1为i+1时刻列车运行速度(m/s)，Δs为列车单位运行距离(m)。

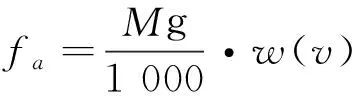
(4)

w(v)=a+bv+cv2，

(5)

式(4)～(5)中，w(v)为单位基本阻力(N/kN)，a，b，c为阻力常数。

fb=fw+fp,

(6)

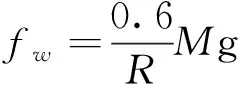
(7)

fp=Mgi,

(8)

式(6)～(8)中，fw为曲线附加阻力(N)，fp为坡道附加阻力(N)，R为弯道半径(m)，g为重力加速度(9.8 m/s2)，i为坡道坡度(‰)。

1.2 线路纵断面化简

由于地铁线路复杂，列车受力情况会因线路参数的影响而发生显著变化。为简化列车运行线路，减少计算量，需对线路纵断面进行化简[11]。

将若干相临、坡度相近的区段简化为一个等效路段，化简路段的长度为各实际区段的长度之和。化简路段的坡度值为：

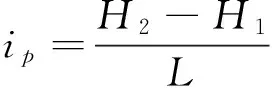
(9)

式中，H1，H2为化简路段起点与终点的高度(m)，L为化简路段总长度(m)。

为减小误差，提高化简精度，化简路段需满足经验公式：

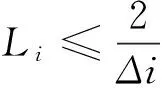
(10)

式中，Li为化简路段中任一实际区段的长度，Δi为化简坡度与化简路段中任一实际坡度的代数差绝对值。

化简线路纵断面后，需将曲线附加阻力(忽略隧道阻力)折算为坡度，曲线折算坡度为：

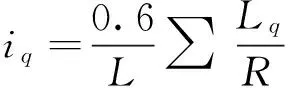
(11)

式中，Lq为弯道长度(m)，R为弯道半径(m)。

线路化简后的加算坡度为：

ij=ip+iq。

(12)

因此，化简后的列车附加阻力可以表示为：

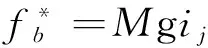
(13)

另外，线路化简前后的列车基本阻力保持不变，如公式(4)所示。

1.3 能耗模型

铁列车能耗模型是典型的多目标、多约束的复杂函数模型，为简化模型求解过程，根据节能优化原则对列车运行做如下假设：

①将线路离散为n个运行区段(离散步长为0.01 m)，各区段内附加阻力值不变，且仅考虑坡道附加阻力和曲线附加阻力。

图2 列车节能模式运行示意图 Fig.2 Schematic of train energy-saving operation

②列车采用最大牵引力启动，达到最大功率时，保持恒功率运行。当列车速度增加到某一目标速度时，保持匀速行驶[12-13]。运行过程中应适度增加惰行时间，避免紧急制动。

③列车制动采用再生制动与空气制动混合制动的方式，优先采用再生制动，当速度降为5 km/h时，采用空气制动。列车节能模式运行示意图如图2所示。

牵引工况下，牵引力克服列车阻力做功，引起动能的变化，由动能定理：

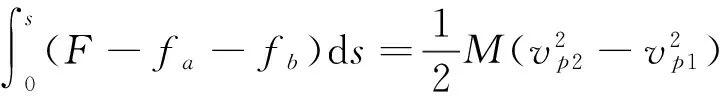
(14)

可得牵引能耗：

(15)

式中，s为某牵引区段运行距离，vp2为牵引末速度，vp1为牵引初速度。

列车在惰行工况下，无牵引力与制动力，仅凭惯性运行，因此能耗忽略不计。

制动工况下，列车再生制动将动能转换为电能并反馈给接触网，供相邻运行的列车使用[14]。

再生制动产生的能量：

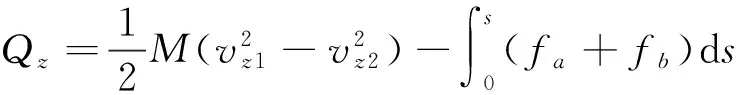
(16)

式中，vz1为制动初速度，vz2为制动末速度。

综上所述，若列车再生能量利用率以50%计算，且在列车运行时刻表已定的情况下，站间运行总能耗的目标函数为：

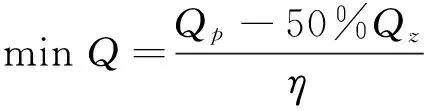
(17)

式中，η为电能利用率，η∈(0,1)。

约束条件为：

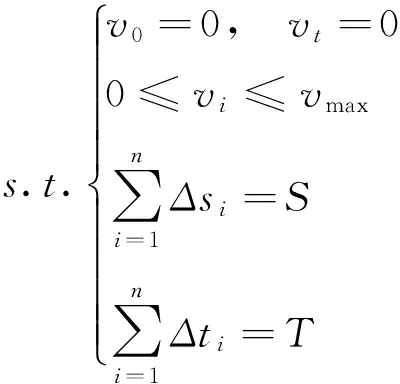
(18)

式中，v0为列车运行初速度，vt为列车运行末速度，vi为列车瞬时速度，vmax为列车限速，S为站间距离，Δti单位区段运行时间，T为站间运行准点时间。

2 改进量子粒子群算法求解能耗模型

量子粒子群优化算法(Quantum Particle Swarm Optimization, QPSO)，将粒子的寻优空间视为量子力学中的势场，全局最优解为势场中势能最低点(势场中心)，寻优过程即为粒子在势场中向势能最低点的移动过程[15]。在QPSO算法中，粒子的运动状态用其波函数Ψ来表示，代替标准粒子群优化算法(PSO)中粒子的速度更新和位置更新方程[16]。由于粒子在量子空间中满足聚集态的性质，可以在整个可行空间中进行搜索。但该算法的最优解精度依赖于势场中心的选取，而且势场中心的构造方法较为单一，导致了种群多样性的丢失。因此应对更新后的粒子进行变异操作，以增加种群的多样性，同时提高算法的收敛速度和精度。

采用改进QPSO算法，将地铁列车能耗模型的求解转化为有约束的函数极值寻优过程。改进QPSO算法求解列车能耗模型的流程为：

①输入地铁列车能耗模型，作为算法寻优的目标方程。

②算法参数的初始化。设定粒子群规模、进化代数、变异概率、势场中心等参数。

③将列车能耗模型中的速度v、加速度a、距离s等参数进行实数编码，分别表示为v∈{v1,v2，…，vn-1,vn}，a∈{a1,a2,…,an-1,an}，s∈{s1,s2,…,sn-1,sn}。以速度、加速度、距离等参数作为搜索粒子，初始化各粒子的数值。

④计算粒子的适应度值。

⑤计算粒子的个体最优解与全局最优解。

⑥更新粒子，并对更新后粒子进行变异操作，以增加种群的多样性。

⑦将每个粒子的适应度值与个体最优解和全局最优解比较，更新全局最优解与个体最优解。

⑧满足中止条件(达到最大迭代次数或最优解无变化)时，输出粒子的最优解。将粒子最优解代入能耗模型，得出最低能耗值及各工况转换点。

改进QPSO算法求解能耗模型的流程如图3所示。

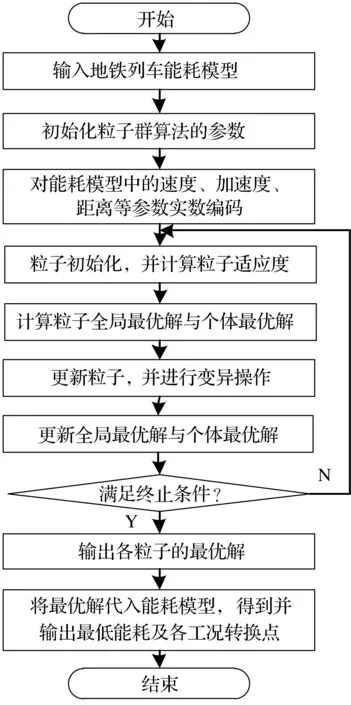
图3 改进QPSO算法流程图

3 实例仿真

本文以南宁地铁一号线某站间线路为例，地铁列车参数如表1所示，线路参数如表2所示。列车站间运行距离为1 567 m，运行时间为93.65 s，线路中包括了直道、弯道、坡道等复杂路况，列车限速为80 km/h。首先采用线路纵断面化简原理，将实际线路化简为6段(1、14号区段分别为出站段和进站段，不予简化)，1号区段为等效路段a；2，3，4号区段为等效路段b；5，6，7，8号区段为等效路段c；9，10，11号区段为等效路段d；12，13号区段为等效路段e；14号区段为等效路段f，化简后的线路参数如表3所示。

表1 列车性能参数

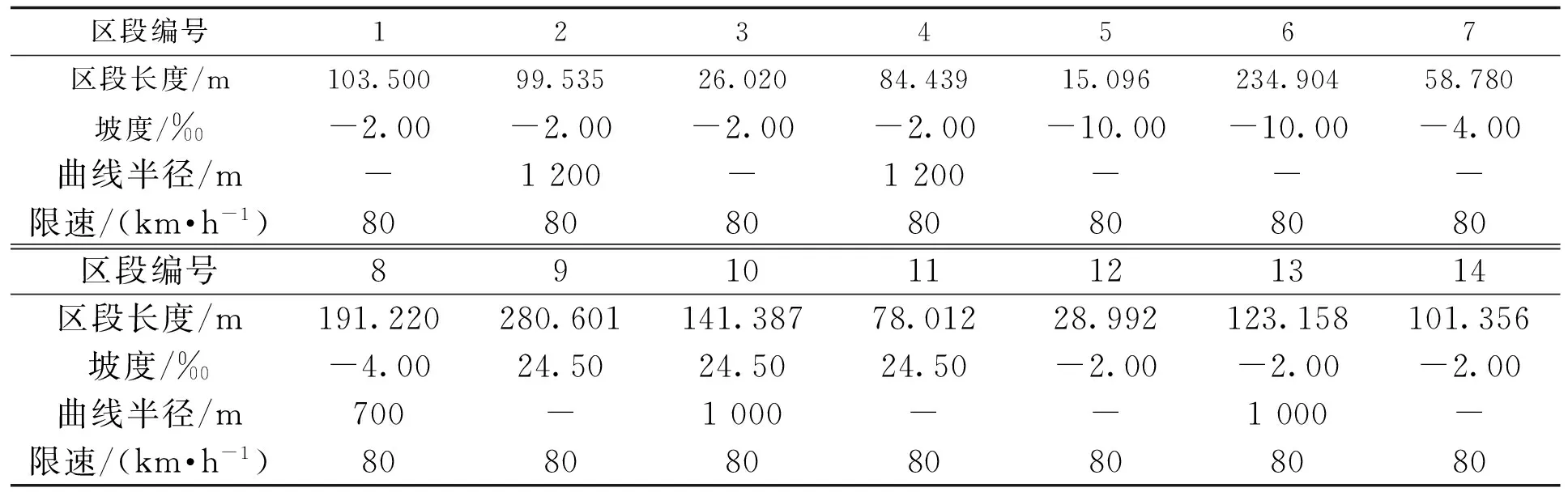
表2 某站间线路参数

表3 纵断面化简后的线路参数

根据列车不同运行工况与路况构建列车能耗函数，并满足列车站间运行距离与准点时间等约束，通过MATLAB平台仿真改进量子粒子群算法，求解能耗函数，得到列车最优匀速速度及各工况转换点的位置坐标与时间点，最终获取列车站间运行的最低能耗。工况转换点如表4所示，列车优化前后的运行数据如表5所示，列车运行的速度—距离(v-s)曲线与速度—时间(v-t)曲线，如图4所示。图4中,vm为列车最优匀速速度，且vm=75.52 km/h。

由表5中数据可得，经QPSO算法优化后的列车站间运行能耗在以50%再生能量回收的情况下，降低了9.21%，且符合准点停靠要求。该算法计算精度高，收敛速度快，并可以根据不同的站间线路与运行时刻表，实时获取不同的节能优化策略。同时解决了标准粒子群算法中粒子更新的盲目性，以及难以覆盖整个可行空间等问题；弥补了遗传算法编码过程复杂、运算量大，模拟退火算法收敛速度慢、参数选取缺乏理论依据等不足。

表4 列车最优运行策略

表5 列车运行数据

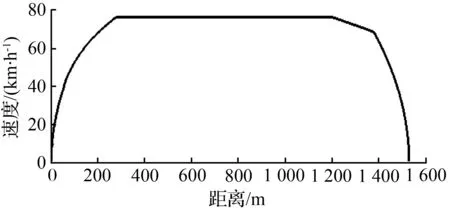
(a) 速度—距离曲线

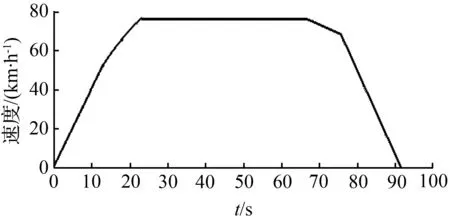
(b) 速度—时间曲线

图4 列车运行曲线图

Fig.4 Operating curve of train

4 结 论

①本文通过对地铁列车进行动力学分析，并根据列车节能优化原则建立多目标多约束的能耗模型。采用改进的量子粒子群优化算法求解既定时刻表下的定时节能模型，解决了已有研究成果中节约能耗和准点运行难以平衡的问题。该算法运算速度快，精度高，并且可以嵌入列车自动驾驶系统(ATO)中，具有良好的兼容性和稳定性。

②通过调整列车站间运行状态，充分利用再生制动能量，对传统列车节能优化中单纯采用“增加惰行—减少牵引”模式而忽略再生制动能量利用的方法，进行了有效改进。

③应用南宁地铁一号线某站间运行数据及线路参数进行实例仿真，降低列车能耗达9.21%。且该方法可以根据列车运行时刻表实时更新节能驾驶策略，实现了列车的在线节能优化，并适用于不同的运行线路。

[1] 唐海川, 王青元, 冯晓云.地铁列车追踪运行的节能控制与分析[J]. 铁道学报, 2015(1): 37-43.

[2] 李波, 王自力, 吴娜.基于遗传算法的列车优化操纵曲线研究[J]. 系统仿真技术, 2007(4): 192-196.

[3] BOCHARNIKOV Y V, TOBIAS A M, ROBERTS C. Reduction of train and net energy consumption using genetic algorithms for trajectory optimization[C]// DICKON R. IET Conference on Railway Traction Systems (RTS 2010). Birmingham, England: IET Digital Library, 2010:1-5.

[4] 余进,何正友,钱清泉.基于微粒群算法的多目标列车运行过程优化[J]. 西南交通大学学报, 2010, 45(1): 70-75.

[5] 熊超彬.基于GSO算法的列车运行节能操纵优化研究[D]. 成都：西南交通大学, 2014.

[6] HAI N T. Evaluation of effect Pontryagin’s maximum principle for optimal control train by criteria of energy save[C]// LIN N. 2010 International Symposium on Computer, Communication, Control and Automation (3CA). Tainan, China: IEEE, 2010: 363-366.

[7] HWANG H S.Control strategy for optimal compromise between trip time and energy consumption in a high-speed railway[J]. Systems Man & Cybernetics Part A Systems & Humans IEEE Transactions on, 1998, 28(6):791-802.

[8] WU Y.Energy-saving optimization of train on urban rail transit network[J]. Journal of Information & Computational Science, 2015, 12(9):3445-3453.

[9] 崔世文, 冯晓云.列车优化操纵与自动驾驶模式的研究与仿真[J]. 铁道机车车辆, 2005, 25(5):9-12.

[10]韩龙涛.地铁列车牵引计算与仿真[D]. 北京：北京化工大学, 2014.

[11]安志强.ATO目标速度曲线优化及跟随控制研究[D]. 成都：西南交通大学, 2011.

[12]黄舰,曲健伟.地铁列车基于惰行控制的节能优化运行研究[J]. 机车电传动, 2015(3):69-73.

[13]曹岩,孟学雷.基于改进差分算法的高速列车运行调整研究[J]. 铁道科学与工程学报, 2014,11(6): 102-108.

[14]张文丽,李群湛,刘炜,等.地铁列车再生制动节能仿真研究[J]. 变流技术与电力牵引, 2008(3): 41-44.

[15]李盼池,王海英,宋考平,等.量子势阱粒子群优化算法的改进研究[J]. 物理学报, 2012, 61(6): 1-10.

[16]乐美龙,黄薇.基于粒子群算法的泊位分配集成优化研究[J]. 广西大学学报(自然科学版), 2013, 38(1):119-124.

(责任编辑 梁 健)

Research on energy saving optimization operation of metro train based on improved QPSO algorithm

WANG He-liang1, HE De-qiang1, MO Zhi-gang2, MIAO Jian1

(1.College of Mechanical Engineering, Guangxi University, Nanning 530004, China; 2.Nanning Rail Transit Group Co.Ltd,Nanning 530021, China)

The operation optimization of metro train is an important way to save energy. According to the operation characteristics of metro train in different operation and line conditions, dynamic analysis is carried out on it. The lines are simplified based on the simplification principle of the line longitudinal profile. And the energy consumption model of actual conditions is built by combining the principle of energy-saving operation of the train with the constraint conditions between stations. Through applying the improved quantum particle swarm optimization (QPSO) algorithm, the speed and acceleration are coded in real number, the lowest energy consumption of train is acquired by iterative refinement and mutation. The characteristic parameters of the train are obtained, such as optimum constant speed and coasting point. The simulation examples of a line of Nanning metro line 1 proves that the method can effectively reduce the energy consumption of train up to 9.21% while ensuring the comfort, safety and punctuality.

optimization operation; energy-consuming model; quantum particle swarm optimization (QPSO); iterative refinement

2016-04-15；

2016-05-13

国家自然科学基金资助项目(51165001);广西科技攻关项目(桂科攻1598009-6);南宁市科技攻关项目(20151018)

贺德强(1973—)，男，湖南桃江人，广西大学教授，博士生导师；E-mail:hdqianglqy@126.com。

王合良，贺德强，莫志刚，等.基于改进QPSO算法的地铁列车节能优化操纵研究[J].广西大学学报(自然科学版)，2016，41(5)：1394-1401.

10.13624/j.cnki.issn.1001-7445.2016.1394

TP391.9；U260

A

1001-7445(2016)05-1394-08