具有时变时延网络控制系统的H∞控制器设计

宋 娟,蒋全胜

(1.苏州科技大学数理学院， 江苏苏州215009; 2.苏州科技大学机械工程学院， 江苏苏州215009)



具有时变时延网络控制系统的H∞控制器设计

宋 娟1,蒋全胜2

(1.苏州科技大学数理学院， 江苏苏州215009; 2.苏州科技大学机械工程学院， 江苏苏州215009)

在考虑含有外界噪声输入的情况下,研究了一类具有时滞网络控制系统的H∞控制问题。在网络环境中,将含时变时延的网络控制系统建模成一类受时变参数影响的闭环离散时间系统，基于Lyapunov理论和线形矩阵不等式(LMI)方法, 提出了此类系统H∞控制器的设计方法。该H∞控制器能有效地提高网络控制系统的鲁棒性,并保证系统渐进稳定。通过仿真方法证明了该方法的有效性。

网络控制系统;时延;H∞控制;Lyapunov原理;LMI

网络控制系统(networked control system,NCS)是指由实时网络为形成闭环反馈的控制系统。由于其结构简单、灵活, 网络控制系统在信息科学、生命科学及军事、航空航天等诸多领域得以广泛应用。然而, 网络控制系统中不可避免地存在网络诱导时延、数据包丢失、时绪错乱等不确定因素[1-3], 这不但给系统性能带来消极影响,甚至可能导致系统失去稳定。近年来,带时延的网络控制系统控制问题已成为控制领域的一个热点[4-17]。

针对一类具有随机时延的NCS, 文献[4]提出了基于队列预报的延时补偿方法,即通过采用在控制器和执行器节点端各自设立缓冲区的方法,将时变延时转化为固定延时。文献[5]使用一类带有多重连续时延成分的时延模型,在网络环境中提出了一种新的时延系统论方法。文献[6]采用了一类新的网络预报控制策略,提出了含任意时延的网络化系统的稳定性判据。文献[7]针对随机延时,提出了延时估计和在线获得延时数据的两种方法。先利用Z变换处理延时,由等价关系产生残差;再通过参数设计解耦干扰向量,从而对网络化控制系统的故障进行了有效判断。文献[8]将同时考虑网络时延和通信受限,将线性NCS等价地建模为一类线性时变系统,研究了其控制器和通信策略的设计问题。文献[9]建立了广义的被控对象的离散模型,结合Lyapunov 理论及线性矩阵不等式方法推导了闭环系统渐近稳定的充分条件。文献[12]研究了具有Markov 跳变参数的闭环供应链(closed-loop supply chain, CLSC)的切换网络控制系统建模以及具有抑制牛鞭效应的H∞控制问题。文献[14]将网络控制系统的未知短时延处理成范数有界不确定性, 结合Markov 丢包影响，将网络控制系统建模为不确定Markov 跳变系统, 设计了模态依赖的鲁棒故障检测滤波器。同时考虑时延和丢包问题，文献[15]针对一类离散时间网络化控制系统模型设计了具有时滞补偿的输出反馈控制器。文献[18]和文献[19]在考虑信道噪声干扰的情况下,研究了一类连续时间网络化控制系统的H∞控制问题。文献[18]将网络时延描述成Markov链形式,利用随机理论证明了连续时间NCS的H∞控制器的存在问题。文献[19]将具有时变采样和时延的NCS建模成一类离散动态区间系统, 并在此基础上设计了H∞控制器。但是文献[18]和文献[19]中建立的网络化控制系统模型均未涉及到不确定参数问题。

本文针对一类具有外界噪声输入的时延网络控制系统,研究了其控制问题。首先，将具有时变时延的网络控制系统建模为一类带不确定参数的闭环离散时间系统模型。 接着，结合Lyapunov理论和线性矩阵不等式方法，基于时滞依赖法提出了控制器设计方法。最后,通过仿真算例阐明了本文方法的有效性。

1 具有时变时延的NCS建模

NCS基本结构如图1所示。

图1 网络控制系统的基本结构

在图1中,τsc代表传感器—控制器端时延,τca表示控制器—执行器端时延。总的诱导时延为τ=τsc+τca。考虑如下所示的线性被控对象:

(1)

其中x∈Rn,u∈Rm,y∈Rr和ω(t)∈L2[0,∞)∈Rp分别表示状态，控制输入，输出向量及外界噪声输入,Ao,Bo,C和Ho为适当维数的矩阵。为了便于进一步讨论，现作如下假设：

假设1 在数据传输过程中采用单包传输。且不考虑数据包丢失和时序错乱问题。

假设2 在传输过程中存在时变时延，时延有界且不超过采样周期, 即τ(t)∈[0,T], 其中T为采样周期。

假设3 传感器使用时间驱动, 控制器、执行器均由事件驱动。

网络控制系统中信号传输时序如图2所示。基于NCS的结构和如上假设, 在一个采样周期内, 系统的输入不是一个单一的常数,而是一个分段的常数。

图2 NCS中的信号传输时序

在一个周期内, 控制输入可以表示为：

(2)

其中tk是第k个采样时刻,τk是对应的时延。根据以上所述,系统(1)可以等价于如下离散模型:

(3)

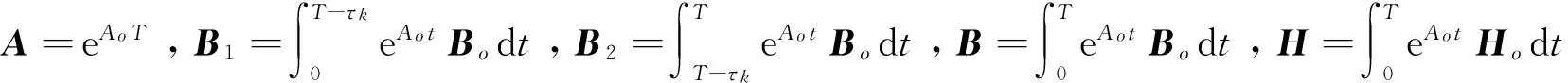
(4)

假设系统状态完全可测,采用如下状态反馈：

u(k)=Kx(k),

(5)

将式(5)带入式(4)便可得闭环系统模型：

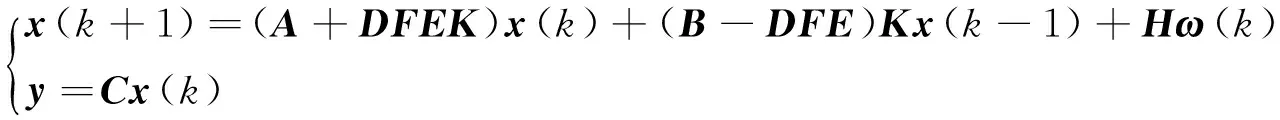
(6)

本文将讨论受外界噪声输入影响的NCS的H∞稳定性。

2 H∞控制器设计

定义1 对于系统 (6),若存在K使得：①当ω(k)=0时,闭环系统(10)渐近稳定;②在任意0初始条件下, 给定γ>0, 对于任意非0向量ω(k)∈L2[0,∞),输出y(k)满足‖y(k)‖2≤γ‖ω(k)‖2。则称K为NCS(6)的H∞控制增益,且γ是H∞范数[16]。

引理1 对于任意矩阵W,M,N,F(t)，满足FTF≤I[17]，给定常数ε>0, 则如下不等式成立:

W+MF(t)N+NTFT(t)MT≤W+εMMT+ε-1NTN。

(7)

定理1 对于系统(6), 若存在正定对称矩阵X和S, 以及常数ε>0和μ>0, 满足如下线性矩阵不等式：

(8)

证明 首先选取Lyapunov函数如下：

v(k)=xT(k)Px(k)+xT(k-1)Qx(k-1),

(9)

其中P,Q均为正定对称矩阵。

沿系统(5)的任意轨线向前作差分必有:

Δv(k)=v(k+1)-v(k)=xT(k+1)Px(k+1)-

xT(k)(P-Q)x(k)-xT(k-1)Qx(k-1)=

[(A+DFEK)x(k)+(B-DFE)Kx(k-1)+

Hω(k)]TP[(A+DFEK)x(k)+(B-DFE)Kx(k-1)+

Hω(k)]-xT(k)(P-Q)x(k)-xT(k-1)Qx(k-1)。

(10)

将式(10)改写成矩阵形式为：

(11)

其中：

Φ11=(A+DFEK)TP(A+DFEK)-P+Q+CTC;

Φ12=(A+DFEK)TP(B-DFE)K;

Φ13=(A+DFEK)TPH;

Φ22=[(B-DFE)K]TP(B-DFE)K-Q；

Φ23=[(B-DFE)K]TPH;

Φ33=HTPH-γ2I。

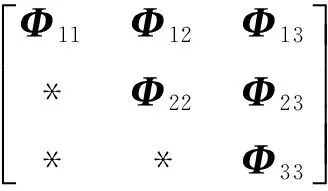
(12)

根据引理1可知,

(13)

现考虑:

(14)

结合式(13)和Schur补充原理可知,若式(14)成立,式(12)必成立。再由式(11)可知,必有Δv(k)+yT(k)y(k)-γ2ωT(k)ω(k)<0。当ω(k)≡0时,显然Δv(k)<0;再根据0初始条件可知,v(0)=0。 由于v(∞)≥0，故有:

(15)

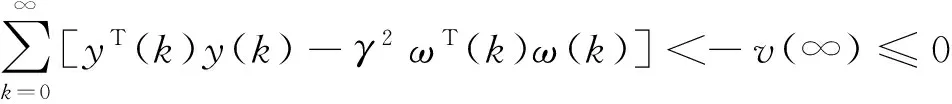
(16)

即‖y(k)‖2<γ‖ω(k)‖2。根据定义 1可知,NCS(6) 渐进稳定且具有H∞范数γ。将式(14)两边分别左乘、右乘diag(I,I,P-1,P-1,I),令X=P-1,W=KP-1=KX,S=P-1QP-1,γ2=μ, 并使用Schur补充原理便可得不等式(8)。因此，定理得证。

3 仿真算例

考虑如下倒立摆模型：

选取采样周期T=0.1s。选择参数α1=1.631,α2=-1.682,α3=-2.135,α4=1.688。按文献[10]的计算方式可得:

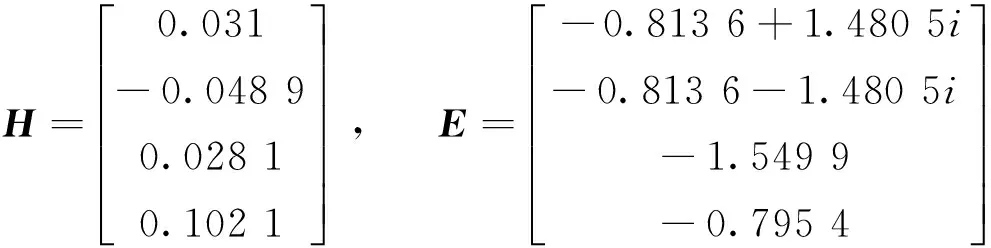
进一步地，使用文献[16]中所提出的方法,可得控制增益K=[2.075 8 -0.536 4 0.289 6 -3.617 8],在同一系统初始条件下,可得系统状态响应如图5所示,由图5可知,在该控制策略下系统所有状态均是发散的。通过对比，进一步阐明了该H∞性能控制方法的有效性和可行性。

图3 NCS中的时变时延

Fig.3 Time-varying delay in NCS

图4 NCS的状态响应

Fig.4 State response of NCS

4 结 语

本文基于网络传输环境将网络控制系统建模为闭环的离散系统,并将时变诱导时延建模为一类时变参数。结合Lyapunov稳定性理论和矩阵不等式原理,在考虑外界噪声输入的影响下,提出了此类系统的H∞控制器的设计方法。根据仿真算例可知,该控制方法对外界噪声有良好的抑制作用,从而验证了此方法的有效性。

[1] LUAN X, SHI P, LIU F.Stabilization of networked control systems with random delays[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9):4323-4330.

[2] MA C, SHI P, ZHAO X, et al.Consensus of Euler-Lagrange systems networked by sampled-data information with probabilistic time delays[J]. IEEE transactions on cybernetics, 2015, 45(6): 1126-1133.

[3] WANG Z, YANG F, HO D W C, et al.Robust H∞control for networked systems with random packet losses[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 2007, 37(4): 916-924.

[4] LUCK R, RAY A.An observer-based compensator for distributed delays[J]. Automatica, 1990, 26 (5): 903-908.

[5] GAO H, CHEN T, LAM J.A new delay system approach to network2based control[J]. Automatica, 2008, 44 (1):39-52.

[6] LIU G P, REES D.Stability criteria of networked predictive control systems with random network delay[C]//Proceedings of the 44th IEEE Conference on Decision and Control. Seville, Spain: IEEE, 2005: 203-208.

[7] 郑英,方华京,谢林柏,等.具有随机时延的网络化控制系统基于等价空间的故障诊断[J]. 信息与控制, 2003, 32(2): 155-159.

[8] ZHANG L, HRISTU-VARSAKELIS D.Communication and cont rol co-design for networked control systems[J]. Automatica, 2006, 42 (6): 953-958.

[9] 樊卫华,蔡骅,陈庆伟,等.时延网络控制系统的稳定性[J]. 控制理论与应用, 2004, 21 (6): 33-37.

[10]谢成祥,樊卫华,胡维礼.一类短时延网络控制系统的建模和控制方法[J]. 南京理工大学学报(自然科学版), 2009, 33(2)：156-160.

[11]薛东国,陈博,张文安,等.通信受限下网络化多传感器系统的Kalman融合估计[J]. 自动化学报, 2015, 41(1): 203-208.

[12]李庆奎,李梅,贾新春.具有 Markov 跳变参数的闭环供应链系统切换控制[J]. 自动化学报, 2015, 41(12): 2081-2091.

[13]詹习生,吴杰,关治洪,等.基于丢包和带宽限制网络化系统稳定性分析[J]. 控制理论与应用, 2014,31(8):1111-1115.

[14]王昭磊,王青,董朝阳,等.存在未知时延和Markov丢包的网络控制系统故障检测与优化[J]. 控制与决策, 2014, 29(9): 1537-1544.

[15]ZHU Q, LU K, ZHU Y.Observer-based feedback control of networked control systems with delays and packet dropouts[J]. Journal of Dynamic Systems, Measurement, and Control, 2016, 138(2): 2-11.

[16]KARIMI H R, GAO H.New delay-dependent exponential H∞synchronization for uncertain neural networks with mixed time delays[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2010, 40(1): 173-185.

[17]ZHU Q, LU K, ZHU Y.H∞guaranteed cost control for networked control systems under scheduling policy based on predicted error[J]. Mathematical Problems in Engineering, 2014,23:1-14.

[18]韦庆阳,樊春霞,顾瑜.带有通信噪声的随机时延复杂动态网络的H∞控制[J]. 应用科学学报, 2014, 32(6): 639-644.

[19]陈惠英,李祖欣,王培良.具有时变采样周期和时延的NCS的H∞控制[J]. 中国自动化学会控制理论专业委员会(B卷), 2011:1-5.

(责任编辑 梁碧芬)

H∞controller design of networked control systems with time variant delay

SONG Juan1, JIANG Quan-sheng2

(1. School of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou 215009, China; 2. School of Mechanical Engineering, Sozhou University of Science and Technology, Suzhou 215009, China)

The problem of H∞control of delayed networked control systems with outside disturbance is discussed. Based on the network transmission environment, the networked control system with time variant delay is firstly modeled as a closed loop discrete-time system with time variant parameters. Then, based on Lyapunov stability theory and linear matrix inequality (LMI) approach, the design of H∞controller is proposed, which helps to enhance the robustness of NCS and renders it be asymptotically stable. Finally, the validity of the method is proved by simulation.

networked control system; delay;H∞control; Lyapunov theory; LMI

2016-05-27；

2016-07-01

国家自然科学基金资助项目(51375323);苏州市科技计划资助项目(SYN201509)

蒋全胜(1978—)，男,湖北洪湖人，苏州科技大学副教授，博士;E-mail:qschiang@163.com。

宋 娟,蒋全胜.具有时变时延网络控制系统的H∞控制器设计[J].广西大学学报(自然科学版)，2016，41(5)：1493-1499.

10.13624/j.cnki.issn.1001-7445.2016.1493

TP273

A

1001-7445(2016)05-1493-07