基于转矩角正切值的车用异步电机转子时间常数辨识

倪荣来，李军伟，高 松

(山东理工大学交通与车辆工程学院， 山东淄博255049)



基于转矩角正切值的车用异步电机转子时间常数辨识

倪荣来，李军伟，高 松

(山东理工大学交通与车辆工程学院， 山东淄博255049)

针对异步电机转子时间常数随温度和磁场饱和而变化，从而破坏定子电流励磁分量和转矩分量解耦条件，影响按转子磁链定向间接矢量控制系统动、静态性能的问题，提出了一种通过对比给定转矩角正切值与反馈转矩角正切值，并利用PI控制器来实时辨识异步电机转子时间常数的方法。对转矩角正切值与转子时间常数之间的关系进行了理论分析，推导了异步电机反馈的转矩角正切值计算公式，建立了MATLAB/Simulink环境下异步电机矢量控制系统的数学模型及基于转矩角正切值的转子时间常数辨识模型，并进行了仿真验证。仿真结果表明，这种基于计算转矩角正切值的异步电机转子时间常数辨识方法能够准确辨识出电机的实际转子时间常数，验证了该方法的正确性和可行性。

电动汽车；异步电机；矢量控制；转子时间常数辨识；仿真

由于高可靠性和低成本的特性，异步电机已成为电动汽车应用最广泛的驱动电机之一[1]。异步电机是一个强耦合、多变量、高阶非线性的系统[2-5]。间接磁链定向矢量控制将定子电流转化为同步旋转坐标系上的两个直流分量，实现了电机转矩和磁链的解耦控制，使异步电机具有了同直流电机相当的动、静态性能，这使其在高性能驱动系统中的应用日益广泛。矢量控制的精确控制依赖于准确的电机参数[6-7]。在电动汽车行驶过程中，驱动电机参数的变化将会引起不准确的磁链定向，进而影响矢量控制的性能。在异步电机的各项参数中，对磁链定向影响最大的是转子时间常数[8-9]。因此，在线辨识出准确的转子时间常数是保证矢量控制性能充分发挥的关键。

自按转子磁链定向矢量控制问世以来，为了获得矢量控制最佳的调速性能，国内外很多学者对转子时间常数在线辨识进行了研究。目前转子时间常数在线辨识方法主要分为基于信号注入的频谱分析法、模型参考自适应辨识法[2,10-11]、基于观测器(扩展卡尔曼滤波器[12]，扩展龙贝格观测器[13])的辨识法。文献[14]结合电压和电流磁链模型，并利用小信号注入的转子时间常数辨识方法，克服了电机低速轻载时转子时间常数辨识不准确的问题，但没有考虑磁链开环控制时转子时间常数辨识的问题。文献[15]采用定子磁链模型辨识转子时间常数，优化了模型参考自适应辨识法，增强了电机的鲁棒性，但没有考虑转子电感变化对转子时间常数产生的变化。文献[16]分析了转子时间常数对异步电机转矩电流比的影响，为判断转子时间常数辨识的准确性提供了理论依据，但没有给出具体的辨识方法。

转子电阻在电机运行过程中会随温度的变化而变化，同时也受磁链饱和的影响。转子电感在电机轻载和重载时也会发生变化。转子电阻和电感的变化都会引起转子时间常数的变化，本研究基于文献[16]及模型参考自适应的思想，提出一种基于转矩角正切值计算的转子时间常数辨识新方法。该方法是通过对比转矩角正切值的参考值和估算值，利用PI调节来实时辨识转子时间常数，将转子电阻和电感变化引起的转子时间常数的变化进行了统一调节，具有较强的鲁棒性，为异步电机转子时间常数辨识提供了一种新方法。

1 间接磁链定向矢量控制

异步电机的非线性特性增加了对其控制的难度。坐标变换可以简化异步电机数学模型，以便分析和计算。实际应用中，将任意旋转坐标系(dq)与转子磁链矢量同步旋转，使d轴与转子磁链矢量重合，便得到了按转子磁链定向的同步坐标系。在按转子磁链定向同步旋转坐标系中，异步电机转矩可表示为：

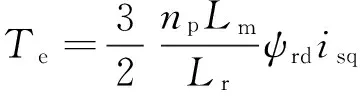
(1)

在稳态时，转子磁链的幅值为：

ψrd=Lmisd，

(2)

式中，np为电机极对数；Lr为转子电感；Lm为转子和定子间的互感；isd，isq分别为励磁电流和转矩电流；因此，磁链和转矩的解耦控制可以通过控制d轴电流(励磁电流)和q轴电流(转矩电流)来实现。给定的励磁电流与反馈的励磁电流通过PI调节产生励磁电压usd，给定的转矩电流(可通过速度控制器产生)与反馈的转矩电流通过PI调节产生转矩电压usq。将异步电机电流解耦为励磁电流和转矩电流所用的转子磁链定向角度为：

θe=∫ωedt，ωe=ωs+ωr，

(3)

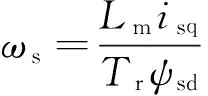
(4)

式中，ωe为同步旋转坐标系角速度(rad/s)；ωs为转差角频率(rad/s)；ωr为转子角速度(rad/s)；Tr为转子时间常数(s)，Tr=Lr/Rr，Rr为转子电阻(Ω)。

由以上分析可知，精准的间接磁链定向矢量控制依赖于精确的转子时间常数计算。对转子时间常数估算的偏差会导致转子磁链位置估算的偏差，从而造成励磁电流和转矩电流不能完全解耦，进而导致瞬态转矩性能的下降和错误的磁链幅值，致使电机损耗增加，电机的最大可用扭矩减少。因此，为保证励磁和转矩电流能够实时准确解耦，电机实时可以获得最佳的动态性能，对转子时间常数进行在线辨识是必不可少的[16]。

2 转矩角正切值

2.1 转矩角正切值参考值

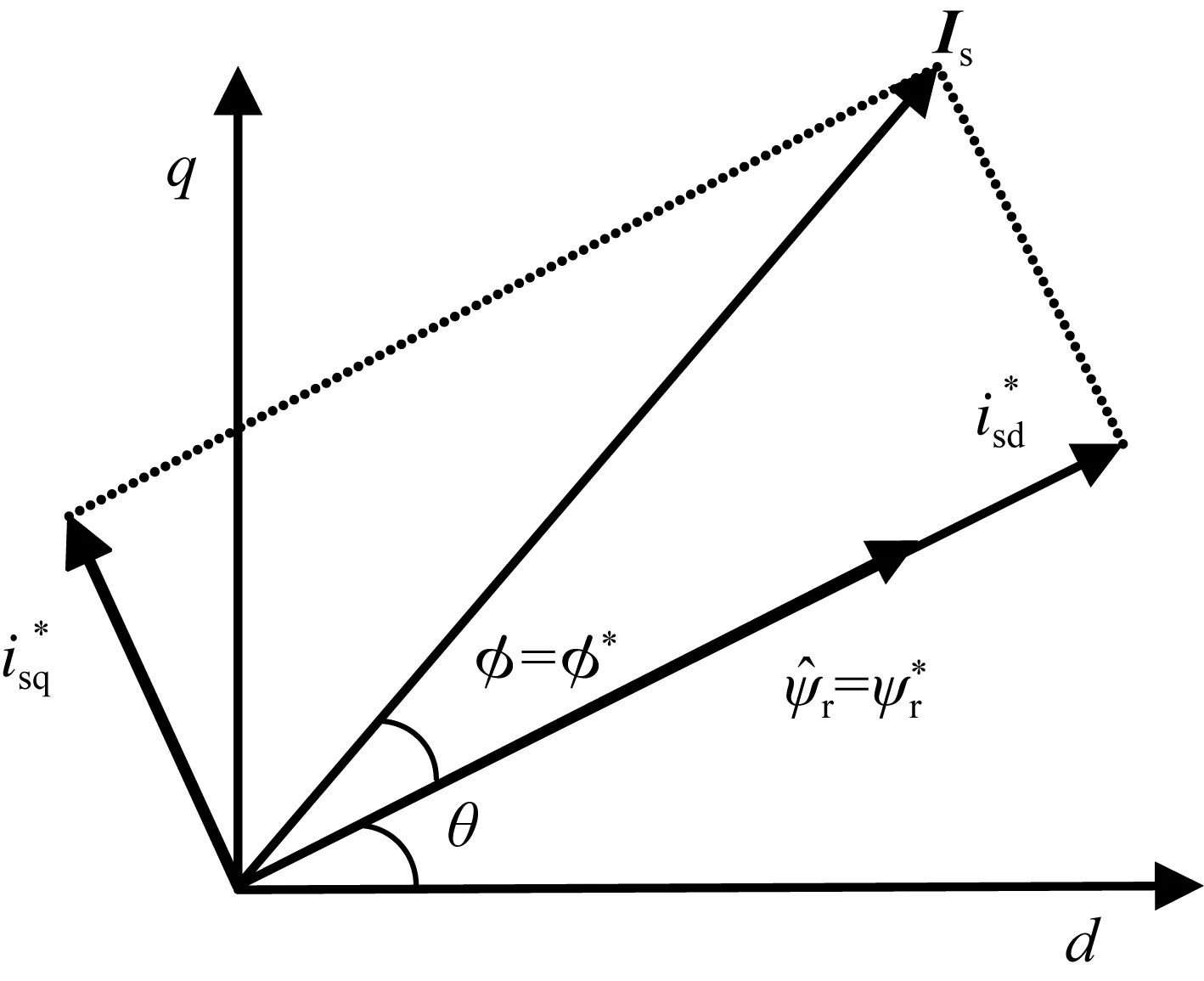
图1 定子电流矢量与转子磁链矢量的夹角Fig.1 The angle between the stator current vector and the rotor flux vector

2.2 实际转矩角正切值在线计算

用旋转的绕组代替原来静止的定子绕组，并使等效的转子绕组与等效的定子绕组相重合，且保持严格同步(等效后定、转子绕组间不存在相对运动)。变换后得到异步电机在任意旋转坐标系下的数学模型为：

电压方程：

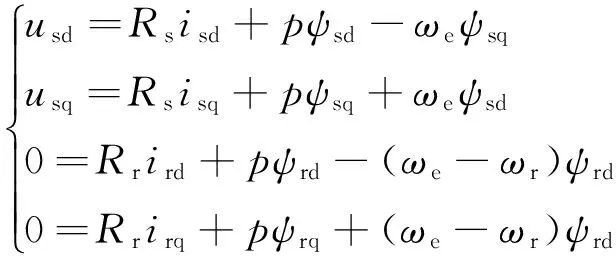
(5)

磁链方程：

(6)

转矩方程：

Te=npLm(isqird-isdirq)，

(7)

式中，Rs为定子电阻；Ls为定子电感；p为微分算子；ψsd和ψsq为定子磁链；ψrd和ψrq为转子磁链；isd和isq为定子电流；ird和irq为转子电流。

通过转子磁链方程重构定子磁链方程得：

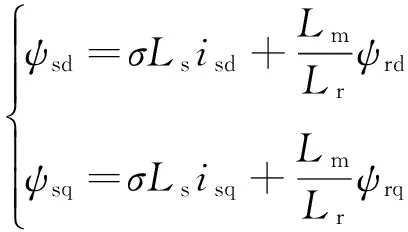
(8)

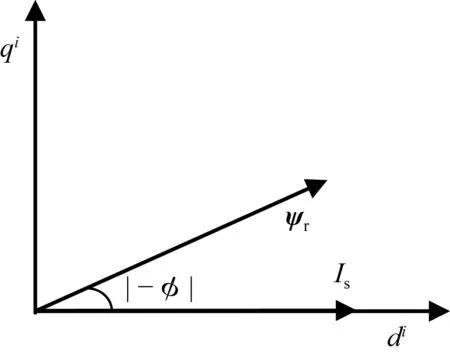
图2 定子电流坐标系Fig.2 Stator current coordinate

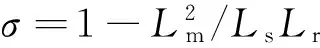
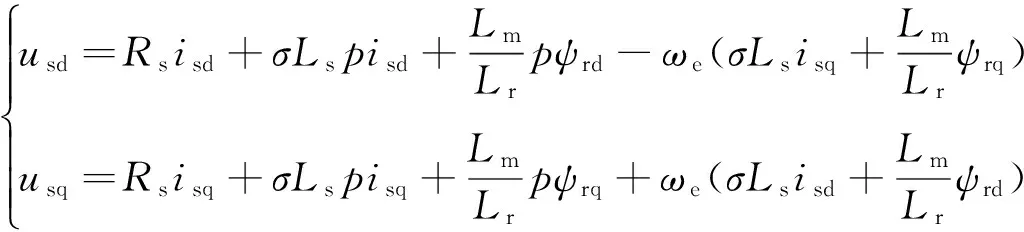
(9)

化简式(9)得：

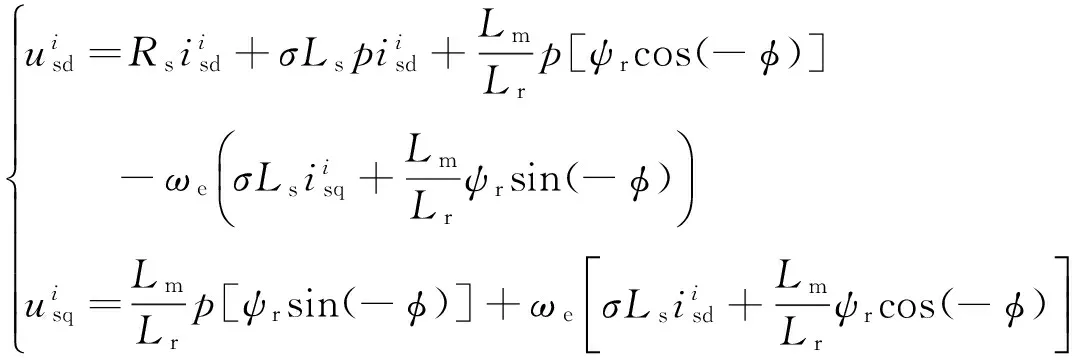
(10)

计算出上式中的微分项,得：

(11)

假设转子磁链恒定，重新计算上式,得：

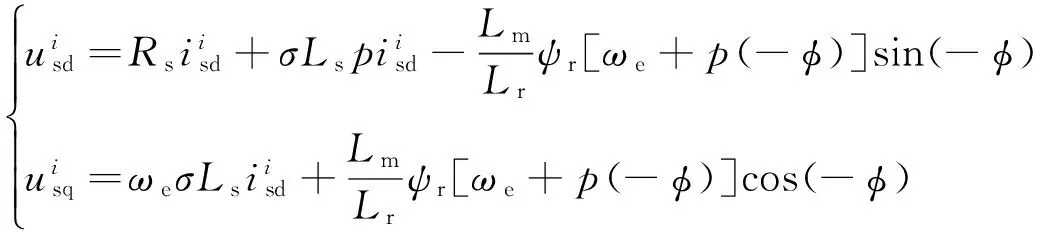
(12)

由式(12)可以计算出定子电流坐标系下转矩角的正切值为：

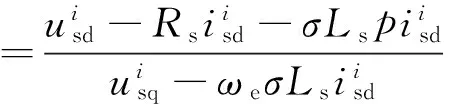
(13)

当转子磁链处于稳定状态时，该方程在整个电机工作范围内(包括弱磁区域)都可以准确计算出实时的转矩角正切值，为实时辨识转子时间常数提供依据。

定子电流矢量坐标系上的电压和电流可由两相静止坐标系上的电压和电流通过式(14)和式(15)计算得到，即：

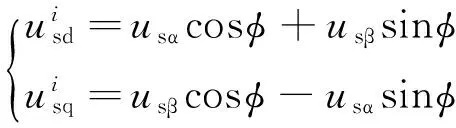
(14)

(15)

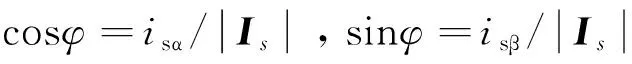
2.3 转子时间常数对转矩角正切值的影响

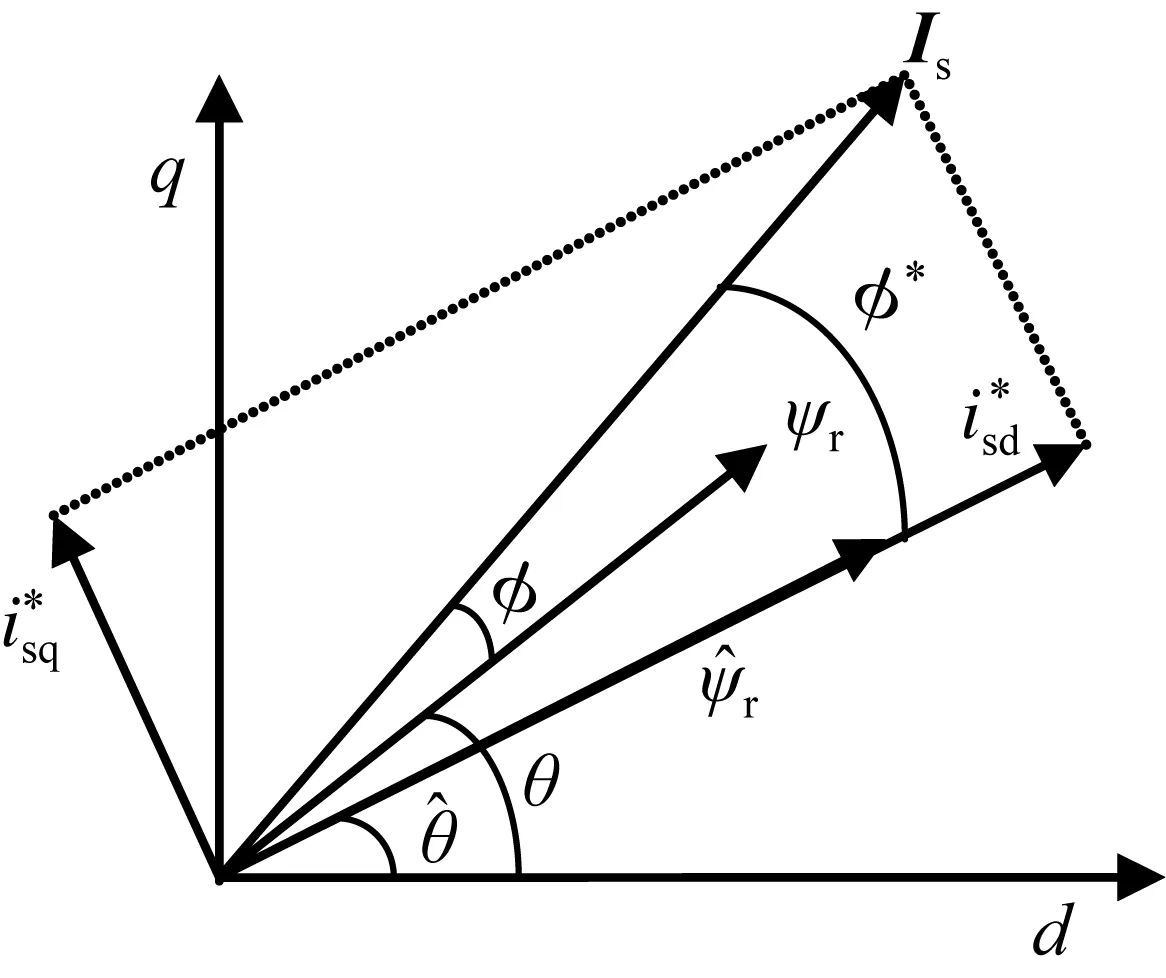
图3 估算的转矩角正切值小于给定值

Fig.3 The estimated torque angle tangent value is less than the given value

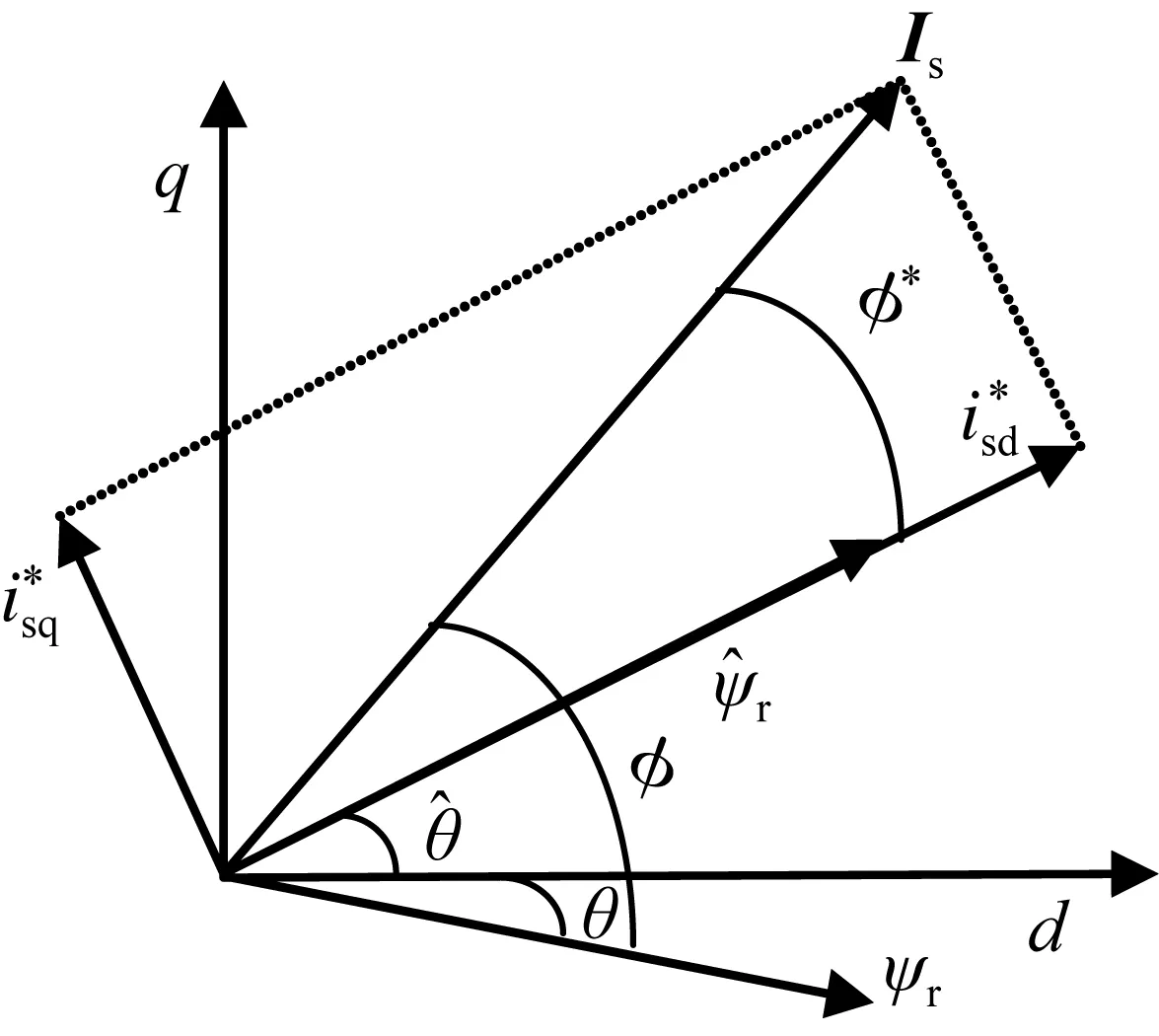
图4 估算的转矩角正切值大于给定值

Fig.4 The estimated torque angle tangent value is bigger than the given value

综上可知，通过对比估算的转矩角正切值和给定的转矩角的正切值可以判断转子时间常数的估算准确与否。进而，可以通过调整转子时间常数使得转矩角正切值的估算值和参考值相等。根据以上分析，可以建立带有转子时间常数辨识的按转子磁链定向矢量控制系统，整个控制系统框图如图5所示。

图5 基于转矩角正切值计算的转子时间常数辨识矢量控制系统框图

由式(13)可知，转矩角正切值的计算中含有电流微分项，且电机启动时电压和电流变化大。由于逆变器的作用，反馈的定子电流中含有高频变化成分，从而增强电流微分项的作用。微分项对电流测量中的高频干扰成分非常敏感，剧烈变化的电压和电流也会影响转子时间常数辨识效果，严重时会出现奇异问题。但考虑到电机参数因温度变化而变化的速度相对较慢，所以，转子时间常数辨识可以在速度稳定时进行或增加滤波器，这样能够有效过滤掉微分项产生的高频噪声，避免电机因转子时间常数的波动而产生转矩脉动以及系统震荡。

3 仿真验证

根据系统控制框图，利用MATLAB/Simulink搭建异步电机按转子磁链间接定向矢量控制系统模型和基于转矩角正切值计算的转子时间常数辨识模型。为了验证所提出的基于转矩角正切值的转子时间常数辨识方法的有效性，将在线辨识方法应用于异步电机间接磁链定向的矢量控制系统中进行仿真实验。

仿真所用的电机参数：转动惯量J=0.18 kg·m2，极对数np=2，定子电感Ls=0.071 H，转子电感Lr=0.071 H，定转子间的互感Lm=0.069 H，定子电阻Rs=0.435 Ω，转子电阻Rr=0.816 Ω。

为了验证基于转矩正切角计算的转子时间常数辨识法的快速性和准确性，设计两组转子时间常数跟踪实验。

①实验一：由Tr=Lr/Rr可知，可以通过改变转子电阻Rr的方法来改变转子时间常数Tr，以此来模拟电机运行过程中由于温度变化引起的转子时间常数的变化。

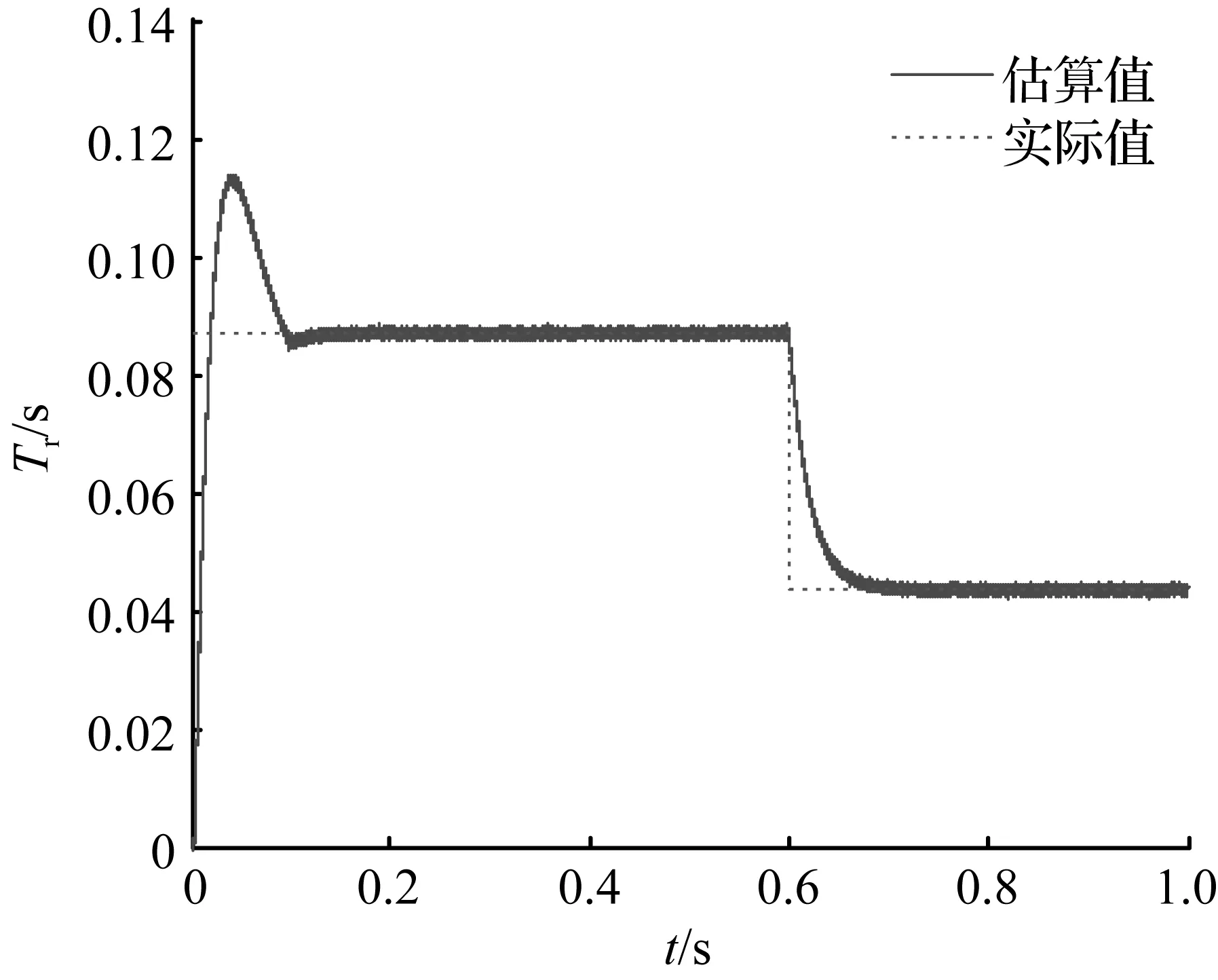
图6 转子时间常数辨识结果

Fig.6 Rotor time constant identification result

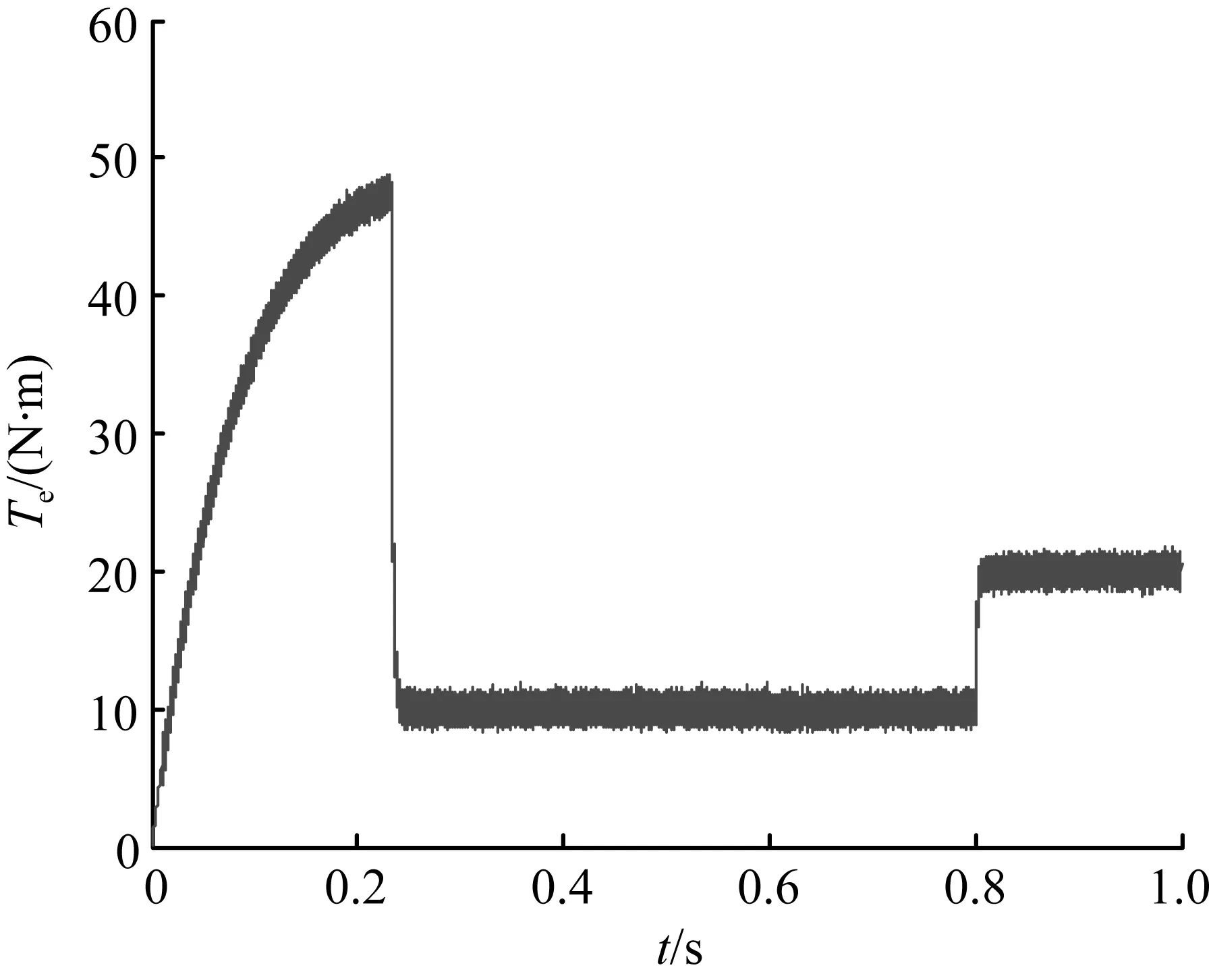
图7 异步电机转矩响应

Fig.7 Torque response of induction motor

在0～0.2 s中，电机处于启动加速阶段，电机的电压、电流和转矩变化的幅值较大，对电机冲击较大。由式(20)可知，此时计算出的转矩角正切值在电机启动阶段也会出现超调，致使PI控制器输出的转子时间常数出现超调。随着电机转速的增加，电压、电流和转矩的变化值趋于平稳，此时计算出的转矩正切角与给定值趋于相等，PI控制器输出的转子时间常数估算值很快达到实际值。在0.6 s时，转子时间常数以阶跃信号变化，转子时间常数辨识值能在0.15 s内达到实际值，并维持恒定，说明转子时间常数辨识方法优良的快速性、准确性。在0.8 s时，负载转矩突然增加，转子时间常数辨识值仍能较好地跟随实际值，表明这种辨识方法具有良好的稳定性。

②通过改变定子与转子间的互感Lm间接改变转子自感Lr，进而改变转子时间常数Tr来模拟电机运行过程中因温度升高而引起的转子自感的变化。并对文献[15]提出的基于定子磁链模型的转子时间常数辨识方法进行了对比验证。

在0.4 s之前，电机仿真工况与实验一相同。在0.4 s后，定子与转子间的互感Lm阶跃为初始值的25%，相应的转子时间常数阶跃约为初始值的1.25倍。本文所提出的辨识方法与基于定子磁链模型的辨识方法仿真结果如图8、图9所示。

由图8、图9可以看出，在0～0.2 s中，基于定子磁链模型的辨识方法比本文提出的辨识方法辨识的转子时间常数震荡时间长。在0.4 s时，电机互感发生阶跃变化，互感的阶跃变化不仅影响转子时间常数，还会引起磁链和转矩的波动，两种辨识方法辨识出的转子时间常数均出现了不同程度的震荡。与基于定子磁链模型辨识方法相比，本文的辨识方法无需经过磁链观测过程辨识转子时间常数，所以能在更短时间内以更小的超调量估算出转子时间常数实际值。

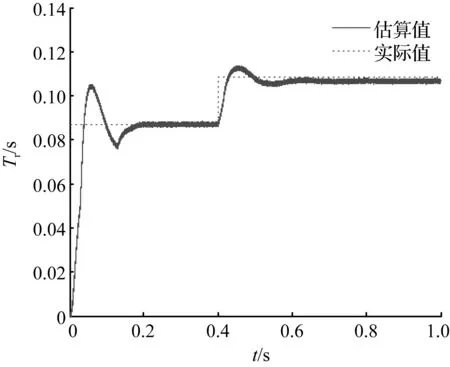
图8 基于定子磁链模型方法的辨识结果

Fig.8 Identification result of the method based on stator linkage model

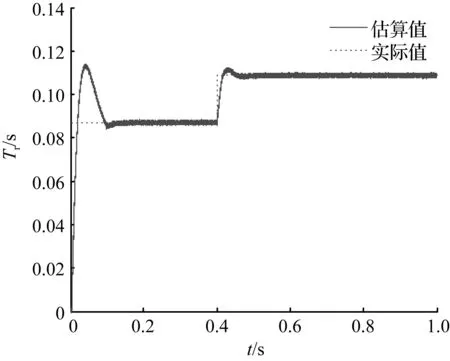
图9 本文所提方法的辨识结果

Fig.9 Identification result of the proposed method in the paper

4 结 语

本文提出一种基于转矩角正切值的电动汽车驱动用异步电机转子时间常数辨识方法，利用给定的转矩角正切值同反馈的转矩角正切值的差值，结合PI控制器辨识出实时的转子时间常数。将辨识出的转子时间常数应用到磁链开环转差型矢量控制系统中，能够更加准确地估算出实际转子磁链的位置，为定子电流的励磁分量和转矩分量充分解耦提供了条件，从而保证了矢量控制性能的充分发挥。仿真结果验证了这种方法能够在较短时间内辨识出电机的转子时间常数，并且辨识精度高，辨识速度快。

[1] 初敏, 高松, 杨坤,等.纯电动客车最佳制动能量回收控制策略研究[J]. 广西大学学报(自然科学版), 2015,40(2):357-366.

[2] 王高林, 杨荣峰, 张家皖,等.一种感应电机转子时间常数MRAS的在线辨识方法[J]. 电工技术学报, 2012,27(4):48-53.

[3] 崔霆锐, 张立伟.矢量控制异步电机参数敏感性仿真研究[J]. 计算机仿真, 2014, 31(7):187-192.

[4] 戴良伟.三相异步电机最优励磁电流矢量控制[D]. 杭州：浙江理工大学, 2013.

[5] 刁利军, 孙大南, 陈杰,等.间接矢量控制异步电动机参数敏感性分析[J]. 电工技术学报, 2010，25(6):18-23.

[6] PEREZ I, GOMEZ-GONZALEZ M, JURADO F.Estimation of induction motor parameters using shuffled frog-leaping algorithm[J]. Electrical Engineering, 2013, 95(95):267-275.

[7] 张杰, 柴建云, 孙旭东,等.基于参数在线校正的电动汽车异步电机间接矢量控制[J]. 电工技术学报, 2014, 29(7):90-96.

[8] ÇANAKOGLU A I, YETGIN A G, TEMURTAH, et al.Induction motor parameter estimation using metaheu-ristic methods[J]. Turkish Journal of Electrical Engineering & Computer Sciences, 2014, 22(5):1177-1192.

[9] TOLIYAT H, LEVI E, RAINA M.A review of RFO induction motor parameter estimation techniques[J]. IEEE Power Engineering Review, 2002, 18(7):52-52.

[10]任振华.基于模型参考自适应的异步电机转子电阻辨识[D]. 北京：北京交通大学, 2012.

[11]MAITI S, CHAKRABORTY C, HORI Y, et al.Model reference adaptive controller-Based rotor resistance and speed estimation techniques for vector controlled induction motor drive utilizing reactive power[J]. IEEE Transactions on Industrial Electronics, 2008, 55(2):594-601.

[12]RADHAKRISHNAN K, UNNIKRISHNAN A, BALAKRISHNAN K G.EM based extended kalman filter for estimation of rotor time-constant of induction motor[C]// IEEE International Symposium on Industrial Electronics. Montreal, Canada: IEEE, 2006:2434-2438.

[13]余夫良, 邓志奇, 陈阳生.一种感应电机参数自适应转子磁链观测器的设计[J]. 机电工程, 2011, 28(7):876-880.

[14]WANG K, CHEN B, SHEN G, et al.Online updating of rotor time constant based on combined voltage and current mode flux observer for speed-sensorless ac drives[J]. IEEE Transactions on Industrial Electronics, 2014, 61(9):4583-4593.

[15]刘和平,汤梦阳,刘庆,等.基于定子磁链模型的异步电机转子时间常数辨识[J]. 电机与控制学报, 2014,18(1):56-61.

[16]燕俊峰,王晓琳,廖启新.转子时间常数对异步电机转矩电流比的影响分析[J]. 电气传动, 2014,44(12):12-16.

[17]WANG K, CHIASSON J, BODSON M, et al.An online rotor time constant estimator for induction machine[J]. Control Systems Technology IEEE Transactions on, 2005, 15(2):339-348.

(责任编辑 裴润梅)

Rotor time constant identification of asynchronous motor for vehicle based on torque angle tangent value

NI Rong-lai, LI Jun-wei, GAO Song

(School of Traffic and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China)

In view of the problem that rotor time constant of asynchronous motor vary with temperature and magnetic field saturation so that broking the decoupling condition of excitation component and torque component of stator current and affecting dynamic and static performance in indirect rotor flux orientation vector control system, a new method of time constant identification based on comparing the tangent value of reference torque angle and the tangent value of feedback torque angle then by utilizing PI controller to identify the rotor time constant real-time is proposed. The relationship between the tangent torque and rotor time constant is analyzed while the calculation formula of feedback torque angle tangent is deduced. Then a mathematical model of the vector control system of asynchronous motor and the model of the rotor time constant identification are established and simulated in MATLAB/Simulink environment. The simulation result shows that the rotor time constant identification method based on calculating the tangent value of torque angle can accurately identify the rotor time constant of the motor in pretty short time and verify the correctness and feasibility of the method.

electric vehicle; asynchronous motor; vector control; rotor time constant; simulation

2016-04-12；

2016-05-15

山东省自然科学基金资助项目(ZR2015EM054)；山东省重点研发计划项目(2015GGX105009)

李军伟(1964—)，男，河南平顶山人，山东理工大学教授，博士；E-mail:ljwhitt@163.com。

倪荣来，李军伟，高松.基于转矩角正切值的车用异步电机转子时间常数辨识[J].广西大学学报(自然科学版)，2016，41(5)：1477-1484.

10.13624/j.cnki.issn.1001-7445.2016.1477

TM343

A

1001-7445(2016)05-1477-08