随机环境下连续泊位和岸桥集成分配问题研究

郝杨杨，刘天赐，黄有方

(上海海事大学物流研究中心， 上海201306)



随机环境下连续泊位和岸桥集成分配问题研究

郝杨杨，刘天赐，黄有方

(上海海事大学物流研究中心， 上海201306)

泊位和岸桥是集装箱港口非常最要的资源，对随机环境下连续泊位和岸桥进行合理的分派与调度可以有效地提高作业效率。考虑连续泊位上船舶离港延时惩罚、偏好泊位的影响，以最小化船舶总在港时间为目标，建立连续泊位和岸桥的集成分配模型。采用VC++开发仿真程序，以邻域搜索的重调度算法对模型进行求解。考虑船舶抵港时间和装卸时间具有一定的随机性，在最优解的基础上进行随机波动分析。实验结果显示，当抵港时间发生波动时，船舶靠泊计划的最大偏差值为2.7 h；而当装卸时间发生波动时，船舶靠泊计划的最大偏差值为42.9 h。实验表明，由装卸时间波动导致的船舶总在港时间偏差远大于由抵港时间波动导致的偏差，从而为船舶抵港与装卸不确定环境下的船舶靠泊计划制定提供理论依据。

随机环境；泊位—岸桥；连续泊位；偏好泊位；邻域搜索

0 引 言

泊位和岸桥是集装箱港口非常最要的资源，合理的分派与调度可以有效提高作业效率。实际作业中出于岸桥数量和岸桥成本限制，港口需要在最大限度的岸桥数量和有限泊位岸线下，进行集成资源优化配置来提高运行效率[1-2]。

在泊位和岸桥的集成分配问题中，目标函数通常是船舶总在港时间最小、总成本最小或是总等待时间最小。如Imai等[3-4]考虑到船舶服务的优先级，建立了以船舶最小化在港时间为目标的优化模型，提出通过遗传算法求解泊位分配问题。Frank Meisel等[5]采用岸桥的装卸效率代表船舶的处理时间，研究了泊位和岸桥的联合分配问题。梁承姬等[6]将船舶处理时间用岸桥装卸的速度来表示，研究了泊位和岸桥整合分配问题。乐美龙等[7]研究了基于泊位偏好与服务优先级的泊位和岸桥分配问题。将离散泊位连续化可以最大限度的提高泊位利用率，Kim等[8]构建MIP模型研究连续泊位分配问题，并用模拟退火算法和LINDO进行求解。韩晓龙等[9]建立了泊位分配的混合整数规划模型以及桥吊调度的混合整数规划模型，讨论了连续泊位和岸桥的协同分配问题。

以上是针对确定性的泊位分配问题进行的研究，但船舶的到港时间、装卸时间、装卸工作量等都具有不确定性，但如频繁地修正靠泊计划则会降低码头的作业效率、增加码头的经营成本。关于随机性的研究，Moorthy等[10]基于序列对编码的方法，使用项目评审技术的理论对连续岸线下的随机泊位分配问题进行了求解。曾庆成等[11]采用干扰管理的方法，考虑码头作业成本、船舶等待成本与计划偏离度三个方面的系统扰动，构建了泊位分配与装卸桥调度的干扰管理模型。蒋大培等[12]在偏好泊位约束下，研究了泊位和岸桥的集成分派问题，随后谢鑫等[13]假设船舶抵港时间具有固定的时间间隔，进一步研究了离散泊位环境下船舶抵港时间和装卸时间的随机波动分析。然而连续泊位下船舶抵港时间和装卸时间的随机波动性分析却很少被学者研究。

本文以船舶抵港时间和装卸时间的随机波动作为出发点，考虑连续泊位上船舶离港延时惩罚、偏好泊位的影响，以最小化船舶总在港时间为目标，研究连续泊位环境下不同幅度的随机波动对船舶总在港时间的影响。

1 问题描述与假设

通常情况下，船舶抵港后码头调度员将根据码头的实际情况和调度策略将泊位和岸桥分配给船舶。泊位—岸桥的优化是指通过分配恰当的泊位、选择适当的靠泊顺序并配备合适的岸桥数，使船舶总在港时间较短，以提高码头利用率和客户满意度，并降低码头作业成本。本文考虑的泊位—岸桥分配问题为动态的、连续的，只要船舶条件满足靠泊的岸线长度，船舶便可沿连续岸线靠泊，多只船可以同时靠泊接受服务。本文提出的目标函数包含了两个方面的因素：①对船东而言，希望到港船舶被分配到理想的偏好泊位且处理时间延误最小；②对码头管理人员而言，希望停靠到码头的船舶数量和集装箱吞吐量能达到最大。当船舶靠泊后，实际占用的泊位单元数取决于船长，而占用的时间取决于岸桥装卸处理时间。本文将岸线视为连续的泊位，考虑船舶偏好泊位的影响以及船舶离港延迟惩罚的约束，以最小化船舶总在港时间为目标，建立的连续泊位和岸桥的集成分配模型将基于以下合理假设：

①每条船必须被服务且被服务一次，即不考虑移泊作业；

②处理时间由所在泊位、岸桥数量决定，不考虑船舶的距离、集装箱运输等其他因素；

③泊位资源视为连续性的，被划分为尽可能多且相等的微小停泊单元，多只船舶可以同时停靠；

④每条船舶定义有同时作业的最大岸桥数与最小岸桥数，只有当可用岸桥数不小于最小岸桥数时方能开始作业，并且不能大于最大岸桥数；

⑤分散的闲置岸桥不能横跨工作，岸桥只能在岸线固定的位置为靠泊的船进行装卸；

⑥每条船舶定义一个最优偏好停靠位置，偏离偏好泊位会增加船舶总在港时间；

⑦假定靠泊计划在零时刻开始，所有船舶只有到港后才能靠泊作业，正常情况下靠泊后即可开展装卸作业。

此外，船舶靠港作业过程中的靠泊时间和离泊时间对于不同船型差异不大，且相对整个在港时间很小，在此忽略不计。

2 模型建立

2.1 相关概念和符号

B: 泊位岸线总长度；

BE: 岸线被等分的总数；

T: 计划期时长；

V: 计划期内的到港船舶集；

C: 港口总的岸桥数；

fk: 船舶k的延误惩罚；

bi: 泊位单元i的起点；

ti: 对应于泊位单元i的可用时间起点；

hk: 船舶k的长度(包括水平安全预留长度)；

lk: 可分配船舶k所需要的最少岸桥数；

uk: 可分配船舶k所需要的最大岸桥数，受船长的限制；

gk: 船舶k的总的岸桥作业时间 ，即船上集装箱装卸总时间，以单位桥时计算；

Sk: 船舶k的偏好泊位位置；

M:一个无穷大的正数。

决策变量：

xk: 船舶k靠泊的计划位置；

yk: 船舶k靠泊的计划时间；

Xkj: 船舶k在j时间段进行靠泊装卸作业时值为1，否则为0；

Ykj: 船舶k在j时间段被分配的岸桥数；

wbk：船舶k在锚地等待靠泊时间；

wck：船舶k在泊位等待岸桥时间；

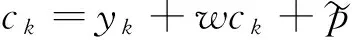
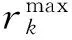
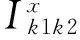
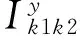
2.2 连续泊位和岸桥集成分配模型

目标函数:

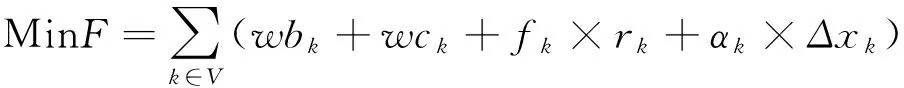
(1)

约束:

在小学数学教学的过程中，习题练习能够有效地帮助学生巩固知识记忆，同时也能够帮助教师了解学生的学习难点，从而能够有针对性地进行讲解。而在此过程中，教师也可以结合微课教学视频开展复习工作，提升学生的学习效率。

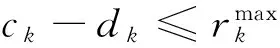
(2)

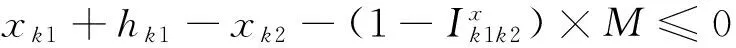
(3)

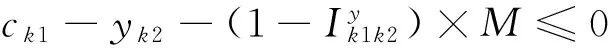
(4)

(5)

(6)

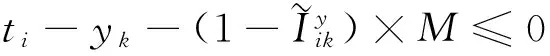
(7)

(8)

(9)

0≤xk+hk≤B∀k∈V，

(10)

(11)

(12)

(13)

Xkj≤Ykj∀k∈V,∀j∈T，

(14)

Ykj≤M×Xkj∀k∈V,∀j∈T，

(15)

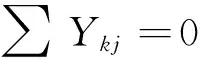
(16)

Ykj+M(1-Xkj)≥lk∀k∈V,∀j∈T，

(17)

Ykj≤uk∀k∈V,∀j∈T，

(18)

1≤yk≤T∀k∈V，

(19)

ek≥0,rk≥0∀k∈V，

(20)

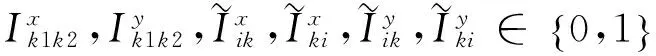
(21)

其中：式(1)是目标函数，最小化的船舶总在港时间由三个部分组成，第一部分是总的在港停留时间，包括船舶等待靠泊的时间和靠泊后的服务时间；第二部分是延误惩罚的时间成本，其中rk表示的是船舶k的离港延误时间；第三部分是偏离偏好泊位的时间成本，偏离距离越远，越影响装卸时间；这个目标函数旨在平衡码头和船公司双方的利益。式(2)中要求船舶离港时间必须在能接受的范围内，并且在港停留时间大于等待靠泊时间。式(3)和(4)定义了相邻两船的停靠位置、停靠时间。式(5)和(6)定义了待分配船舶与已分配船舶在停靠位置上的关系。式(7)和(8)定义了待分配的船舶与已分配船舶在停靠时间上的关系。式(9)保证待分配的船舶与已分配的船舶在停靠位置与时间上不发生冲突。式(10)是对船舶的停泊位置的限制。式(11)和(12)表示与偏好泊位的偏差距离。式(13)表示岸桥资源的限制不超过岸桥集总数。式(14)和(15)确定船舶在某一时间段是否有岸桥进行作业。式(16)表示在船舶靠泊之前的岸桥服务总时长为0。式(17)和(18)表示在某一时间段服务船舶的岸桥数量的限制。式(19)保证每只船不超过计划期限制；式(20)是保证其为非负且装卸完成之后必须离开；式(21)定义了六个0-1变量。

3 基于阶段的邻域搜索算法

邻域搜索算法的基本思想是在搜索过程中系统地改变邻域结构集来拓展搜索范围,获得局部最优解,然后在基于此局部最优解重新系统地改变邻域结构集拓展搜索范围找到另一个局部最优解的过程。由于邻域搜索算法具有实用性、有效性、时效性及鲁棒性的属性特点，本文将采用邻域搜索算法求解，算法具体分为以下三个阶段。

基本流程如下：

阶段一：初始化船舶序列(π)

步骤1根据船舶的预计到达时间初始化船舶序列(π)。

步骤2对于每个邻域结构，产生新的邻域船舶序列π′。

步骤3 对于邻域船舶序列π′，通过U(0,sps)对应产生一个相对靠泊位置的矢量(rBv)。

阶段二：确定船舶的靠泊位置

步骤4 根据相对前一个船舶或泊位开端的偏移量(rBv)一个接一个地设置当前船舶靠泊位置，从而确定序列π′ 中船舶的靠泊位置(rBv)。

阶段三：调整分配岸桥个数和停泊的位置

步骤5 服从以下约束条件，将分配给每艘船舶的岸桥数量一个接一个地增加，该限制条件会推进其他船舶的停泊时间：①可分配当前船舶岸桥的上线；②总可用岸桥的上限。

步骤6 调整π′中每个船舶的靠泊位置。

步骤7 如果π′相对π更优，改进更新π←π′；如果迭代不到mp，转到步骤3。

步骤8 若迭代后占新邻域的比例等于mn则返回,否则转到步骤2。

4 算例实验与分析

本文在不考虑水深影响的基础上选取了岸线为1 200 m的连续泊位，吊桥总数为12和20艘船舶设计算例，以评价和测试建立的模型。船舶的靠泊计划数据如表1所示。

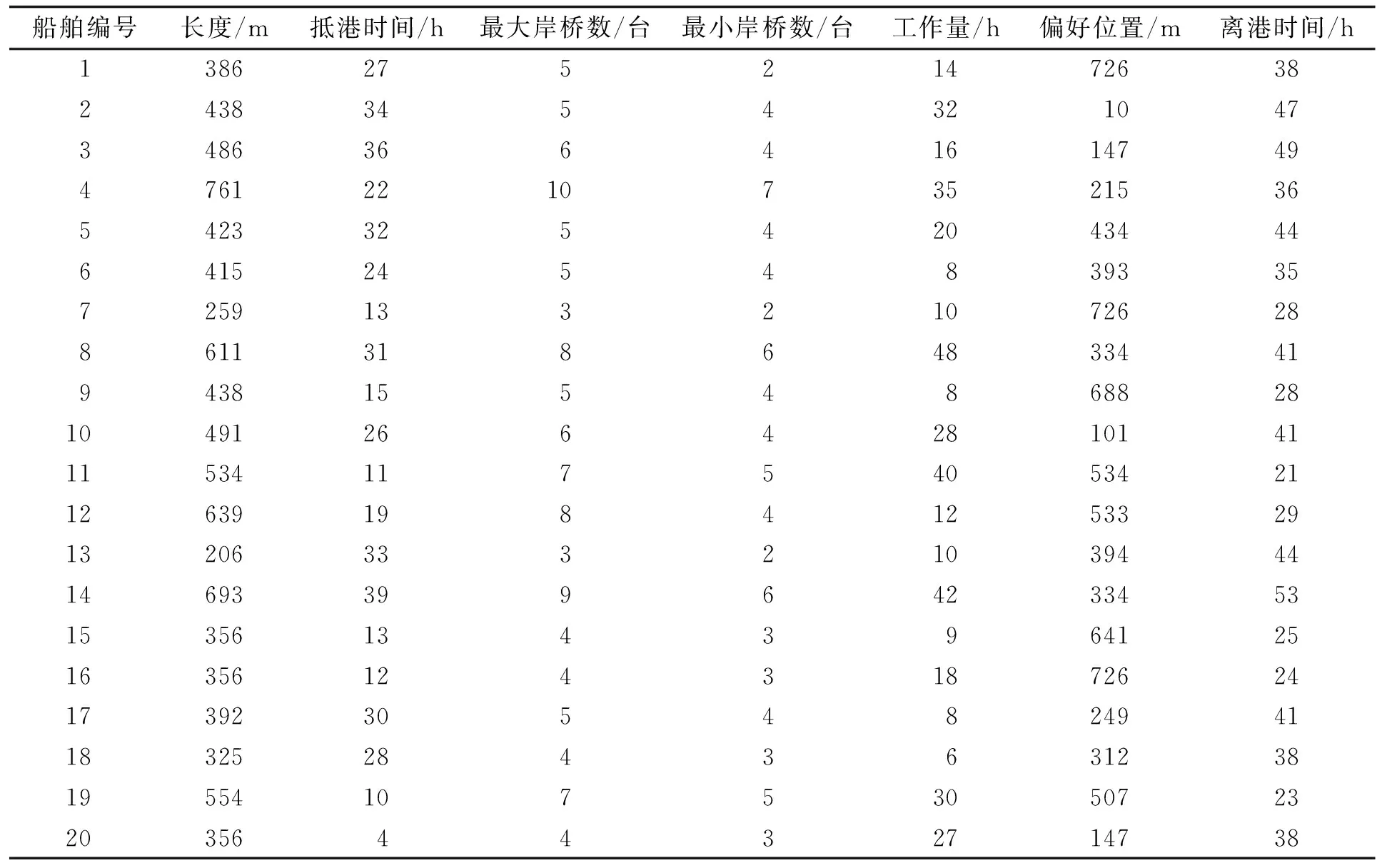
表1 船舶的靠泊计划数据

注：抵港时间、离港时间为预计时间，船舶装卸工作量的计量单位为桥时。

本文根据算例中的20条船舶计划抵港时间、计划离港时间、偏好泊位等参数，以邻域搜索算法求得船舶总在港时间最小的计划目标值F(F=85.9 h)，相应的船舶靠泊作业计划如图1所示。

船舶i[j]表示算例数据中编号为i的船舶分配j个岸桥

由于船舶航行速度、天气原因、岸桥机械故障等外部因素可能会造成船舶抵港时间和装卸时间在计划时间上产生随机波动。因此，需要考虑该部分因素对模型造成的影响。根据统计分析[13]，船舶抵港和装卸的实际时间与相应计划时间的偏差服从正态分布N(0,σ2)，本文在总在港时间最小的计划目标下，为偏差量设定不同的均方差代表外部环境对于计划时间产生的波动影响。根据波动幅度的大小随机生成σ2，在轻度波动下的在区间[1,2]上取值，中度波动下在区间[2,3]上取值，高度波动下在区间[3,4]上取值。

在船舶装卸时间不变的情况下，首先对抵港时间的计划值进行不同波动幅度下的随机处理，即计划抵港时间与偏差的和作为实际抵港时间。图2为抵港时间不同随机波动幅度下，计划目标值和3种抵港时间波动模式下的目标值及偏差幅度。分析图2可以得出，船舶总在港时间在轻度波动后，总在港时间从计划目标值的85.9 h下降至84.1 h，中度波动后继续下降至83.2 h。但在重度波动后，总在港时间没有继续下降，甚至略微增加至83.3 h。从算例中可以发现，这是符合港口作业实际情况的，一些船舶在同一时间或相近的时间抵港，抵港时间波动变大，使得单位时间内抵港的船舶变少，码头的泊位资源和装卸资源变得相对充裕，从而加快了船舶的作业效率，降低了船舶总在港时间。但在重度波动下，虽然单位时间内抵港的船舶更少，但每条船都有最大工作桥吊数的限制，泊位资源和装卸资源虽然更加充裕但并不能充分利用起来，因此总在港时间也不会因此继续降低。

然后在船舶抵港时间不变的情况下，对船舶装卸时间的计划值进行不同波动幅度下的随机处理，即计划装卸时间与偏差的和作为实际装卸时间。图3为装卸时间在不同的随机波动幅度下，计划目标值和3种波动幅度下的目标值及偏差幅度。分析图3可以得出，船舶总在港时间随着随机波动的扩大，目标值从计划的85.9 h一直上升至重度波动下的128.8 h，并且偏差率也随之增大。这是由于当计划抵港时间产生随机波动时，码头的总体靠泊计划可以随之进行优化调整，而当船舶已经抵港的情况下，由于不确定原因导致的装卸时间波动，即使后续进行优化调整也必然会挤占船舶总在港时间，波动越大，影响越大。

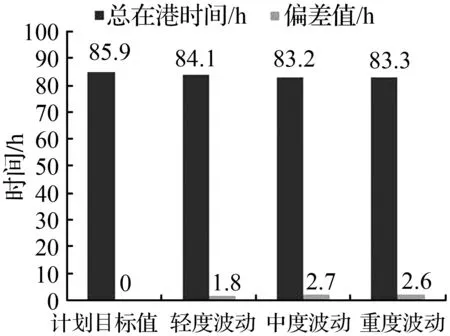
图2 抵港时间波动

Fig.2 The fluctuation of arrival time

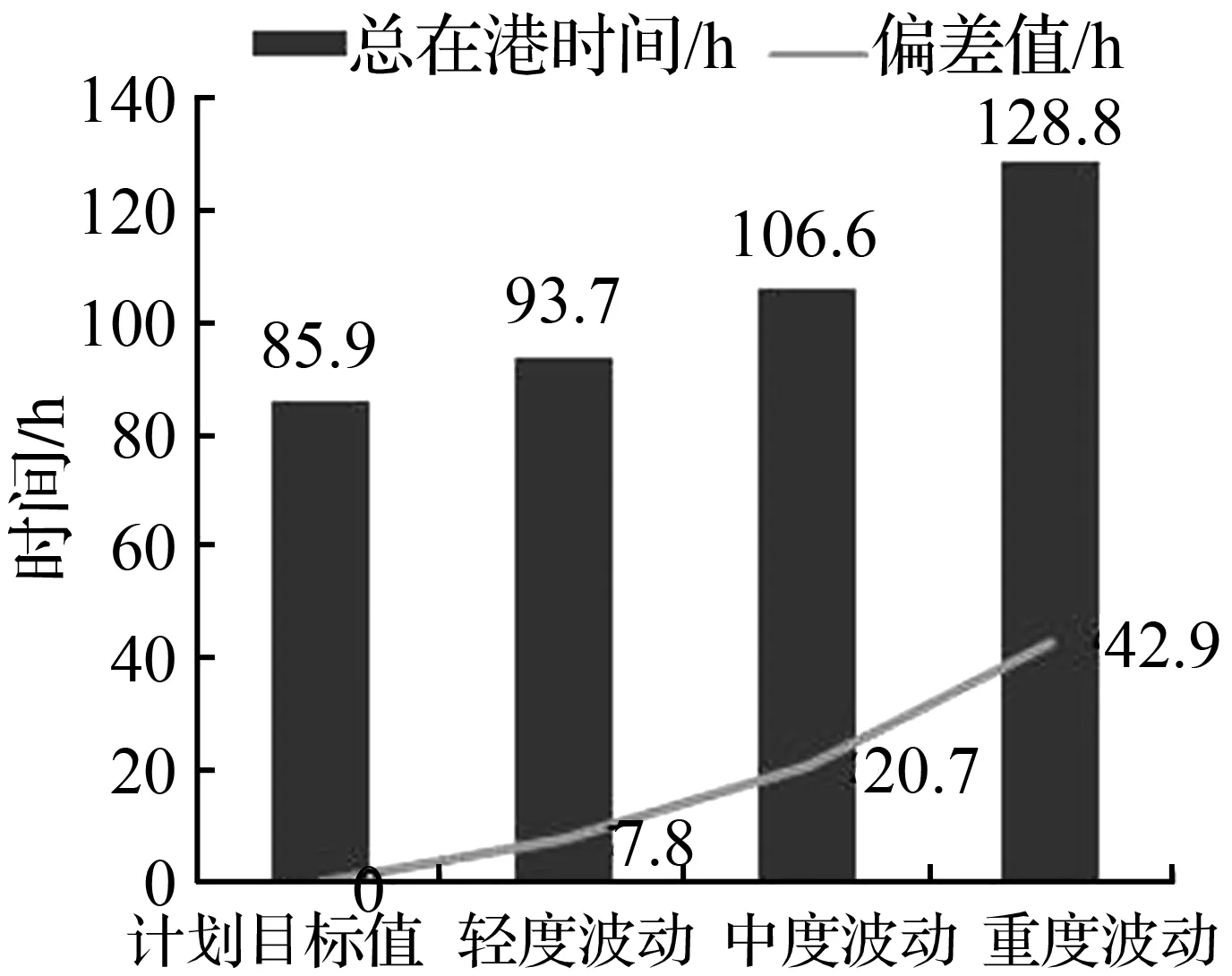
图3 装卸时间波动

Fig.3 The fluctuation of handling time

从上图2和图3的对比分析中可以发现，由于装卸时间波动产生的目标值相比于计划值的偏差要远大于由于抵港时间波动所产生的偏差。在集装箱码头连续泊位的作业过程中，以抵港时间变动为依据调整船舶靠泊计划会产生较好的效果。

5 结 论

本文考虑船舶的实际抵港与装卸时间具有一定幅度的随机波动，建立连续泊位和岸桥的集成分配模型，以最小化船舶总在港时间为目标，采用基于邻域搜索的重调度算法对模型进行了求解。然后在最优解的基础上对抵港和装卸时间做随机波动处理，分析了其对整体靠泊计划的影响，为靠泊计划的动态调整提供理论参考。实验结果显示，当抵港时间发生波动时，对船舶靠泊计划影响较小，最大偏差值为2.7 h；而当装卸时间发生波动时，对船舶靠泊计划影响较大，最大偏差值为42.9 h。因此，由装卸时间波动导致的船舶总在港时间偏差远大于由抵港时间波动导致的偏差，靠泊计划的动态调整优先考虑抵港时间的变化。

此外，本文还存在一些不足，所建模型中目标函数的评价指标单一，只考虑了时间的随机性等。制定有效的缓冲时间，在保证港口正常作业的基础上，最大程度的减小船舶实际抵港和装卸时间波动产生的影响是本文后续研究的方向。

[1] BARROS V H, COSTA T S, OLIVEIRA A C M, et al.Model and heuristic for berth allocation in tidal bulk ports with stock level constraints[J]. Computers & Industrial Engineering, 2011, 60(4):606-613.

[2] 乐美龙, 刘菲.基于Memetic算法的泊位和岸桥分配问题[J]. 武汉理工大学学报, 2011,20(11):66-71.

[3] IMAI A, NISHIMURA E, PAPADIMITRIOU S.Berth allocation with service priority[J]. Transportation Research Part B Methodological, 2003, 37(5):437-457.

[4] IMAI A, SUN X, NISHIMURA E, et al.Berth allocation in a container port: using a continuous location space approach[J]. Transportation Research Part B Methodological, 2005, 39(3):199-221.

[5] MEISEL F, BIERWIRTH C.Integration of berth allocation and crane assignment to improve the resource utilization at a seaport container terminal[J]. Operations Research Proceedings, 2005, 26(4):105-110.

[6] LIANG C, HUANG Y, YANG Y.A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning[J]. Computers & Industrial Engineering, 2009, 56(3):1021-1028.

[7] 乐美龙, 刘秀玲.基于泊位偏好与服务优先级的泊位和岸桥分配[J]. 辽宁工程技术大学学报(自然科学版), 2013,39(5):709-712.

[8] Kim, Hwan K, Chan K.Berth scheduling by simulated annealing[J]. Transportation Research Part B Methodological, 2003, 37(02):541-560.

[9] 赵坤强, 韩晓龙, 梁承姬.连续泊位下集装箱港口泊位与桥吊协同调度优化研究[J]. 武汉理工大学学报, 2011,20(11):60-65.

[10]MOORTHY R, TEO C P.Berth management in container terminal: the template design problem[J]. Operations Research-Spektrum, 2006, 28(28):495-518.

[11]曾庆成, 胡祥培, 杨忠振.集装箱码头泊位分配—装卸桥调度干扰管理模型[J]. 系统工程理论与实践, 2010, 30(11):2026-2035.

[12]蒋大培, 胡志华, 胡少龙.考虑偏好泊位的泊位和岸桥集成分派问题[J]. 广西大学学报(自然科学版), 2014,39(3):663-672.

[13]谢鑫, 胡志华.抵港和装卸时间不确定情况下的离散泊位分配问题[J]. 华中师范大学学报(自然科学版), 2014, 47(6):813-818.

(责任编辑 梁 健)

Research on integrated allocation of continuous berth and quay crane under stochastic environment

HAO Yang-yang， LIU Tian-ci, HUANG You-fang

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

Berth and quay are the most important resources in container ports, it’s allocated and scheduled optimally under stochastic environment can improve the ports’ efficiency. An integrated allocation model of continuous berth and quay crane under stochastic environment is proposed by considering the delay cost, preferred berthing position, and the aim to minimize the total time of shipping in ports. Then, a solution is done with a VC++ simulate program and a reschedule method based on neighborhood search heuristics. The results of experiment indicate that the maximum deviation of berthing plan was 2.7 h when the arrival time occurs fluctuation and the maximum deviation was 42.9 h when the service time occurs fluctuation. Thus the deviation of total time in ports produced by the fluctuations of service time is more obvious than that of the arrival time, and providing theory basis for ships berthing plan under uncertain environment which caused by the ship’s arrival and handling.

stochastic environment; berth-quay crane; continuous berth; p

berth; neighborhood search

2016-04-10；

2016-07-06

国家自然科学基金资助项目(71301101)；交通运输部建设科技项目(2015328810160);上海自然科学基金项目(15ZR1420200)；教育部人文社科项目(15YJC630059)

黄有方(1959—)，男，上海人，上海海事大学教授，博士生导师，博士；E-mail：yhuang@shmtu.edu.cn。

郝杨杨，刘天赐，黄有方.随机环境下连续泊位和岸桥集成分配问题研究[J].广西大学学报(自然科学版)，2016，41(5)：1457-1464.

10.13624/j.cnki.issn.1001-7445.2016.1457

TP18

A

1001-7445(2016)05-1457-08