基于复杂网络的全球海运网络鲁棒性研究

刘婵娟，胡志华

(上海海事大学物流研究中心， 上海201306)



基于复杂网络的全球海运网络鲁棒性研究

刘婵娟，胡志华

(上海海事大学物流研究中心， 上海201306)

为研究全球集装箱海运网络鲁棒性，了解全球集装箱海运网络抗干扰能力，根据2015年全球最新10大集装箱班轮运输公司中的7家公司的航运数据构建了全球集装箱海运网络。运用复杂网络理论和方法测算其拓扑结构特征，设计随机干扰和蓄意攻击两种仿真系统，从连通鲁棒性和功能鲁棒性两个角度展开研究。仿真实验结果表明：全球集装箱海运网络针对随机干扰具有较强的鲁棒性，而在蓄意攻击下鲁棒性较差；不同港口对网络鲁棒性的影响差异较大，通过仿真分析分别得到了对全球集装箱海运网络连通鲁棒性和功能鲁棒性影响最大的10个港口，这些港口大多是亚洲港口，其中上海洋山港对全球海运网络连通鲁棒性和功能鲁棒性都具有较大的影响。研究结果可为全球集装箱海运网络重要港口的保护提供参考。

国际物流；海运网络；复杂网络；鲁棒性；仿真

0 引 言

分析全球集装箱海运网络的鲁棒性，可以帮助识别海运网络中的重要港口，为全球集装箱海运网络优化提供依据，保证海上运输的安全高效。

对于鲁棒性的概念专家们有不同的定义。Gribble[1]认为“一个系统能够在一系列不同的操作条件下继续正确运行，且其在这些条件之外发生故障的概率很低，那么它就具有一定的鲁棒性”。Alis等[2]从资源分配的角度讨论了鲁棒性。他们认为如果一个资源分配的方案在其组成部分行为或周围环境有所波动下仍能保证维持某些系统所需特性，那么这个分配方案具有鲁棒性。

已经有很多学者研究控制系统鲁棒性[3-4]。近年来国内外很多学者开始关注交通网络鲁棒性的研究。Sakakibara等[5]提出了交通网络的机构布局指数的概念，他认为当每个节点上的链节数量都呈现出分散态势时，交通网络具有鲁棒性。Scott等[6]通过分析移除某些网络成员后整个网络的成本增加来检验交通运输网络的鲁棒性。文献[7-8]都通过仿真实验分析中国航空网络鲁棒性特征。文献[9-12]是对城市公交网络鲁棒性的研究。武佩剑等[13]通过对全球航运网络中部分节点进行删除后网络聚集系数、平均距离、孤立节点比率变化来分析全球航运网络鲁棒性和脆弱性。

然而，目前在交通网络鲁棒性研究中对全球海运网络鲁棒性的研究甚少，且研究内容主要是针对网络拓扑结构和连通性分析。本文从全球集装箱海运网络连通鲁棒性和功能鲁棒性两个角度展开研究，以期更加全面的揭示全球集装箱海运网络的鲁棒性特征。

1 全球集装箱海运网络拓扑结构

1.1 数据采集

为构建全球集装箱海运网络，搜集了2015年全球最新10大集装箱班轮公司中的7家公司(马士基、达飞、赫伯罗特、长荣、中远、中海和韩进)的航线数据，并以航运公司网站上的船期数据为基础，分别跟踪和获取每条航线上一个航期中班轮挂靠的所有港口，跟踪时间为2015年10月到2016年1月。统计得港口总数为777个，所涉及的航线总数为7 553条。

1.2 全球集装箱海运网络拓扑结构参数统计

全球集装箱海运网络可以被看做一个由港口和航线构成的无向无权网络。构建全球集装箱海运网络拓扑结构，如图1显示了度值排名前100个的港口拓扑结构。这些港口在海运网络中基本都处于枢纽位置，是海运网络中的基本港。

①度与度分布——一个节点i的度值k等于与它相连的节点数目。在全球集装箱海运网络中，当有较多航线经过某个港口，则说明该港口的度值较大。节点度分布函数P(k)，表示随机选择一个节点其度值为k的概率。

②平均最短路径——由于全球海运网络被看做无向无权网络，任意两节点i和j之间的最短路径所包含的边数等于这两个节点之间的距离dij。网络中所有节点对间的最短路径平均数等于整个网络的平均最短路径l，如式(1)所示,其中N为网络节点总数。

③聚集系数——网络中节点的聚集系数c表示该节点与其邻居节点之间连接的紧密程度。其计算公式如式(2)所示。式(2)中，设节点i的度为k，E(i)是节点i的邻居节点之间实际连接的边数,T(i)是节点i的k个邻居节点之间可能形成的最大连接数，其计算公式如式(3)所示。网络中所有节点聚集系数的平均值就是整个网络的聚集系数，如式(4)所示，其中N为所有节点总数。

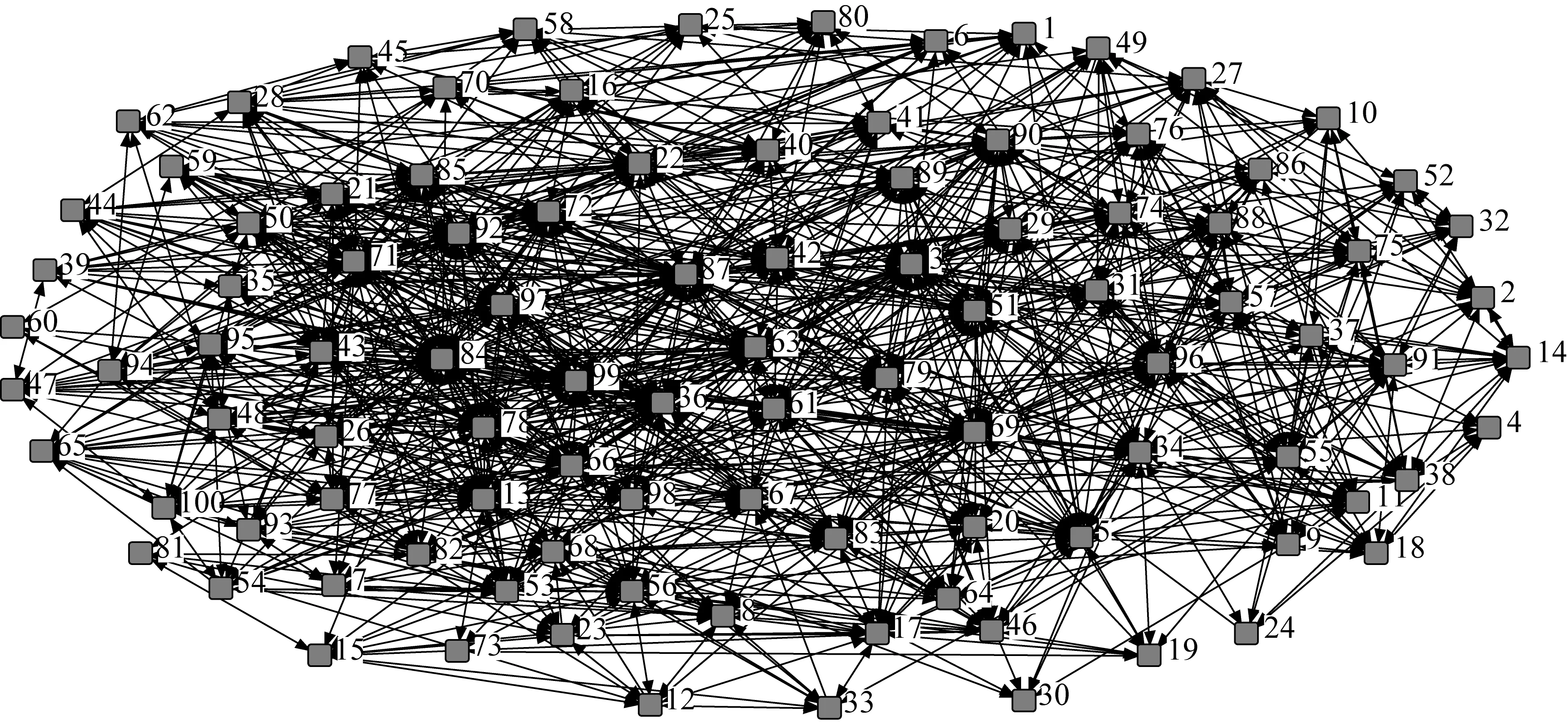
图1 度值前100港口网络拓扑结构

(1)

c(i)=E(i)/T(i),

(2)

T(i)=k(k-1)/2,

(3)

(4)

计算得全球集装箱海运网络平均最短路径约为3.263 3，任意两节点之间的最大距离为9，绝大多数小于5。整个网络聚集系数较大，为0.485 0，各港口度值及度分布曲线如图2和图3所示。从图2中可以看出，网络中节点度值最大为138，平均度值为9.720 7，说明在全球集装箱海运网络中经过任一港口的航线数平均约为10条。由图3可以看出，全球集装箱海运网络中节点度分布基本满足幂率分布，因此全球集装海运网络也具有无标度特性。

图2 海运网络各节点度值

Fig.2 Degree of each node in shipping network

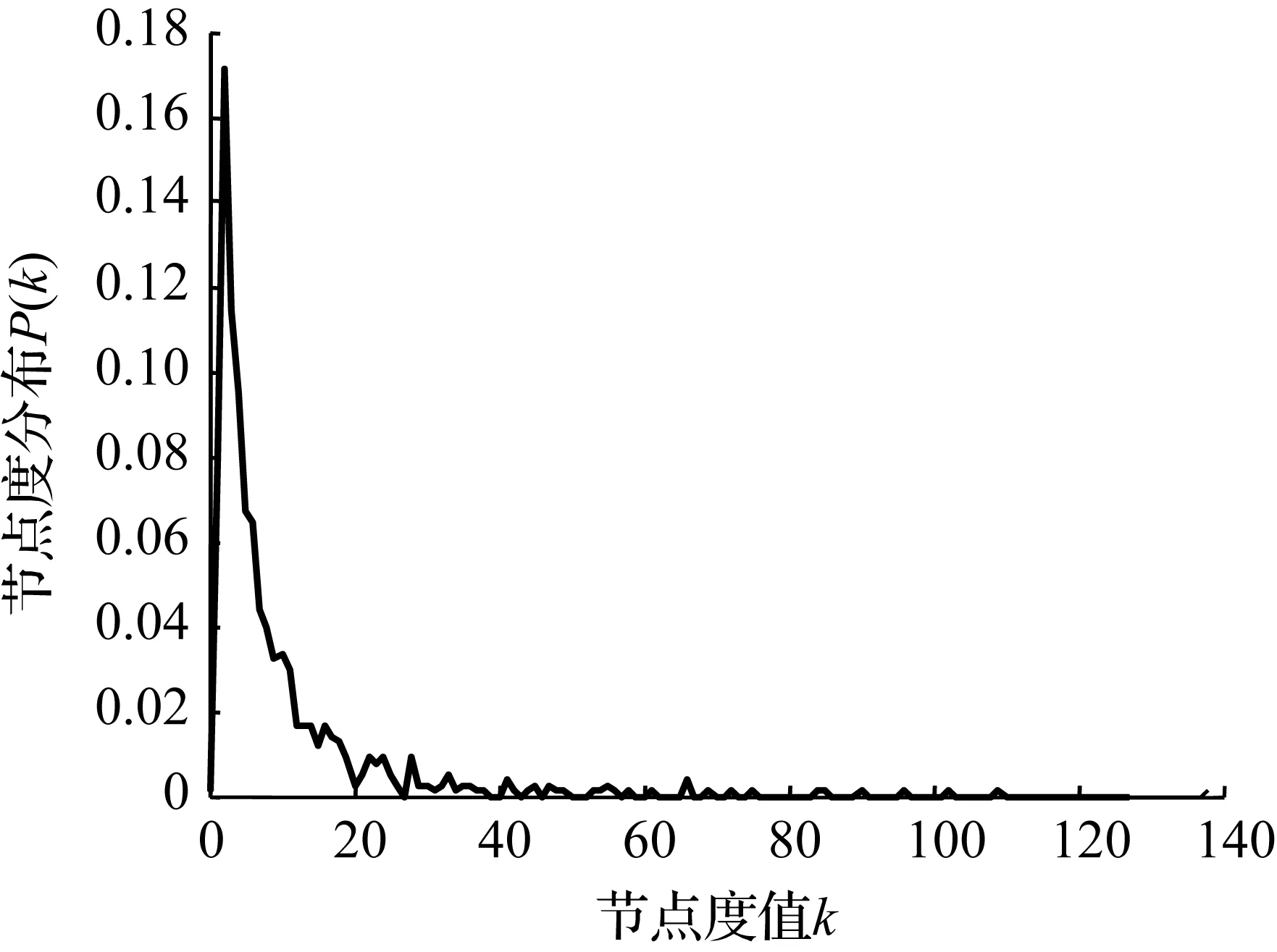
图3 海运网络节点度分布曲线

Fig.3 Degree distribution of the nodes in network

2 全球集装箱海运网络鲁棒性分析

2.1 全球集装箱海运网络鲁棒性度量标准

在全球集装箱海运网络中，由于自然灾害等因素的影响某些港口陷入瘫痪，那么与此港口相连的其他航线也将无法通航，这将导致海运网络中部分路径中断。如果部分港口被移走后海运网络中绝大多数节点仍然是连通的，则该集装箱海运网络对这些港口的故障就具有一定的鲁棒性。

本文以“被攻击节点数占原集装箱海运网络中节点总数的比例f”与“最大连通子图相对大小s”和“网络平均最短路径长度l”之间的关系来衡量集装箱海运网络的鲁棒性[14]。从连通鲁棒性和功能鲁棒性两个角度来研究全球集装箱海运网络鲁棒性特征。

①海运网络连通鲁棒性度量标准

用最大连通子图的相对大小s来衡量网络的连通鲁棒性，计算公式如式(5)所示。最大连通子图包含的节点数越大表示网络连通性越好，当其与网络总节点数相等时，表明所有节点间都是可以互联的。当f保持不变时，s越大，网络连通鲁棒性越好。

(5)

②海运网络功能鲁棒性度量标准

海运网络功能鲁棒性是指海运网络中的特定服务功能对去除某些节点的阻抗程度。根据文献[15]的研究，将网络平均最短路径长度达到最大值时的fc作为整个网络功能鲁棒性的度量指标，如式(6)所示。fc越大说明此时网络功能鲁棒性越差，而当f保持不变时，l越大，其对应的被攻击节点对网络功能鲁棒性影响越大。

fc={f|网络平均路径长度达到峰值}。

(6)

2.2 全球集装箱海运网络鲁棒性仿真系统设计

根据集装箱海运网络连通鲁棒性和功能鲁棒性衡量标准，本文应用MATLAB软件，设计随机攻击和蓄意攻击两种攻击策略来对全球集装箱海运网络的鲁棒性进行仿真实验。鲁棒性仿真实验流程见图4。

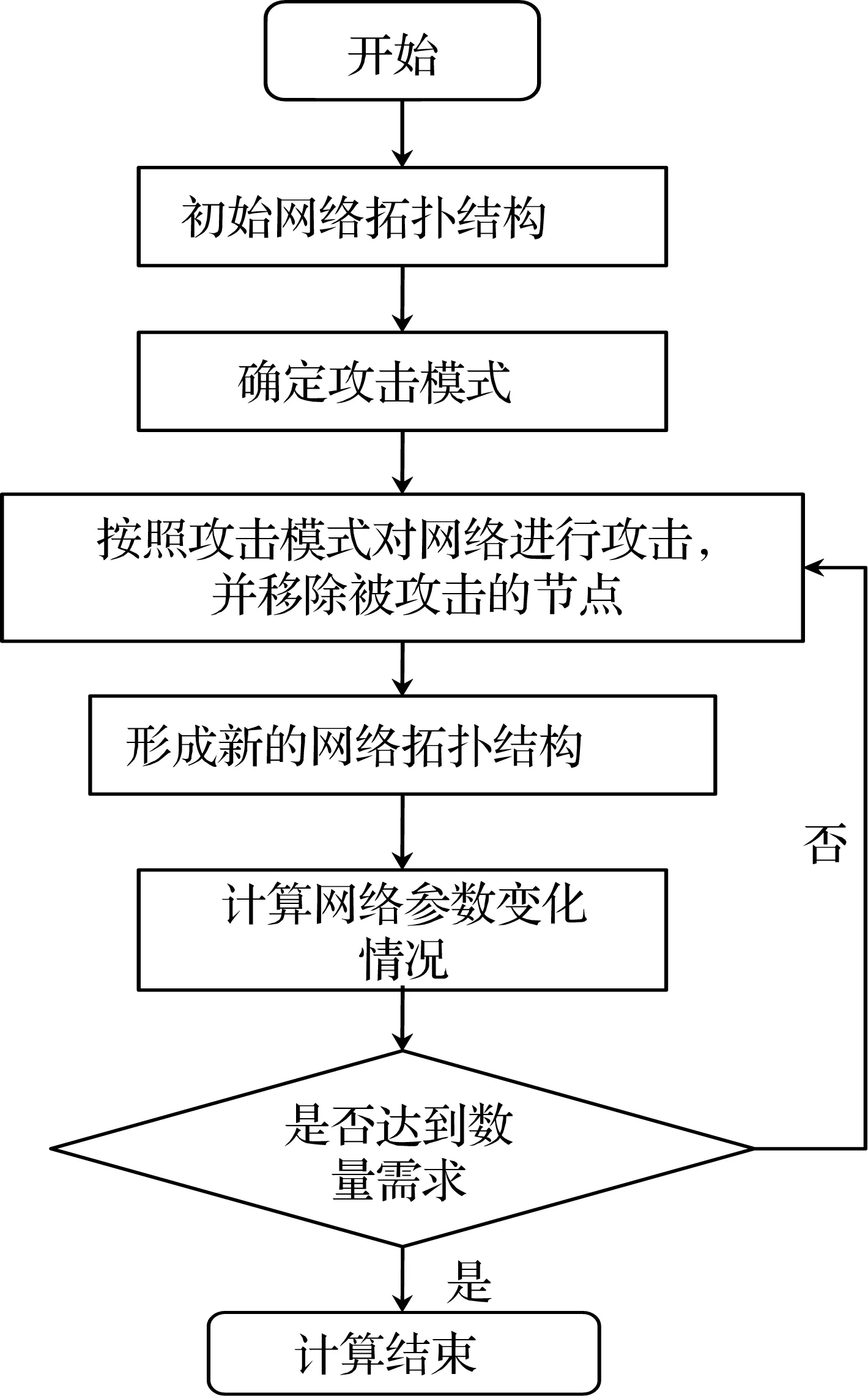
图4 海运网络鲁棒性仿真实验设计思路

随机攻击实验主要分析集装箱海运网络的连通鲁棒性。在随机攻击中，通过MATLAB生成随机数的方式确定被攻击节点，当某个节点被攻击时删除该节点以及与之相连的所有边，形成新的海运网络。蓄意攻击实验主要分析海运网络的功能鲁棒性。由于节点度数和聚类系数均是反映节点重要性的关键指标，因此本文综合这两项指标来确定集装箱海运网络被蓄意攻击的次序。采用节点度和聚集系数排名次序之和DC(degree and coeffient)作为反映港口重要性的评判指标，按照从小到大的次序排列，作为对集装箱海运网络中港口的蓄意攻击次序。部分节点DC值及排名见表1。由表1可知，台中、南沙、基隆、西哈努克、 克莱佩达、武海马尔、胡志明、哈尔迪亚、天津、纳霍德卡等港口在全球集装箱海运网络中具有重要地位。

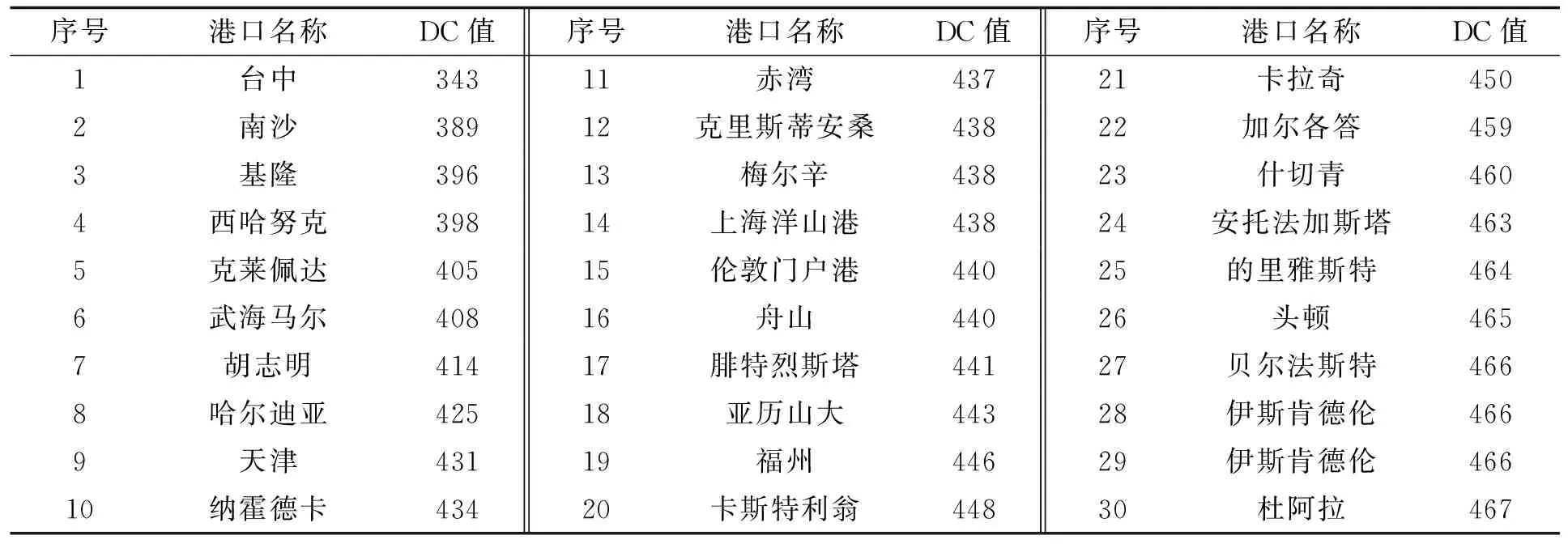
表1 部分节点DC值及排名

2.3 全球集装箱海运网络鲁棒性仿真分析

在随机攻击和蓄意攻击两种仿真系统中，以被攻击节点数逐渐增加的方式分别进行777次仿真实验，并记录每次仿真实验中f,s,l的值。分析全球集装箱海运网络在随机攻击和蓄意攻击策略下f和l以及f和s的关系，分别见图5(a)和(b)。

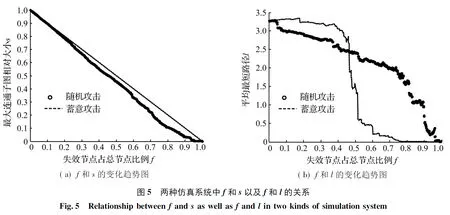
由图5(a)可知，在蓄意攻击下系统中s的下降速度显然快于随机攻击。在随机攻击系统中，网络最大连通子图相对大小几乎呈线性递减趋势，且只有当f很大时s才会趋近于零，这表明在天气、自然灾害等随机因素影响下，全球集装箱海运网络中只有当大部分港口同时遭受影响才会导致整个海运网络的瘫痪。故全球集装箱海运网络连通性面对随机攻击具有较强的鲁棒性。而相比之下，蓄意攻击对海运网路连通鲁棒性影响较大。

由图5(b)可知，在蓄意攻击系统中l值呈现先增加后减少的变化趋势，主要因为随着被攻击的港口数量不断增加，海运网络中相连接的港口随之减少，当所有港口都彼此孤立时，l值为0。在随机攻击中f的峰值fc1=0.019 33；蓄意攻击中f的峰值fc2=0.176 55；fc2>fc1，根据海运网络功能鲁棒性度量指标可知，蓄意攻击下对海运网络功能鲁棒性的影响比随机攻击对其鲁棒性的影响要大。在随机攻击系统中，当f<0.5时，l变化并不大，这说明随机攻击对海运网络的整体便利性影响较小；在蓄意攻击中，l先增加后快速下降，在后期l快速下降是因为随着网络中被攻击节点数增多网络功能快速丧失。

3 不同港口对全球海运网络鲁棒性的影响分析

通过仿真攻击实验还可以分析单个港口对全球集装箱海运网络鲁棒性的影响，在全球集装箱海运网络的邻接矩阵中删除某一港口节点以及与其相连的所有航线，得到新的海运网络邻接矩阵，计算新的网络邻接矩阵s和l的值。

采用节点度和聚集系数排名次序之和DC(degree and coeffient)，作为反映港口重要性的评判指标。根据表1，选择DC值排名前20的港口依次进行攻击，得到删除部分核心港口后海运网络的s和l值见表2。由于对单个节点进行攻击，所得新网络的最大联通子图相对大小s的值基本保持不变，所以将新网络平均最短路径变化表示在图6中。

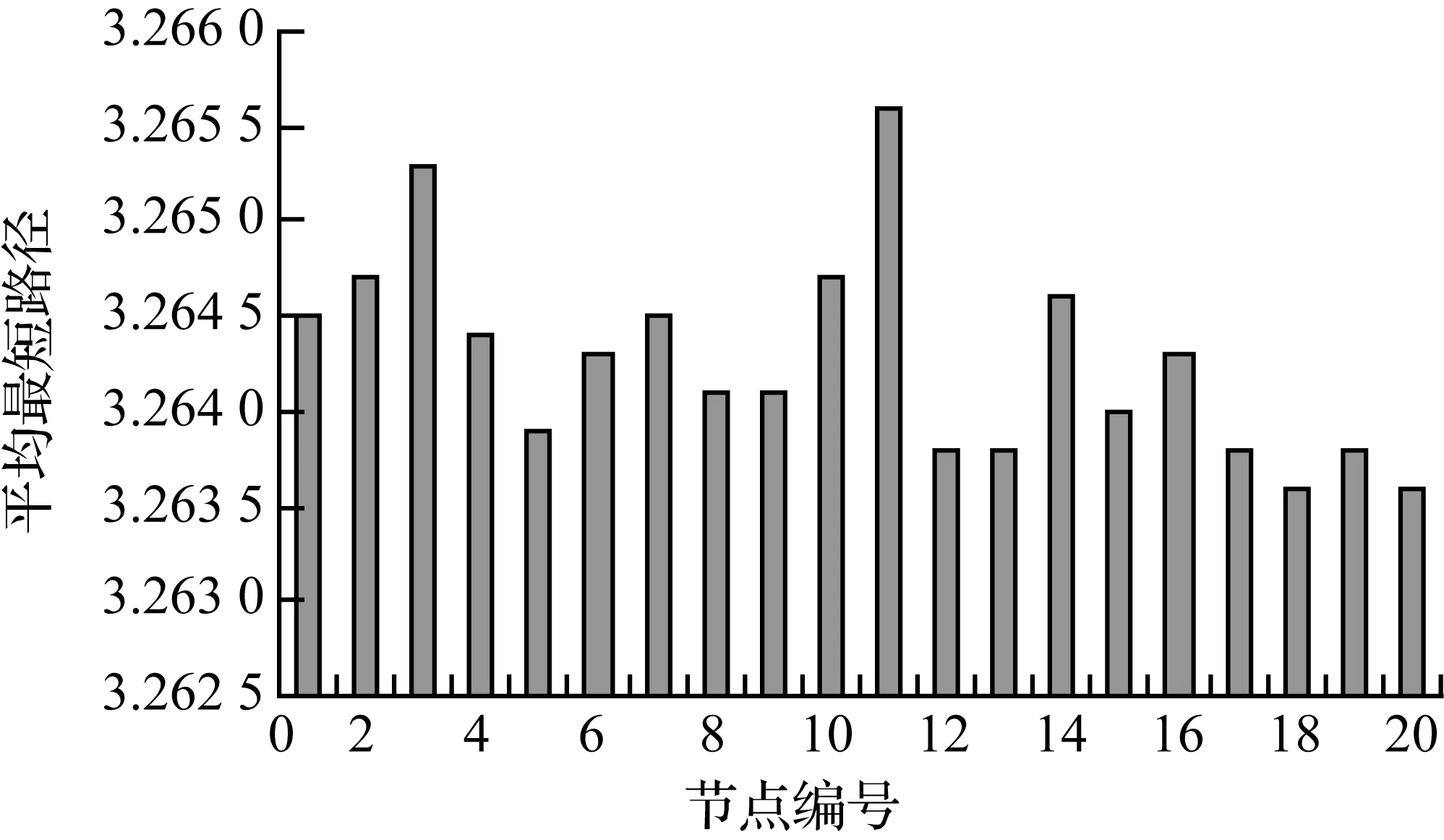
图6 删除部分核心港口后海运网络的平均最短路径长度l值

Fig.6 Value of the network’s average shortest pathlafter deleting the core ports

由图6和表2可知，从网络平均最短路径来看，对DC值排名前20的港口进行攻击后所得新的海运网络中，赤湾、基隆、南沙、纳霍德卡港、上海洋山港、台北、胡志明、西哈努克、武海马尔、舟山依次是新网络l越小的港口，表明这些港口在提高整个海运网络便利性方面发挥着极其重要的作用。

而最大连通子图相对大小s值都相等均为0.998 7。故按照度值从大到小的顺序依次删除节点求出各个新网络中最大连通子图相对大小s值，表3中列出了对应最大连通子图相对大小s值最小的前20个港口。

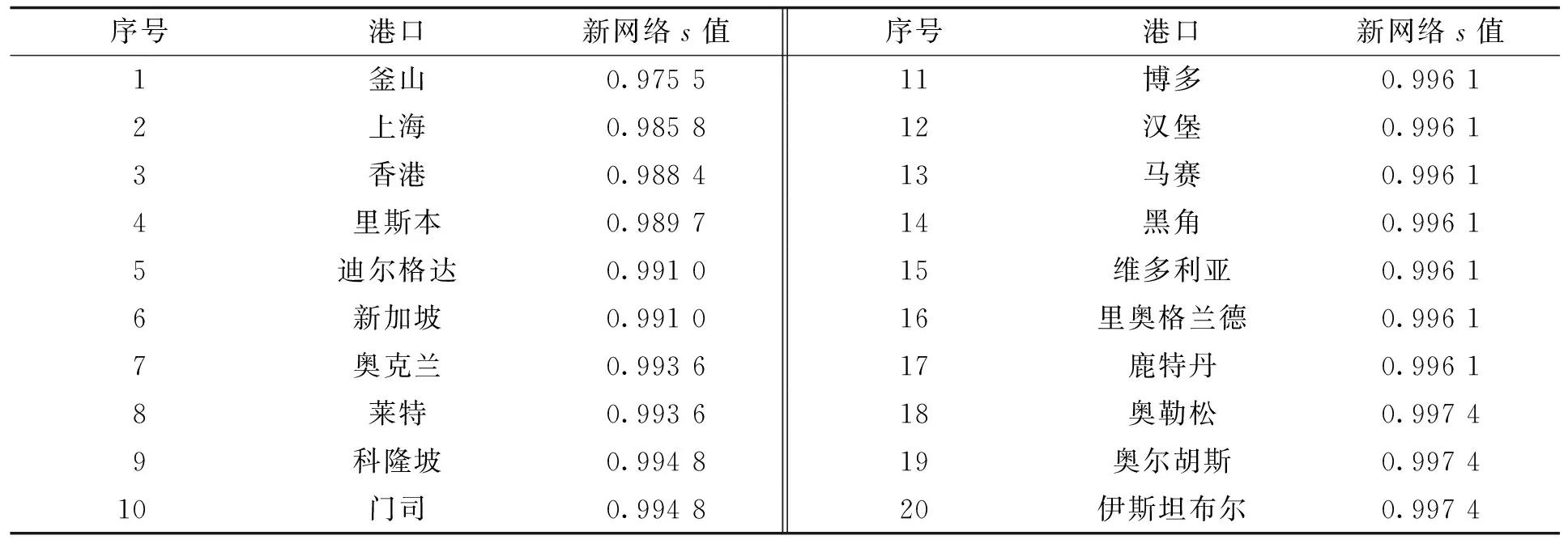
表3 攻击单个港口所得新网络最大连通子图相对大小s的值

由表3可知，釜山、上海洋山港、香港、里斯本、迪尔格达、新加坡、奥克兰、莱城、科隆坡、门司港，这10个港口s值最小，表明其在海运网络中具有沟通桥梁作用，他们对全球集装箱海运网络连通鲁棒性影响最大。对全球集装箱海运网络连通鲁棒性和功能鲁棒性影响最大的20个港口地理位置分布如图7所示。

图7 对海运网络连通鲁棒性和功能鲁棒性影响最大的港口地理位置分布

由图7可知，对全球集装箱海运网络连通鲁棒性和功能鲁棒性影响最大的港口均集中分布在亚洲、欧洲、非洲和大洋洲，其中约有二分之一的港口都是亚洲港口。并且上海洋山港不论是从连通性和功能性角度来说，都是对整个海运网络鲁棒性影响较大的港口。

4 结 论

从网络连通鲁棒性和功能鲁棒性两个角度研究了全球集装箱海运网络的鲁棒性，仿真实验结果表明全球集装箱海运网络面对天气、自然灾害等随机因素具有较强的鲁棒性，而在蓄意攻击下则比较脆弱。本文综合考虑网络中节点度和聚集系数两项指标来衡量节点重要性，并且通过仿真实验研究了单个港口对整个海运网络鲁棒性的影响。赤湾、基隆、南沙、纳霍德卡港、洋山、台中、胡志明、西哈努克、武海马尔、舟山依次是对全球集装箱海运网络功能鲁棒性影响最大的10个港口；门司、科伦坡、莱城、奥克兰、新加坡、迪尔格达、里斯本、香港、上海、釜山依次是对全球集装箱海运网络连通鲁棒性影响最大的10个港口。并且，对全球集装箱海运网络连通鲁棒性和功能鲁棒性影响最大的港口主要是亚洲港口；上海洋山港不论是从连通性和功能性角度来说，都是对整个海运网络鲁棒性影响较大的港口。

[1] GRIBBLE S D.Robustness in complex systems[J]. Proceeding Systems,2001, 3(5): 21-26.

[2] ALIS S, MACIEJEWSKI A A, SIEGEL H J, et al. Definition of a robustness metric for resource allocation[J]. Parallel and Distribution Processing Symposiun, 2003, 42(20): 1-10.

[3] 宫玉荣.基于模糊数学的控制系统鲁棒性分析模型仿真[J]. 科技通报, 2016, 32(2): 10-14.

[4] 王海龙.一类时滞不确定Lurie系统的鲁邦控制[J]. 广西大学学报(自然科学版), 2006, 31(2): 128-130.

[5] SAKAKIBARA H, KAJITAN Y, OKADA N.Road network robustness for avoiding functional isolation in disasters[J]. Journal of Transportation Engineering, 2004, 130(5): 560-567.

[6] SCOTT D, NOVAK D, AULTMAN H, et al. A new method for riden-tifying critical links and evaluating the performance of transportation networks[J]. Journal of Transport Geography, 2006, 14(3): 215-227.

[7] 姚红光,朱丽萍.基于仿真分析的中国航空网络鲁棒性研究[J]. 武汉理工大学学报, 2012, 36(1): 42-46.

[8] 张雯雯.复杂网络理论在航空网络中的应用研究[D]. 北京：中国民航大学, 2009.

[9] BERCHE B, VON FERBER C, HOLOCATCH T, et al.Resilience of public transport networks against attacks[J]. The European Physical Journal B, 2009, 71(1): 125-137.

[10]VON FEBER C, HOLOVATCH T, HOLOVATCH Y, et al.Attack vulnerability of public transport networks[J]. Traffic and Granular Flow, 2007, 20(13): 721-731.

[11]WU J J, GAO Z Y, SUN H J.Urban transit system as a scale-free network[J]. Modern Physics Letters B, 2004,18(19): 1-7.

[12]段后利,李志恒,张毅.城市公交网络的鲁棒性分析模型[J]. 华南理工大学学报, 2010, 38(3): 70-75.

[13]武佩剑,邓贵仕,田炜.集装箱航运网络拓扑特性研究[J]. 武汉理工大学学报, 2008, 32(4): 665-668.

[14]高亮,李梦辉,吴金闪,等.食物网络在顶点攻击与边攻击下的鲁棒性[J]. 系统工程理论与实践, 2005,7(15): 1-8.

[15]ALBERT R, BARABASIS L. Statistic mechanics of complex networks[J]. Review of Modern Physics, 2002, 74(2):47-97.

(责任编辑 梁 健)

Robustness research of global container shipping network based on complex network

LIU Cha-juan, HU Zhi-hua

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

In order to study the robustness of global container shipping network and to understand its anti-jamming ability, the world container shipping network topology structure was constructed based on the seven companies’ liner shipping data of the top 10 in the 2015. Complex network theory and method are used to calculate the parameter about shipping network’s topological structure. Both of connectivity robustness and function robustness are studied. Besides, two different attack methods are designed to research the network’s robustness. Simulation results show that global container shipping network has strong robustness under the random interference, and poor under intentional attack. The influence of different ports on network robustness is greatly different. Finally, the top 10 ports, which have biggest influence on the network’s connected robustness and function robustness, are determined respectively, most of these ports are in Asia. Besides, Yangshan port has great influence on the connectivity robustness of the global shipping network and function robustness. The research results provide reference for the protection of the important ports in the global container shipping network.

global logistics; shipping network; complex network; robustness; simulation

2016-06-26；

2016-07-21

国家自然科学基金青年项目(71101088)；国家自然科学基金面上项目(71471109)；上海市曙光计划项目(13SG48)；交通部应用基础研究项目(2015329810260);2016年上海海事大学研究生创新基金项目(2016ycx021)

胡志华(1979—)，男，湖南长沙人，上海海事大学教授，博士生导师；E-mail：zhhu@shmtu.edu.cn。

刘婵娟，胡志华.基于复杂网络的全球海运网络鲁棒性研究[J].广西大学学报(自然科学版)，2016，41(5)：1441-1448.

10.13624/j.cnki.issn.1001-7445.2016.1441

C94

A

1001-7445(2016)05-1441-08