投资风险计量方法的阶段性特性分析
郭晓璐
投资风险计量方法的阶段性特性分析
郭晓璐
马克维茨的资产选择理论为采用均值—方差法来衡量投资风险奠定了基础,通过风险与收益的效用分析选择投资组合,然而随着市场的发展变化,该理论与投资分析产生了一定的矛盾。本文从投资风险以及一般统计学风险角度阐述了马科维兹风险计量方法存在的问题,并分析了相关原因,以建立更切合当前投资实际的期望-半方差风险计量模型。
投资风险 计量方法 阶段性
一、引言
近20年来国际金融市场的发展使行业内的竞争加剧,现代金融理论、金融工程技术和计算机技术的发展为金融投资带来了更多的可能性。目前关于投资风险的计量有很多指标,包括以投资收益率的方差、标准差为基础的计量方法;以Hurst指数计量的风险指标代表的非线性计算方法;以收益率的下方风险为基础的计量指标,包括Var、LPM等等。投资除了存在系统性的市场风险之外,主要面对的风险就是价格波动的风险,这种因为价格波动而带来损失的可能性就是我们所说的投资风险。运用统计学的方法对投资风险进行计量通常运用的是均值方差,用于指导投资者关注风险,把握投资时机。
二、投资风险概述
投资风险管理经历了60年代的资产负债模式到80年代的资本协议约束模式,到现代的全面风险管理模式,经过金融危机的洗礼,各国领导吸取经验教训,认识到金融危机中最大的教训就是监管责任的不到位,美国监管部门对于金融投资机构的管理有欠缺,因此诞生了新的衍生工具,从管理思想到风险管理定价模型到市场风险与信用风险的相关关系等内容确定了投资风险的测算和管理方法。通过一系列的模型定出最终收益与风险的相关关系,给出相应的评级,为投资者提供投资参考。市场定价模型考虑的因素包含市场的所有因素,例如基础资产、交易对手金融违约风险等,也为信用资产的归类给出了相关性指导。构建了风险管理的识别和量化体系,实施新资本协议的目标来指导提高风险管理水平。建立有效的风险评估模型,控制操作风险,运用巴塞尔规定的基本指标法和标准法以及高级计量法,对相关数据进行测量。
三、投资风险统计学特征
(一)偏差的好坏
当收益率波动向下时,低于投资者预期,就是一种坏的偏差,反之投资收益率向上波动,可能高于投资者预期时就是一种好的偏差,通常情况,对于多头投资者而言,投资风险就是坏的偏差。对于空头投资者而言则情况相反。观察收益率曲线的波动情况和总体走势能够帮助投资者对风险形成预期,以及判断市场情绪。
(二)投资风险的期望特性
对于投资者来说,投资风险与投资期望是相对的,当实际获得的投资收益高于投资者的原始期望值时,有利于投资者建立信心,与此同时,投资期望值越高,投资风险就越大,此时投资者将舍弃低盈利机会,增加融资,用于投资更高风险高收益的项目,其期望值也同时增加。因此,对于投资风险的分析一定是建立在投资期望的基础上的。通常投资都有一定的周期,根据投资周期的阶段性,能够运用统计学方法对投资风险进行计量,运用均值—方差量化投资者实际收益情况,通过统计分布情况分析投资的好坏。在投资实践中通常选择无风险收益率作为期望收益率,并且将低于无风险收益率的投资视为发生投资风险,若是针对个人投资者的研究则需要依据个人投资者的投资期望来进行测算。
(三)投资风险的时间特性
设定不同的统计周期对投资风险进行测量,其风险程度会有所差异。时间单位属于月、季、年以上的投资为长线投资,时间以日、周为单位为短线投资。投资风险的时间特性与不同时间段的投资收益相关联,因此描述投资风险时应当以时间为基础,叙述为月投资风险、季投资风险和年投资风险。
四、基于均值-方差模型的风险计量方法
均值—方差模型是统计学的基本计量方法,在马科维兹之后的研究集中于期望收益率曲线向下趋势的风险研究,并且建立了计量风险的通用公示:
定义:W为未来的财富值;
f(W)表示财富值的概率密度;
F(W)表示财富值的积累概率密度;
U表示财富的期望值;
得到的计算公示如下:
第四,财富值低于期望的概率
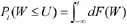
将以上公示进行合并得到如下公示:

将W固定于U上之后,得到专门用于计量Downside Risk的a-t两参数模型,也就是现在著名的LPM(Lower Partial Moments)模型:
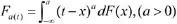
上述公示中的a,t可以代表任意值,通常情况只讨论a取值为0,1,2的情况;当a=0时,LPM0表示低于期望的概率水平;当a=1时,LPM1表示低于期望的收益率与期望值之间的偏差;当a=0时,LPM2表示低于期望的收益率与期望之差的平方的平均可能性。
五、期望-半方差风险计量模型
2000年之后学术界开始重新审视半方差的计量方法,并给出了一个新的计算方法,如表1所示:

表1 基于均值的半方差计算方法
半方差计量方法具有以下几个特点:
首先,半方差的运用并不常见,投资者对这种方法不熟悉。
其次,投资经理在实践中需要考虑投资成败问题,如果运用半方差计量需要承担较高的风险,一旦失败会带来相关法律问题。
再者,马科维兹凭借资产选择论开创了均值—方差的先河,并因此获得了诺贝尔经济学奖,因此对风险计量方法的革新造成了一定的阻碍。
最后,目前还没有基于半方差方法的投资模型,无法充分发挥半方差方法的优越性。
在Downside Risk的理念指导下,20世纪90年代经济学界提出了Vra(Value at Risk)的概念,并运用到投资风险计算当中。经过一段时间的组合与实践应用,将Var定义为在一定置信区间的损失最大可能性,其计算采用收益率的联合正态分布,在此基础上进行参数假设的设定。然而,Var存在较大的缺陷,主要表现在,只计算左尾尖的大小而非全部下行风险;只考虑了投资安全问题,没有考虑上行趋势带来收益的可能性,因此只适用于评估资本充足性。
六、两阶段计量方法检验
检验投资风险计量方法与现实情况是否相符,需要将模型测算的数据与实际情况进行对比。为此,本文选择了上证指数5年来的损失计算数据,统计了以周为周期的统计期间收益率的变化情况,以收益率低于无风险收益率的数据作为投资风险点,然后计算其差值再加上1,以此类推计算了50个交易周的几何平均值,得到了全年每周的损失可能性。(表2)

表2 用几何平均法计算的历年上证指数的每周可能损失方差计算结果
通过上述检验,SV值的每周可能损失相关系数为0.994,由此可以推断其风险表达效果,基本一致;每周可能损失值的方差相关性只有0.463,方差基本不能表达每周可能的损失。加入资本因素的半方差方法与计算可能损失值的几何均值方法,复杂程度相似,但是准确性有所差距。
七、结语
在测算投资风险的时候,应当把风险定义在收益率的均值偏差基础上,更能反映现实情况,根据投资风险的特性,通过改进半方差计量方法,加入资本因素,运用现代计算机技术,使计算结果更客观,计算方法更简洁,通过本文的讨论发现,几何均值的标准是最准确的检验方法。我国的无风险利率处在近20年以来的低位,投资风险较大,在进行投资组合与风险管理中要利用上述风险评估模型,进行合理有效的评估,同时有关部门应当合理引导投资机构,增加对投资机构的指导,以及对投资者的风险提示,改进净资本、风险资本准备计算公式,加强资本质量和风险计量的针对性;完善杠杆率指标,提高风险覆盖的完备性;强化全面风险管理要求,提升风险管理水平,从而促进投资市场的健康可持续发展,顺应我国经济发展的大潮流。
(作者单位为中海石油财务有限责任公司)
[1] 潘立生,杨晓.非效率投资计量模型有效性检验——基于经济周期阶段性研究[J].合肥工业大学学报(社会科学版),2014(1):9-17.
[2] 马晓梅,胡华.基于风险计量指标的投资组合模型及风险控制策略[J].通化师范学院学报,2014,35(8):21-23.
[3] 唐霖露,谈毅.中国风险投资机构联合投资绩效研究——来自中国IPO市场的实证研究[J].复旦学报(自然科学版),2015,54(3):336-342.

