晶界内耗研究的进展

孔庆平*，方前锋，蒋卫斌，崔平

中国科学院固体物理研究所材料物理实验室，合肥230031

晶界内耗研究的进展

孔庆平*，方前锋，蒋卫斌，崔平

中国科学院固体物理研究所材料物理实验室，合肥230031

固体在机械振动过程中由于材料内部原因引起的能量损耗称为内耗。晶界内耗峰是我国科学家葛庭燧于1947年用他发明的“葛氏扭摆”在多晶纯铝中发现的。晶界内耗峰和相关的滞弹性效应可以用滞弹性理论和粘滞性滑动模型给予合理的解释。这个内耗峰已被广泛地用来研究晶界的动力学行为，杂质在晶界的偏聚，以及材料科学中相关的问题。

以往晶界内耗的研究大多数是用多晶试样进行的，其中包含了不同类型晶界的贡献。由于不同类型晶界的结构和性质不同，因而多晶试样中的晶界内耗只能反映不同晶界的“平均效应”，它的具体机制也难以解释清楚。

二十一世纪以来，人们对双晶试样（其中只包含单一晶界）中的晶界内耗进行了比较细致的研究。实验结果表明，晶界内耗可以反映不同类型晶界的“个性”，因而可以应用于“晶界的设计和控制”（或称“晶界工程”）。此外，新近还发现了晶界内耗中的“耦合效应”和“补偿效应”。这些发现加深了对晶界内耗机制的认识。

本文首先对以往多晶试样中的晶界内耗研究做一个简要的概述，然后介绍近年来双晶试样中晶界内耗研究的新进展，并对晶界内耗的微观机制和应用前景进行分析和展望。

内耗；晶界；双晶；竹节晶；多晶；耦合效应；补偿效应

I.引言

固体在机械振动过程中由于材料内部原因引起的能量损耗称为内耗（Internal friction）。内耗（Q-1）的基本表达式是［1-6］

式中ΔW是在一个振动周期内单位体积的能量损耗，W是单位体积的最大弹性储能。比值ΔW/W是振动一周内的相对能量损耗，在工程上称为阻尼本领（Dam ping capacity），也可称消振本领。式中分母的2π因子表示：内耗是在一个单位弧度角内的相对能量损耗。

内耗研究有两方面的意义。第一方面，由于内耗越大则阻尼本领越大，内耗可以作为材料阻尼性能的指标。因而在选择和发展阻尼材料时，需要进行内耗的测量和改善阻尼性能的研究。高阻尼材料近年来受到许多国家的特别重视，从而发展出了一些性能优越的高阻尼材料。第二方面，由于内耗可以灵敏地反映材料内部结构单元的状态和运动变化，因而它已经发展成为研究材料内部结构单元（如点缺陷、位错、晶界、相界等）和结构转变的一种有力工具，在材料科学中得到了广泛的应用。通常测量内耗的交变应力是在弹性范围内，在应力撤除以后不发生残留应变，因而内耗是一种无损的检测工具。本文内容属于第二方面的研究。

晶界（grain boundary）是两个相邻晶粒（或晶体）之间的界面［7，8］。按照晶界两侧晶体点阵取向差的大小，通常把取向差小于15◦的称为小角度晶界，大于15◦的称为大角度晶界。小角度晶界的结构可以用分立的位错阵列来描述，并已得到实验观察的证实［9］。但是大角度晶界的结构还不够清楚。

近年来大角度晶界的重位点阵（Coincidence Site Lattice，CSL）模型，受到了广泛的认可［10-17］。根据重位点阵模型，当相邻晶粒的取向差为某些特定的角度时，两个晶粒互相重合的阵点在晶界上形成了重位点阵。这样的晶界称为“重位点阵晶界”（CSL晶界），或称“特殊晶界”。而那些偏离CSL取向差超过一定限度（Δθ=15◦∑-1/2）的晶界［12］，称为“无规晶界”，或称“一般晶界”。为了表示晶界上重合阵点的比例，人们引入了∑符号，用1/∑表示晶界上的重合阵点数在总阵点数中所占比例。∑的数值越低，则重合位置的比例越大。

已经发现低Σ（Σ≤29）的CSL晶界表现出一些特殊的性质［10-19］。例如，低Σ-CSL晶界的自由能一般低于无规晶界，即在一些CSL取向差处出现能量低谷。又如，高温形变和应力腐蚀的断裂通常发生在无规晶界处、而不在特殊晶界处。由于不同类型晶界对材料性能有不同的影响，因而人们希望在多晶材料中增加“有利的”晶界，而减少“有害的”晶界。这样的概念称为“晶界设计和控制”或称“晶界工程”［18，19］。

晶界内耗峰是葛庭燧在1947年在多晶纯铝中发现的［20，21］。这样的内耗峰后来又在多种金属和合金中发现［1-6］。它已被用来有效地研究晶界的动力学行为、杂质在晶界的偏聚、以及在形变和相变过程中晶界的变化等。葛庭燧曾对2000年以前晶界内耗的研究结果进行过总结和评述［4，22］。以往晶界内耗的研究大多数是用多晶试样进行的，其中包含着不同类型晶界的贡献。由于不同类型晶界的性质和结构不同，这样的晶界内耗只能反映不同晶界的“平均效应”，其具体机制也难以解释清楚。

21世纪以来，人们对双晶试样（其中只包含单一晶界）中的晶界内耗进行了比较细致的研究。实验结果表明，晶界内耗可以反映不同类型晶界的“个性”，因而可以应用于“晶界工程”。此外，新近还发现了晶界内耗中的“耦合效应”和“补偿效应”。这些发现加深了对晶界内耗机制的认识。

本文首先对以往多晶试样中的晶界内耗研究做一个简要的概述，然后介绍近年来双晶试样中晶界内耗研究的新进展，并对晶界内耗的微观机制和应用前景进行分析和展望。

II.多晶试样中的晶界内耗研究

A.晶界内耗峰和相关的滞弹性效应

葛庭燧于1947年用他发明的“葛氏扭摆”，首次在多晶Al试样中发现了晶界内耗峰，如图1（a）所示［20］，测量频率在室温时为0.8 Hz。由图可见，在285◦C附近出现了一个显著的内耗峰。而作为对比的单晶试样，内耗是随着温度单调上升的。因此，多晶试样中出现的内耗峰是由晶界引起的。在测量内耗的同时，葛庭燧还测量了纯A l多晶和单晶试样的切变模量（正比于f2，f是测量频率）随温度的变化，如图1（b）所示［20］。由图可见，在200◦C以下多晶和单晶Al试样的模量曲线基本上都是直线。多晶试样的切变模量在200◦C左右开始急剧降低，而单晶试样的模量并没有发生这种变化。

除了晶界内耗和切变模量以外，葛庭燧还用他研制的“扭转线圈装置”研究了多晶纯Al的另外两种滞弹性效应：恒应力下的微蠕变，和恒应变下的应力弛豫［20］。

Zener曾根据Boltzmann线性叠加原理，推导出四种滞弹性效应（内耗，切变模量，微蠕变和应力弛豫）之间的关系式［1］。葛庭燧用这些关系式把多晶纯铝的蠕变、动态切变模量以及内耗数据，都换算成在200◦C的应力弛豫数据，结果由每种数据换算出来的结果都与应力弛豫的实验值密切相合［20，21］，从而证明了滞弹性基本方程的有效性。

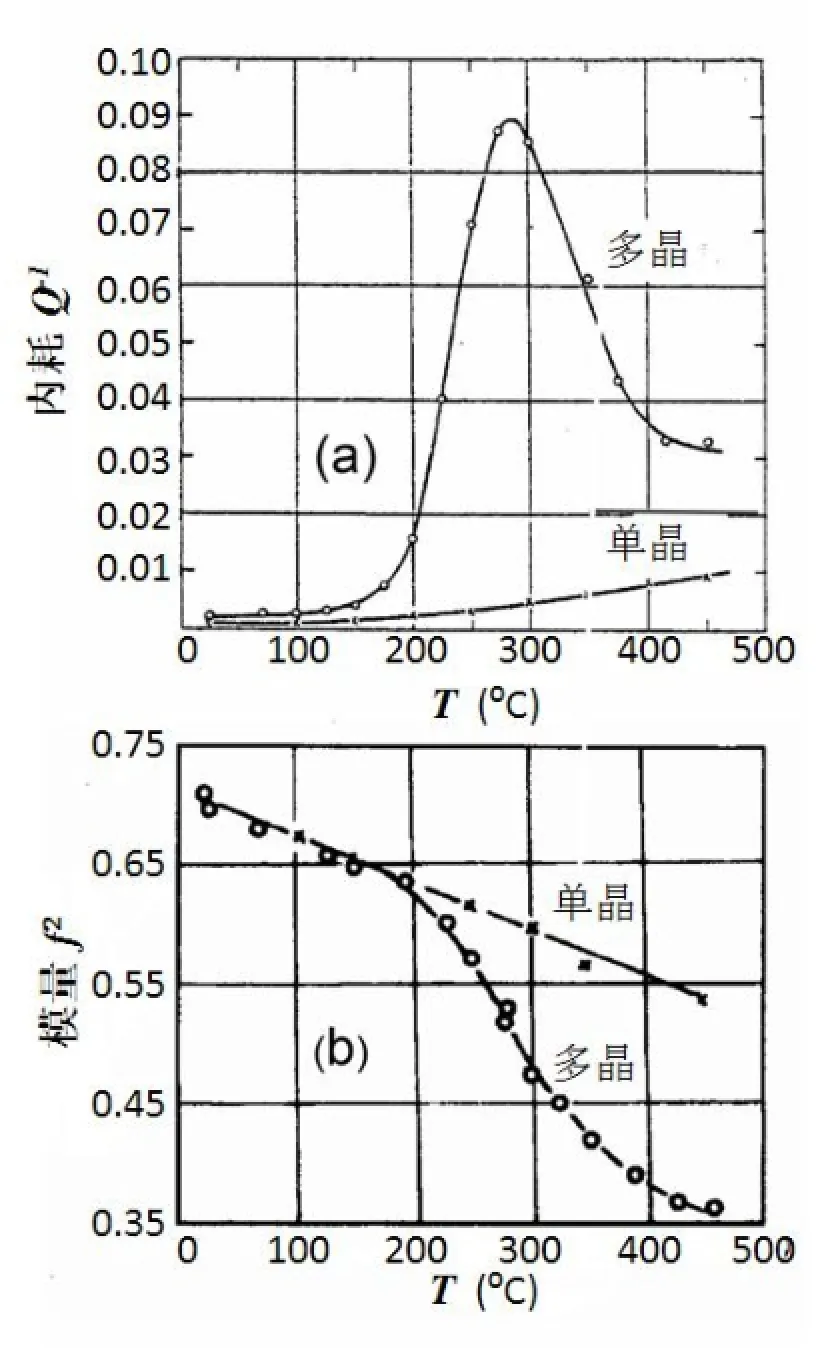
图1.纯铝多晶和单晶试样中（a）内耗、和（b）切变模量（f2）随温度的变化［20］

葛庭燧的上述研究结果于1947年发表，Zener教授随即于1948年出版了他的经典名著“金属的弹性和滞弹性”［1］，书中详细引证了葛庭燧的实验结果，作为滞弹性内耗理论的实验证据。由于葛庭燧对内耗和滞弹性领域作出了奠基性的贡献，因而他被国际上公认为内耗和滞弹性领域的奠基人之一。

B.滞弹性理论和晶界粘滞性滑动模型

晶界内耗和相关的滞弹性效应可以用Zener的滞弹性理论（Anelastic theory）和晶界粘滞性滑动模型（Viscous slid ing m odel）［1］给予合理的解释。

内耗的产生是与材料的滞弹性（Anelasticity）相联系的。材料在受到弹性应力后，应变一般要经过一个弛豫过程才能达到与应力相应的平衡值。在应力撤除后，应变又经过弛豫过程逐渐回复到零。由于应变落后于应力（滞弹性），才产生了振动能量的损耗。如果材料是理想的弹性体，应变与应力同步，是不会产生内耗的。如果应力采用正弦波的形式，

式中σ0是应力振幅，ω是角频率（ω=2πf，f是测量频率），t是时间，则应变可表示为

式中ε0是应变振幅，ϕ是应变落后于应力的相角差。利用（2）式和（3）式，可以求出一个振动周期内的损耗能量ΔW和最大弹性储能W分别为

由（4）式和（5）式就可以得到

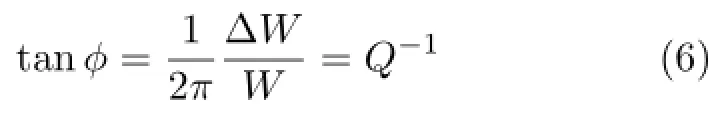
可见tanϕ（或者小内耗情况下近似为ϕ）也可以作为内耗的一种量度。

C.Zener教授提出了一个三参量模型，用来描述滞弹性固体的力学行为，如图2所示［1］。图中（a）弹簧JU和（b）弹簧δJ表示固体的弹性，（c）阻尼器η表示固体的粘滞性。图中（b）和（c）组成了一个并联单元，再与（a）串联起来。由图可见，当t=0施加应力时，并联单元和弹簧（a）同时承受了这一应力。弹簧（a）立即产生形变。由于阻尼器的存在，并联单元不能立即产生形变。随着时间的推移，阻尼器（c）开始运动，但阻尼器（c）的粘滞性运动受弹簧（b）的约束。

由三参量模型推导出的滞弹性固体的应力-应变方程为［1］

式中σ是应力，ε是应变，t是时间，a1，a2，b1，b2是材料常数。

将应力和应变的表达式（2）、（3）或它们的复数形式代入（7）式，可得出

图2.标准滞弹性固体的三参量模型［1］

式中τ是弛豫时间，Δ是弛豫强度（Relaxation strength），其定义为

其中MU和MR分别表示未弛豫和弛豫的弹性模量（Modu lus），JU和JR分别表示未弛豫和弛豫的弹性顺度（Com pliance），δM=（MU-MR）是弹性模量的弛豫量，δJ=（JR-JU）是弹性顺度的弛豫量。

由（8）式可见，当ωτ=1时，内耗会出现一个峰值。如果弛豫过程的速率受某种热激活过程控制，则弛豫时间τ将随着温度T的变化而变化，通常遵从以下的A rrhenius关系

式中τ0是指数前因子，H是激活能，k是Boltzmann常数。当

时，会出现一个内耗峰，Tp是内耗峰的最大值对应的温度（峰温）。因此，在一定的频率下测量就会出现一个随温度变化的内耗峰，或者在一定的温度下测量就会出现一个随频率变化的内耗峰。由内耗峰出现的温度与测量频率的关系，就可以按（11）式求出弛豫过程的激活能H和弛豫时间指数前因子τ0，它们是表征内耗源动力学性质的重要参量。

晶界粘滞性滑动模型，实际上就是把滞弹性固体的力学模型（图2）应用到晶界弛豫的情况。在切应力的作用下，晶界发生了粘滞性滑动（阻尼器（c）起作用），因而引起了能量损耗。假定多晶材料中的晶界角限制了晶界滑动的距离（弹簧（b）起作用），就使得内耗峰能够出现。

根据晶界粘滞性滑动模型，晶界的力学行为服从粘滞性流动的规律，即滑动速率与应力成正比、而与粘滞系数（η）成反比，但这并不意味着晶界的结构都是无序的。事实上，晶界的结构可以看成：既包含无序区，也包含有序区［23，24］。

为了解释晶界内耗的微观过程，Mott于1948年提出了“小岛模型”［23］，见图3（a）。葛庭燧于1949年提出了“无序原子群模型”［24］，见图3（b）。

图3.（a）M ott的小岛模型［23］，（b）葛庭燧的无序原子群模型［24］

Mott的“小岛模型”认为，晶界中包含着许多原子排列整齐的“小岛”，而这些小岛散布在原子排列较为混乱的区域中。他认为晶界滑动的元过程是小岛边缘的一些原子的熔化或无序化。葛庭燧的“无序原子群模型”认为，晶界中包含着众多的无序原子群，而它们的周围是原子匹配较好的点阵区域。在热激活和外加应力的作用下，无序原子群中的原子重排将引起晶界的局域滑动，并累积成为晶界的整体滑动。

根据这两个模型，Mott和葛庭燧分别推导出的晶界滑动速率表达式如下

式中A是一个常数。上式表明晶界滑动速率与应力成正比，与晶界滑动的粘滞性相符。上述这两个模型是最早解释晶界内耗微观过程的模型，也是最早的大角度晶界的结构模型。这表明晶界内耗的研究可以与晶界微观结构的研究联系起来。后来一些学者提出了其它的微观模型，本文将在第IV节中加以分析和讨论。

C.多晶试样中晶界内耗峰的特征

除了纯Al以外，葛庭燧还首先观察到了Cu、Fe、M g金属和Cu-Zn合金中的晶界内耗峰［25］。后来国内外的许多科学工作者又陆续在多种金属和合金的多晶材料中观察到了晶界内耗峰，并进行了细致的研究。其中代表性的工作有：Al［20-22，25-30］，Ag［29，31，32］，Au［29，33-35］，Cu［29，30，34，36］，Ni［29，37］，Fe［38，39］，Mo［40］，W［41，42］，Ti［43-45］，Zr［46-48］，Mg［49-52］，Zn［53，54］，Cu-Zn［55］，Ni-Cr［56，57］，Au-Ag-Cu［58，59］等。这说明晶界内耗峰是一个普遍的现象。在一定的频率下测量内耗随温度的变化时，只要温区内不发生结构转变，晶界内耗峰在升温或降温过程中都能够重复出现。当测量频率在1 Hz附近时，内耗峰出现的温度一般在0.4～0.7 T m之间（T m是熔点绝对温度），这取决于试样的纯度、制备工艺和热处理。

晶界内耗峰的一个特征是：它是由晶界引起的，在不含晶界的单晶试样中不出现。这已由许多金属（如A l［20］，Au［49］，Mg［52］）的多晶与单晶试样的对比实验所证实。在1970-1980年代，国外曾有人［60-63］在经过轻度冷加工的纯铝单晶中观察到一个较低的“内耗峰”，与纯铝多晶中的内耗峰温接近。因而他们怀疑多晶中的内耗峰可能是由位错引起，而不是由晶界引起。为了澄清这些怀疑，葛庭燧、崔平和苏全民［26］采用三种不同方法制备出了纯A l单晶试样，与多晶试样进行对比实验。结果再次表明，多晶试样中的“葛峰”在这三种单晶试样中均不出现，从而澄清了这些怀疑［64，65］。至于经过冷加工的单晶试样在“葛峰”温度附近出现的不稳定的“内耗峰”，可能与冷加工和部分回复形成的某种位错亚结构有关。只有在再结晶温度以上充分退火后形成了稳定的晶粒和清晰的晶界，才能得到真正的晶界内耗峰。

晶界内耗峰另一个特征是，它是由晶界的滞弹性弛豫引起的。其行为符合上节所述滞弹性理论的预期，即晶界内耗峰不但出现在一定频率下的“内耗-温度谱”中，而且也出现在一定温度下的“内耗-频率谱”中。

袁立曦和葛庭燧用99.999%多晶纯铝在“内耗-温度谱”和“内耗-频率谱”中观测到的晶界内耗峰，如图4（a，b）所示［66］。图4（a）曲线a～e分别表示在频率0.4，0.17，0.095，0.053和0.017 Hz下测出的内耗-温度谱，由图可见，内耗峰随着测量频率的增高向高温移动。图4（b）曲线a～e分别表示在温度214， 204，195，186和176◦C下测出的内耗-频率谱。由图可见，内耗峰随着测量温度的增高向高频移动。根据（11）式，由这两种测量中内耗峰的移动得出的弛豫参量（H=1.5 eV，τ0=4×10-17s）是一致的。这就证明了：这两种方法测出的是同一个晶界内耗峰，并且它是由滞弹性弛豫引起的。

图4.多晶纯铝中的（a）内耗-温度谱，和（b）内耗-频率谱［66］

应该指出，虽然多晶试样中晶界内耗峰的观察和研究已积累了大量的资料，但是晶界内耗峰的激活参量（H和τ0等）的物理意义还没有得到满意的解释［2，4］。

由于不同作者所用试样的纯度不同，即使标称纯度相同、其中杂质的种类也可能不同，加上试样制备和实验条件的不同，因而不同作者对同一种材料测出的表观激活能H值会出现差别。它很难与晶界扩散激活能Hgb或自扩散激活能Hsd值对应起来。有些纯金属的H与Hgb相近，而有些纯金属的H则与Hsd相近，甚至有时还高于Hsd。因此，H的物理意义不能简单地从单原子过程来理解，可能需要考虑多原子的群体过程以及杂质影响等因素。

关于晶界内耗的弛豫时间指数前因子τ0，实验观测到的值有些在13～15附近，接近于单原子过程的数量级；有些高于这个范围，也暗示着一种多原子的群体过程。

另外，几乎所有观测到的多晶试样中晶界内耗峰的宽度都大于单一弛豫时间的情况。Now ick和Berry认为内耗峰的展宽是由于弛豫时间的分布引起的，并引入参数β作为弛豫时间τ的分布函数，它由两部分组成［2］

式中β0表示τ0的分布，βH表示H的分布，其中βH在τ的分布中起较重要的作用。β值愈大则内耗峰愈宽。在单一弛豫时间的情况下β=0，半高宽为Δ（logωτ）=1.144。一些多晶试样（如A l，Cu等）晶界内耗峰的β值在3～4附近，其半高宽约为单一弛豫时间的2～3倍。

多晶试样晶界内耗的表观激活能H和弛豫时间指数前因子τ0的物理意义，以及内耗峰展宽的原因，是长期以来没有得到满意解决的问题。本文第III.C.节将根据新近的研究结果，从“耦合作用”（多原子的耦合运动）的角度加以分析。

D.竹节晶试样中的晶界内耗峰

在通常的多晶试样中，晶界的排列是无序的，而在竹节晶试样中，晶界是近似平行排列的，并且每个晶界的面积都与试样的横截面相等。葛庭燧等用冷加工然后高温退火的方法，制备了纯铝竹节晶试样（试样长度10 cm，直径1mm），并对其中的晶界内耗峰进行了详细的研究［67-70］。

图5（a）表示99.999%纯A l的竹节晶试样中的晶界内耗峰，试样中含有的竹节晶界数目N=30，测量频率是1.5 Hz。他们发现，竹节晶界内耗峰的高度与试样中竹节晶界的数目N成正比，如图5（b）所示［67］。由于每个晶界的面积都与试样的横截面相等，因而上述实验结果表明，晶界内耗峰的高度是与试样中晶界的总面积成正比的。图中的直线通过原点，表明没有晶界就不出现这个内耗峰。这也证明了所观察到的内耗峰是由晶界引起的。

他们又对99.9999%高纯A l试样中的晶界内耗峰进行了研究，发现晶界内耗峰高度也与竹节晶界的数目N成正比［68］。

以往在解释多晶试样中出现晶界内耗峰时，曾假定试样中的晶界角是限制晶界滑动距离的因素［1］。既然在竹节晶试样中不存在晶界角，因而晶界角并不是限制晶界滑动的必要因素。为了考查试样的氧化铝表面层是否限制了晶界滑动，他们将竹节晶纯Al试样的Al2O3表面层用氩离子减薄技术剥除，用俄歇技术肯定了试样的A l基体已完全暴露出来，再在高真空中测量内耗。结果表明，剥除A l2O3表面层前后的竹节晶界内耗峰没有差别。这就表明试样的表面层并不是限制晶界滑动的重要因素［69］。他们通过对竹节晶试样的透射电子显微镜观察（TEM）指出，晶内位错与晶界的交互作用可能是限制晶界滑动的因素［70］。

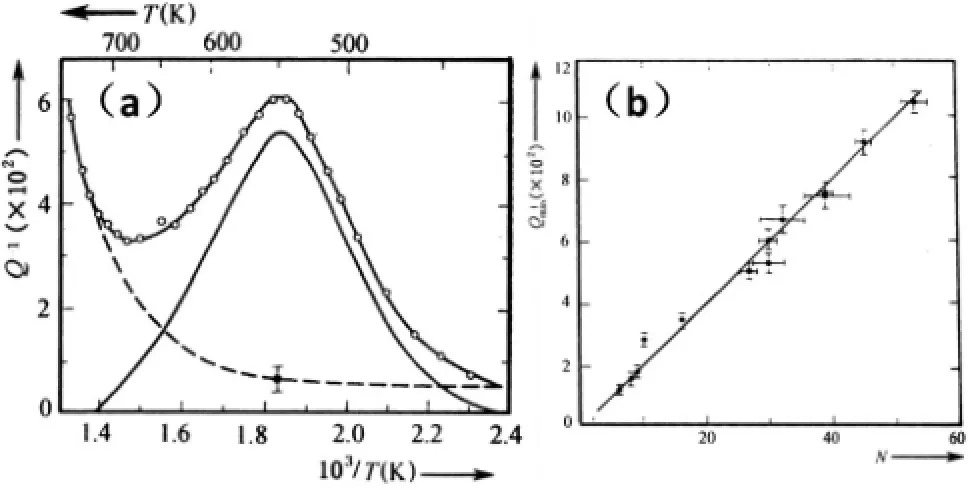
图5.纯铝中的（a）竹节晶界内耗峰（N=30），（b）内耗峰高度与竹节晶界数目成正比［67］

E.晶界内耗在材料科学中的一些应用

1.杂质偏聚对晶界内耗峰的影响

杂质一般倾向于偏析到基体的晶界上以降低自由能［71］。由于杂质对晶界内耗峰的弛豫强度和弛豫参量有显著的影响，因而晶界内耗峰已被有效地用来研究杂质在晶界的偏聚及其对材料性能的影响［36，39，72-77］。

由于杂质含量和存在状态的不同，同一种基体材料的晶界内耗峰可以有三种不同的状态：（a）纯净晶界峰（简称PM峰），即在试样纯度很高、其中杂质的影响可以忽略时观察到的晶界峰；（b）固溶晶界峰（简称SS峰），即所含杂质在固溶状态时观察到的晶界峰；（c）沉淀晶界峰，即在晶界含有沉淀或第二相颗粒时观察到的晶界峰［2，4］。

在一定频率下测量内耗时，固溶晶界峰的峰温一般高于纯净晶界峰，这可归因于试样中所含的固溶杂质使激活能增大和弛豫时间增长。沉淀晶界峰的峰温和峰高一般比固溶晶界峰较低，这可归因于沉淀颗粒增多使弛豫时间缩短和弛豫强度降低。

实际上，纯净晶界峰和固溶晶界峰只是在杂质含量上有相对的差别，二者并没有一个明确的界限。在只观察到一个晶界内耗峰的情况下，就难以辨别它是纯净峰、固溶峰、或者二者的叠加。在适当的条件下，可以同时观察到这两个分立的内耗峰，并且当固溶杂质浓度逐渐增加时，纯净峰和固溶峰是相互消长的。

例如，W ienig和Machlin研究了99.999%纯Cu中掺入不同A l含量（0.03at%-0.8at%Al）对晶界内耗峰的影响，观察到了纯净峰和固溶峰相互消长的关系，如图6所示。纯Cu的晶界峰的温度较低，在Cu-0.03%A l试样中出现了两个内耗峰：即纯净峰和固溶峰。随着A l含量的增加，纯净峰消失，而固溶峰的高度增高、峰温也升高［36］。

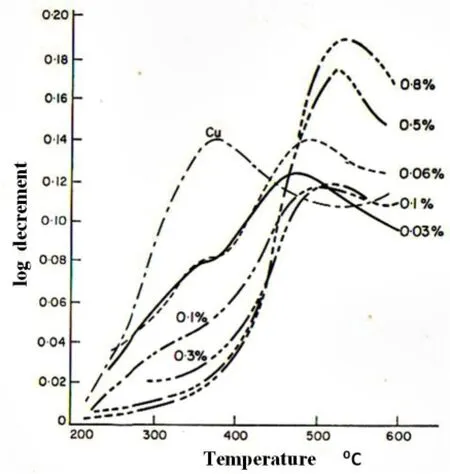
图6.99.999%纯Cu中掺入不同A l含量对晶界内耗峰的影响［36］

王业宁和朱劲松［74］研究了微量C对αFe中晶界内耗峰的影响。观察到当αFe中的C含量完全去除时，只出现一个纯净晶界峰，而在Fe中掺0.00051%C后，纯净晶界峰和固溶晶界峰可以同时出现。

葛庭燧和崔平［75］研究了杂质含量不同的Al多晶试样的晶界内耗，观察到上述三种不同的晶界内耗峰。他们称99.9999%纯A l中的晶界内耗峰是“纯净晶界峰”，当纯A l中的少量杂质以固溶状态存在时，其晶界内耗峰是“固溶晶界峰”。而A l-1.2 w t%Cu的晶界中有沉淀相出现，因而其晶界内耗峰是沉淀晶界峰。

Mori等研究了Cu-0.006w t%Si多晶试样由于内部氧化而产生的球状SiO2颗粒对于Cu晶界弛豫的影响［76］。他们在465 K（0.3 Hz）观察到一个“沉淀晶界峰”，峰温低于纯Cu的晶界峰。

戢景文等研究了稀土元素La（0.58-0.72w t%）对Fe-P合金中晶界内耗峰的影响。发现La的加入使Fe-P合金中晶界内耗峰的峰高降低，峰温升高。说明La的加入起了稳定晶界的作用［39］。

2.形变对晶界内耗峰的影响

多晶试样在冷加工形变后，会引起晶界严重畸变，使晶界滑动受到抑制，因而晶界内耗峰被抑制，或者被冷加工引起的高背景内耗所掩盖。随着退火温度的升高，晶界内耗峰将逐渐回复。只有在再结晶温度以上充分退火，生成新的晶粒和清晰的晶界后，才能观察到完整的晶界内耗峰。因而晶界内耗峰已被用来研究形变、回复和再结晶的过程［78，79］。

另一方面，多晶材料在适当的温度和应力下形变后，原来的晶界依然存在。但晶界内耗峰的弛豫参量和弛豫强度发生了不同程度的变化。因而可以通过晶界内耗峰的测量，研究晶界在形变过程中发生的变化［80-84］。

孔庆平和戴勇研究了纯Cu多晶试样在导致不同断裂类型的形变过程中晶界内耗峰的变化［78-80］。他们在较高应力和较低温度（导致穿晶型断裂）的形变过程中，发现晶界内耗峰的高度降低、激活能增高，说明晶界强度在形变中增高；而在较高温度和较低应力（导致沿晶型断裂）的形变过程中，晶界内耗峰的高度和激活能变化不大，说明晶界强度在形变中变化不大。电镜观察显示，穿晶断裂过程中晶界发生强化是由于晶界发生了扭曲、以及位错与晶界的交互作用所引起。而在沿晶断裂的形变过程中晶界较为平直、位错与晶界的交截比较少见，因而晶界强度变化不大。上述晶界内耗的工作表明，形变断裂类型不仅是由外部的实验条件决定，而且与试样内部的晶界状态和强度在形变中的不同变化有关。

3.薄膜和超细晶材料中的晶界内耗

以上几节叙述的是常规多晶材料中的晶界内耗。最近几十年来，人们对一些非常规的多晶材料（如薄膜材料）的晶界内耗，进行了大量的研究［85-89］。例如，Bohn及其合作者研究过纯Al薄膜材料（厚度为µm量级）中的晶界内耗峰［86-88］。他们观察到纯A l薄膜中晶界内耗的激活能约为H=0.6 eV，而同样成分纯A l块材的晶界内耗激活能约为H=1.4 eV。他们由此认为：晶界内耗在薄膜材料中的速率控制过程可能是晶界扩散，而在块材中的速率控制过程可能是体扩散。

超细晶（纳米晶和亚微米晶）材料的晶界内耗也已有大量研究。在一些纯金属（如Pb，A l，Cu，Ag，Fe等）纳米晶材料中，观察到了一个或两个晶界内耗峰［90-96］。这些内耗峰的弛豫参量由于制备方法和退火温度的不同而有一些差别。

另外，用“等通道转角挤压法”（Equal-channel angu lar p ressing，ECAP）制备超细晶材料的工作已大量开展，也观察到了这些超细晶材料中的晶界内耗峰，例如文献［97-100］。但这些超细晶材料中的晶界内耗峰往往是不够稳定的。可能由于残留应力的影响，它们的弛豫参量难以准确测定。而用升温退火的方法消除残留应力，又会使晶粒长大。超细晶材料中的晶界内耗研究可以提供晶界的稳定性及其对性能影响的有用知识，有待进一步开拓。

III.双晶试样中的晶界内耗研究

上面几节所述是多晶试样（包括竹节晶试样）的晶界内耗。由于多晶试样的晶界内耗是试样中各种晶界的内耗的综合贡献，它所反映的是不同晶界的“平均效应”。多年来国内外的研究表明，不同类型的晶界有着不同的结构、以及不同的力学、物理和化学性质［10］。为了研究不同类型晶界的“个性”，有必要研究双晶试样（其中只含单一晶界）的晶界内耗。以往Iwasaki［28］和葛庭燧等［101］曾经在纯A l双晶试样中观察到晶界内耗峰，但没有进行不同类型和不同取向差的晶界内耗研究［4］。

二十一世纪以来，中科院固体物理所在葛庭燧先生以往工作的基础上，与德国亚琛大学合作制备了三十多种不同类型不同取向差的99.999%纯Al双晶试样。其中含有以＜112＞、＜100＞和＜111＞为转轴的倾侧晶界、以及以＜111＞为转轴的扭转晶界。对这些双晶试样中的晶界内耗，进行了比较细致的研究，取得了一些新的进展。发现在不同类型的双晶试样中，晶界内耗的弛豫参量有明显差别，反映了不同类型晶界的结构特征，并发现了晶界内耗中的“耦合效应”和“补偿效应”，加深了对晶界内耗微观机制的认识，并启示了晶界内耗新的应用前景［102-110］。

内耗测量的设备是合肥固体物理所研制的“自动化扭摆”（又称“多功能内耗仪”）。它可以在一次升温或降温过程中测量出几个频率的内耗和模量的变化，所用的测量频率在0.1-10 Hz范围。采用强迫振动模式，应变振幅为≤10-5。用自己编制的计算机软件求出H，τ0，Δ等弛豫参量。

A.双晶试样中的晶界内耗峰

图7（a，b）分别表示一种小角度倾侧晶界和一种大角度无规倾侧晶界的内耗峰（f=1 Hz）［106］。此内耗峰在单晶（由双晶旁切出）中不出现，作为对比的单晶和双晶试样的成分和历史完全相同。这表明这个内耗峰是由双晶中的晶界引起的。图8（a，b）分别表示双晶中的晶界内耗峰和模量曲线均随频率的增高向高温移动［106］。

图7.双晶试样中的晶界内耗峰：（a）＜100＞7.5°（b）＜112＞40.2°［106］

图8.不同频率测量的（a）内耗峰，（b）动态模量曲线［106］

为了进一步证明双晶中的内耗峰是由晶界引起的，研究了晶界密度（试样单位体积中的晶界面积）对内耗峰高度和弛豫强度的影响。常用的双晶试样长度为50 mm，横截面为4×2 mm2（试样1）。为了改变晶界密度，将试样宽度两侧各截去1 mm，使试样横截面变成2×2 mm2（试样2）。而试样长度和居中的晶界面积50×2mm2保持不变，如图9所示［109］。这样，试样2的体积是试样1的一半，晶界密度则是试样1的二倍。

图9.双晶（a）试样1和（b）试样2［109］

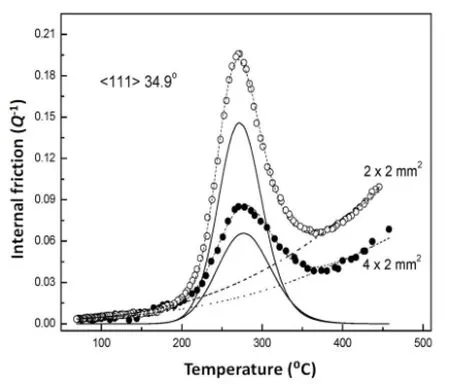
图10.晶界密度对内耗峰高度的影响［109］

图10表示晶界密度不同的两种试样晶界内耗峰的比较［109］。由图可见，在相同频率下（1 Hz）晶界内耗峰的峰温不变，试样2的内耗峰高度是试样1的二倍（图中实线是扣除背景后的内耗峰），即内耗峰高度正比于晶界密度。

图11表示两种试样内耗峰的温度随频率改变发生了相同程度的移动［109］，由此求出的激活能H和弛豫时间指数前因子τ0相同，表明晶界密度的改变并不改变晶界弛豫的机制。

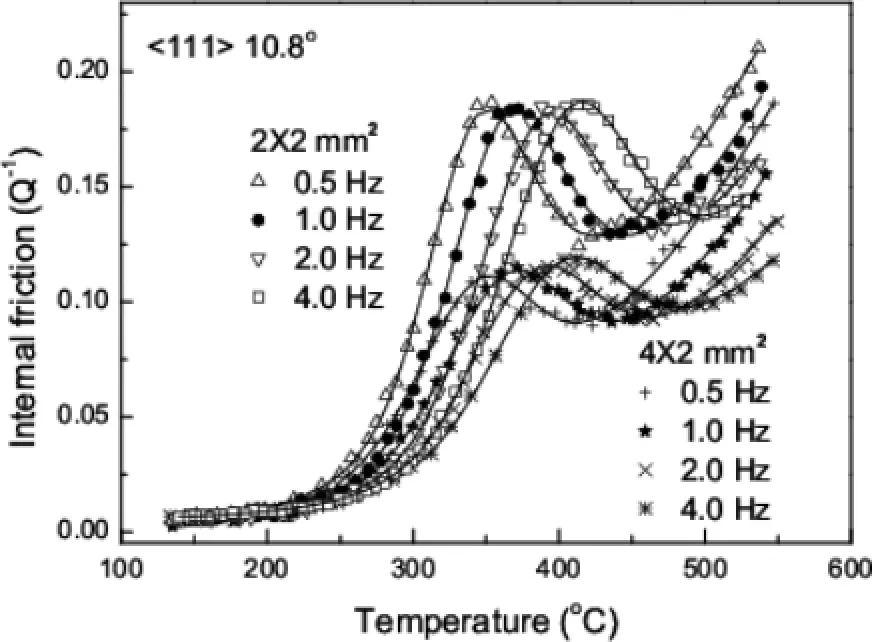
图11.晶界密度不同的两种试样晶界内耗峰随测量频率的移动［109］

不同晶界密度的实验结果可以从内耗的基本表达式（1）出发得到解释。

式中ΔW是单位体积振动一周内损耗的能量，W是单位体积最大弹性储能。假定试样的体积是V，则总的储能是W×V。如果这个内耗峰是由晶界弛豫引起的，则ΔW应该与试样中晶界的总面积A成正比。因而上式可改写为

式中ΔWb是单位晶界面积在一周内损耗的能量，在此实验条件下（1/2π）（ΔWb/W）是恒量，其量纲是（m3/m2）。由（14）式可见，内耗峰高度应该与晶界密度（A/V）成正比，与实验结果相符。这就进一步证明了双晶中的内耗峰是由双晶中的晶界引起的。

B.双晶试样在内耗测量时的晶界滑移

在内耗测量时，双晶试样（长度为50 mm）的下端固定，上端往复扭转。对双晶试样的应力分析表明，在内耗测量时晶界发生了滑动和扭转［109］。由于扭转消耗的应变能相对于滑动可以忽略［9］，因而内耗主要是由晶界滑动引起的。根据晶界滑动模型，可以由晶界弛豫强度的数据，估算出晶界滑动引起的应变εa在试样总应变ε中的比例、以及内耗测量时的晶界滑移量。

内耗测量时的应变振幅为ε=10-5，其中包括基体的弹性应变ε0和由晶界滑动引起的滞弹性应变εa。为了求出εa/ε，用下面的公式［1，2］

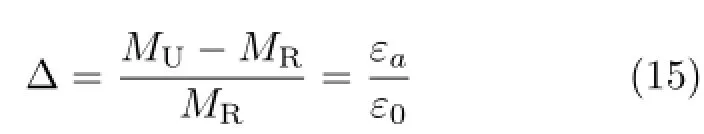
式中Δ是弛豫强度，MU和MR分别是未弛豫和弛豫的模量。根据（15）式可得

利用弛豫强度的实验数据，用（16）式得出试样1和2的εa/ε分别等于15～24%和24～38%［109］。

根据应变振幅（ε=10-5）和试样1，2的宽度（d1=4 mm；d2=2 mm），可以算出：试样1，2平行于晶界面的总位移分别为：x1=εd1=40 nm，x2=εd2=20 nm。因而，双晶试样1，2在内耗测量时的晶界滑移量分别是

这些数值与Ray和Ashby［111］对多晶纯铝（晶粒尺寸0.1 mm）的估算值（5 nm）数量级相同。

C.不同类型晶界的弛豫参量

在所研究的三十多种纯铝双晶中，都观察到了显著的晶界内耗峰（Σ3晶界除外，见本节后半部分）。双晶中的晶界内耗峰，像多晶中的晶界内耗峰一样，都随频率的增高向高温移动。由不同频率的测量，得出了它们的弛豫参量（H，τ0等）。图12表示几种以＜111＞为转轴的倾侧晶界和扭转晶界的A rrhenius图（lnω～1/Tp）［110］。由图中直线的斜率可以看出，小角度倾侧晶界的表观激活能比大角度倾侧晶界的明显较低；而在扭转晶界中，小角度与大角度晶界的表观激活能没有明显差别：并且扭转晶界的表观激活能都大于倾侧晶界的相应值。

图12.几种＜111＞双晶的A rrhenius图：（1）10.8°，（2）18.3°，（3）34.9°倾侧晶界；（4）10.9°，（5）36.0°扭转晶界［110］

实验数据表明，所研究的纯Al双晶中不同类型晶界的弛豫参量有以下四种情况［110］：

1.小角度倾侧晶界：它们的晶界弛豫激活能H为1.3～1.4 eV，弛豫速率指数前因子为1011～1013/s。

3.大角度低∑倾侧晶界（如∑5晶界）：H值在2.0 eV附近，值为1017～1018/s。

4.扭转晶界：＜111＞小角度和大角度扭转晶界的H值都在3.0 eV附近，τ0-1值为1024～1025/s。

但是，以＜111＞为转轴、取向差接近60◦（Σ3）的倾侧晶界和扭转晶界，晶界内耗峰不出现，内耗像单晶那样随温度单调上升（见图13）［110］。＜111＞60◦倾侧晶界是非共格的Σ3晶界，＜111＞60◦扭转晶界是共格的Σ3晶界。这就表明共格和非共格的Σ3晶界具有较高的抗变形能力。这个实验结果与Watanabe［19］观察到的Σ3晶界具有较强的抗高温断裂能力相符。

图13.取向差接近Σ3晶界的内耗：（a）59.0°倾侧晶界，（b）58.7°扭转晶界［110］

上述实验结果表明，不同类型晶界的弛豫参量有明显差别。弛豫参量的差别，是晶界结构不同的反映。因而可以用内耗方法来鉴别不同类型的晶界，并可应用于“晶界工程”。

D.晶界内耗中的耦合效应

考虑到晶界微观结构的复杂性和微量杂质的影响，在晶界弛豫过程中可能有耦合效应（Coup ling effect）发生，故采用一种耦合模型对内耗数据进行了分析。倪嘉陵（K.L.Ngai）等提出的耦合模型是建立在多体相互作用理论的基础上，已经成功地应用于许多关联体系的弛豫研究。这种耦合模型的基本思想是：在发生耦合作用的弛豫过程中存在一个临界时间tc，弛豫函数C（t）在tc前后的表达式分别是［112-116］：

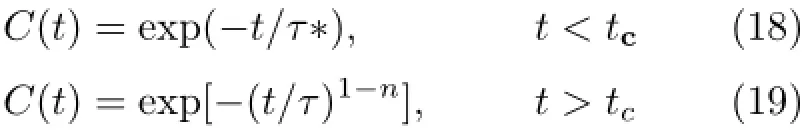
式中τ∗表示无耦合的弛豫时间，τ表示耦合的弛豫时间，n为耦合参数（0≤n＜1），它随着耦合强度的增大而增大。当t＜tc时，各弛豫元相互独立，服从简单的指数函数（18）式。而当t＞tc时，弛豫元之间发生交互作用，使弛豫速率降低，服从展宽的指数函数（19）式。

由于所用的内耗测量在低频范围（～1 Hz），tc（～10-12s）在弛豫过程中只占很小的比例［112］。因此，整个弛豫过程可以近似用（19）式描述。根据弛豫函数（18）和（19）在t=tc时的连续性，并考虑到弛豫时间与温度的A rrhenius关系，可以得到：

式中H∗和H分别表示解耦后的本征激活能和发生耦合时的表观激活能。τ∗o和τo分别表示解耦后和发生耦合时的弛豫时间指数前因子。

当n=0时，H∗=H。当n＞0时，表观激活能H和内耗峰宽度随着n的增大而增大，并且内耗峰形状变得不对称［112-116］。将（19）式经过傅立叶变换，内耗可以表示为温度（1/T）、频率（f）和耦合参数n的函数。用编制出的软件对内耗数据进行拟合，如图14所示，就可以求出耦合参数n［104］。

根据对内耗数据拟合的结果，得出了不同类型晶界内耗的耦合参数［110］。

2.大角度无规倾侧晶界：n=0.35～0.44。它们的晶界内耗机制可归因于晶界内无序原子群中的原子重新排列，涉及到原子的关联运动，因而表现出一定程度的耦合强度。

3.大角度低∑倾侧晶界：n≈0.5。这反映出低∑特殊晶界中原子排列比较紧密的结构特征。当晶界中的一个原子移动时，邻近的原子也要调整它们的位置使晶界保持在低能状态，其晶界内耗的机制可能涉及到较强的关联运动。

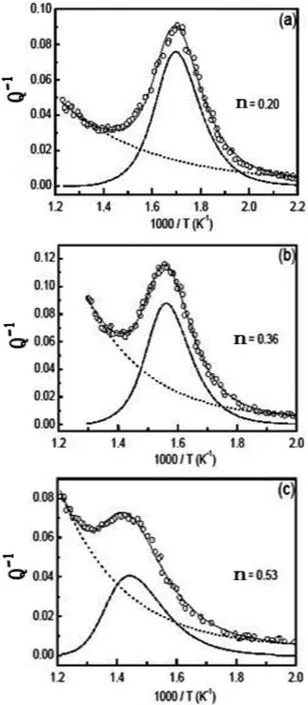
图14.几种倾侧晶界内耗数据的耦合分析：（a）＜100＞7.5°，（b）＜112＞40.2°，（c）＜100＞36.0°（∑5）［106］

4.扭转晶界（包括小角度和大角度晶界）：n≈0.68。这可能反映出扭转晶界中螺型位错网络的结构特征，网络中的结点强烈地滞缓了晶界滑动，因而发生了很强的耦合效应。

耦合强度的差别是不同类型晶界的结构特征的反映，从（20）式可以看出，耦合强度愈大则表观激活能H愈高。正是耦合强度的不同导致了表观激活能有不同程度的增高。将耦合参数n以及表观激活参量H和代入（20）式和（21）式，即可求出解耦后的本征激活能H∗和如图15所示。发现它们的本征激活能都处在（1.0±0.1 eV）水平，接近纯铝的晶界扩散激活能。这表明不同类型晶界内耗的基本机制是相同的，只是由于耦合强度不同才产生表观激活能的差异。

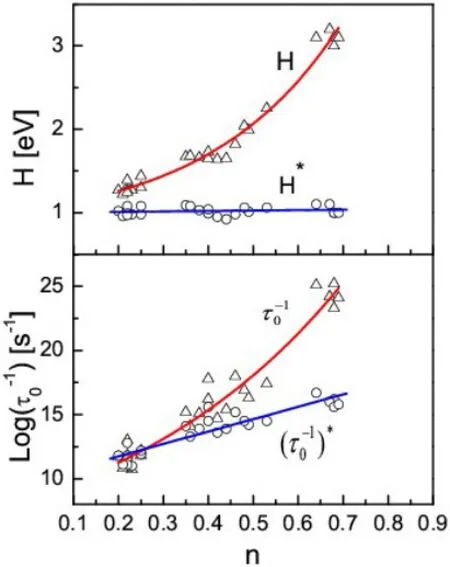
图15.表观弛豫参量（H和τ0-1）与耦合参数（n）之间的关系，H∗和τo-1∗表示解耦后的本征弛豫参量［110］

双晶试样的研究结果，不仅揭示了不同类型晶界的内耗不同特征，也有助于理解多晶试样晶界内耗的特点。由多晶试样测出的激活能等弛豫参量，实际上是试样中不同类型晶界的平均值（或最可几值）。当试样中晶界类型的比例（晶界特征分布）不同时，激活能等弛豫参量就可能发生变化。由于在通常的多晶试样中，大角度无规倾侧晶界占较大的比例，因而多晶试样晶界内耗的表观激活能通常与大角度无规倾侧晶界的相近。另外，多晶试样中晶界内耗峰的宽度，是各个晶界内耗峰宽度叠加的结果。晶界类型的分布将导致内耗峰进一步展宽，因而多晶试样中晶界内耗峰的宽度（β≈3.0～4.0）一般大于双晶的晶界内耗峰的宽度（β=1.2～2.5），正如实验观察到的那样。

E.晶界内耗中的补偿效应

我们还发现，双晶试样晶界内耗的表观激活能（H）与弛豫速率指数前因子的对数之间呈线性关系，如下式所示［107］

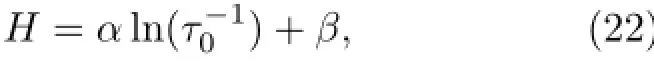
式中α和β是常数。图16表示这样的关系，由图可见，虽然不同类型晶界的H和值有很大的差别，但总体上符合（22）式。由弛豫速率的表达式

可见，H增大使弛豫速率τ-1减慢，增大使弛豫速率τ-1加速。H和的同步增减，对弛豫速率的快慢起到了补偿或调节作用，故（22）式称为“补偿效应”（Com pensation effect）。

图16.纯铝双晶试样晶界内耗中的补偿效应［107］

晶界内耗的基本过程可以归因于晶界区域内的原子扩散（单原子扩散或多原子扩散），因而其弛豫速率可以表示为

式中νD是原子振动频率，ΔS是激活熵，C是常数。比较（23）和（24）式可得

将（25）式代入（22）式可以得到

式中a和b是常数。（26）式表明表观激活能H与激活熵ΔS之间存在线性关系，二者是同步增减的。这就意味着：“耦合效应”不仅增高了表观激活能，而且同时增高了激活熵，二者的增高都是由于晶界中原子之间的“耦合效应”所引起的。耦合效应和补偿效应的发现和研究，加深了人们对晶界内耗微观机制的理解。

虽然晶界内耗中的”补偿效应”是在2009年初次观察到的［107］，但类似的补偿效应以前已经在晶界迁移和晶界滑动、以及晶界扩散中观察到［117-121］。它的物理本质尚待进一步研究。

IV.关于晶界内耗的机制

A.关于晶界粘滞性滑动模型

上述多晶、竹节晶和双晶的实验结果表明，晶界内耗峰和相关的滞弹性效应可以用滞弹性理论和晶界粘滞性滑动模型很好地加以解释。简单地说，内耗（能量消耗）是由晶界的粘滞性滑动引起的；而晶界的滑动由于受到某种结构单元的限制才出现了内耗峰。

图2的三参量模型可以很好地解释一个晶界内耗峰的出现。但有时也会观察到由晶界引起的两个内耗峰，如II.V.节中所述。在这样的情况下，就应该在三参量模型中增加一个或两个参量，用四参量或五参量模型来解释。

另外，根据目前已知的研究结果，经典的粘滞性滑动模型中的某些假定需要加以修改或补充。例如，在经典的粘滞性滑动模型中［1，122］，曾假定多晶试样中晶界的滑动受到了晶界角的限制才使内耗峰出现。但是，如第II、III节所述，在不含晶界角的竹节晶和双晶试样中也能够出现晶界内耗峰。这就说明，限制晶界滑动的结构单元不仅是晶界角，还有其它的结构单元。

许多实验结果表明，晶界通常是不平坦的，而是包含着许多起伏不平、尺寸均匀的小面，这些小面的取向稍微偏离整个晶界的“平均面”［10，123-125］。因此可以设想，这些“小面交界”（Facet junctions）有可能成为限制晶界滑动的结构单元。下面我们采用“小面交界”模型来估算内耗测量时双晶试样中晶界的滑动距离。

Ray和Ashby曾于1971年根据晶界粘滞性滑动模型，估算过在内耗测量时多晶试样中的晶界平均滑动距离［111］。他们假定多晶试样中的晶界面近似于正弦波的形状，推导出的公式是

式中U是晶界平均滑动距离，λ和h分别是晶界形状的波长和振幅，τa是切应力，E是杨氏模量，ν是泊松比。他们得出多晶试样中的晶界平均滑动距离约为5 nm。

根据文献上的观察结果［10，123-125］，假定双晶中晶界内小面的平均尺寸为λ≈500 nm，h≈2～3 nm，用（27）式估算出内耗测量时双晶试样中晶界滑动的平均距离约为6～13 nm［109］。这个结果与我们在III.B.节中用弛豫强度和试样尺寸数据估算的结果相符。因而我们认为，采用“小面交界”作为限制晶界滑动的结构单元是可行的。

“小面交界”可能以晶界中的台阶（高度为一个原子尺寸）的形式限制晶界的滑动，也可能以晶界中位错的形式存在。在后一种情况下，位错网络中位错段的线张力也可以限制晶界的滑动（参见IV.B.节）。

B.关于晶界内耗的微观机制

1.晶界内耗的一些微观模型

早在1948和1949年，Mott［23］和葛庭燧［24］就分别提出了“小岛模型”和“无序原子群模型”，用来解释晶界内耗的微观过程。他们分别推导出晶界滑动速率与外加应力成正比，解释了晶界在外力作用下表现出的粘滞性质。这两个模型都认为晶界内包含着有序区域和无序区域。晶界滑动的元过程在“小岛模型”中认为是小岛周围原子的“熔化”（即“无序化”）；而在“无序原子群模型”中认为是无序原子群内的原子重新排列。这两个模型对于解释大角度无规晶界的内耗仍然是合适的。

后来，位错模型逐渐引用到晶界内耗的机制中来。例如，Robelts和Barrand在1968年用层错能不同导致位错宽度不同的概念、解释了不同金属中弛豫强度的差别［37］。

Ashm arin，Zhikharev和Shvelov于1977年提出了“位错网络模型”（dislocation-networkm odel），用来解释晶界内耗的微观机制［126-128］。他们认为，晶界内耗是由于晶界位错的运动引起的，而两端被钉扎的位错的线张力是限制晶界滑动的因素。他们推导出的晶界内耗表达式是

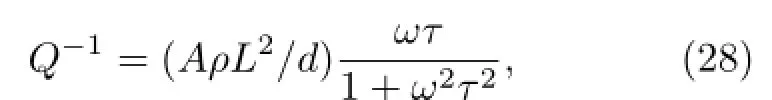
其弛豫强度为

式中A是一个系数（≈0.1），ρ是晶界位错密度，L是位错段长度，d是多晶试样中的晶粒尺寸。他们用适当的位错段长度估算出了几种金属的晶界内耗的弛豫强度，与实验值大致相符［126，127］。他们还用这个模型研究了杂质对晶界内耗的影响［128］。

此外，孙宗琦和葛庭燧还提出了“连续分布位错”（continuous-distribution dislocation）的概念来解释大角度晶界的滑动机制［129，130］。Darinskii等提出晶界滑动过程是由晶界位错和台阶等结构单元的重新组合完成的［131，132］。

上述的位错模型（特别是位错网络模型）已受到许多学者的关注［4，133，134］，值得进一步研究和发展。微结构观察指出［10］，晶界位错通常具有复杂的伯格斯矢量（Burgers vectors），因而在描述晶界的动力学行为时应该考虑到这一点。

2.关于表观弛豫参量和内耗峰宽度

晶界内耗的弛豫参量是其动力学行为的表征。但是，晶界内耗的弛豫参量（例如H和τ0等）的物理意义往往难以从单一原子过程来理解（参见II.C.节）。近年来的研究指出，采用一种耦合模型或许可以帮助解决这个困惑的问题。

在III.D.节所述的耦合模型中，采用了一种非德拜（non-Debye）弛豫参数、代替通常采用的德拜（Debye）弛豫参数。考虑到晶界微观结构的复杂性和微量杂质的影响，在晶界内耗中可能有耦合效应发生，故采用这种耦合模型对晶界内耗数据进行了分析。根据这个耦合模型，表观激活能会因为耦合效应的增强而增高，不同类型晶界内耗的表观激活能的差别，可能是由于不同类型晶界中耦合效应的强度不同所引起。这些研究结果可以帮助解决多晶试样的晶界内耗中令人困惑的问题。

既然多晶试样中包含了不同类型的晶界，它的表观激活能实际上是不同类型晶界内耗激活能的平均值（或最可几值），应该依赖于晶界的特征分布（characteristic distribution）。在通常的多晶试样中，大角度无规倾侧晶界占有较大的比例。因而多晶试样的表观激活能往往与大角度无规倾侧晶界的相近。如III.D.节所述，后者中包含了中等程度的耦合效应，因而它的表观激活能稍高于晶界扩散的激活能。

关于晶界内耗峰的宽度，按照上述的耦合模型，峰宽应该随着耦合强度的增高而增宽。由于多晶试样中不同类型的晶界内耗峰各自的宽度不同，多晶试样中晶界内耗峰的宽度，是各个晶界内耗峰宽度叠加的结果。晶界类型的分布将导致内耗峰进一步展宽，因而多晶试样中晶界内耗峰的宽度一般大于双晶的晶界内耗峰的宽度，正如实验观察到的那样。

采用耦合模型对晶界内耗数据的分析，已经提供了一些新的信息。关于耦合模型的优越性和局限性，还值得做进一步研究。

V.结语和展望

（1）多晶、竹节晶和双晶试样的实验结果都证明了晶界内耗峰存在的事实。晶界内耗峰和相关的滞弹性效应可以很好地用滞弹性理论和粘滞性滑动模型加以解释。简单的说，内耗（能量损耗）是由晶界的粘滞性滑动引起的，而晶界滑动受到了某种结构单元的限制才使内耗峰能够出现。至于晶界内耗的微观机制，还有待进一步研究和发展。

（2）根据迄今为止的研究，经典的晶界粘滞性滑动模型中的某些假定需要加以修改或补充。例如，经典模型中曾假定多晶试样中的晶界滑动由于受到了晶界角的限制，才会出现内耗峰。但是，在没有晶界角的竹节晶和双晶试样也观察到了显著的晶界内耗峰。这说明限制晶界滑动的不仅有晶界角，而且还有其它的结构因素，如晶界中的“小面交界”（facet junctions）和位错网络等

（3）新近的研究表明，晶界内耗中有耦合效应（即多原子的关联运动）发生，而且不同类型的晶界中耦合效应程度不同。这就使得不同类型晶界内耗的表观激活能和内耗峰宽度有不同程度的增大。多晶材料中的晶界内耗激活能可以看成是不同类型晶界内耗的平均值（或最可几值），它依赖于试样中晶界类型的特征分布。多晶试样中晶界内耗峰的展宽可归因于不同类型晶界内耗峰叠加的结果。耦合模型的优越性和局限性值得进一步研究。

（4）发现晶界内耗的表观激活能与弛豫时间指数前因子之间存在“补偿效应”。这种补偿效应意味着晶界内耗的表观激活能与激活熵之间存在线性关系。因此，耦合效应不仅影响了表观激活能的数值，而且影响到激活熵的数值。

（5）晶界内耗已被有效地用来研究常规多晶材料中晶界的动力学行为、杂质在晶界的偏聚、以及晶界在形变过程中的演化等。而且晶界内耗也已经用来研究一些非常规多晶材料（如薄膜和超细晶材料）中晶界的稳定性和动力学行为。由于在双晶研究中发现不同类型晶界的表观激活参量不同，因而晶界内耗还有望用来研究不同类型晶界的“个性”，应用到“晶界工程”中去。

致谢

本文中双晶试样的制备和研究得到了德国亚琛大学G.Gottstein教授等的帮助和合作，耦合效应的分析得到了美国倪嘉陵（K.L.Ngai）教授的指教。本工作得到了中国自然科学基金委员会的连续支持（基金批准号：10274085，10674136，10804108，11274305，11274309），作者向他们表示衷心的感谢。

［1］Zener C.Elasticity and Anelasticity of Metals. Chicago Univ.Press，1948；中译本：金属的弹性与滞弹性.孔庆平，周本濂译，北京：科学出版社，1965

［2］Now ick A S，Berry B S.Anelastic Relaxation in Crystalline Solids.New York：Academ ic Press，1972

［3］冯端等.金属物理学（第三卷：金属力学性质）.北京：科学出版社，1999

［4］葛庭燧.固体内耗理论基础-晶界弛豫与晶界结构.北京：科学出版社，2000

［5］Blanter M S，Golovin IS，Neuhauser H，Sinning H R. Internal Friction in Metallic Materials-A Handbook. Berlin：Sp ringer，2007

［6］方前锋，金学军.内耗与力学谱基本原理及其应用.上海：上海交通大学出版社，2014

［7］M cLean D.Grain Boundaries in Metals.Oxford：Clarendon Press，1957；中译本：金属中的晶粒间界.杨顺华译.北京：科学出版社，1965

［8］G lieter H，Chalmers B.High Angle Grain Boundaries.Ox ford：Pergam on Press，1972

［9］Hirth J P，Lothe J.Theory of Dislocations.New Y-ork：John W iley&Sons Inc.，1982

［10］Sutton A P，Balluffi R W.Interfaces in Crystalline M aterials.Ox ford University P ress，2007

［11］Brandon D G.Acta M etall.，1966，14：1479

［12］Bruggeman G A，Bishop G H，and Hartt W H.in：The Nature and Behavior of Grain Boundaries（Hu H.Ed.），New York：Plenum Press，1972，83-122

［13］Pum ph rey P H.in：G rain Boundary Structure and Properties（Chadw ick G A，Sm ith D A.Eds.），London：Academ ic Press，1976，139-200

［14］Goodhew P J.in：Grain Boundary Structure and Kinetics（Balluffi R W.Ed.），Ohio：ASM，1980，155-176

［15］M yku ra H A.in：G rain Boundary Structure and K inetics（Ballu ffi R W.Ed.），Ohio：ASM，1980，445-456

［16］Gottstein G and Shvind lerm an L S.G rain boundary m igration in m etals：therm odynam ics，kinetics，applications.Boca Raton：CRC Press，1999

［17］Patala S，Mason J K，Schuh C A.Prog.Mater.Sci.，2012，57：1383

［18］W atanabe T.M ater.Sci.Eng.A，1993，166：11

［19］W atanabe T.G rain boundary engineering（a review）.J.Mater.Sci.，2011，46：4095

［20］Kˆe T S.Phys.Rev.，1947，71：533

［21］Kˆe T S.Phys.Rev.，1947，72：41

［22］Kˆe T S.Fifty-Year Study of G rain Boundary Relaxation（a rev iew）.M etall.M ater.Trans.，1999，A 30：2267

［23］Mott N F.Proc.Phys.Soc.，1948，60：391

［24］Kˆe T S.J.Appl.Phys.，1949，20：274

［25］Kˆe T S.J.App l.Phys.，1950，21：414

［26］Kˆe T S，Cui P，Su C M.Phys.Stat.Sol.（a），1984，84：157

［27］Iwasaki K.Phys.Stat.Sol.（a），1983，79：115

［28］Iwasaki K.Phys.Stat.Sol.（a），1984，81：485

［29］Cordea JN，Spertnak JW.Trans.A IME，1966，236：1685

［30］W illiam s T M，Leak G M.Acta Metall.，1967，15：1111

［31］Pearson S，Rotherham L.Trans.AIME.，1956，8：894

［32］Postnikov V S，Sharshakov I M，M aslemnikov Eh M.Relaxation Phenomena in Metals and A lloys（in Russian），M oscow：M etallurgiya，1963，165

［33］K¨oster W，Bangert L，Hafner J.Zeitschr.M etallk.，1956，47：224

［34］Morton M E，Leak G M.Acta Metall.，1966，14：1140

［35］Maier A K，M ari D，Tkalcec I，Schaller R.Acta Mater.，2014，74：132

［36］W ienig S，M ach lin E S.Trans.A IME，1957，209：32

［37］Roberts J T A，Barrand P.Trans.A IME，1968，242：2299

［38］.Kˆe T S.Trans.AIME，1948，176：448

［39］戢景文，魏全金，耿殿奇，吴玉琴.金属学报，1990，A 26：14

［40］王业宁，许自然，韩叶龙.物理学报，1966，22：647

［41］Schnitzel R H.J.Appl.Phys.，1959，30：2011

［42］Berlec I.Metall.Trans.，1970，1：2677

［43］Pratt JN，Bratina W J，Chalmers B.Acta Metall.，1954，2：203

［44］W inter J，W einig S.Trans.Metall.Soc.AIME，1959，215：74

［45］M iller D R.Trans.A IME，1962，224：275

［46］Bratina W J，W inegard W.C.Trans.A IME，1956，8：186

［47］Bangard t K，PreisendanzH.Zeitschr.Metallk.，1960，51：280

［48］Povolo F，Molinas B L.J.Nucl.Mater.，1983，114：85

［49］Esnouf C，Fantozzi G.J.Physique，1981，42-C5：445

［50］Hu X S，Zhang Y K，Zheng M Y，W u K.Scripta Mater.，2005，52：1141

［51］Hu X S，W ang X J，He X D，W u K，Zheng M Y. Trans.Non ferrous M et.Soc.China，2012，22：1907

［52］Jiang W B，Kong Q P，Magalas L B，Fang Q F. Archives Metall.Mater.，2015，60：371

［53］Postnikov V S，Sharshakov I M，M aslem nikov Eh M.Relaxation Phenom ena in M etals and A lloys（in Russian），M oscow：M etallurgiya，1963，p.165

［54］Rorberts G，Barrand P，Leak G M.Scripta M etall.，1969，3：409

［55］Kˆe T S.J.App l.Phys.，1948，19：285

［56］G ridnev V N，Kushnariva N P.in：Proceedings of the 9th International Con ference on Internal Friction and Ultrasonic Attenuation in Solids（Kˆe T S，Ed.），Oxford：Pergamon Press，1990，p.141

［57］Cao B，Schaller R，Benoit W，Cosandey F.J.A lloys Com pounds，1994，211-212：118

［58］Maier A K，Tkalcec I，M ari D，Schaller R.Scripta Mater.，2012，66：374

［59］Maier A K，M ari D，Tkalcec I，Schaller R.Archives M etall.M ater.，2015，60：377

［60］Bonetti E，Evangelista E，Gondi P，Tognato R.IL Nuovo Cimento B，1976，33：408

［61］Woirgard J，Riviere A，Fouquet J.J.Physique，1981，42-C5：407

［62］Riviere A，Am irau lt J P，W oirgard J.J.Physique，1981，42-C5：439

［63］N´o M L，Esnouf C，San Juan J，Fantozzi G.Acta Metall.，1988，36：827

［64］Molinas B J，Povolo F，Mater.Sci.Forum，1993，119-121：39

［65］Kˆe T S.J.Mater.Sci，Tech.，1998，14：481

［66］Yuan L X，Kˆe T S.Phys.Stat.Sol.（a），1996，154：573

［67］Kˆe T S，Zhang B S.Phys.Stat.Sol.（a），1986，96：515

［68］Cheng B L，Kˆe T S.J.Physique，1987；48-C8：413；Chinese Phys.Lett.，1988，5：81

［69］Kˆe T S，Zhang L D，Cheng B L，Zhu A W.Phys. Stat.Sol.（a），1988，108：569

［70］Zhu A W，Kˆe T S.Phys.Stat.Sol.（a），1989，113：393

［71］Xu T D，Cheng B Y.Prog.Mater.Sci.，2004，49：109

［72］Kˆe T S.J.App l.Phys.，1949，20：1226

［73］Kˆe T S，Kong Q P.Acta Physica Sinica，1954，10：365；Scientia Sinica，1955，4：55

［74］Wang Yening，Zhu Jinsong.J.Physique，1981，42-C5：457

［75］Kˆe T S，Cui P.Scripta M etell.M ater.，1992，26：1487

［76］Mori T，Koda M，M onzen R.Acta Metall.，1983，31：275

［77］Shi Y，Cai B，Kong Q P，Cui P，Gottstein G.J. M ater.Sci.，2003，38：1895

［78］Kˆe T S.Trans.AIME，1950，188：575

［79］颜鸣皋，袁振民.物理学报，1975，24：51

［80］孔庆平，常春城.物理学报，1975，24：168

［81］孔庆平，戴勇.物理学报，1987，36：855

［82］Kong Q P，Dai Y.Phys.Stat.Sol.（a），1990，118：431

［83］Dai Y，Liu S M，Kong Q P.Phys.Stat.Sol.（a），1990，118：K 21

［84］Kong Q P，Cai B，Gottstein G.J.M ater.Sci.，2001，36：5429

［85］Berry B.S，Pritchet W C.J.Physique，1981，42-C5：1111

［86］Bohn H G，Prieler M，Su C M，Trinkaus H，Schilling W.J.Phys.Chem.Solids，1994，55：1157

［87］Prieler M，Bohn H G，Schilling W，Trinkaus H.J. A lloys and Com pounds，1994，211/212：424

［88］Heinen D，Bohn H G，Schilling W.J.Appl.Phys.，1995，78：893

［89］Sosale G，A lm ecija D，Das K，and Vengallatore S. Nanotechnology，2012，23：155701

［90］Weller M，Dieh l J，Schaefer H E.Phil.M ag.A，1991，63：527

［91］W ang Y Z，Cui P，W u X J，Huang J B，Cai B.Phys. Stat.Sol.（a），2001，186：99

［92］Cai B，Kong Q P，Cui P，Cong H T，Sun X K.. Scripta Mater.，2001，44：1043

［93］Yung Z Q，Chen J，He L L，H.T.Cong，Ye H Q. Acta M ater.，2009，57：3633

［94］Bonetti E，Valdre G.Phil.Mag.B，1993，68：967

［95］Bonetti E，Del Bianco L，Pasquini L，Sam paolesi E. Nanostructured Materials，1998，10：741

［96］WeinsW N，M akinson JD，De Angelis R J，Axtell S C.Nanostructured M aterials，1997，9：509

［97］Valiev R Z，Estrin Y，Horita Z，Langdon T G，Zehetbauer M J，Zhu Y T.JOM，2006，58：33

［98］Golovin IS，Pal-Val P P，Pal-Val L N，Vatazzhuk E N，Estrin Y.Solid State Phenomena，2012，184：289

［99］Fan G D，Zheng M Y，Hu X S，Xu C，W u K，Golovin IS.Mater.Sci.Eng.A，2012，566：588

［100］Gunderov D V，Polyakov A V，Sitdikov V D，Churakova A A，Golovin IS.The Physics of Metals and M etallgraphy，2013，114：1078

［101］Guan X S，Kˆe T S.J.A lloys and Com pounds，1994，211/212：480

［102］Shi Y，Cui P，Kong Q P，Jiang W B，W inning M. Phys.Rev.B，2005，71：R060101

［103］Jiang W B，Cui P，Kong Q P，Shi Y，W inning M. Phys.Rev.B，2005，72：174118

［104］Shi Y，Jiang W B，Kong Q P，Cui P，Fang Q F，W inning M.Phys.Rev.B，2006，73：174101

［105］孔庆平，崔平，蒋卫斌，石云，方前锋.物理学进展，2006，26：277

［106］Kong Q P，Jiang W B，Shi Y，Cui P，Fang Q F，W inning M.Mater Sci Eng.A，2009，521-522：128

［107］Jiang W B，Kong Q P，M olodov D A，Gottstein G. Acta Mater.，2009，57：3327

［108］Jiang W B，Kong Q P，Cui P，Fang F Q，M olodov D A，Gottstein G.Phil.Mag.，2010，90：753

［109］Jiang W B，Kong Q P，Cui P.Mater Sci Eng.A，2010，527：6028

［110］Kong Q P，Jiang W B，Cui P，Fang Q F.，Solid State Phenomena，2012，184：33

［111］Raj R，Ashby M F.M etall.Trans.，1971，2：1113

［112］Ngai K L.Relaxation and Diffusion in Com plex Systems.New York：Sp ringer，2011

［113］Ngai K L，W ang Y N，M agalas L B.J.A lloys Com ps.，1994，211/212：327

［114］Wang Y N，Gu M，Sun L H，Ngai K L.Phys.Rev. B，1994，50：3525

［115］Wang X P，Fang Q F.Phys.Rev.B，2002，65：064304

［116］Guo L J，W u X B，Zhu Z G.J.A pp l.Phys.，2011，109：113524

［117］Gottstein G，Shvind lerman L S.Interface Sci.，1998，6：265

［118］Molodov D A，Czubayko U，Gottstein G，Shvindlerm an L S.Acta M ater.，1998，46：553

［119］Surholt T，M olodov D A，Herzig C.Acta Mater.，1998，46：5345

［120］Peacock-L´opez E，Suh l H.Phys.Rev.B，1982，26：3774

［121］Lejcek P，Hofm ann S.C ri.Rev.in Sol.State M ater. Sci.，2008，33：133

［122］Zener C.Phys.Rev.，1941，60：906

［123］Ham ilton JC，SiegelD J，Daruka I，Leonard F.Phys. Rev.Lett.，2003，90：246102

［124］Jin Q，Chan SW.J.M ater.Res.，2002，17：323

［125］Sigle W，Chang L S，Gast W.Phil.Mag.A，2002，82：1595

［126］Ashmarin G M，Zhikharev A I，Shvedov Y A.IX Con ferencija M etaloznaw cka PAN（T raszkow ski V. Ed.）K rakow，1977，391-400

［127］Shvedov Y A.Scripta Metall.，1979，13：801

［128］Ashmarin G M，Zhikharev A I，Shvedov Y A.in：Proc.9th Inter.Con f.on Internal Friction and Ultrasonic A ttenuation（Kˆe T S，Ed.），Ox ford：Pergam on Press，1990，p.137

［129］Sun Z Q，Kˆe T S.J.Physique，1981，42-C5：451

［130］Sun Z.Q.in：Proc.9th Inter.Con f.on Internal Friction and Ultrasonic Attenuation（Kˆe T S Ed.），Oxford：Pergam on P ress，1990，p.121

［131］Darinskii B M，Kalinin Y E，M ush tenko S V，Sa jko D S.Solid State Phenomena，2003，89：203

［132］Darinskii B M，Kalinin Y E，Sa jko D S.Solid State Phenomena，2006，115：73.

［133］Benoit W.in：M echanical Spectroscopy，M aterials Science Forum，Sw itzerland：Trans.Tech.Pub lications，2001，366-368：306

［134］Benoit W.Mater.Sci.Eng.A，2004，370：12

Internal friction（or dam ping）is am easure of energy d issipation du ring m echanical vib ration. The internal friction peak induced by grain boundary（GB）relaxation was discovered by Kˆe in polycrystals in 1947 by using his invented“Kˆe pendu lum”.The GB internal friction and related anelastic effects can be successfully interpreted in term s of Zener's anelastic theory and viscous slid ingm odel.Since then，the GB internal friction peak hasbeen w idely used to study the dynam ic p rocess of GBs，im pu rity segregation at GBs and relevant p rocesses in m aterials science.

Previously，the GB internal friction was mostly studied w ith polycrystalline materials，in which m ixed contributions of different types of GBs are involved.Since them icrostructures and behaviors of different types of GBs are different，such internal friction can on ly reveal the general behaviors of GBs，w hile the detailed m echanism of the GB peak in polycryatals is hard ly clarified.

From the beginning of the 21th centu ry，the internal friction in bicrystals（each has a single boundary）has been systematically investigated.The resu lts indicate that the internal friction can be used to distinguish the individual behavior of different types of GBs and applied to the p ractice of“GB design and control”（or“GB engineering”）.Moreover，the coup ling effect and com pensation effect involved in GB relaxation has been recently revealed and exp lained.These find ings im p rove the understand ing of them echanism of GB internal friction.

The p resent paper attem p ts to give a com p rehensive review to the investigations of GB internal friction in polycrystals，bamboo-crystals and bicrystals.The m icroscopic mechanism s and the further app lications of GB internal friction are discussed and p rospected.

date：2016-04-05

Progress in the Investigations of Grain Boundary Internal Friction

Kong Qing-Ping∗，Fang Qian-Feng，Jiang Wei-Bin，Cui Ping
Key Laboratory of Materials Physics，Institute of Solid State Physics，Chinese Academy of Sciences，Hefei230031，China

Internal friction；G rain boundary；Polycrystal；Bam boo-crystal；B icrystal；Coup ling effect；Com pensation effect

O 487

A

10.13725/j.cnki.p ip.2016.02.002

*E-m ail：qpkong@issp.ac.cn

1000-0542（2016）02-0046-18 46