选例题要“一题多解” 做习题求“多题一解”——谈毕业总复习阶段“组合图形的面积计算”的复习策略
浙江杭州市萧山区楼塔镇岩山中心小学(310000) 章中其
选例题要“一题多解”做习题求“多题一解”——谈毕业总复习阶段“组合图形的面积计算”的复习策略
浙江杭州市萧山区楼塔镇岩山中心小学(310000)章中其
教师应摒弃以往“就题论题”的复习方法,引导学生把组合图形的面积计算归入知识系统后进行深入的探究,使学生体会到“合并求和”“去空求差”的数学思想方法,促进学生思维的发展。
一题多解多题一解合并求和去空求差思想方法
在课堂教学中,为了开拓学生的解题思路,培养和提高学生思维的广阔性、灵活性,教师往往会采用“一题多解”的例题。“一题多解”的讲解和训练,不仅可以使师生加深对题旨的理解,而且可以促进学生明晰题中的数量关系,寻求到更合理、更简捷的解题方法。如在毕业总复习阶段复习“组合图形的面积计算”时,我按照传统的“一题多解”的方法,让学生自我总结“万变不离其宗”的思想方法,变“一题多解”为“多题一解”,使学生的解题能力得到提高。
一、选例题时要“一题多解”,使学生掌握思想方法
罗增儒认为:“分析典型例题的解题过程是学会解题的有效途径,至少在没有找到更好的途径之前,这是一个无以替代的好主意。”因此,在毕业班总复习阶段复习“组合图形的面积计算”时,我采用不同的方法分割图形,使学生在“一题多解”中自主归纳自己的解题策略,反思正误、总结经验,领悟和掌握解题的思想方法。
例:如右图,算出图形阴影部分的面积。

在动手解题前,对图形进行仔细的观察和初步的分析是十分必要的,有利于我们进一步分析题意、确定思维方法和找到解题路径。题中的图形由一个三角形和一个半圆组成,阴影部分由三角形的两边和半圆周的一部分围成,这个三角形的一个角是直角,一个锐角是45°,由“三角形内角和等于180°”可以求出另一个锐角的度数,说明这个三角形是等腰直角三角形。
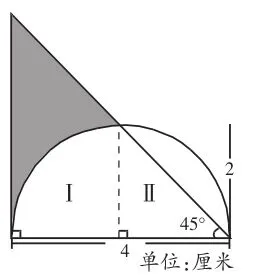
解法1:如右图,很明显,阴影部分面积等于这个直角三角形面积减去半圆在三角形内的部分面积,因为两直角边是已知的,容易求得直角三角形的面积,现在关键在于求出半圆在直角三角形内部分的面积。为此目的,可以通过圆心和半圆周与直角三角形斜边的交点画一条辅助线,这样就把半圆在三角形内部的部分分割成两部分,即这个圆的和一个小直角三角形,然后在图上分别用Ⅰ和Ⅱ来表示,于是问题得到解决。


解法3:如右图,连接两点间的线段,可以看出这条线段正好把这个直角三角形平均分成了两部分(想一想,为什么),阴影部分的面积正好可以由这样分得的直角三角形的一半减去弓形面积求出,这里弓形面积显然和解法2中的弓形面积是相等的。这个分析过程可用下面的示意图表示:

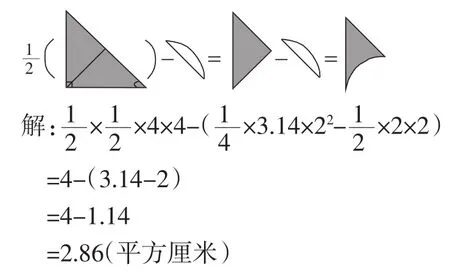
解法4:如右图,与解法1相同,把圆心和三角形斜边与圆周的交点连接起来,则这条线段一定平行于这个直角三角形的一条直角边,这样就得到了一个梯形,梯形的上底是圆的半径,也就是这个直角三角形直角边(即圆的直径)的一半,下底是这个直角三角形的一条直角边,高也是圆的半径,所以阴影部分的面积就是这个梯形的面积减去这个圆的这个分析过程可以用下图来表示
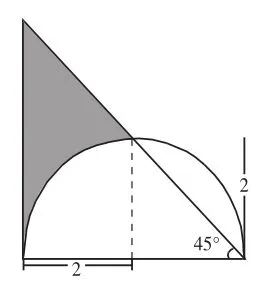

纵观以上四种不同的解法,让学生一边看图示,一边总结,使学生首先领悟到无论哪一种解法都是“大图形”减去“小图形”。然后我出示以下两个图形,让学生明确其一、其二都属于组合图形的面积计算,其一是“图形加法”,用“合并求和”解决;其二是“图形减法”,一般求阴影部分的面积用“去空求差”计算。

此外,组合图形的面积计算有时也会用以下两种方法解决:一是平移转换。在计算阴影部分面积时,可以用移动变换图形的方法求解。如右图,通过平移,使我们明了阴影部分面积占正方形面积的二是旋转变换,在看图计算中应用比较广泛。如下图,通过旋转阴影部分,使我们的解题思路豁然开朗。
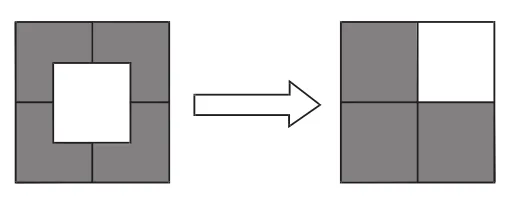

二、做习题时求“多题一解”,促进学生自主掌握解法
我教毕业班已有十多届,以往喜欢在毕业总复习阶段寻找几张练习卷,让学生重复训练《单元卷》《习题卷》,因涉及图形的种类比较多,所以学生的训练量比较大,情绪比较抵触,效果也不明显。近几年,我摒弃以往重复、低层次练习的做法,选用经典例题,通过归类训练,让学生自悟数学思想方法,其效果的确比较理想。
例如,在进行“一题多解”的经典例题教学后,我出示以下三组练习,让学生能独立解决的先独立解决,但解决前要说说解决问题的策略是什么,如有什么疑问可以向同桌请教或与同组成员进行讨论交流。
第一组:求下列图形中阴影部分的面积。(单位:厘米)
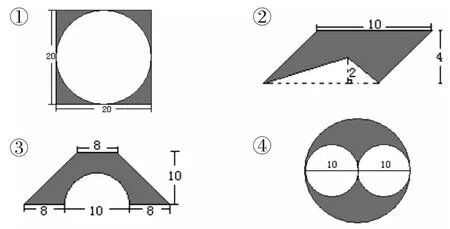
本题组训练,涉及的图形几乎包含了小学阶段所有的平面图形,由于图形的数据比较简单,且学生对于每一个图形的计算公式均已牢记,所以学生列式计算的正确率达到100%。训练后得出结论:原来这些题的解题策略都是“大图形减去小图形”(即‘去空求差’),关键是要明确求阴影部分的面积时,主要是由哪几个基本图形去减。
第二组:求下列图形中阴影部分的面积。(单位:分米)

本题组训练,学生单独解决的错误率比较高:图①的主要问题是受例题的负迁移影响,部分学生计算时漏掉了弓形的面积,部分学生按照例题的解决方法来做,算式比较长,计算容易出现错误;图②的主要问题是一部分学生看到图形比较复杂,一时找不到方法解决。但在训练过程中,有相当一部分学生利用旋转和翻转的方法,轻松、快速地解决问题,并且发现了图①和图②之间的联系(一分为二)与区别(拼成了平行四边形或长方形,计算更简单)。通过交流反馈,学生恍然大悟——原来“去空求差”中可以利用平移、旋转等方法使解题策略更简单,感受到了数学思想方法的魅力。
第三组:
①如图A,求图形的面积(单位:厘米)。
②如图B,求阴影部分的面积和周长(单位:厘米)。
本题组训练,图①的难度不大,主要涉及“合并求和”的思想方法,学生都能够掌握;图②涉及周长的概念,学生对阴影部分的周长概念模糊,不清楚该图形的周长应该包括哪几部分,有些学生则漏掉了圆的周长部分。而且,图B的面积部分更复杂,若是按照常规方法来解决,计算会很复杂,但学生的列式正确率还是比较高的。通过交流反馈,学生对于图B的解题策略很令人欣慰:其一,周长采用类似于图A面积计算“合并求和”的策略,用“正方形的周长+圆的周长×2”来解决;其二,计算面积的解决方案就更精彩了,特别是有学生利用“正方形内最大圆占其面积的78.5%,剩余部分占21.5%”的规律来解决问题,令人既意外又开心。

图A
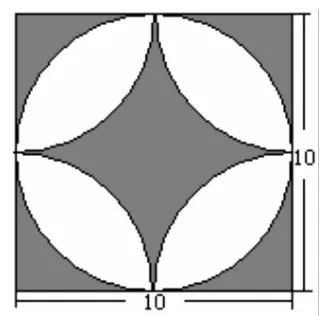
图B
科学哲学家库恩认为:“学生是通过范例、习题等来掌握一门科学知识及其方法的,没有范例,科学知识就不能清楚地表达出来,也无法为人们所掌握;没有范例,人们也无法按照该门科学的要求去解决任何问题,数学也不例外。”因此,教师应摒弃以往“就题论题”的复习方法,引导学生把组合图形的面积计算归入知识系统后进行深入的探究,使学生体会到“合并求和”“去空求差”的数学思想方法,促进学生思维的发展。
(责编蓝天)
G623.5
A
1007-9068(2016)29-026

