Massive MIMO多用户系统波束成形的凸优化解决思路分析*

何 华，姜 静

（西安邮电大学 通信与信息工程学院，陕西 西安 710121）

Massive MIMO多用户系统波束成形的凸优化解决思路分析*

何 华，姜 静

（西安邮电大学 通信与信息工程学院，陕西 西安 710121）

在Massive MIMO多用户通信系统中，波束形成利用空分的思想来调整多波束的方向相位，使得各波束对用户的指向更精确，从而有效提高系统的能效。波束算法最终要解决某一类优化问题，传统方法常常使用迭代计算，不但收敛速率慢，停止条件难以明确，且常常只能计算出局部最优值。因此，提出将凸优化理论与方法应用到Massive MIMO多用户通信系统中进行波束成形计算的思路，以大大加快计算收敛速率，且局部最优一定是全局最优，使得波束优化问题得到快速、可靠解决。

大规模多输入多输出；凸优化；波束形成；收敛速度

0　引 言

凸优化方法被广泛应用于多种科学问题的设计和分析，特别是在通信与信号处理方面，凸优化应用解决了一些其他方法难以解决的问题，因而成为一种重要的方法和途径，值得研究者不断学习［1］。凸优化方法还被用来有效与可靠地解决大型的、实际的工程问题。它提供了非传统计算和数学方法，解决了实际中更为复杂的问题［2］。

为什么凸优化方法可以解决通信中的许多问题？归根结底是因为许多通信问题可以被定义为凸优化问题，或者可以转化为凸优化问题。这也体现

出凸优化在通信领域的应用不容忽视［3］。

凸优化是凸目标函数的最小化，且必须满足

某种凸的限制条件。认识凸优化问题可以从三个方面入手。首先，能够将某一科学问题表示成优化问题；其次，判断优化问题是否为凸优化问题；第三，对判断的凸优化问题利用凸优化方法进行分析与计算［4］。如果某一个科学问题可以被表示为凸优化问题，那基本可以确定此问题已经得到了解决。

1　优化问题

优化问题是指具有形如式（1）的形式［5］：

其中，x是优化变量，f0是代价函数，fi和hi分别是不等式约束和等式约束。式（1）可理解为在同时满足fi（x）≤0，i=1，…，m和hi（x）=0，i=1，…，p条件的x集合中找出最小化f0（x）的点x*，并求出f0（x*）的值。

一般来说，形如这样的问题用一般的传统方法很难解决。原因归结起来有三点：第一，当x维数较大，该问题会变得非常复杂；第二，收敛速率较慢是优化问题难以解决的极大障碍，常常在迭代计算进行了很多次后，仍然难以找到可行的最优解；第三，迭代停止的标准较为武断，在迭代计算停止时，或许找到的最优解只是局部最优解，但此时若满足停止条件，则会将局部最优解当作全局最优解来使用，从而在很大程度上降低了优化问题解的正确性与可靠性。因此，凸优化方法越来越成为当今很多领域的重要解决途径。

2　凸优化问题

如果能将某个问题表述为凸优化问题，那么就能迅速有效地进行求解。使用凸优化的难点或技巧，在于如何判断某个问题是否为凸优化问题。一旦实际问题成功被表述为凸优化问题的形式，那么解决该问题将只是一项技术问题［6］。

凸优化问题具有形如式（2）的形式［7］：

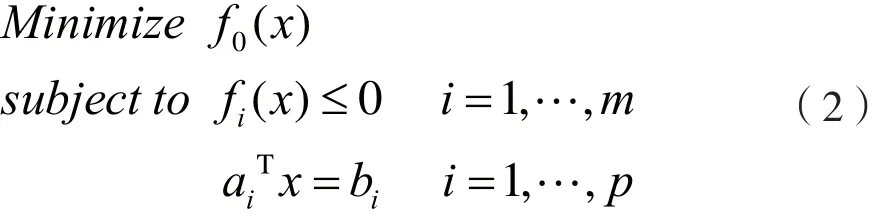
其中，x是优化变量，f0是代价函数，fi和分别是不等式约束和等式约束。将凸优化表达式（2）与一般优化表达式（1）进行比较发现，需满足以下三个条件，才可将该优化问题称之为凸优化。第一，代价函数（也称目标函数）必须是凸的；第二，不等式约束函数必须均是凸的；第三，等 式约束函数必须是 仿射的，即式（1）中的hi须具有的形式，且对于成立。

3　Massive MIMO多用户通信系统下行波束成形的凸优化解决思路

波束成形是Massive MIMO多用户通信系统中解决用户间干扰、提高能量效率和频谱效率的有力途径。考虑一个配有N根天线的单基站通信系统，共有M个用户，每个用户具有1根天线，如图1所示。

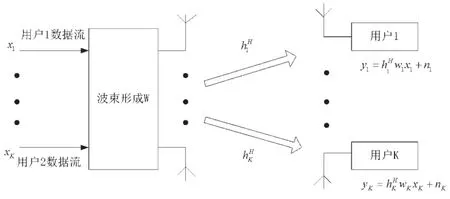
图1　多用户Massive M IMO通信系统

基站的发送信 号可如 式（3）所示：

其中，xm为向用户m传送的发射信号，wm为用户m的波束向量。

用户m的 接收信号可表示为：

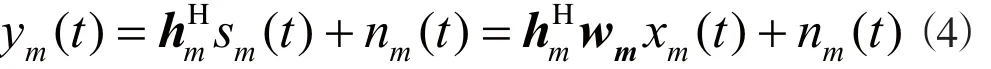
下行波束成形优化问题中，有三种情况是波束成形算法常常需达到的优化标准。

第一，限制每个用户的接收信干噪比SINR（Signal Interference Noise Rate）必须达到一定水平，同时最小化发射总功率。该SINR平衡问题可表示为：

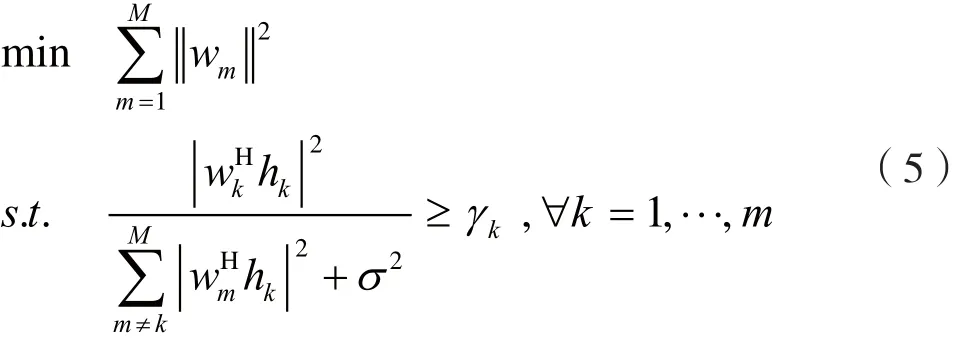
其中，γk是用户K需要接收的最小SINR。

第二，下行波束成形还可以考虑 信漏噪比S LNR（Signal Leakege Noise Rate）。用户m的信号泄漏到其他用户的比例需限制在一定的水平上：

其中，βk是用户K必须满足的最小SLNR。

第三，当发射功率的大小有限制时，发射功率的限制则变为约束条件，而同时要满足此约束下用户端能够达到最大的信干噪比或信漏噪比：

式（5）、式（6）和式（7）均是多用户Massive MIMO通信系统中波束成形常遇到的优化问题。解决这些优化问题的传统方法是迭代算法，但是迭代算法的收敛速率慢，停止条件模糊，常常计算不出最优值，或仅仅只能计算出局部最优值。然而，如果采用凸优化的方法，只要能计算出局部最优值，则可确定该值即是全局最优。因为凸优化的基本性质就是其任意局部最优解也是全局最优解。

但是，以上考虑的三种优化问题均不是凸优化问题，因此需要打破传统迭代算法的思路，将波束成形的三种优化问题利用凸优化的理论知识转换成凸优化问题，或在一定程度上降低约束条件，使得非凸优化问题转化为凸优化问题，然后再用凸优化方法，如拉格朗日法、KKT条件法、Newton法或内积等方法来进行求解，最终使得优化问题得以可靠、快速解决。

4　结 语

本文说明了迭代算法在凸优化算法中的不足，提出了用凸优化方法来解决波束形成问题的思路，以期改善迭代算法带来的收敛速率慢、局部最优等问题，最终提高Massive MIMO多用户通信系统的性能。

［1］ Gershman A B，Sidiropoulos N D，Shahbazpanahi S，et al.Convex Optimization-Based Beamforming［J］.IEEE Signal Processing Magazine，2010，27（03）：62-75.

［2］ Chang T H，Luo Z Q，Chi C Y.Approximation Bounds for Semidefinite Relaxation of Max-Min-Fair Multicast Transmit Beamforming Problem［J］.IEEE Transactions on Signal Processi ng，2008，56（08）：3932-3943.

［3］ WEI Yu，TIAN Lan.Transmitter Optimization for the Multi-Antenna Downlink With Per-Antenna Power Constraints［J］.IEEE Transactions on Signal Processi ng，2007，55（06）：2046-2660.

［4］ Lingbing Hu，Hongwei Liu，Da-Zheng Feng，et al.Optimal Mismatched Filter Bank Design for MIMO Radar via Convex Optimization［C］.IEEE Internation al Conference on Waveforms Diversity and Design，2010：126-131.

［5］ 孙波.多天线系统的波束成形技术研究［D］.成都：西南交通大学，2009.

SUN Bo.Beam Forming Technology of Multi Antenna System［D］.Chengdu：Southwest JiaoTong University，2009.

［6］ Boyd S，Vandenberghe L.Covex Optimization［M］.New York：Ca m-bridge University Press，2004.

［7］ 宁英井.基于凸优化的鲁棒认知波束形成技术［D］.哈尔滨：哈尔滨工业大学，2013：15-17.

NING Ying-jing.Robust Cognitive Beam based on Convex Optimization Technique［D］.Harbin：Harbin Institute of Technology，2013：15-17.

何 华（1982—），女，博士，讲师，主要研究方向为无线通信；

姜 静（1974—），女，博士，教授，主要研究方向为无线通信。

Convex Optimization Solution of Beam Forming in Massive MIMO

HE Hua， JIANG Jing
（Faculty of Communication and Information Engineering， Xi'an University of Telecommunications and Posts， Xi'an Shaanxi 710121， China）

In Massive MIMO multiuser communication system， beamforming adjusts the directions of multiple beams， and makes these beams more accurately point to the users， thus effectively improving the energy efficiency of the system. Beamforming algorithm ultimately solves a certain class of optimization problems， and the traditional methods often use iterative calculation. However， this iteration is slow in convergence rate and indistinct in stop condition， and usually calculates the local optimal value only. For this reason， the convex optimization theory and methods are proposed and applied to the massive MIMO multiuser communication system for beamforming calculations， thus to greatly accelerate the convergence rate and ensure that the local optimum must be the global optimum， and finally make a rapid and reliable solution of beamforming optimization problem.

Massive MIMO； convex optimization； beamforming； convergence rate

Scientific Research Plan Projects of Shaanxi Education Department（No.16JK1688）

TN929.12

A

1002-0802（2016）-10-1317-03

10.3969/j.issn.1002-0802.2016.10.010

2016-06-14；

2016-09-19

data：2016-06-14；Revised data：2016-09-19

陕西省教育厅专项科研计划项目（No.16JK1688）