无黏性颗粒对竖直推土板阻力影响的连续介质模型

郭　鸿，骆亚生，陈　茜，程大伟

(1 陕西理工大学 土木工程与建筑学院，陕西 汉中 723001；2 西北农林科技大学 水利水电科学研究院，陕西 杨凌 712100；3 长安大学 环境科学与工程学院，陕西 西安 710064)



无黏性颗粒对竖直推土板阻力影响的连续介质模型

郭鸿1,2，骆亚生2，陈茜1，程大伟3

(1 陕西理工大学 土木工程与建筑学院，陕西 汉中 723001；2 西北农林科技大学 水利水电科学研究院，陕西 杨凌 712100；3 长安大学 环境科学与工程学院，陕西 西安 710064)

【目的】 基于改进库伦被动土压力理论，研究不同运动速度和侵入深度情况下无黏性离散颗粒对竖直推土板的阻力影响规律。【方法】 采用改进的带翼刚性竖直推土板进行室内物理力学试验，分析不同侵入深度(2，3和4 cm)和推动速度(1，0.5 cm/s)下无黏性离散颗粒对竖直推土板阻力的影响规律，采用数值模拟的方法建立相应的离散元模型，分析离散颗粒在推土板作用下剪切带的变化规律。【结果】 室内试验表明，侵入深度为2，3，4 cm时推土板的计算位移分别为0.15，0.11和0.08 m，阻力增量分别为3.4，2.5和4.1 N，增长率分别为22.7，22.7和51.3 N/m。在相同情况下，推动速度对阻力的影响不明显。数值试验表明，因推土板推移而产生的剪切带与相对水平方向存在一个典型倾角，该倾角随位移变化。根据剪切带的变化规律和惯性数的分布规律，提出了预测推土板所受阻力的数学模型。【结论】 实例验证表明，所建立的连续介质模型能很好地预测无黏性离散颗粒对竖直推土板所产生的阻力，且精度较高。

推土板；无黏性离散颗粒；颗粒流；推动阻力；改进库伦模型

推土板在农业工程中应用十分广泛，比如土壤耕作、谷物晾晒等。从当前正在流行的颗粒流观点来看，推土板在离散颗粒中运动所涉及的问题属于推土板激发颗粒流的范畴，推土板激发颗粒流的研究近年来受到国内外学者的重视[1-16]。从颗粒物质力学的角度看，与普通的平面颗粒流不同，推土问题属于复杂的颗粒流行为。因此，对于离散颗粒作用在推土板上的阻力而言，既不能用传统的连续介质力学理论描述，也不适合用经典的平面颗粒流理论来描述。Science将能否建立颗粒材料运动学的综合理论列为当今世界上最前沿的125个问题之一[17]。

作为一种特殊的推土板激发颗粒流，推动阻力(即推土板运动时所受的阻力)的数学表达是问题的关键所在。尽管文献[8]对推土板的表面形态及土颗粒的动态行为进行了研究，但是推土板速度对阻力的影响并未涉及。Percier等[13]对于推土板激发的复杂颗粒流也有相应的研究，但其不足之处在于并未考虑位移、速度以及边界效应的综合影响。虽然已有关于简单重力式或者整齐剪切式颗粒流的相对成熟的宏观理论[18]，然而用这种理论很难描述推土板扰动的复杂颗粒流行为。文献[19]对竖直推土板激发的颗粒流连续模型也仅在小位移方面做了探讨，其是否适用于大位移情形尚需进一步研究。基于此，本研究综合考虑位移、边界条件以及速度效应，并借鉴库伦被动土压力理论，拟探讨建立一种能够预测推土板在土壤中所受阻力的宏观模型，进而

为推动阻力的预测提供支持。

1　室内物理试验

1.1试验装置

图1所示是薄板推土板实体模型的平面示意图。在推土板的两边设置了1对约束翼，其目的就是为了约束颗粒向垂直于颗粒流动的方向溢出，保证物理试验中的颗粒流动方向和推土板运动方向一致。这种将颗粒流动方向控制成平面上直线流动的颗粒流，可以看作是二维流态。试验采用直径为(5±1) mm(即不均匀率为20%)的玻璃珠模拟土颗粒，颗粒密度为2 550 kg/m3。室内物理试验参数如表1所示。其中密实度φ是颗粒体积与总堆积体积的比值，其值(0.61)对应的相对密度(0.48)与二维离散元保持一致。

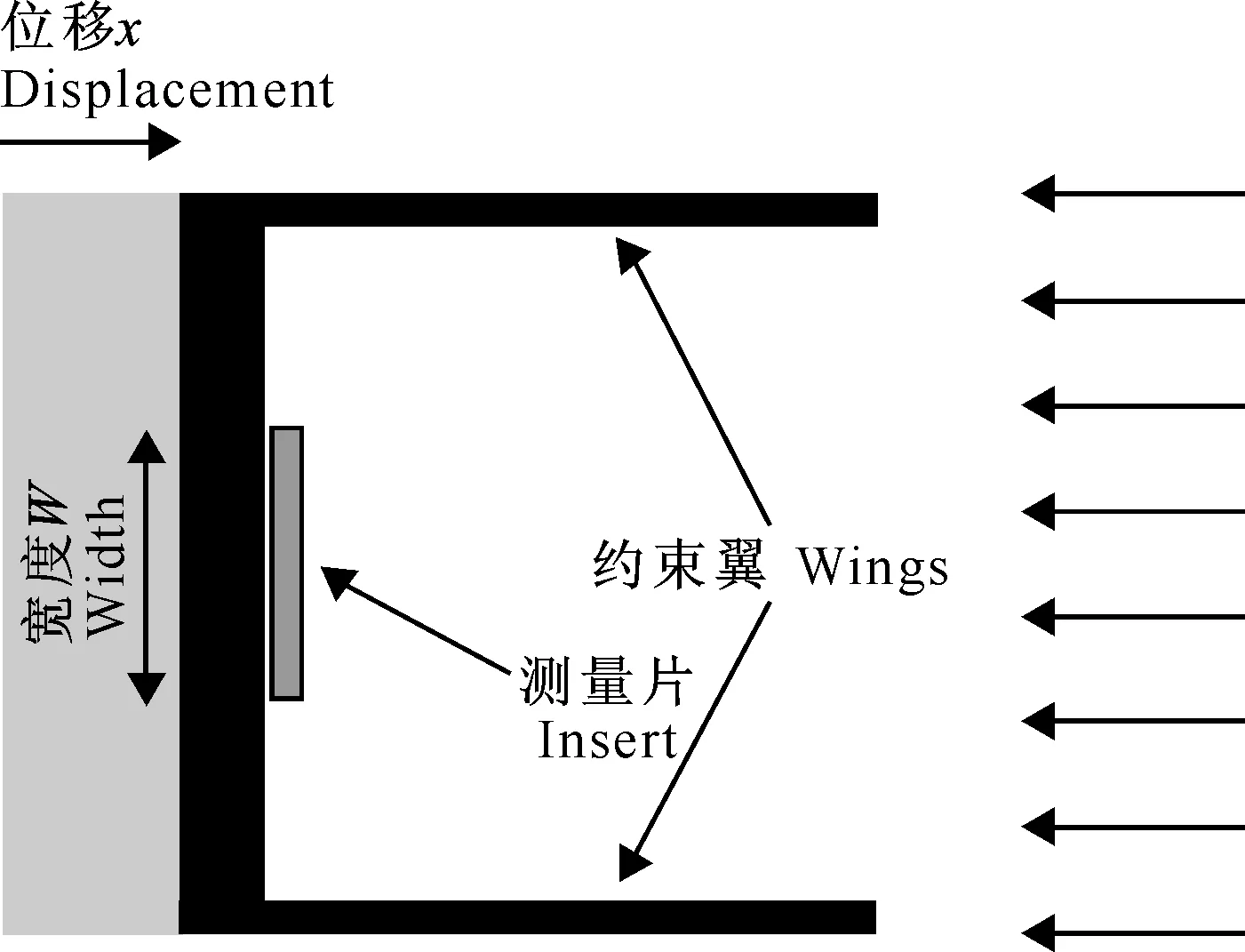
图 1　推土板室内试验装置示意Fig.1　Schematic diagram of indoor experimental apparatus of bulldozing plate

表 1　推土板室内物理试验参数Table 1　Experimental parameters for indoor physics tests

物理试验中采用2种不同的水平推动速度，即0.5和1 cm/s。由于室内物理试验中使用的推土板应力感应部分高度有限，因此均采用数值较小的侵入深度，即2，3和4 cm。同时，推动距离也需随着侵入深度的增加而减小，否则推土板前方的颗粒堆积就会超过应力感应器的适用范围。经过多次试验发现，室内的推动速度小于1 cm/s时数据的噪音较小。本研究的各组物理试验都进行了21次平行试验，最终结果取所有平行试验的平均值。

1.2试验结果

图2为2个推动速度和3个侵入深度下阻力 与位移x的关系散点图。由图2可以看出，3种不同侵入深度(2，3和4 cm)下推土板的计算位移分别为0.15，0.11和0.08 m，阻力增量分别为 3.4，2.5和4.1 N，增长率分别为22.7，22.7和 51.3 N/m。说明当侵入深度比较大时，阻力的增长变快。另外，在相同侵入深度下，推动速度对阻力的影响不明显。需要说明的是：1)该曲线舍去了初始5 cm位移时的数据和结束前2 cm的数据，这是因为该段数据噪音异常，原因应该是推土板在实际物理试验中的最初阶段呈加速运动，在最终阶段呈减速运动；2)非匀速运动暂时不在本试验的研究范围内。

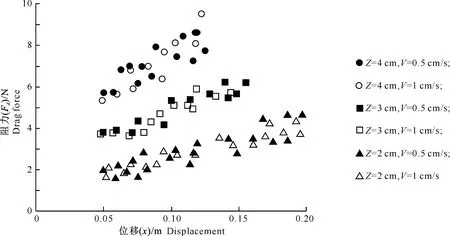
图 2　不同推动速度和侵入深度对推动板所受阻力的影响Fig.2　Effect of velocity and immersion depth on drag force

2　二维颗粒离散元模拟

2.1颗粒离散元模型的建立

竖直推土板激发的颗粒流是最简单也是很重要的一类扰动式颗粒流动。然而，室内物理试验无法得到剪切滑动面上的法向力以及剪切力，为了从微观方面深入了解由推土板运动而形成的剪切带，本研究采用颗粒离散元模型进行数值模拟。数值试验采用直径5 mm的圆盘模型，具体参数如表2所示。

表 2　颗粒离散元数值模拟参数Table 2　Numerical simulation parameters for particulate DEM

二维数值试验参数(表2)中，颗粒直径为实际颗粒直径的2倍，不均匀率、颗粒密度与原颗粒相同，二维孔隙率16%代表其相对密度为0.48，墙体刚度为颗粒刚度的10倍，局部阻尼采用动态模拟的建议值，黏性阻尼通过测定实际颗粒在自由落体中的弹跳运动确定。

采用二维颗粒(圆盘)离散元模拟三维颗粒(圆球)，同一颗粒体系不同维数下其颗粒孔隙率和密实程度是相异的。因此借鉴土力学的思想，利用相对密度的概念，将三维条件下的相对密度和二维条件下的相对密度联系起来，有：

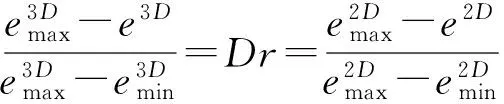
(1)

式中：e为孔隙比，2D和3D分别表示二维和三维，max和min分别表示最大和最小，Dr为相对密度。

密实度φ(Packing fraction)与孔隙比的关系可以表示为：

e=(1-φ)/φ。

(2)

因此，可以得到：

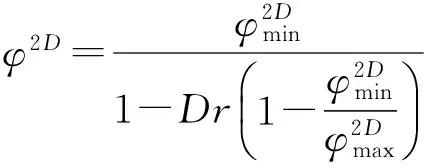
(3)

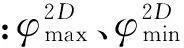
2.2剪切带的变化规律

推土板推动土壤的颗粒流初始模型如图3-A所示。随着推土板水平向右运动，其前方随之形成颗粒堆起(图3-B)。

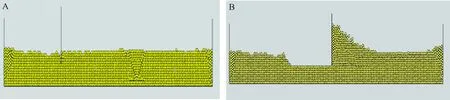
图 3　推土板工作中的二维颗粒离散元模型示意图Fig.3　2D model for particulate DEM

图4是3种不同推土板位移(x=5d，7d和10d，d为颗粒直径)下颗粒的位移场，可以看出在推土板的作用下，颗粒的位移场表现为明显的楔体形态，且剪切带相对水平方向的倾角随位移而变化。基于此，假设存在一个典型倾角θ0，且楔体分为2部分，一部分是推土板推动作用形成的颗粒堆积，另一部分是颗粒床中受剪的楔体部分。当上部堆积比较少时(图5-A)，剪切带的方向由典型倾角控制(不妨称为典型剪切带)；当上部堆积的尾部与典型剪切带恰好相交时，剪切带的倾角即随着上部堆积的移动而减小，随后的过程始终保持与上部堆积的尾部相交(图5-B)。

图 4颗粒位移场随推土板位移x的变化

Fig.4Displacement field of particles changing with the displacementxof bulldozing plate

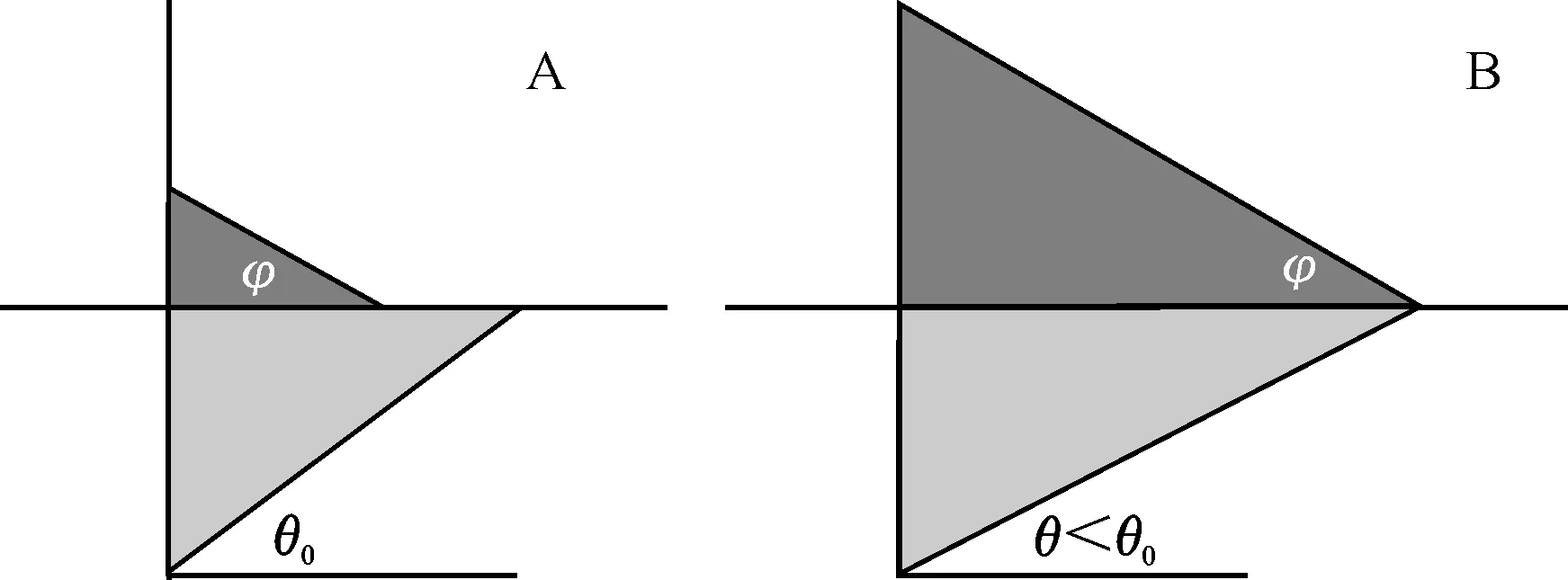
图 5　颗粒初始状态和平衡状态时的楔体形态Fig.5　Wedge shape of initial and equilibrium states of particles

2.3广义摩擦系数和广义摩擦角

根据惯性数观点[1,7]确定本研究颗粒流的流态。惯性数(无量纲)的表达式为：

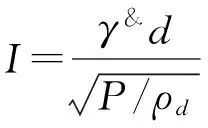
(4)

式中：γ&为剪切速率，d为颗粒直径，P为压应力，ρd为颗粒密度。当I≤10-3时，流态为准静态流；10-310-1时为碰撞流。以推动速度为0.1 m/s，位移为10d作例，用惯性数的概念计算出惯性数在二维颗粒床上的分布如图6所示，为了使惯性数的分布更易于分辨，图6中采用了惯性数的对数值。从图6可以发现，大部分颗粒属于密集流形态，颗粒堆积大部分属于碰撞流，只有在容器左侧及右下侧远离推土板的部分为静态流，因此不能简单运用准静态流(库伦被动土压力理论的物理前提条件)来描述推动阻力。文献[6-7]的研究表明，宏观摩擦系数和惯性数的关系十分密切。本研究的惯性数分布比较复杂，且不同推动速度和不同位移下的惯性数分布也存在差异。

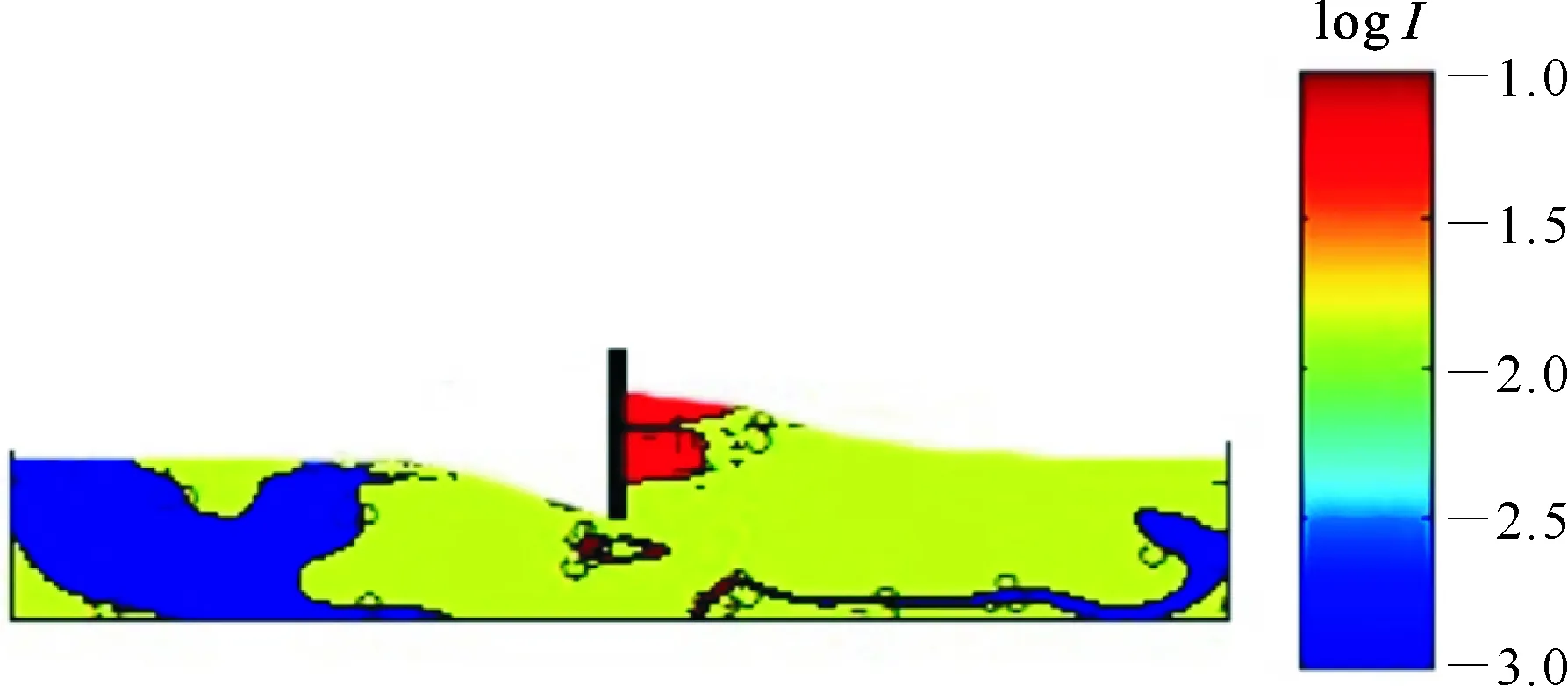
图 6　惯性数(I)在推土板二维颗粒床上的分布(对数值)Fig.6　Distribution of inertial number in 2D granular bed(Logarithm value)

基于此，为了描述非准静态流情况下剪切带上复杂的摩擦特性，本研究定义了一个广义摩擦系数μd，其与推动速度有关，且等于相应的广义摩擦角φd的正切值，可表示为：

μd=tanφd。

(5)

2.4阻力的连续介质模型

由于上部堆积的颗粒是由推土板推动产生的，因此根据几何关系可知位移和侵入深度的乘积等于堆积三角形的面积，这样就可以推导出堆积部分的高度。然而，实际颗粒在堆积的过程中被挤压，密实度增大，因此引入一个高度校正系数，最终颗粒的堆积高度h的计算公式为：

(6)

式中：ζ为堆积高度校正系数，一般取值小于1，这是因为颗粒在推土板推动堆积的过程中密实度增加，堆积高度小于由几何关系推导出的高度；L为容器的宽度；x0为推土板的初始位置；β是上部堆积和竖直方向的夹角；θ表示剪切带与水平面的夹角；Z为侵入深度。

楔体的总面积S为：

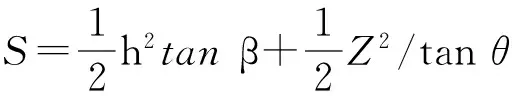
(7)

楔体的受力平衡分析如图7所示，其中G为楔体重力，Np为楔体所受到的法向支持力，μ为剪切带上的摩擦系数，由此得推动阻力Fd的预测公式为：

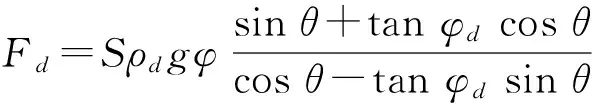
(8)

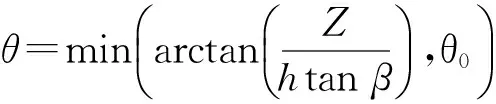
综上可知，本研究求解推动阻力的方法与库伦被动土压力[20]的求法比较类似。不同的是，本研究运用的是改进的适用于非准静态流的广义摩擦系数。

为了探求速度对推动阻力的影响规律，本研究设置了0.2，0.15，0.1，0.05，0.02，0.01和0.005m/s等7个不同的推动速度，以0.2m/s为参考速

度，用函数f(x,V)=bf(x,0.2)表达任意速度下的推动阻力。经过分析发现，b用二次函数拟合效果较好，表达式为：

b=b2V2+b1V+b0。

(9)

式中:V为推动速度；b0、b1和b2为拟合系数，与颗粒材料的物理特性如密度等有关，b2=-5.511 7，b1=4.439 9，b0=0.331 9，R2=0.999。

此时，考虑速度效应的推动阻力表达式为：

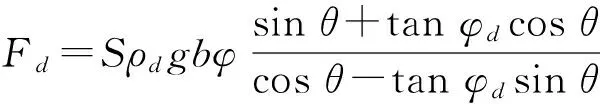
(10)

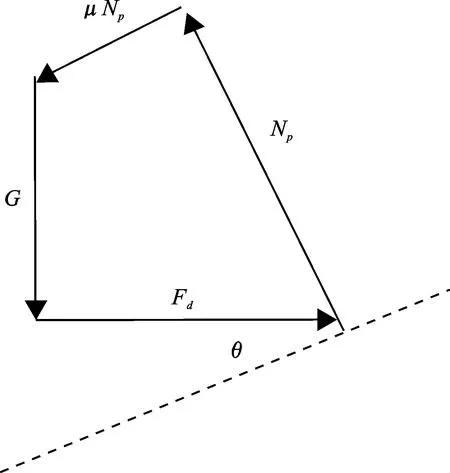
图 7楔体计算模型和受力平衡分析

Fig.7Wedge model and force equilibrium analysis

3　模型验证

用式(10)预测离散元数值试验的结果如图8所示，得到自由参数广义摩擦角φd为38°。用式(10)预测实际物理试验的阻力，广义摩擦角仍然采用数值试验时的38°，并与室内物理试验的结果进行对比，仅以Z=3 cm,V=1 cm/s为例(其他情况结论相似)进行说明，结果见图9。

图 8　推土板颗粒流行为基于改进库伦土压力 理论预测公式的离散元验证Fig.8　DEM verification of the predicted formula based on modified Coulomb theory图 9　预测模型的试验验证(Z=3 cm,V=1 cm/s)Fig.9　Experimental verification for the prediction model(Z=3 cm and V=1 cm/s)

图9表明，该式的预测能力很好，需要指出的有两点：一是为了与数值模拟的结果进行对比，试验数据均作了等效化处理，即均除以推土板的宽度(W=0.05 m)，因为数值模拟的颗粒是单位长度，故无需做处理；二是由于室内试验的局限性，很难在大位移阶段和边界效应阶段得到数据，但是根据室内试验和基于离散元数值模拟的预测模型的对比结果来看，预测模型非常理想。

由前文可知，物理试验中的密实度(三维)与离散元模拟中的密实度(二维)保持一致，颗粒的不均匀率与离散元模拟也保持一致，唯一不同的是物理试验中的颗粒半径较小，为离散元颗粒半径的一半，但是这并未影响二者的高度吻合性。离散元模拟结果已经证实，颗粒半径对推动阻力几乎没有影响，据此认为适当增大离散元模拟的半径，完全可以在不影响结果的情况下提高计算效率。这再一次证明了离散元数值模拟在颗粒流科学分析中的巨大作用，其不但弥补了室内试验的局限性，而且大大提高了计算和分析效率，同时也节约了科学研究的成本。

4　结　论

本研究以竖直光滑推土板为研究对象，对其推动引起的土壤颗粒流行为进行了研究，主要讨论了推动速度对推土板所受阻力的影响，得出如下结论：

(1)提出了基于惯性数理念的土壤在非准静态流情况下广义摩擦系数的概念。

(2)在改进库伦被动土压力理论的基础上，推导出了以推动速度和侵入深度为变量的预测推土板阻力的公式。

(3)通过离散元数值试验和室内物理试验对所得到的预测公式进行了验证，结果表明本研究所建立的推土板阻力预测公式精度较好。

[1]Pouliquen O,Fortrre Y,Ledizes S.Dense granular flows down incline as a self-activated process [J].Advances in Complex Systems,2001,4:441-450.

[2]Silbert L E,Grest G S,Plimpton S J,et al.Boundary effects and self-organization in dense granular flows [J].Physics of Fluids,2002,14(8):2637-2646.

[3]Jiang Y,Liu M.Energetic instability unjams sand and suspension [J].Physical Review Letters,2004,93(14):148001.

[4]孙其诚，王光谦．颗粒物质力学导论 [M].北京：科学出版社，2009.

Sun Q C,Wang G Q.Intruduction to the mechanics of granular materials [M].Beijing:Science Press,2009.

[5]Geng J,Behringer R P.Slow drag in two-dimensional granular media [J].Physical Review E,2005,71(1):011302.

[6]Jop P,Forterre Y,Pouliquen O.A constitutive law for dense granular flows [J].Nature,2006,441(7094):727-730.

[7]Pouliquen O,Cassar C,Jop P,et al.Flow of dense granular material:towards simple constitutive laws [J].Journal of Statistical Mechanics:Theory and Experiment,2006(7):P07020.

[8]张锐，李建桥，周长海，等．推土板表面形态对土壤动态行为影响的离散元模拟 [J].农业工程学报，2007，23(9)：13-19．

Zhang R,Li J Q,Zhou C H,et al.Simulation of dynamic behavior of soil ahead of the bulldozing plates with different surface configurations by discrete element method [J].Transactions of the Chinese Society of Agricultural Engineering,2007,23(9):13-19.

[9]Nott P R.Classical and cosserat plasticity and viscoplasticity models for slow granular flow [J].Acta Mechanica,2009,205(1/2/3/4):151-160.

[10]Rycroft C H,Kamrin K,Bazant M Z.Assessing continuum postulates in simulations of granular flow [J].Journal of the Mechanics and Physics of Solids,2009,57(5):828-839.

[11]Gravish N,Umbanhowar P B,Goldman D I.Force and flow transition in plowed granular media [J].Physical Review Letters,2010,105(12):128301.

[12]Ding Y,Gravish N,Goldman D I.Drag induced lift in granular media [J].Physical Review Letters,2011,106(2):028001.

[13]Percier B,Manneville S,McElwaine J N,et al.Lift and drag forces on an inclined plow moving over a granular surface [J].Physical Review E,2011,84(5):051302.

[14]Hewitt I J,Balmforth N J,McElwaine J N.Granular and fluid washboards [J].Journal of Fluid Mechanics,2012,692:446-463.

[15]Potiguar F Q,Ding Y.Lift and drag in intruders moving thro-ugh hydrostatic granular media at high speeds [J].Physical Review E,2013,88(1):012204.

[16]Kamrin K,Bazant M Z.Stochastic flow rule for granular materials [J].Physical Review E,2007,75(4):041301.

[17]Anon.So much more to know [J/OL].Science,2005,309(5731):78-102 [2005-07-01].http://www.sciencemag.org/content/309/5731/78.2.full.DOI:10.1126/science.309.5731.78b.

[18]Pouliquen O,Forterre Y.A non-local rheology for dense granular flows [J].Philosophical Transactions of the Royal Society of London A:Mathematical,Physical and Engineering Sciences,2009,367(1909):5091-5107.

[19]Guo H,Goldsmith J,Delacruz I,et al.Semi-infinite plates dragged through granular beds [J].Journal of Statistical Mechanics:Theory and Experiment,2012(7):P07013.

[20]Terzaghi K,Peck R B,Mesri G.Soil mechanics in engineering practice [M].New York:John Wiley & Sons,1996.

A continuum model for effect of cohesionless particles on resistant force of vertical bulldozing plate

GUO Hong1,2,LUO Yasheng2,CHEN Xi1,CHENG Dawei3

(1SchoolofCivilEngineeringandArchitecture,ShaanxiSci-TechUniversity,Hanzhong,Shaanxi723001,China;2InstituteofWaterResourcesandHydropowerResearch,NorthwestA&FUniversity,Yangling,Shaanxi712100,China;3SchoolofEnvironmentalScienceandEngineering,Chang’anUniversity,Xi’an,Shaanxi710064,China)

【Objective】 Based on the modified Coulomb passive earth pressure theory,this study investigated the resistant force on the vertical bulldozing plate moving in cohesionless discrete particles at different velocities and immersion depths.【Method】 The indoor physical experiments were conducted based on the modified intruder with two wings to prevent particles from flowing around.Resistant force under different immersion depths(2 cm,3 cm,4 cm)and velocities (1 cm/s and 0.5 cm/s) was then analyzed.A discrete element model was also built to the change of shear band in the particles induced by the bulldozing plate.【Result】 The indoor experiments showed that the calculated displacements under three different immersion depths were 0.15 m,0.11 m and 0.08 m,the drag force increments were 3.4 N,2.5 N and 4.1 N,and the growth rates were 22.7 N/m,22.7 N/m and 51.3 N/m,respectively.Under the same situation,the impact of speed on the drag resistance was not significant.The numerical experiments showed that the shear band was changing with displacement of the bulldozing plate with a clear typical inclined angle.【Conclusion】 Based on shear band and inertial number distribution,a mathematical model for resistant force was established,which well predicted the resistant force.

bulldozing plate;cohesionless discrete particles;granular flow;resistant force;improved Coulomb model

时间:2016-09-0709:03DOI：10.13207/j.cnki.jnwafu.2016.10.032

2015-03-09

国家自然科学基金项目(51178392)；陕西省教育厅专项科研计划项目(15JK1117)；陕西理工学院2015年大学生创新创业训练计划项目(UIRP15087)

郭鸿(1984-)，男，陕西长武人，讲师，博士，主要从事颗粒离散元及岩土力学研究。E-mail：behigh@foxmail.com

骆亚生(1967-)，男，陕西泾阳人，教授，博士生导师，主要从事黄土力学与工程研究。

E-mail：lyas1967@nwsuaf.edu.cn

TU442

A

1671-9387(2016)10-0229-06

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20160907.0903.064.html