基于时差频差角度的低轨双星动目标融合跟踪方法

向张俊，郭福成，张　敏，刘　洋

(国防科学技术大学电子科学与工程学院，湖南 长沙 410073)



·工程应用·

基于时差频差角度的低轨双星动目标融合跟踪方法

向张俊，郭福成，张敏，刘洋

(国防科学技术大学电子科学与工程学院，湖南 长沙 410073)

针对低轨双星时差频差定位系统在对运动目标定位中忽略其运动速度会引起较大的定位偏差以及定位跟踪的初值选取等问题，提出了一种对运动目标的双星时差频差信息融合主星的二维到达角(AOA)信息的融合无源跟踪新方法。首先建立测量模型和等高程目标运动状态模型，在此基础上采用扩展卡尔曼滤波(EKF)方法对运动目标进行跟踪定位。仿真分析表明，该方法可达到克拉美-罗下限(CRLB)，且收敛后对目标的速度和航向估计有较大的提高。

低轨双星；时差频差；测向；定位跟踪

0　引言

双星定位技术通过测量地面静止辐射源的信号到达两颗低轨卫星的时间差TDOA以及两颗卫星相对于目标的运动而引起的到达频率差FDOA[1-3]，可对该辐射源的位置进行精确的定位。由于其相对于三星定位系统少一颗卫星，且比单星定位系统定位精度高等特性，因此在航天电子侦察、监视、搜救等领域具有较好的应用前景。

但对于搭载在具有一定速度的运动平台上(如战斗机、预警机等)的运动辐射源来说，单个时刻的双星时差频差两个观测量理论上无法实现对辐射源位置和速度等参数的瞬时估计。文献[4]指出当地面辐射源处于运动状态时，忽略目标运动速度会给时差频差定位结果造成较大的偏差，所以双星时差频差定位系统如果将运动辐射源当作静止辐射源对其位置进行瞬时估计是不可靠的。在不增加观测卫星数量的情况下对运动辐射源进行定位，一种解决方法是通过多次测量的时差频差对运动辐射源的速度和位置进行跟踪滤波。但由于双星时差频差定位系统是典型的非线性系统，需要采用非线性滤波器技术对目标的位置和速度进行定位跟踪，存在收敛时间长和滤波初值不可靠带来的滤波稳定性问题。文献[5]提出了一种基于UKF的双星时差频差联合定位跟踪算法，以合适的星下点作为迭代初值，但并没有给出初始点的具体方法，所以该方法如果星下点选取不合适，将会导致滤波发散，无法得到正确的位置和速度估计。本文针对双星时差频差定位的滤波初值选取和非线性问题，提出了一种在双星时差频差定位系统的主星上引入DOA信息的基础上，利用EKF技术对地球表面等高程匀速巡航运动目标的融合跟踪方法。仿真分析表明该融合方法的位置估计收敛速度远优于仅用TDOA/FDOA的双星跟踪方法以及单星AOA跟踪方法，对于准确获取运动目标的运动状态信息具有较重要的参考价值。

1　时差频差测向跟踪模型

双星时差频差测向定位系统由一颗主星S1和一颗辅星S2构成，如图1所示，假设主星可以通过二维干涉仪或者阵列测得辐射源到达主星的二维AOA，同时还可联合测得辐射源信号到达两颗卫星的TDOA和FDOA。

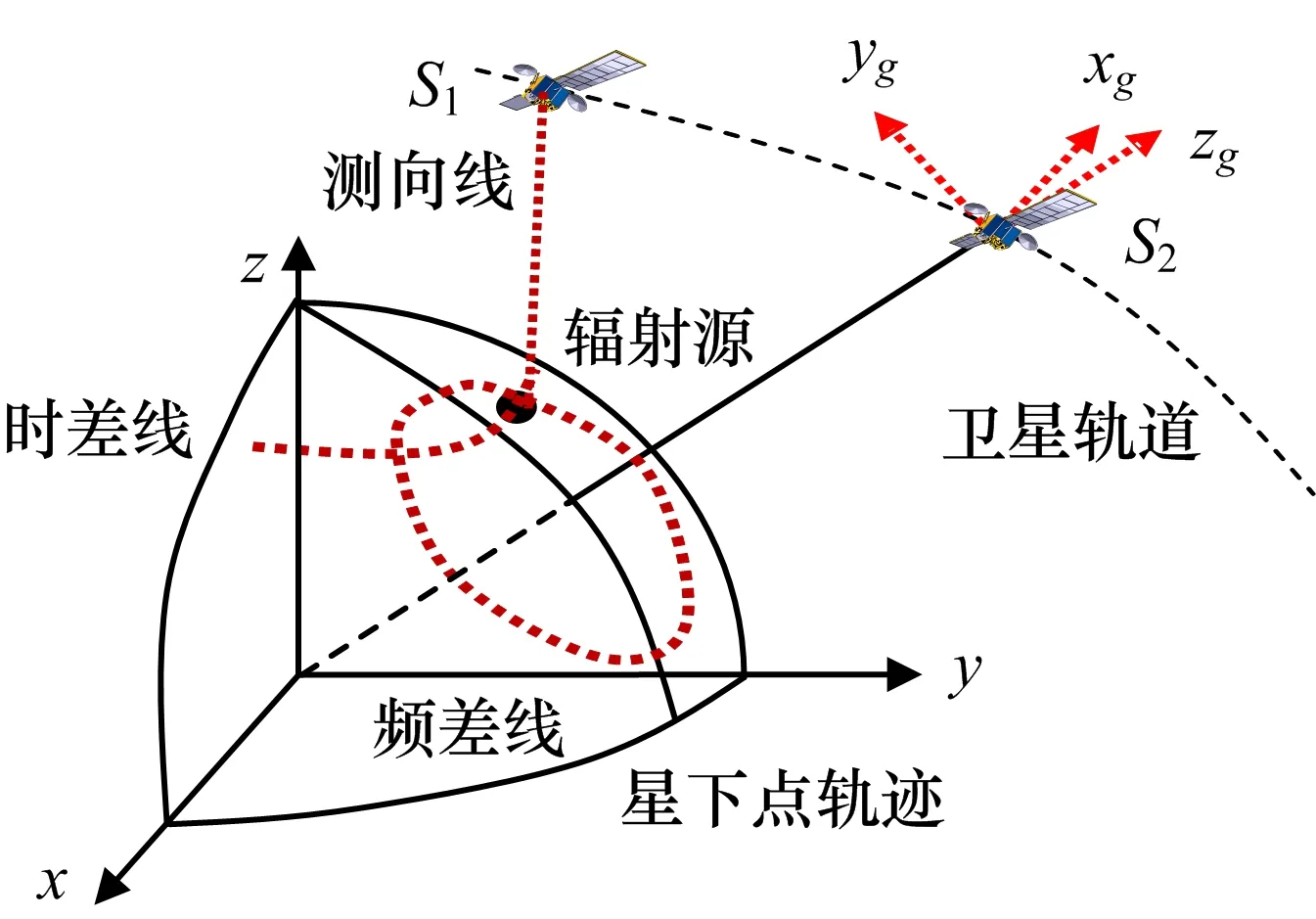
图1　时差频差测向跟踪场景

1.1运动模型

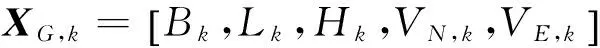
(1)

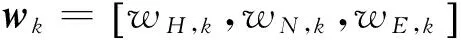
Fk=

(2)

(3)

1.2测量方程

假设k时刻在地心地固(ECEF)坐标系中辐射源目标E的未知坐标为uk，未知速度为vk，主星S1的已知坐标为s1,k，已知速度为v1,k，辅星S2的已知坐标为s2,k，已知速度为v2,k，于是得到式(4)～式(7)。

(4)

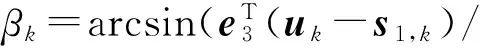
(5)

rk=‖uk-s2,k‖-‖uk-s1,k‖+drk

(6)

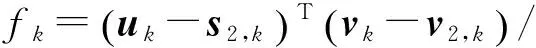
(7)

式中，rk=ctd,k，fk=fd,kc/f0；td,k和fd,k分别表示时差和频差测量量；αk和βk分别表示k时刻主星测得辐射源E相对于主星S1的方位角和俯仰角。为简化讨论，本文假设方位角为测向线与ECEF坐标系的x轴的夹角，俯仰角为测向线与z轴的夹角；dαk，dβk，drk，dfk为相应的测量误差，假设它们为相互独立的高斯白噪声；e1=[1,0,0]T，e2=[0,1,0]T，e3=[0,0,1]T为ECEF坐标系的坐标轴的方向矢量。

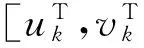
(8)

ECEF坐标系中的位置矢量uk与速度矢量vk和大地坐标系中的状态矢量XG,k存在如下转换关系[7]：

(9)

(10)

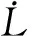
(11)

2　EKF跟踪算法

由于辐射源的测量方程为非线性方程，所以低轨双星时差频差/测向定位系统对辐射源的跟踪，需要采用非线性滤波器技术对辐射源的位置和速度进行多次滤波跟踪。目前，工程上应用较为广泛的非线性滤波器是EKF，它通过对非线性状态及测量函数的泰勒展开式进行一阶线性化截断，将非线性滤波问题转换为线性卡尔曼滤波，是一种次优滤波器[6]，其具有越靠近真实点截断误差越小的特点，所以滤波初值的精确性严重影响EKF滤波器的跟踪性能。本节将介绍跟踪滤波的滤波初值确定方法以及EKF非线性滤波实现。

2.1滤波初值选择方法

考虑到TDOA与AOA的测量量与辐射源的速度无关，所以对辐射源初始时刻位置的估计可以采用AOA融合TDOA得到。根据文献[7]，主星利用测向得到的指向辐射源的方向线与地球球面的交点可以确定辐射源的位置并求得定位误差的协方差矩阵。假设起始时刻辐射源位于高程已知为H的地球表面上空，u0表示辐射源在ECEF坐标系中的位置矢量，于是可以得到：

(12)

将式(12)与式(4)、式(5)联立，目标位置表示为：

(13)

式中，m0=[cosβ0cosα0,cosβ0sinα0,sinβ0]T，r1=‖u0-s1,0‖表示主星到辐射源之间的距离。将式(13)代入式(12)可得关于距离r1的一元二次方程：

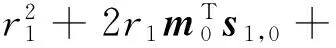
(14)

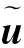
(15)

式中，

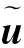
(16)

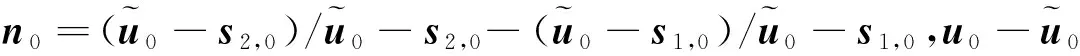
(17)

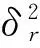
(18)

更新协方差矩阵为：

(19)

(20)

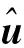
2.2非线性滤波

由于测量方程是关于辐射源的状态向量的非线性函数，EKF算法需要对测量方程在预测状态点处求Jacobian矩阵，下面介绍测量方程的Jacobian矩阵的求法。根据文献[8]和式(11)在预测点XG,k/k-1的Jacobian矩阵为：

(21)

得到初始化数据和测量方程的Jacobian矩阵后，便得可根据如下的EKF公式对辐射源目标进行滤波跟踪[9]。

Step1:利用TDOA融合AOA的方法得到滤波初值XG,0，P0/0；

Step2:预测更新，即：

Step3:坐标转换并计算观测模型的Jcobian矩阵：

H_G, k=∂HE(XE)/∂XE|XE = XE,k/k-1∂XE/∂XG|XG = XG,k/k-1

Step4：测量更新，即：

重复Step2～Step4。

3　仿真分析

通过计算机仿真对提出的算法性能进行分析。假设双星轨道高度为800km，星间距为90km；目标初始位置为(125.801°E，26.3358°N)，目标高程为1000m，运动速度为250m/s,航行为南偏东45°，观测周期为1s，观测时间为120 s，双星定位系统中时差测量误差为30ns,频差测量误差为1Hz，测向误差为0.25°。仿真分析了AOA体制下的EKF算法，采用仅TDOA/FDOA体制下的EKF跟踪方法以及本文的AOA融合TDOA/FDOA体制下的EKF的算法，对运动辐射源进行定位跟踪性能，比较它们的位置估计误差、航速估计误差以及航向角估计误差，并将AOA融合TDOA/FDOA的EKF跟踪方法的位置估计误差和速度估计误差与其CRLB进行了比较，Monte-carlo仿真次数为200次，如图2～4所示。

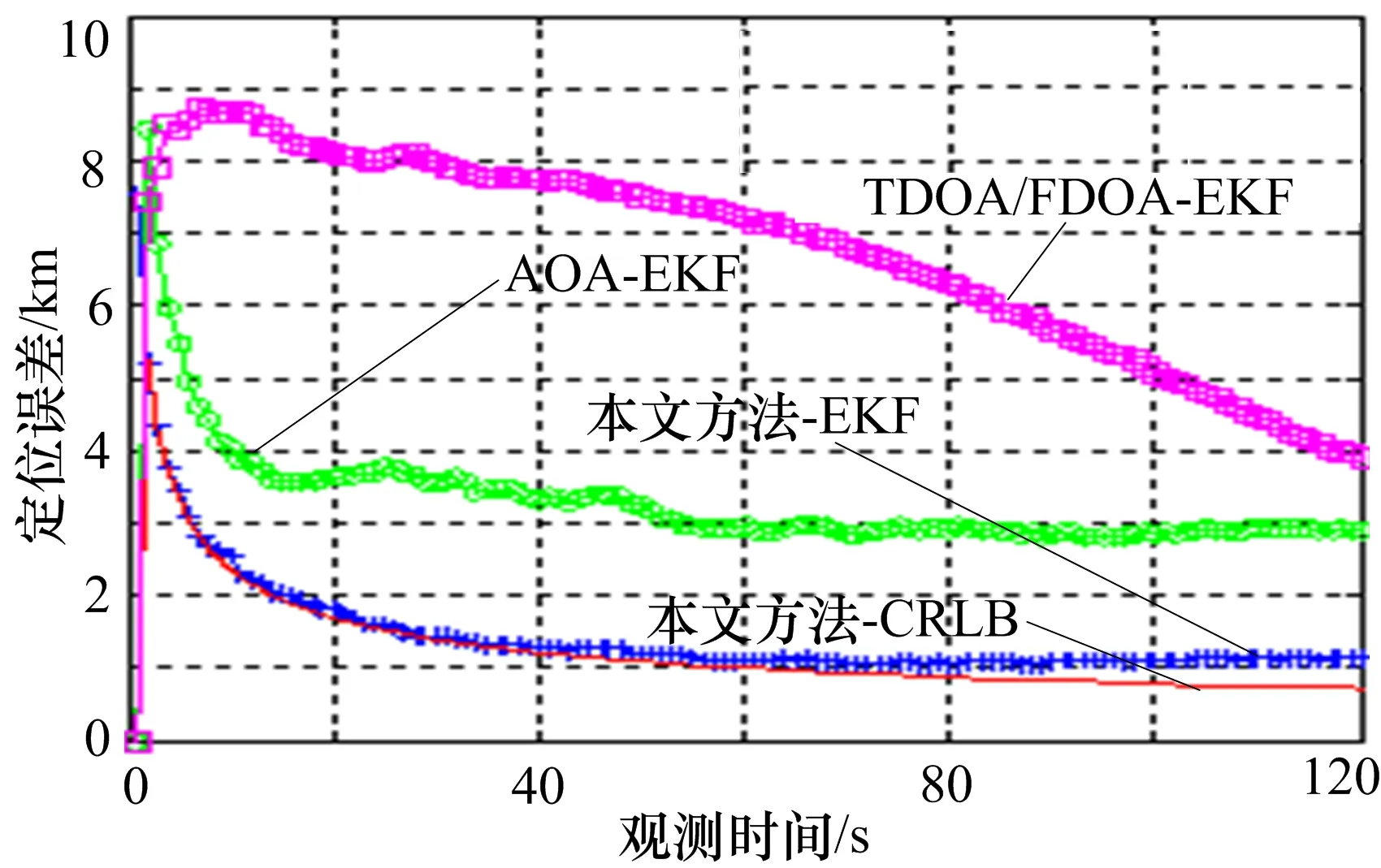
图2　位置估计误差

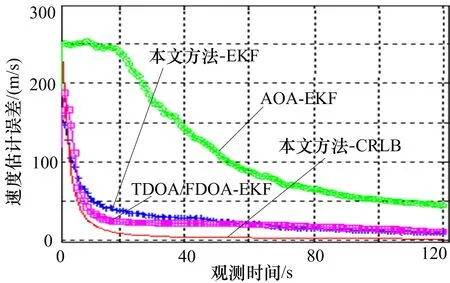
图3　速度估计误差

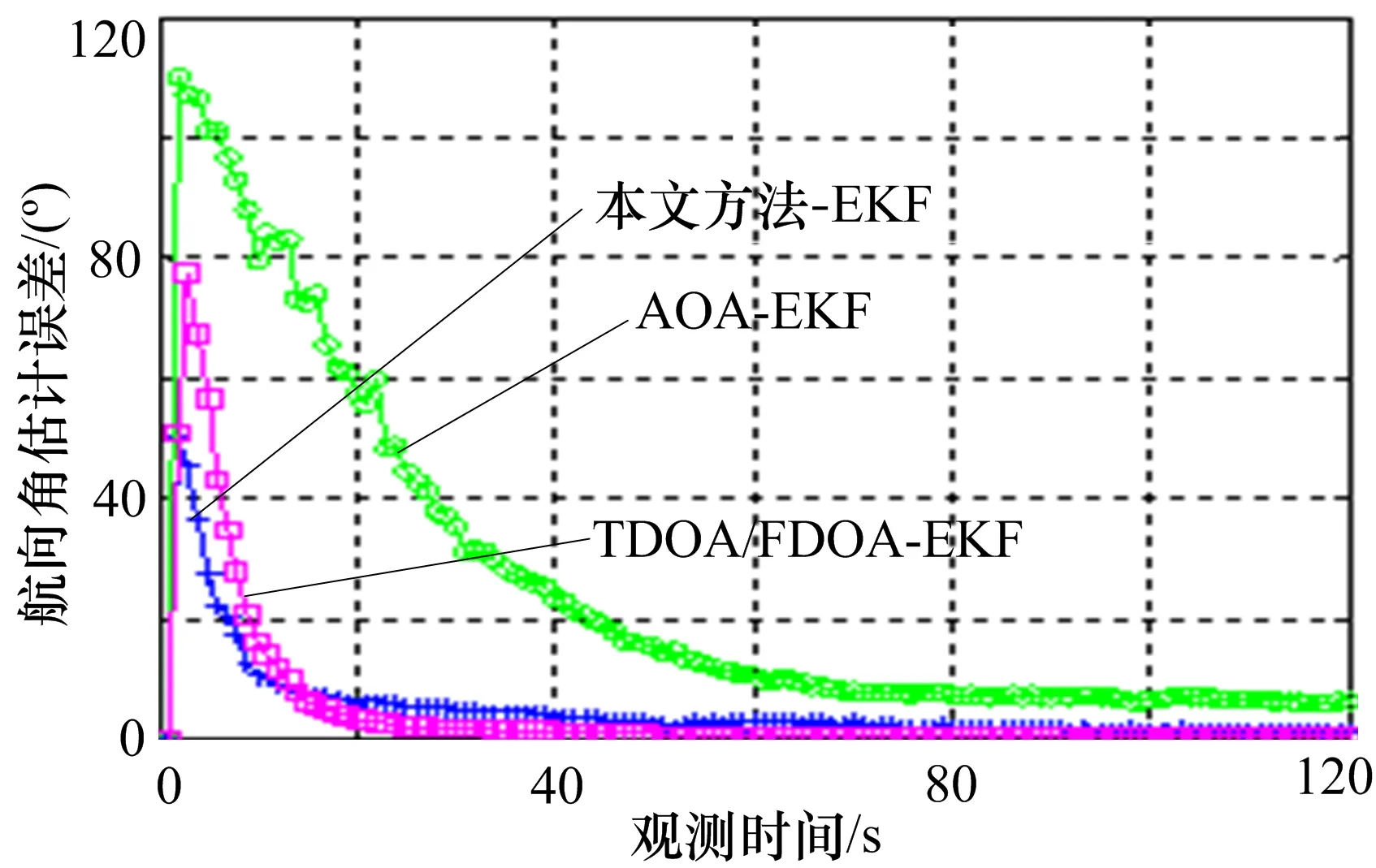
图4　航向角估计误差

从图2可以看出,仅FDOA/TDOA双星跟踪方法位置估计收敛速度缓慢，经过120 s的时间累积仍然无法得到较精确的位置估计(这是由于时差频差测量方程相对于位置参数的强非线性以及初始位置选取不准确而引起的)，而本文所提的TDOA/FDOA融合AOA的双星融合跟踪方法的位置估计相比双星TDOA/FDOA跟踪方法的收敛速度得到大幅提高，同时位置估计精度比单星AOA跟踪方法和双星TDOA/FDOA跟踪方法都有大幅提升且能达到CRLB。从图3和图4可以看出,由于角度测量方程没有速度参数，所以单星AOA跟踪方法的速度跟踪误差较大。而本文所提的TDOA/FDOA融合AOA的融合跟踪方法的速度估计和航向角估计精度比单星AOA跟踪方法高，与双星TDOA/FDOA的跟踪性能相近。这是由于角度信息的引入并没有增加与速度有关的测量量，所以本文方法相比TDOA/FDOA跟踪方法对速度的跟踪性能的改善并不明显。仿真结果充分说明了本文所提融合跟踪方法的优越性。

4　结束语

本文针对低轨双星时差频差定位系统在对运动目标跟踪时存在收敛速度较慢以及跟踪初值确定问题，提出了基于TDOA/FDOA融合AOA的低轨双星融合跟踪方法，首先利用AOA融合TDOA确定辐射源的初始状态和初始协方差矩阵，然后利用EKF进行滤波跟踪，仿真结果表明融合跟踪方法在位置跟踪方面性能远优于单星AOA跟踪方法和双星TDOA/FDOA跟踪方法，且位置跟踪性能可以达到CRLB，在速度和航向角方面的跟踪性能远优于AOA跟踪方法，但与TDOA/FDOA跟踪方法相近。■

[1]Ho KC, Chan YT. Geolocation of a know altitude object from TDOA and FDOA measurements [J]. IEEE Trans. on Aerospace and electronic systems, 1997,33(3):770-783.

[2]郭福成，樊昀.双星TDOA/FDOA无源定位方法分析[J].航天电子对抗，2008，24(6)：20-23.

[3]郭福成，樊昀.双星时差频差联合定位方法及其误差分析[J].宇航学报，2008，29(4)：1381-1386.

[4]Ulman RJ，Geraniotis E．Motion detection using TDOA and FDOA measurements[J]．IEEE Trans. on AES，Science (SOOl8-9251)，2001，37(2)：759-764．

[5]赵侃，漆德宁.基于UKF滤波的FDOA和TDOA联合定位跟踪算法[J]．计算机技术与发展，2012,22(5): 127-129.

[6]赵琳,等.非线性系统滤波理论[M].北京:国防工业出版社，2012.

[7]郭福成，樊昀,周一宇，等.空间电子侦察定位原理[M].北京：国防工业出版社，2012.

[8]罗鹏飞. 统计信号处理[M].北京：电子工业出版社.2009.

[9]何友，王国宏，陆大琻，等．多传感器信息融合及应用[M]．北京：电子工业出版社，2007.

Tracking method of moving target fusion for low orbit dual-satellite based on TDOA/FDOA/AOA

Xiang Zhangjun, Guo Fucheng, Zhang Min, Liu Yang

(College of Electronic Science and Engineering,National University of Defense Technology, Changsha 410073,Hunan,China)

For the problem that TDOA and FDOA based on dual-satellite geolocation system, when the target is moving, the unknown velocity of the target leads to large localization errors and initialization problem of the tracker. The angle of arrival (AOA) measurement is introduced to improve the observability of dual-satellite system and proposes a target tracking method of hybrid TDOA/FDOA/AOA location system. Firstly, the measurement model and elevation target motion state model are established, and then the extended Kalman filter (EKF) is adopted to track the moving target. The simulation results prove that the hybrid TDOA/FDOA and AOA tracking method can achieve cramer-rao lower bound (CRLB) and obviously improve the accuracy of the velocity and location estimation．

low orbit dual-satellite；TDOA/FDOA；direction-finding；target tracking

2016-03-03；2016-04-07修回。

向张俊(1991-)，男，硕士研究生，主要研究方向为无源定位。

TN97

A