巧妙建构模型加深数学理解
潘丽(松溪县实验小学,福建松溪353500)
巧妙建构模型加深数学理解
潘丽
(松溪县实验小学,福建松溪353500)
模型思想是新版数学课程标准提出的10个核心概念中唯一一个以“思想”指称的概念。数学教学中,教师应充分重视渗透模型化思想,利用合适的素材帮助学生建立并把握有关数学模型,发展“模型思想”,促进学生在数学上获得更好的发展。
模型思想;建模
模型思想是《义务教育数学课程标准(2011年版)》新增的核心概念,也是10个核心概念中唯一一个以“思想”指称的概念。数学教学中应当引导学生感悟建模过程,发展“模型思想”,为学生的终身学习,可持续发展奠定基础。
那么,如何发展学生的模型思想呢?
一、选择合适的问题情境是建模的土壤[1]
数学模型的建立要以具体问题为载体,选择的问题情境要典型、有代表性,充分反映学生对学习的主观愿望,能激发学生的学习兴趣,唤起学生对知识的渴望和追求。教师要积极创设有效的利于建模的问题情境。在教学北师大版四年级上册《路程、时间与速度》一课的导入环节时,一位教师进行了如下处理。
1.第一场比赛
师:咱们班有三位同学为“谁跑得快”的问题而争论不休,于是他们三人比了一场,请看比赛结果。

师:你们看到了哪些数学信息?你是怎么想的?
生1:他们都跑了50米。
生2:陈绍纬跑得最快,因为他只用了8秒。
师:如果路程相同,比快慢可以比时间。
2.第二场比赛
师:我也加入了他们的比赛,请看

生3:还是陈绍纬跑得快。
生4:(迫不及待地抢答)虽然你们都是跑了8秒,可是他跑了50米,你才跑了48米。
师:如果用的时间相同,比快慢可以看——
生:(异口同声地)路程。
3.第三场比赛

生5:我发现李老师和张铖比赛,时间和路程都不相同,这怎么比啊?
生6:把他们也变成时间一样或路程相同就行了。如果他们都跑了80秒,该教师跑了48×10=480(米),张铖跑了50×8=400(米),480>400,所以李老师跑得快。
生7:不用那么麻烦,直接比速度。
李老师:48÷8=6(米)
张铖:50÷10=5(米)
师:6米表示什么?5米呢?
生7:表示他们1秒跑多远。
师:根据这位同学列出的算式,你能解读刚才他说的速度的含义吗?
……
以上“谁跑得快”的问题情境的设计是基于学生已有经验的。李老师巧妙地将不同特点的数据蕴涵于情境之中,鼓励学生在开放的数学活动中运用经验从多种角度思考问题的解决方法。不仅让学生真切地体会到跑的快慢时间、路程有关,更使学生感受到了路程、时间都不相同时,速度产生的必要性。问题的选择富有生活气息,符合学生的兴趣爱好和年龄特征,使他们全身心地投入到学习中,自然导入了“速度=路程÷时间”模型的学习。
二、抽象本质属性是建模的关键
《义务教育数学课程标准(2011年版)》指出,学生要通过观察、分析、抽象、概括、选择、判断等数学活动,从具体的表象中抽象出本质特征,完成模式抽象,得到模型。这是建模最重要的一个环节。
在教学人教版数学三年级上册《分数的初步认识》[2]时,为让学生抽象出分数本质,笔者设计了以下三个环节。
环节一:铺垫
师(课件出示盘子里装着一个蛋糕):羊村长要把一个蛋糕平均分给四只小羊,每只羊可以分到多少蛋糕?
生1:个。
师:真好,你是怎么想到这个分数的?
生1:把一个蛋糕平均分成4份,每只小羊分到其中的一份,就是这个蛋糕的。
师(出示课件):哪幅图可以表示刚才分蛋糕的情况?说说你的理由?

环节二:思辨
师(课件出示用布遮住的第二盘蛋糕):看着这盘蛋糕,你们猜羊村长会怎么分呢?
生2:也是平均分成4份,这样最公平。
师:这个盘子到底有几个蛋糕呢?(出示8个蛋糕的集合图)你能帮村长分一分吗?(生比划着分。)
师:每只小羊分到这些蛋糕4份中的一份,也就是这些蛋糕的……
生3:。
师:这次分蛋糕的情况还能用刚才这两幅图表示吗?(出示课件)

生1:我认为不能,这里有8个蛋糕,刚才只有1个蛋糕。
生2:我认为能,这个大长方形表示的是8个蛋糕,把它平均分成四份,每只小羊分到的是其中的一份。
生3:我也认为能。第一次分,大长方形表示一个蛋糕,第二次分,大长方形表示的是8个蛋糕组成一个整体。
师:整体这个词用得妙!刚才两次分的过程,无论是一个蛋糕,还是8个蛋糕,只要是把它平均分成4份,其中的1份都是整体的。
环节三:提升
(学生画图,展示交流。)
生4:不用这么麻烦,用刚才的图也能表示12个蛋糕的。
师:这两幅图有这么厉害?
生4:是的,大长方形12个蛋糕,把它平均分成4份,其中的1份就是整体的。
生5:16、20、24、40……
师:原来整个图代表一个整体,不论整体里有几个蛋糕,只要是把它平均分成4份,其中的1份就是它的。
教师引领学生经历了“猜测—想象—操作”的过程,学生在不同观点的碰撞、讨论、辨析中,沟通了“一个物体的几分之一”与“一些物体的几分之一”的联系,强化了“整体”意识。剥离掉物体个数等非本质属性,抽象出分数的本质属性,建立了几分之一的直观模型,实现了建模质的飞跃。
三、浸润数学思想是建模的灵魂
数学思想是数学教学的精髓,在建模过程中,教师要重视数学思想方法的渗透,让学生在“润物细无声”中体验和感悟数学思想方法,增加建模的思维厚度。教学人教版二年级上册第八单元“数学广角”第一课时《简单的排列组合》[3],笔者引导学生运用分类方法进行有效推理。
师:懒羊羊到商店买蛋糕,它挑中了一个香草味的蛋糕,标价是5元。懒羊羊手里有1张5元的纸币、2张2元的纸币、5个1元硬币。请同学们帮懒羊羊想一想,可以怎样付钱?最多有几种付钱方案?
(学生交流讨论。)
师:指名汇报并将学生的付钱方案填入表格中。

师:找全了吗?
(学生面露难色不敢肯定。)
师:这样吧,我们按照每次用的人民币的种类和张数排列一下,你们再来观察一下。
(师生一起整理:按顺序,依次只付5元、2元和1元的……)
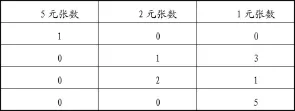
师:现在找全了吗?
生齐:找全了!
师:为什么这次一下就知道没有重复和遗漏呢?
生1:因为我们是按照顺序将所有可能性一一列举的。
以上教学注重数学思想方法的渗透,教师先使学生感受到无序的杂乱,然后巧妙地将无序转化成有序,使学生感受到有序的好处。从无序到有序,学生不仅解决了问题,同时还感受到有序思想的重要性,学生的思维逐渐走向深入。
四、解决一类问题是建模的拓展
用新建立的数学模型来解释生活现象,解决生活实际中的问题。让学生体会到数学模型的应用价值,体验到所学知识的用途和益处,以此深化模型的内涵,拓展模型的外延。
如:郑玲玲《抽屉原理》教学片段[4]
师:刚才我们借助抽屉和小球研究了这个原理,有的国家是用鸽子和鸽笼研究的:7只鸽子飞进5个鸽笼,至少有几只鸽子要飞进同一个鸽笼?
生1:7÷5=1……2,1+1=2,至少飞进2只鸽子。
师:这里的鸽子相当于什么?鸽笼呢?
生1:这里的鸽子相当于物体,鸽笼相当于抽屉。
师:抽屉原理也被人们形象的称为鸽笼原理。把鸽笼看作抽屉可以叫鸽笼原理,如果把文具盒看作抽屉,可不可以叫文具盒原理?假如有4个文具盒,5支铅笔,总有一个文具盒里有几支铅笔?
生2:不管怎么放,总有一个文具盒里有2支铅笔。
师:有口袋吗?6枚硬币,4个口袋,不管怎么放,总有一个口袋里有几枚硬币?
生3:不管怎么放,总有一个口袋里有2枚硬币。
师:口袋原理又诞生了,好玩吗?要按这种叫法,抽屉原理还可以有很多名字。看来,抽屉原理在生活中随处可见,它其实就是解决该类问题的一种方法,一个模型。在解决问题时关键要看清什么是抽屉,什么是要分的物体。现在你能用抽屉原理来解释为什么课前老师说30位同学中至少有8人在同一个季节里过生日吗?
生4:把30位同学看作待分的物体,四个季节看作抽屉,30÷4=7……2,7+1=8,30位同学中至少有8人在同一个季节里过生日。
师:你能再来解释30位同学中至少有3人在同一个月里过生日吗?
(学生解释。)
师:我国宋代的学者费衮在《梁溪漫志》一书中就曾运用抽屉原理来批驳过算命。直到十九世纪德国的狄利克雷才把它抽象成抽屉原理。
数学模型来源于生活,还要应用到生活中。教师利用抽屉原理模型解释鸽笼原理、文具盒原理、口袋原理、生日问题等生活中的问题,让模型更加丰满具有生命力,同时,培养了学生分析问题、解决问题的能力,渗透了模型思想。
总之,在小学数学教学中,应充分重视渗透模型化思想,利用合适的素材帮助学生建立并把握有关数学模型。教师要充分认识到模型思想在整个数学学习过程中的价值,通过建模教学,逐步培养学生数学建模的思想方法,促进学生在数学上获得更好的发展。
[1]杨豫晖.义务教育课程标准(2011年版)案例式解读小学数学[M].北京:教育科学出版社,2012.
[2]曹小培.借几何直观建分数模型促深透理解[J].教学月刊,2013(7-8).
[3]吴正宪.小学数学课堂教学策略——师生互动共同创建有效课堂[M].北京:北京师范大学出版社,2012.
[4]王吉鹏.思想感悟让数学模型更加丰满[J].小学教学设计,2014(4).
(责任编辑:陈志华)
本文系2014年度福建省基础教育课程教学研究立项课题“小学数学教学设计理论与实践研究”(项目编号:MJYKT2014-232)阶段性研究成果。

