“相等”来搭桥 天堑变通途——谈不等式等号成立条件的简单应用

黄旭东

(湖北省黄石市第一中学，435000)



“相等”来搭桥天堑变通途
——谈不等式等号成立条件的简单应用

黄旭东

(湖北省黄石市第一中学，435000)

在中学阶段,常常利用一些基本不等式或一些重要不等式进行证明或求最值,其应用相当广泛．而在实际运用过程中,一些同学常常忽视了不等式等号成立的条件,进而造成了一些错误,甚至造成一些题目无法获解．实际上,基本不等式与重要不等式等号成立的条件应用相当广泛,甚至在一些较难题目中,灵活运用“相等”来搭桥,天堑也会变通途!

一、证明不等式

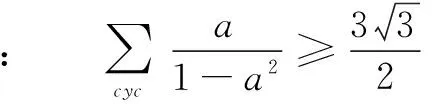
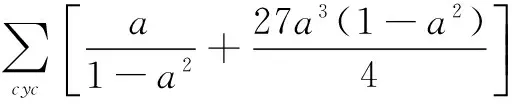
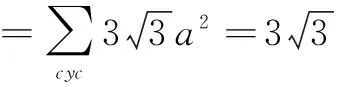
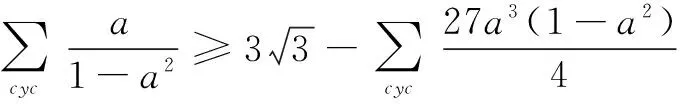
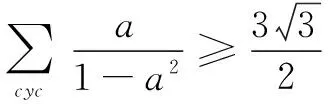
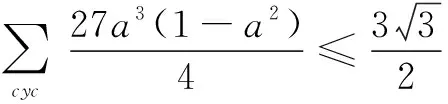
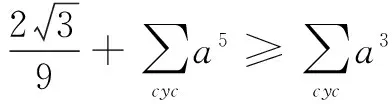
由a2+b2+c2=1，得

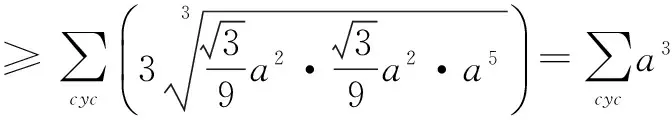
故原不等式成立.

评注对于一些轮换条件不等式,等号成立当且仅当各参数值相等;对一些非轮换条件不等式，有时可考虑用比例法取等号，再结合均值不等式等号成立条件配相应因子,从而使问题向所证目标顺利转化．

二、巧解方程与不定方程

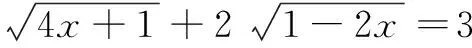
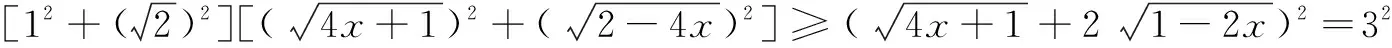
例3求方程3(ab+bc+ac)=2abc的所有正整数解.

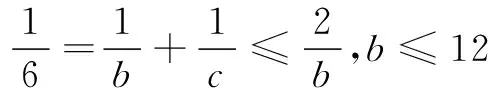
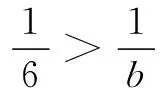
7≤b≤12,b∈N*.

又由c∈N*,可得

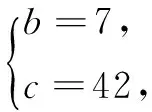
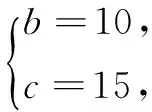
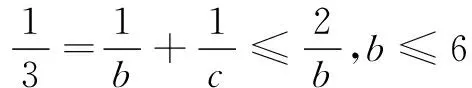
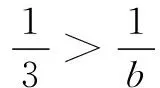
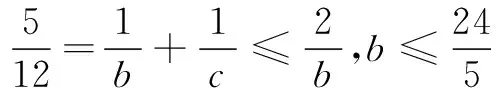
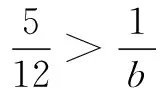
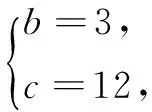
由(1)(2)(3)知,满足条件的解集为{(2,7,42),(2,8,24),(2,9,18),(2,10,15),(2,12,12),(3,4,12),(3,5,15),(3,6,6),(4,3,12),(4,4,6)}.

评注一些表面很繁杂的方程有时暗含某些基本不等式或一些重要不等式等号成立的条件,若能有效观察出,问题将轻易获解.例2便是暗含柯西不等式等号成立条件;而有些复杂的不定方程,有时通过不等式等号成立条件使变量放缩,缩小变量范围,再逐步讨论解出.

三、巧求多变量参数

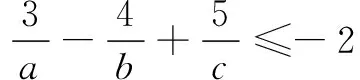
解4a2-2ab+4b2-c

=(2a+b)2-6ab+3b2-c

=(2a+b)2-3b(2a-b)-c

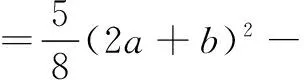
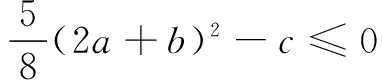
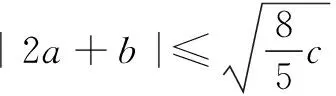
等号成立条件为2b=2a-b，即3b=2a.

此时c=(3b)2-3b·b+4b2=10b2,

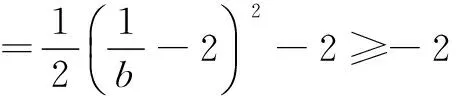
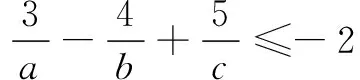
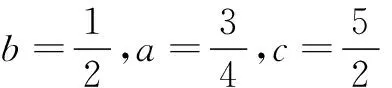
评注一些多变量不等式中求其值,往往考虑不等式等号成立条件或两边夹思想．

四、在三角中的应用

例5函数y=7sin x-24cos x取最小值时，sin x=______.

解y2=(7sin x-24cos x)2≤[72+(-24)2](sin2x+cos2x)=625,则有

|y|≤25,ymin=-25,

等号成立条件为

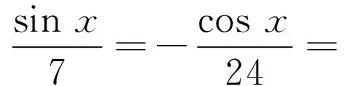
故有-25=7×7k-24(-24k)=625k，

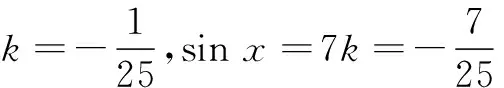
例6已知∆ABC中,AC=8,AB=c,且S∆ABC=4+c2,求∆ABC内切圆半径.

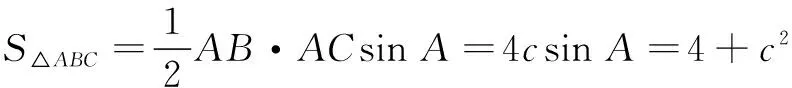
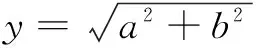
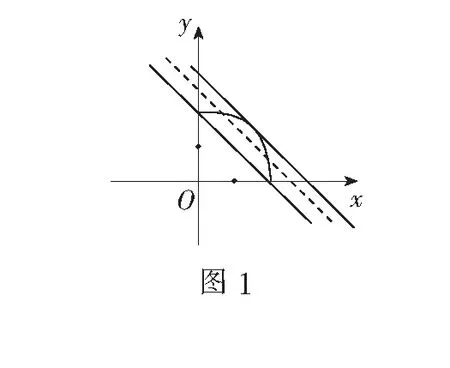
五、在几何中的应用

解由

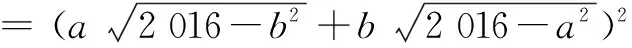
=2 0162，

知不等式等号成立,故有

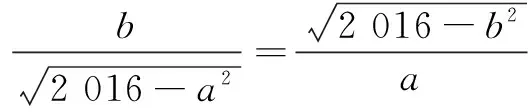
得a2+b2=2 016(a≥0,b≥0).

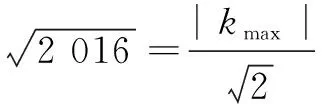
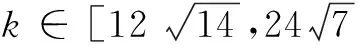
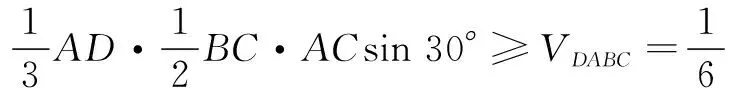
①

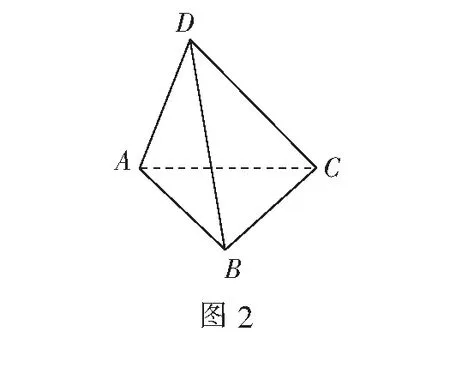
又3=AD+BC+AC

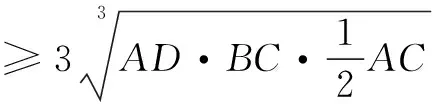
故有AD·BC·AC≤2.

②

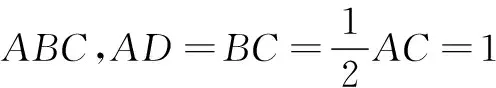
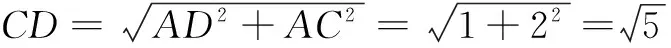
评注不等式等号成立条件在几何中的应用充分体现了数学世界中“动静”互变,“不等”中含“等”的独特魅力!同时也充分验证了代数与几何是两个孪生兄弟的格言!

可以看出，上面的f(x)满足的条件中x的系数一个为1，另一个为-1时,函数f(x)存在对称中心.