阈值判决引导的单载波分块传输稀疏信道估计

孟庆微，苏令华，苏玉泽，孟相如，黄仰超

(空军工程大学 信息与导航学院，陕西 西安 710077)



阈值判决引导的单载波分块传输稀疏信道估计

孟庆微，苏令华，苏玉泽，孟相如*，黄仰超

(空军工程大学 信息与导航学院，陕西 西安 710077)

为利用高速无线通信时信道的稀疏多径传播特性，改善传统单载波分块传输(SCBT)信道估计方法的性能，提出了一种阈值判决引导的稀疏信道估计方法。该方法通过导频进行初始最小二乘信道估计，利用获取的信道估计值设置判决阈值。然后，将幅值低于判决阈值的信道抽头强制置零，仅保留幅度值大于判决阈值的信道抽头估计值，从而有效地改善单载波分块传输系统的稀疏信道估计性能。基于COST 207典型乡村信道模型进行了仿真实验，结果表明：阈值判决引导的稀疏信道估计方法的实验结果最接近于信道参数已知时的误比特率性能；在信噪比为20 dB条件下，新方法的误比特率可达到5×10-4，而最小二乘算法只能达到3×10-2。该方法改善了SCBT系统的稀疏信道估计精度与复杂度，得到的结果验证了提出方法的有效性。

无线通信；单载波分块传输；阈值判决；稀疏信道估计

1　引　言

近年来，数字通信系统的语音、视频和数据业务需求不断增长，无线通信传输速率显著提高，信道多径传播造成的码间串扰(ISI)越来越严重，达到几十甚至上百个码元间隔，

传统单载波连续传输方法逐个符号进行时域均衡，导致接收机复杂度大幅度提高。分块传输技术可利用快速傅里叶变换(FFT)计算频域均衡器的抽头系数，大幅度降低了接收机的复杂度，其中，单载波分块传输(Single Carrier Block Transmission， SCBT)方案可以解决正交频分复用(Orthogonal Frequency Division Multiplexing， OFDM)系统峰均比高且对频率偏移敏感的问题，但系统性能和复杂度与之相当，已成为后3G(Beyond 3G)无线通信系统的关键技术之一，目前已被3GPP LTE计划和IEEE 802.16标准确定为上行链路传输标准，并广泛应用于水声通信[1]、数字广播电视、航空通信[2]以及超宽带通信[3]等场景。

可靠的信道估计是高速数字通信调制解调的核心环节。常用的信道估计方法主要包括两类：导频辅助信道估计方法和盲信道估计方法。盲信道估计方法计算复杂度高、收敛速度慢，因此绝大多数无线通信系统通常以消耗少量频率带宽为代价，在发射数据帧中插入导频信号，以便接收端可以简单、可靠、实时地完成信道估计。SCBT系统的导频辅助信道估计方法主要包括基于最小二乘准则的信道估计方法[4-5]和PN序列相关信道估计[6-7]方法。PN序列相关信道估计方法计算复杂度低，实现简单，但性能较差。最小二乘信道估计方法广泛应用于高速无线通信系统，其在多径密集型分布的无线信道中性能最优。

随着无线通信传输速率的不断提高，信道稀疏多径传播特性越来越显著，其传输能量通常集中在少数几条路径上。信道的稀疏多径传输特性为高速无线通信提供了机遇，同时也带来了挑战。机遇在于稀疏信道比多径密集型分布的无线信道具有更大的信道容量[8]，而挑战则在于传统估计方法在稀疏信道应用时，忽略了信道的稀疏多径传播特性，信道估计精度差，不但浪费了宝贵的传输能量和系统带宽，还会造成系统误码率严重[9-14]。

利用信道的稀疏多径传播特性，提高高速无线通信系统的信道估计精度是无线通信的研究热点。目前，基于压缩感知的稀疏信道估计主要针对OFDM系统，根据信道特征和OFDM系统模型，构造测量矩阵[9-11]，优化重构算法重建信道响应值[12]。SCBT和OFDM系统之间存在相似性，但两者在组帧方式、导频插入方法之间差异十分明显。因此，OFDM系统的压缩感知测量矩阵构造方法无法直接应用于SCBT系统。文献[13]证明任意单位能量导频，经过适当的变换后均可用于构造压缩感知测量矩阵，并用于稀疏信道估计。文献[14]中证明PN序列是构造压缩感知测量矩阵的最佳序列。上述文献仅研究了测量矩阵的构造问题，重构算法仍然利用经典的凸优化算法，计算复杂度高。因此，本文将提出一种基于阈值判决的低复杂度单载波分块传输稀疏信道估计方法，以有效解决SCBT系统的信道估计精度与复杂度问题。

2　系统模型

本文主要研究循环前缀单载波分块传输(CP-SCBT)系统，其与传统单载波连续传输系统之间的一个显著差异在于数据组帧方式不同，CP-SCBT主要采用分块形式进行组帧，每个传输数据帧包含一定数量的数据分块和导频分块，每个导频分块与数据分块间插入循环前缀(CP)作为保护间隔，防止块间串扰(IBI)。同时，循环前缀分块结构还可以将发射信号与信道的线性卷积转换为循环卷积，以便接收机利用FFT/IFFT进行低复杂度频域处理。CP-SCBT系统框图如图1 所示，数据帧结构如图2所示，其中，导频分块用于信道估计，数据分块用于数据传输。

图1　SCBT系统组成框图

图2　SCBT传输系统的数据帧结构

在发射端，需要发送的二进制数据0、1经过分组，符号调制之后，添加循环前缀(CP)组成时域符号块，多个数据块组成如图2所示的数据帧，经无线信道传输至接收端。

由于高速无线传输中信道多径传输存在显著的分簇扩展传播特性，信道能量通常集中在少数路径上。假定频率选择稀疏信道的长度为L，其信道冲激响应可表示：

(1)

其中：hl为第l个路径的信道增益。本文考虑信道慢变的情形，即信道冲激响应h=[h0，h1，…，hL-1]T在整个数据帧内基本保持不变，信道全部L个抽头中仅有S个抽头取值较大，其余信道抽头幅值接近于零，即：

‖h‖l0=S，S≪L.

(2)

假设CP-SCBT系统的CP长度大于稀疏信道冲激响应长度L，那么各传输分块之间将不存在分块间干扰(IBI)。接收机在完成帧同步和符号同步后，丢弃每个分块的CP部分，仅保留剩余的N维接收信号向量y=[y0，y1，…，yN-1]T，可表示为：

y=Hx+n，

(3)

其中：x=[x0，x1，…，xN-1]T为发射机端发送的调制信号，n=[n0，n1，…，nN-1]T是方差为σ2的独立同分布高斯白噪声向量。H为信道矩阵，可表示为：

(4)

其中hl为第l条路径的信道增益。

在接收端，接收机对时域接收信号向量y=[y0，y1，…，yN-1]T进行归一化FFT变换，将时域信号转换到频域，即：

Y=Fy=FHx+Fn.

(5)

其中：Y=Fy为时域接收信号进行归一化傅里叶变换后获得的频域信号：

其中1≤m，n≤N为归一化N点傅里叶变换矩阵。

由于式(4)中H为循环矩阵，可得：

H=FHGF，

(6)

其中：

G=diag(g)，

g=[g0，g1，…，gN-1]T，

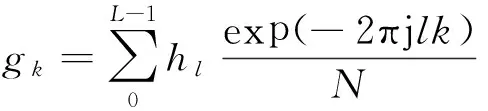
(7)

式中：diag(·)表示对角阵，gk为第k个频点处的信道频率冲激响应值。

将式(7)代入式(6)，接收信号的频域变换形式可表示为：

Y=Fy=FFHGFx+Fn=GFx+Fn.

(8)

然后，将式(8)中的频域信号进行频域均衡，单抽头频域均衡器的系数可由式(9)计算获得：

W=(GGH+σ2I)-1G.

(9)

接收机利用频域均衡器补偿信道造成的码间串扰(ISI)，可表示为：

Z=WHY.

(10)

再将频域均衡结果进行IFFT变换，转换回时域，即：

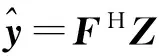
(11)

3　基于阈值判决的低复杂度稀疏信道估计方法

3.1最小二乘信道估计

在CP-SCBT系统中，可利用导频块进行信道估计，数据块内信道估计值可保持不变或者利用内插方式获取[5]。接收的导频块信号可写为：

y=p⊗h+n，

(12)

(13)

并简记为：

y=Ph+n，

(14)

其中：P是导频向量构成的矩阵，由于信道冲激响应的长度在接收机端难以先验获取，通常假定式(13)中的信道冲激响应长度与导频块长度相同，最小二乘信道估计值可按照下式获取：

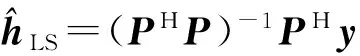
(15)

式(15)中，接收机只需要先验获取导频矩阵P的信息即可，计算简单，实现方便。笔者曾在前期研究中证明了PN序列在CP-SCBT系统稀疏信道估计中作为导频具有最优性[14]，本文仍沿用上述结论构造导频矩阵P。

但是，式(15)所示的最小二乘信道估计方法在稀疏信道应用中，由于其对所有信道抽头采用相同权重，而稀疏信道传输能量主要集中在少数路径中，绝大多数路径幅值较小，从而会造成信道取值较小部分幅值出现“过估计”。凸优化算法[13-14]能够抑制较小信道抽头值，但计算复杂度过高，实际应用受限。故本文提出一种基于阈值判决的低复杂度信道估计方法，用于改善稀疏信道估计精度。

3.2阈值设定

因此，在音乐教学中注重对学生节奏感的培养，一方面可以为学生后续深入性的音乐学习打下基础；另一方面，也能强化其对音乐的感知能力、判断能力，使其受到音乐的感染、启发，真正的发觉音乐的魅力、价值，使其得以更加综合、全面的发展下去。

为避免具有较小幅值信道抽头“过估计”的影响，可通过设置阈值对传统LS信道估计方法获取的信道抽头进行筛选，仅保留幅度值高于阈值的信道抽头，强制将低于阈值的信道抽头置零。为提高阈值估计的准确度，本文利用“粗估计”、“精估计”两步实现阈值判决过程。

假定无线稀疏信道存在的噪声为加性高斯白噪声，其包络服从瑞利分布，概率密度函数为：

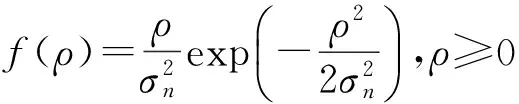
(16)

其分布函数为：

(17)

式中：σn表示噪声向量n中每个分量的标准差，ρ为噪声包络。

服从瑞利分布的随机变量，其中值x满足：

(18)

即：

(19)

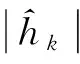
(20)

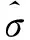
接下来，接收机利用硬判决机制剔除信道中幅度较大的信道抽头，可表示为：

(22)

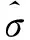
(23)

在精确估计噪声标准差后，按照式(21)重新计算判决门限：

(24)

然后，再利用式(24)计算获取的判决门限值，进行硬判决，可表示为：

(25)

3.3算法流程

本文提出的阈值判决引导单载波分块传输稀疏信道估计方法(TDDSCE)的流程图如图3所示。

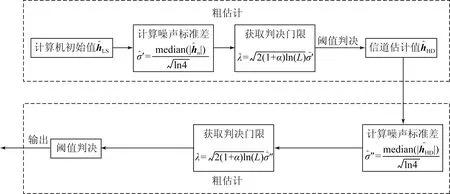
图3　算法流程图

具体流程如下：

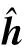
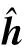
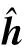
4　计算机仿真

为验证本文提出的TDDSCE方法的有效性，本文开展了下列计算机仿真实验，对新方法的性能进行验证。Monte Carlo仿真实验采用的是COST 207乡村信道模型，信道参数如表1所示，系统仿真参数如表2所示。

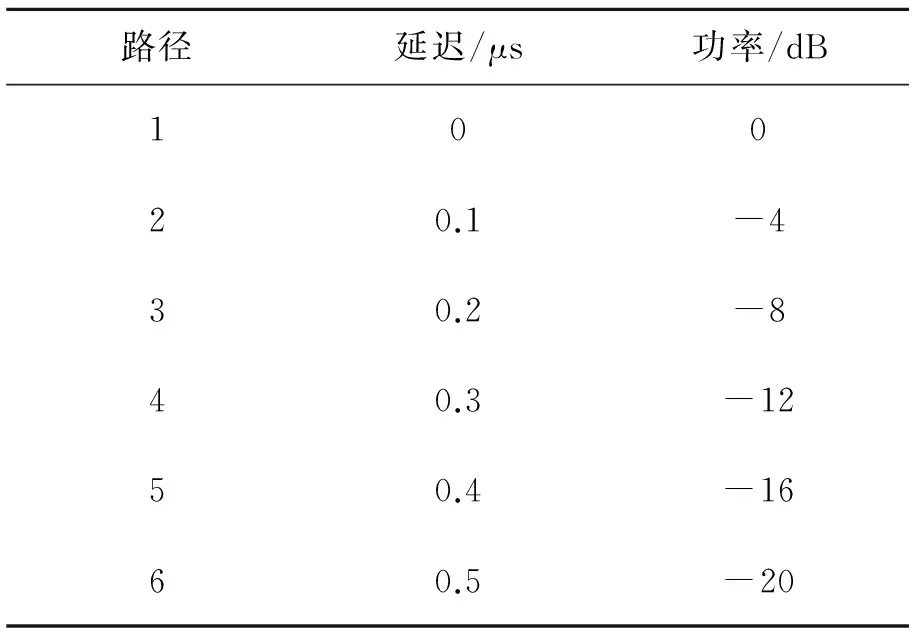
表1　COST 207乡村信道模型

表2　系统仿真参数

信道估计均方误差(MSE)是衡量信道估计算法性能优劣的常用方法，其定义为：

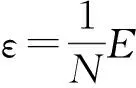
(25)

其中E(·)表示期望运算。

图4为本文提出的TDDSCE方法与其它信道估计方法的结果比较。由图4可知，PN相关信道估计方法的复杂度最低，但其性能在稀疏信道性能较差，存在一个显著的地板效应，难以满足稀疏信道估计要求。最小二乘信道估计方法的性能优于PN序列相关信道估计方法，但由于其忽略了信道的稀疏特性，性能上较差。文献[14]中采用的凸优化算法比传统最小二乘算法和PN相关信道估计方法的性能增益较大，但其计算复杂度高。本文提出的阈值判决信道估计方法在性能上最优，其复杂度略高于LS方法，但远低于文献[14]中的凸优化算法。

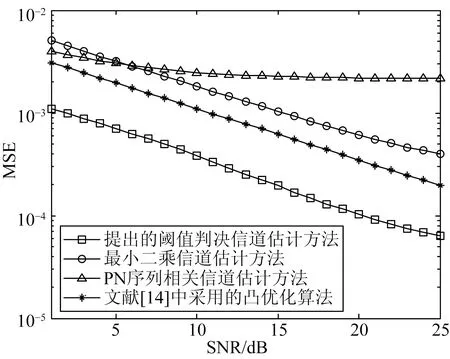
图4　TDDSCE方法的MSE性能

本文提出的TDDSCE稀疏信道估计方法与其它信道估计方法的误比特率对比结果如图5所示。由图5可知PN序列相关信道估计方法的性能差，地板效应十分显著，其与信道估计均方误差结果一致，与PN序列相关方法相比，最小二乘信道估计方法具有较大性能增益，但其在稀疏信道应用时性能较差。文献[14]采用的凸优化算法能够大幅度提高稀疏信道的估计精度，但其计算复杂度高，实际应用严重受限。本文提出的阈值判决稀疏信道估计方法在BER性能上远优于其它信道估计方法，非常接近于信道已知时的情形。在误比特率为10-4时，阈值判决方法比文献[14]中采用的凸优化算法有4 dB 性能增益。在信噪比为20 dB时，新方法的误比特率可达5×10-4，而最小二乘法只能达到3×10-2。

图5　TDDSCE方法的误比特率性能

5　结　论

在高速无线通信时，为充分利用信道的稀疏多径传播特性，本文提出TDDSCE稀疏信道估计方法，将阈值判决过程分解为“粗估计”和“精估计”两部分。通过合理设置判决门限值，强制将幅值小于阈值的信道抽头置零。本文方法的复杂度与最小二乘信道估计方法相当，但其性能远优于传统PN序列相关和最小二乘信道估计方法，基于COST 207典型乡村信道模型的计算机仿真实验结果验证了所提方法的有效性。

[1]DAOUD S， GHRAYEB A. Using resampling to combat doppler scaling in UWA channels with single-carrier modulation and frequency-domain equalization [J].IEEETransactionsonVehicularTechnology， 2016，65(3): 1261-1270.

[2]ZHANG J T， YANG L L， HANZO L，etal.. Advances in cooperative single-carrier FDMA communications: beyond LTE-advanced [J].IEEECommunicationsSurveys&Tutorials， 2015， 17(2): 730-756.

[3]WANG D， ZHAO Q， YANG L. Robust signal-to-noise ratio and noise variance estimation for single carrier frequency domain equalisation ultra-wideband wireless systems [J].IETCommunications， 2015， 9(3): 1598-1605.

[4]COON J， SANDELL M， BEACH M，etal.. Channel and noise variance estimation and tracking algorithms for unique-word based single-carrier systems [J].IEEETransactionsonWirelessCommunications， 2006， 5(6)：1488-1496.

[5]ZHENG Y H， XIAO C S. Channel estimation for frequency-domain equalization of single-carrier broadband wireless communications [J].IEEETransactionsonVehicularTechnology， 2009，58(2): 815-823.

[6]焦现军，张磊，项海格.单载波频域均衡系统中的PN信道估计算法 [J].北京大学学报，2007， 37(1)：103-108.JIAO X J， ZHANG L， XIANG H G. PN based channel estimation in SC-FDE system [J].JournalofBeijingUniversity， 2007， 37(1):103-108. (in Chinese)

[7]李丹萍，刘毅，张海林.MIMO SC-FDE系统的时域信道估计新算法 [J]. 通信学报， 2011， 32(2)：144-149.

LI D P， LIU Y， ZHANG H L.Channel estimation for MIMO SC-FDE systems via time-domain based approaches [J].JournalofCommunications， 2011， 32(2)：144-149. (in Chinese)

[8]SCHNITER P. A message-passing receiver for BICM-OFDM over unknown clustered-sparse channels [J].IEEEJournalofSelectedTopicsinSignalProcessing，2011，5(8):1462-1474.

[9]WANG H， GUO Q， ZHANG G，etal.. Pilot pattern optimization for sparse channel estimation in OFDM systems [J].IEEECommunicationsLetters， 2015， 19(7): 1233-1236.

[10]QI C， YUE G， WU L，etal.. Pilot design schemes for sparse channel estimation in OFDM systems [J].IEEETransactionsonVehicularTechnology， 2015， 64(4): 1493-1505.

[11]HE X， SONG R， ZHU W P. Pilot allocation for distributed-compressed-sensing-based sparse channel estimation in MIMO-OFDM systems [J].IEEETransactionsonVehicularTechnology， 2016， 65(5): 2990-3004.

[12]GAO Z， ZHANG C， WANG Z，etal.. Prior information aided iterative hard threshould: a low-complexity high-accuracy compressive sensing based channel estimation for TDS-OFDM [J].IEEETransactionsonWirelessCommunications， 2015， 14(1):242-250.

[13]孟庆微， 黄建国， 韩晶， 等. 水声单载波分块传输中基于压缩感知的稀疏信道估计方法 [J].北京邮电大学学报， 2012，35(5):14-17.

MENG Q W， HUANG J G， HAN J，etal.. Compressed sensing based sparse channel estimation scheme for underwater single carrier block transmission [J].JournalofBeijingUniversityofPostsandTelecommunications， 2012，35(5):14-17. (in Chinese)

[14]孟庆微， 黄建国， 何成兵， 等. 采用时域测量矩阵的压缩感知稀疏信道估计方法 [J]. 西安交通大学学报， 2012，46(8): 94-99.

MENG Q W， HUANG J G， HE CH B，etal.. An compressed sensing estimation method for sparse channels using time domain measurement matrix [J].JournalofXi’anJiaotongUniversity， 2012，46(8): 94-99. (in Chinese)

孟庆微(1980-)，男，黑龙江安达人，博士，讲师，2007年于空军工程大学获得硕士学位，2013年于西北工业大学获得博士学位，主要从事高速无线通信、水声通信技术的研究。E-mail: qingw_meng@163.com

导师简介：

孟相如(1963-)，男，陕西西安人，教授，博士生导师，1988年、1994年于西安交通大学分别获得硕士、博士学位，1997年在电子科技大学博士后出站，主要从事宽带通信与网络技术研究。E-mail：xrmeng@126.com

(版权所有未经许可不得转载)

基金项目：国家自然科学基金资助项目(No.61175087)；北京工业大学智能机器人“大科研”推进计划“智能服务机器人模块化及实用化关键技术研究”资助项目

文章编号1004-924X(2016)09-2339-08

Threshold decision directed sparse channel estimation for single carrier block transmission

MENG Qing-wei， SU Ling-hua， SU Yu-ze， MENG Xiang-ru*， HUANG Yang-chao(InstituteofInformationandNavigation，AirForceEngineeringUniversity，Xi′an710077，China)*Correspondingauthor，E-mail：xrmeng@126.com

A threshold decision directed sparse channel estimation (TDDSCE) method was proposed for a Single Carrier Block Transmission(SCBT) system， which can take advantage of the sparsity inherent in high rate wireless communication channels， and improve the channel estimation accuracy. Firstly， a pilot sequence was used to perform a least square (LS) channel estimation， then a decision threshold was derived by obtained channel estimated values. The channel taps whose values were smaller than the decision threshold were forced to be zeros， only the channel taps whose values were above the decision threshold were reserved， so that the sparse channel estimation accuracy was greatly improved. A simulation experiment was carried out based on a COST 207 rural area channel profile， and the results show that the performance of proposed method is most close to that of the known channel case， and its bit error rate (BER) reaches 5×10-4when the signal to noise ratio is 20 dB. However， the traditional LS channel estimation method only achieves the BER of 3×10-2. The method improves the sparse channel estimation accuracy and reduces the complexity of the SCBT system， and its feasibility is verified by obtained results.

wireless communication; single carrier block transmission; threshold decision; sparse channel estimation

2016-06-27；

2016-08-01.

国家自然科学基金资助项目(No.61401499，No.61573017，No.61601500)；陕西省自然科学基金资助项目(No.2016JM4008)

1004-924X(2016)09-2332-07

TP911

A

10.3788/OPE.20162409.2332

2016-04-11；修订日期:2016-06-20.