飞行器折叠翼机构展开性能的优化及实验

韩雪峰，刘晓东，马伍元，马　青，袁东明

(中国科学院 长春光学精明机械与物理研究所，吉林 长春 130033)



飞行器折叠翼机构展开性能的优化及实验

韩雪峰*，刘晓东，马伍元，马青，袁东明

(中国科学院 长春光学精明机械与物理研究所，吉林 长春 130033)

为了优化飞行器折叠翼机构的展开性能，对飞行器的折叠翼机构进行分析，并提出了优化其展开性能的方法。建立了折叠翼机构展开的理论模型和动力学仿真模型，对折叠翼机构展开过程进行了动力学分析，并进行了实例计算。分析了影响折叠翼机构展开性能的因素，用正交试验的方法对折叠翼机构进行了优化设计，得到了最优折叠翼机构方案，并对最优方案进行了仿真分析。最后，按照最优方案折叠翼机构进行了改进，实验测试了折叠翼机构的展开性能。实验测得折叠翼机构展开时间为0.128 s，测点位置应力分别为82 MPa和92 MPa；动力学仿真得到折叠翼机构展开时间为0.122 s，相应测点位置应力分别为85 MPa和96 MPa，两项测试误差在5%以内。得到的结果表明折叠翼机构满足机翼展开稳定、快速，应力和冲击力小的要求，为飞行器性能的调高奠定了基础。

飞行器；折叠翼；展开性能；动力学模型；正交试验；结构优化

1　引　言

导弹采用折叠翼机构对提高导弹的运输、储存和对载机的适应性、减小包装箱尺寸等具有重要意义，所以折叠翼导弹受到了越来越广泛的关注。国内外众多型号的导弹采用了折叠翼机构，如美国“宝石路2”的GBU-12、GBU-16、GBU-20，“钻石背”的JDAM和SDB，英法的弹出式尾翼导弹BGL1000，以色列的spice-1000，国内的钻石翼JDAM-雷石6等[1-2]。

折叠翼机构展开性能关系到导弹发射后能否正常飞行和既定任务的完成情况，是折叠翼机构设计的主要依据。折叠翼机构展开性能包括展开时间、展开冲击力和展开同步性等。对于包含折叠翼机构的舵机系统，控制系统的起控时刻要在折叠翼展开完全以后，折叠翼机构的刚度对舵机控制系统的带宽影响较大，折叠翼机构的展开精度对舵机系统的控制能力有较大影响[3-4]。所以对折叠翼机构展开性能的研究具有重要意义，Rahnejat对多体系统运动的建模和方程的理论解进行了详细的研究[5]；RobertKroyer利用有限元软件对折叠翼展开的可靠性进行了分析[6]； YudiHeryawan等人对某折叠翼飞机的设计、制造、风洞试验进行了论述，提出了折叠翼机构的考核验证方法[7]；马彩霞采用压电晶体加速度传感器对某导弹折叠翼的展开时间、展开冲击力、展开角度变化等参数进行了试验测试[8]；李晓辉等以某旋转型火箭弹为例，对折叠翼机构进行了计算和试验对比[9]；崔二巍对某导弹折叠翼机构展开进行了理论分析和数值计算[10]；吴俊全对折叠翼机构进行了动力学仿真和试验[11]；赵俊锋对折叠翼机构展开过程刚柔耦合进行了动力学仿真分析[12]。虽然国内外学者对折叠翼机构展开性能进行了广泛的研究，但没有提出对折叠翼机构设计的优化方法，没有从理论分析到仿真分析和实验验证的闭环设计。

为了分析某飞行器折叠翼机构展开性能并对其进行优化，首先建立了折叠机构的理论模型和动力学仿真模型，并进行了实例计算；然后利用动力学仿真和正交试验相结合的方法对折叠机构进行了优化，得到了最优折叠翼机构方案，并对最优方案进行了动力学仿真分析；最后对最优方案的折叠翼机构展开性能进行了实验测试，并与仿真结果进行了对比。

2　折叠翼机构展开理论模型

折叠翼机构原理如图1所示，主要由翼面、支架、导向杆和弹簧等组成。翼面与导向杆通过螺纹连接，导向杆在弹簧力的作用下在支架滑槽内滑动，滑动轨迹包括旋转运动和直线运动。

图1　折叠翼机构原理图

折叠翼机构展开过程如图2所示，展开过程共分为4个阶段，其中在阶段二又可以分为如图3所示的几个阶段，实际运动时阶段2.2和阶段2.3可能会有几次往复过程，直到旋转速度为零时第二阶段结束。

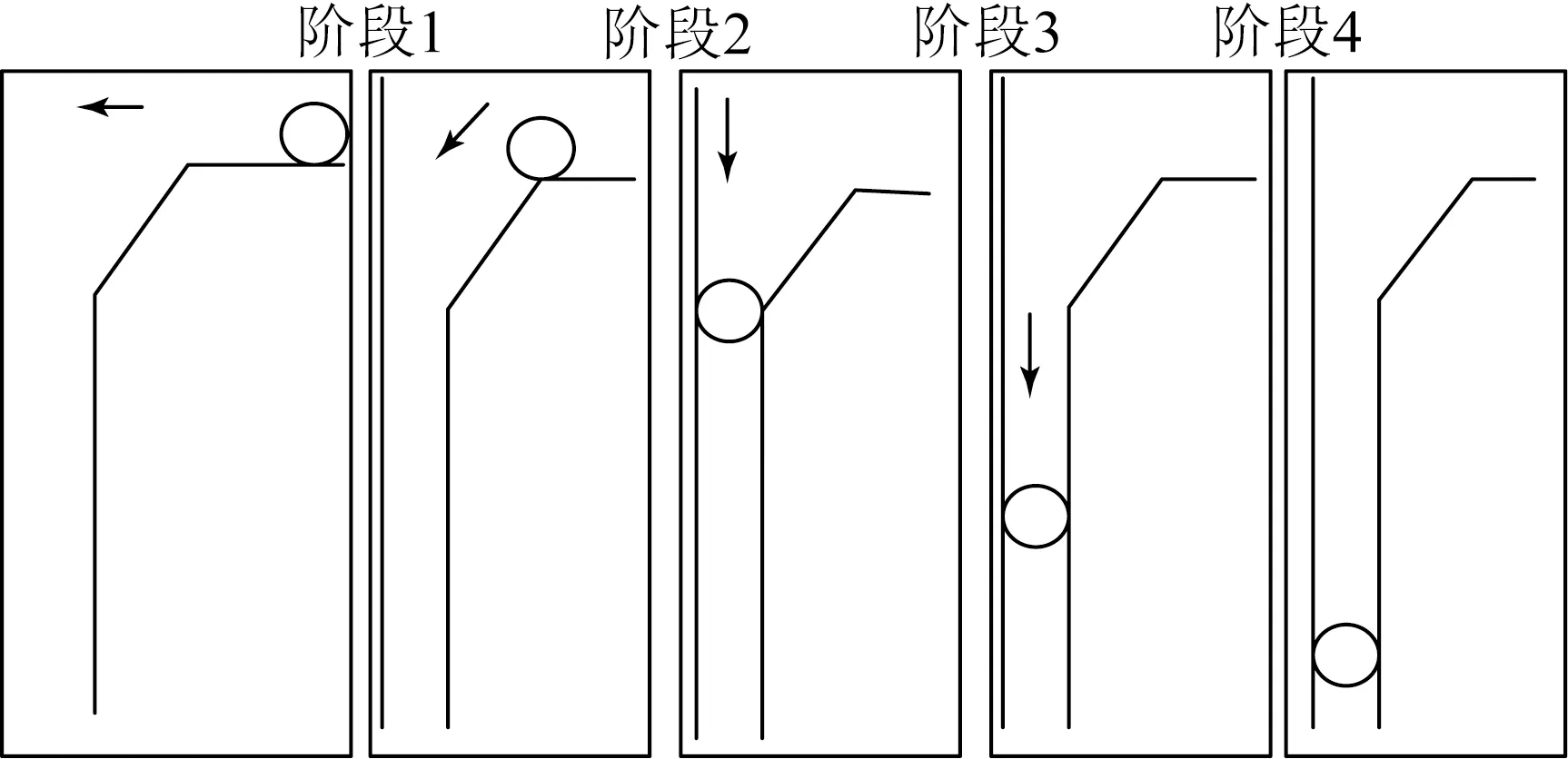
图2　展开过程示意图

图3　第二阶段运动过程示意图

阶段1，从折叠翼释放到导向杆中心运动到端面边缘的过程，所用时间为[0，t1]，前翼在此阶段受到弹簧扭矩Ms、导向杆与支架间摩擦力矩Mf1和翼面与支架间摩擦力矩Mf2的共同作用。为了便于分析折叠翼机构的展开过程，将翼面视为刚体，暂不考虑翼面的弹性变形。根据刚体定轴转动的角动量定理，有：

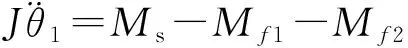
(1)

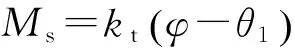
(2)

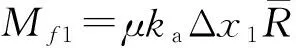
(3)

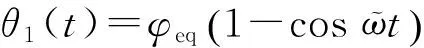
(4)

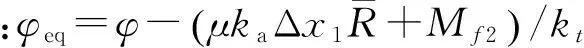
阶段2，运动时间为[t1，t2]，此过程包含翼面的旋转运动和滑移运动，同时包括翼面与滑槽左端面和倒斜面的碰撞往复过程，此阶段运动过程如图3所示，图3给出了一次碰撞往复过程，而实际运动时可能会存在几次往复，往复次数由实际计算结果决定。

阶段2.1，导向杆从端面边缘到第一次碰撞，时间为[t10，t11]。此过程旋转运动方向前翼受到扭簧产生的扭矩Ms和转轴摩擦力矩Mf2，根据角动量定理有：

(5)

θ21(t)=φeq21+A21cos(ϖt)+B21sin(ϖt)，

(6)

其中：参数φeq21、A21、B21可以解得。

滑移运动时翼面受到弹簧力Fs，翼面转轴和支架间滑动摩擦力f1，由牛顿第二定律有：

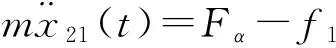
(7)

Fα=kα(Δx1-x21).

(8)

x21=W21(1-cosω(t-t1))，

(9)

其中：W21=Δx1-f1/kα。

阶段2.2，导向杆和支架第一次碰撞到第二次碰撞的过程，时间为[t11，t12]。此过程翼面在旋转运动方向受到扭簧提供的扭矩Ms和转轴摩擦力矩Mf2，根据角动量定理有：

(10)

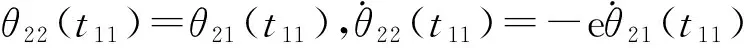
θ22(t)=φeq22+A22cos ϖt+B22sin ϖt，

(11)

其中：参数φeq22，A22，B22可以解得。

滑动方向受力与阶段2.1相同，运动方程如式(9)所示。

阶段2.3，从第二次碰撞到第三次碰撞的运动过程，时间记为[t12，t13]。此过程中前翼旋转受到扭簧扭矩和前翼转轴摩擦力矩，根据角动量定理有：

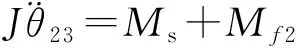
(12)

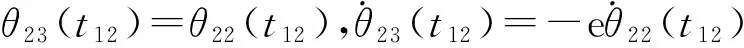
θ23(t)=φeq23+A23cos ϖt+B23sin ϖt，

(13)

其中：φeq23，A23，B23可以解得。

滑动运动受到弹簧推力Fs和翼面转轴与支架间的摩擦力f2，根据牛顿第二定律有：

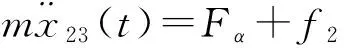
(14)

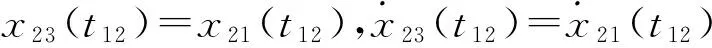
x23(t)=W23+C23cos(ω(t-t1))+

D23sin(ω(t-t1))，

(15)

其中：W23=Δx1+f2/ks，C23，D23可计算得到。

阶段2.4，翼面会重复阶段2.2、2.3，直到旋转运动结束导向杆进入到滑动槽时阶段2结束。

阶段3，导向杆从位置3运动到位置4，时间为[t2，t3]。此过程翼面受到弹簧推力Fa、支架对翼面转轴摩擦力f1、支架对导向杆摩擦力f2，根据牛顿第二定律可得：

(16)

Fa=kα(Δx1-x3).

(17)

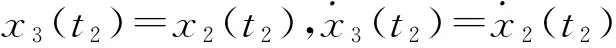
x3(t)=W′+C3cosω(t-t1)+D3sinω(t-t1)，

(18)

其中：W′，C3，D3可计算得到。

阶段4，从翼面接触到锁紧销到展开完成，时间为[t3，t4]。此过程翼面除受到阶段3中的所有力外还受到锁紧销钉给翼面的阻力Fs，根据牛顿第二定律有：

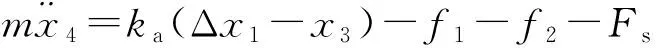
(19)

x4(t)=W″+C4cosω(t-t1)+D4sinω(t-t1)，

(20)

其中：W，C4，D4可计算得到。

带入相关参数，即可得到展开折叠翼展开过程中旋转运动和平移运动随时间的变化。

3　折叠翼机构展开ADAMS仿真模型

3.1翼面建模

由于展开过程中翼面所受冲击载荷较大，翼面在展开过程中会产生变形，进而影响展开性能，为了更加真实的模拟前翼的展开过程和得到展开过程中翼面的最大应力，在ADAMS模型中将翼面做为柔性体进行分析，翼面柔性体建模流程如图4所示[14-15]。

图4　柔性体建模流程图

3.2驱动力矩建模

折叠翼展开驱动力主要由弹簧的预紧力提供，该预紧力提供折叠翼机构展开的扭转力矩和推力，在折叠翼完全展开时，预紧力还有一定的剩余。在建模时用卷簧力矩(Torsion Spring)和拉簧推力(Translational Spring-Damper)来模拟驱动力，扭簧扭矩和拉簧推力计算如式(2)和(8)所示。其中扭簧的初始扭转角φ=140°，扭簧扭转刚度由簧丝直径确定；拉簧的初始压缩量x0=15 mm，拉簧压缩刚度系数同样由簧丝直径确定。

3.3冲击力添加

折叠翼展开过程中存在较多碰撞环节，在ADAMS仿真模型中采用碰撞力(Contact Force)来模拟翼面与支架间和导向杆与支架间的相互碰撞。参数的设置采用推荐值和计算值：其中接触刚度(Stiffness)k根据接触件的材料和截面形状计算确定，指数(Force Exponent)e取2.0，阻尼(Damping)c和切入深度(Penetration Depth)d需要经过有限元仿真来确定[16]。

3.4展开时间确定

折叠翼机构展开过程是转动和平动的叠加，所用时间为从仿真开始到完全展开的时间。在确定平动运动轨迹时，在翼面转轴的中点建立传感器1，通过传感器1得到平动运动位移和速度随时间的变化曲线；在翼面转轴表面建立传感器2和传感器3，通过计算∠213得到翼面转角和角速度随时间的变化曲线。

3.5实际算例

将预估的阻力、阻力矩、碰撞力参数、传感器点参数、几何参数等带入理论模型和ADAMS仿真模型中。理论计算和ADAMS仿真计算结果如图5所示。翼面在旋转运动结束时有一次往复震荡，旋转运动总时间为0.092 s，展开运动总时间为0.129 s；ADAMS仿真结果与理论计算结果相似，同样在旋转运动结束时出现一次震荡，旋转运动总时间为0.102 s，展开运动总时间为0.139 s，仿真结果与理论计算结果较为吻合。

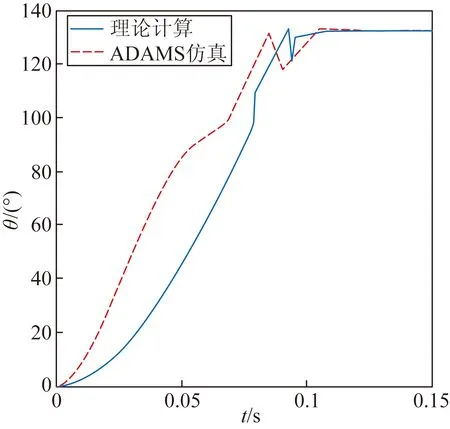
(a)转角随时间变化

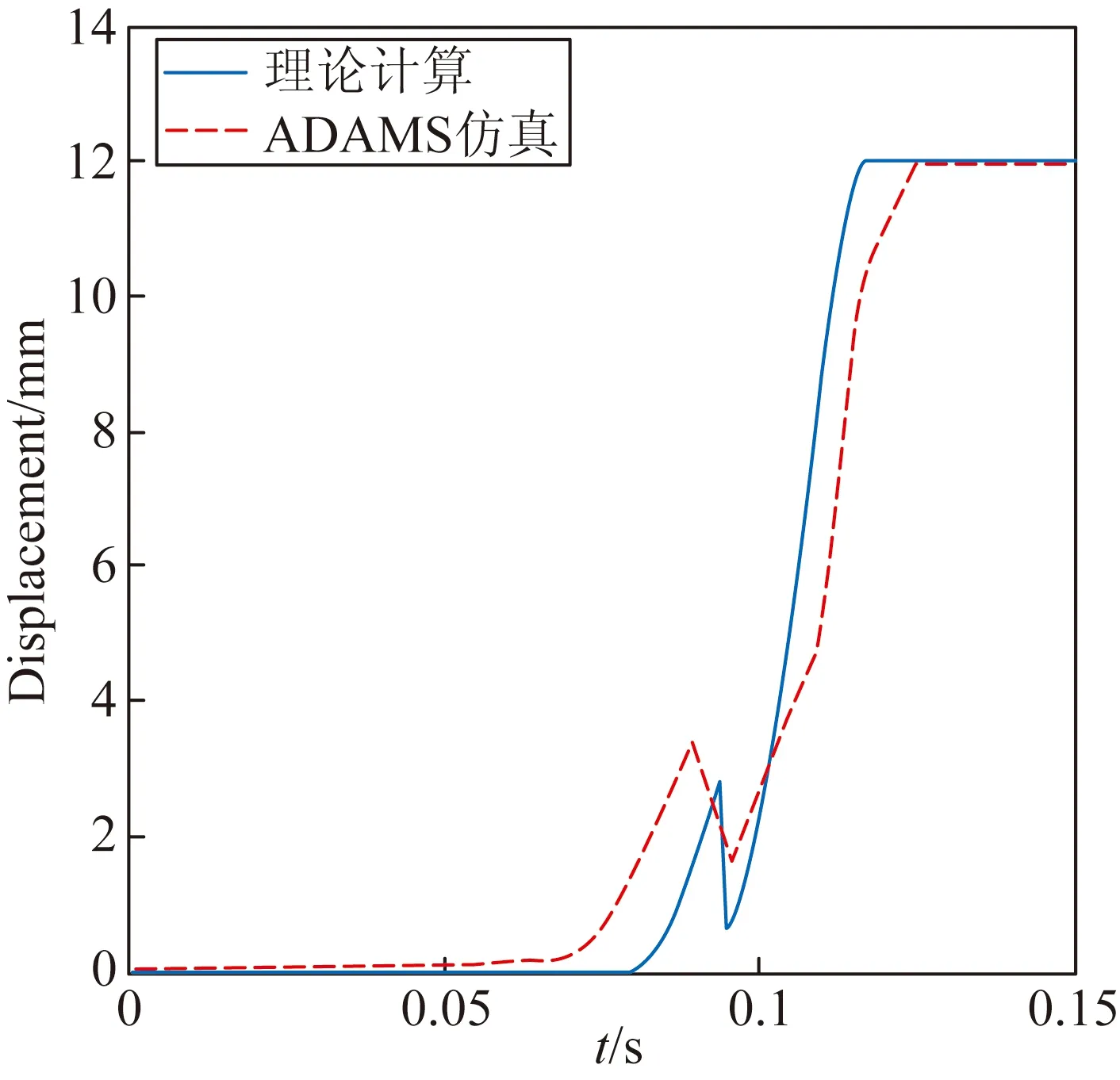
(b)位移随时间变化

4　基于ADAMS仿真的正交试验优化

4.1展开性能影响因素分析

折叠翼机构展开性能指标包括展开时间t、展开最大冲击力F和翼面最大应力δ。其中翼面最大应力和最大冲击力成正比，展开最大冲击力越小性能越好，展开时间越短性能越好。折叠翼机构展开性能影响因素包括弹簧刚度系数、导向杆与支架间配合间隙、翼面材料和导向杆材料。

其中弹簧为折叠机构展开提供动力，直接影响展开时间和展开冲击力；导向杆与支架间配合间隙影响折叠翼在展开过程中导向杆与支架间冲击力；翼面和导向杆使用不同材料，对展开过程中冲击力和摩擦力有较大影响，进而影响折叠机构的展开性能。由于要综合考虑折叠机构的质量特性、加工成本和实际结构形式等，所以只对影响因素取3个水平进行分析。因素水平如表1所示。

如果对上诉影响因素做全面仿真分析，共需要进行81次仿真分析，工作量较大，所以采用4因素3水平正交试验的方法，以减少ADAMS的仿真次数。基于4因素3水平的正交试验只需要9次仿真，是全面仿真的1/9，将大大降低工作量。

表1　因素水平表

4因素3水平仿真方案及仿真结果如表2所示，表2中1、2、3表示对应因素的水平，具体值如表1所示。由表2中的极差R可知，对折叠翼展开时间影响显著性为B>C>D>A，最优运行条件为A3B3C1D1，由此可见对展开时间性能影响显著性排序为弹簧直径、翼面材料、导向杆材料和翼面与支架间间隙量，从仿真结果可以看出展开时间都小于0.2 s，满足对折叠翼所提指标要求；对展开最大冲击力影响的显著性为B>A>D>C，最优运行条件为A3B1C1D3；对折叠翼展开最大冲击力影响显著性排序为弹簧直径、翼面与之间间间隙量、翼面材料和导向杆材料，最大展开冲击力为610 N，满足总体指标要求[17-19]。

可以看出无论从展开时间还是从展开最大冲击力，弹簧直径(刚度)都是最主要的影响因素，弹簧直径越大展开时间越短，展开冲击力越大；翼面材料对展开时间影响比较显著，铝材料展开时间最短；翼面材料对展开冲击力影响不显著，同时用铝材展开冲击力最小，性能最优；翼面和支架间间隙对展开冲击力影响较大，但对展开时间影响很小；导向杆材料对展开时间和展开冲击力影响都不显著，采用镁铝合金材料展开最大冲击力最小，展开时间第二小，采用铝材展开时间最小，展开最大冲击力第二小，考虑到镁铝合金材料强度较高，导向杆决定采用镁铝合金材料。综合考虑以上各因素水平对展开性能的影响，得到最优方案为A3B1C1D3。

表2　正交试验方案及结果

4.2最优方案仿真结果

通过以上分析，得到最优结构方案为A3B1C1D3，即导向杆与支架滑槽间间隙为0.2 mm，簧丝直径1.5 mm，翼面材料用铝合金，导向杆材料用45刚为最优结构方案。将ADAMS模型相关参数改为与最优结构方案对应，仿真得到展开时间为0.124 s，展开过程中翼面和支架间最大冲击力为242 N，导向杆和支架间最大冲击力为245 N，翼面和导向杆与支架间碰撞力变化如图6所示；最大冲击力时刻翼面的应力云图如图7所示，翼面最大应力为170 MPa，最大应力节点为翼面与导向杆连接处，在翼根处最大应力为96 MPa，均小于铝合金的许用应力。

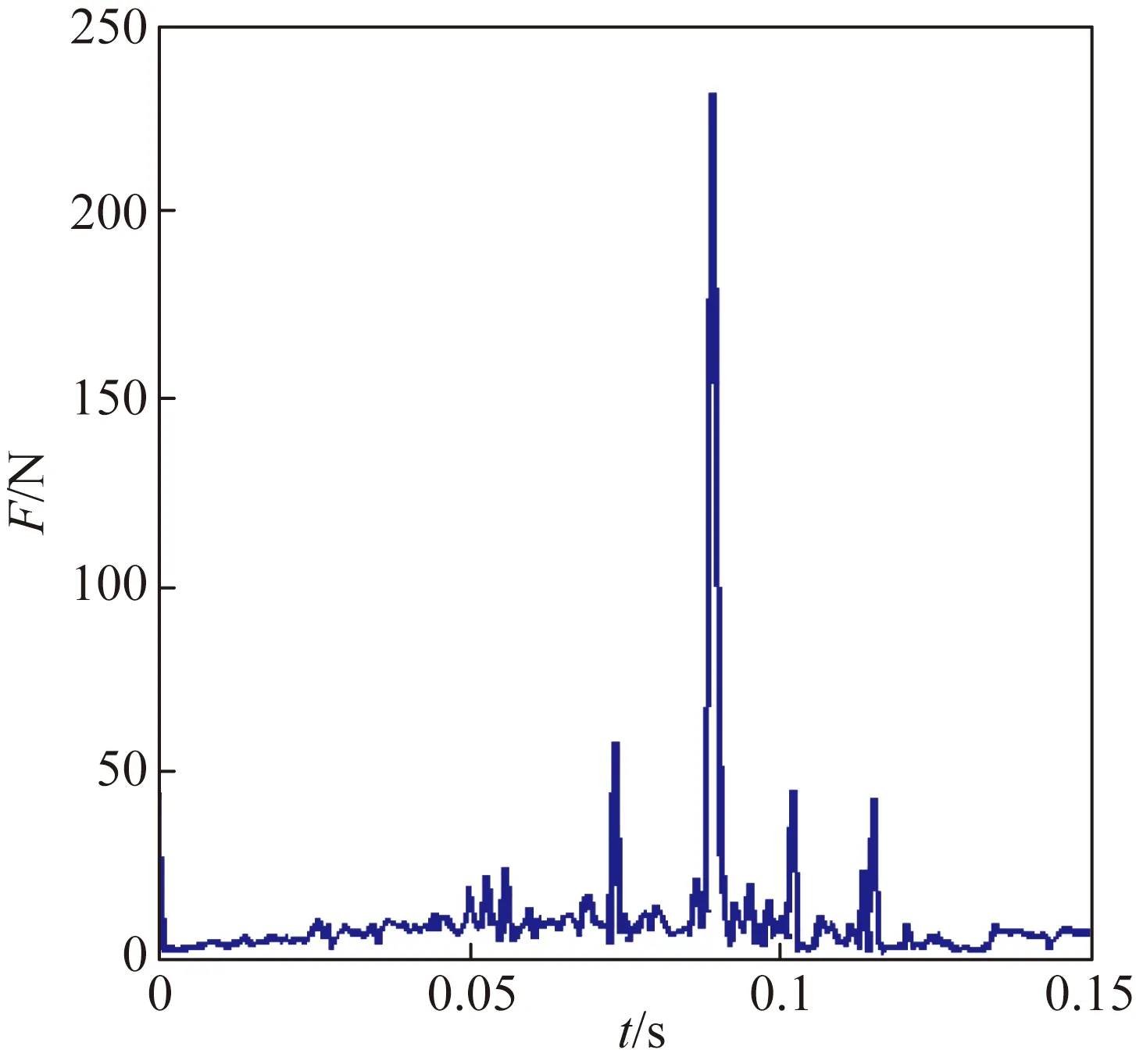
(a)翼面支架间碰撞力

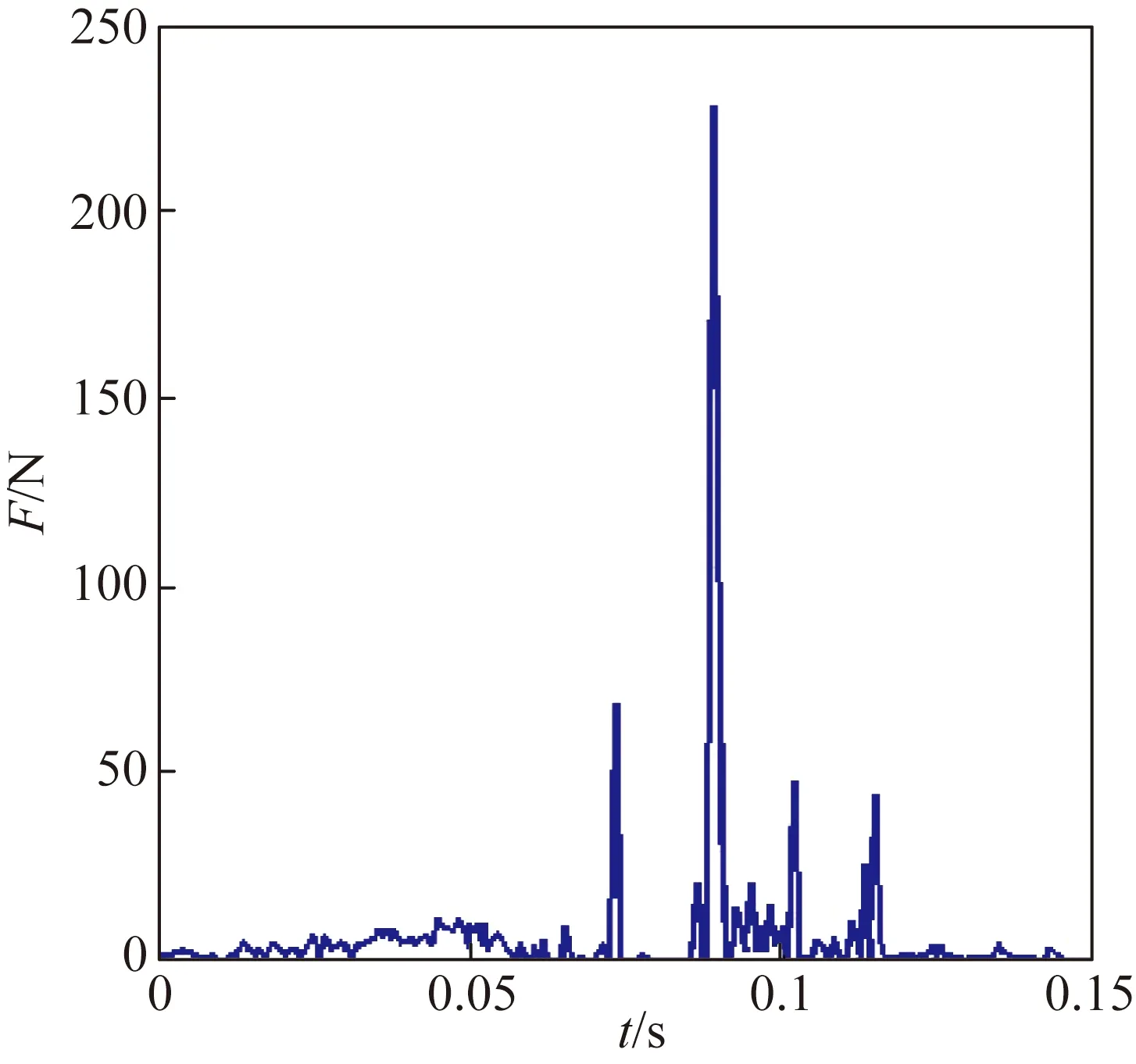
(b)导向杆支架间碰撞力

图7　翼面应力分布云图

5　折叠翼机构展开实验

5.1展开实验描述

折叠翼机构展开实验主要目的是测量折叠翼机构的展开时间和翼面应力。按照最优结构方案，对折叠翼机构进行设计和加工，然后进行折叠翼展开实验。将折叠翼机构固定于实验台上，如图8(a)所示。使用高速摄像机测量折叠翼机构展开时间。

折叠翼机构展开应变测量，折叠翼机构应变片黏贴位置如图8(b)所示，将应变片连接在动态应变仪上，动态应变仪连接在电脑上。通过动态应变仪可以测得折叠翼机构展开过程中的最大应变值。

(a)试验照片

(b)应变片位置照片

5.2实验结果分析

通过分析高速摄像和动态应变仪记录的折叠翼机构展开数据，得到折叠翼机构展开实验结果与ADAMS仿真结果对比如表3所示。通过表3可以看出，展开时间的仿真结果与实验结果误差在5%以内。通过实验得到测点1和测点2处的应力值分别为82 MPa和92 MPa，仿真结果中对应的测点1和测点2位置处的应力值分别为85 MPa 和96 MPa，误差在5%以内。

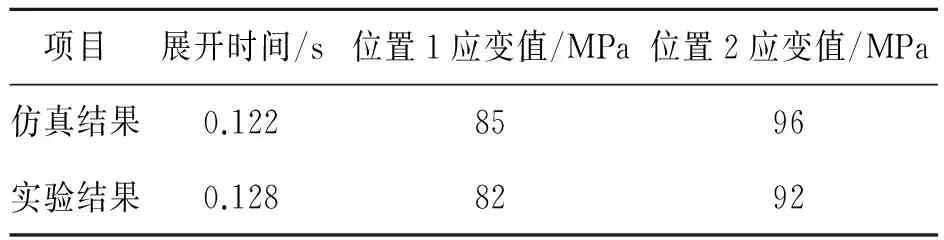
表3　实验和仿真结果对比

6　结　论

为了分析某飞行器折叠翼机构展开性能，本文首先建立了折叠翼机构展开的理论模型和ADAMS仿真模型，对比了两种方法计算得到的折叠翼展开时间，两种方法计算结果误差在5%以内。然后用ADAMS仿真和正交试验相结合的方法，对折叠翼机构进行了优化，得到了最优折叠翼机构方案。用ADAMS对最优结构方案进行了动力学分析，展开时间为0.122 s，展开最大冲击力246 N，展开翼面最大应变180 MPa，翼面根部节点应力分别为85 MPa和96 MPa。最后通过实验对折叠翼机构的展开性能进行了测试，实验测得展开时间0.128 s，翼面根部的应变分别为82 MPa和92 MPa，与仿真结果相比误差在5%以内。实验结果表明折叠翼机构满足展开稳定可靠、时间短、冲击力小的要求，为飞行器性能提高提供了参考。

[1]周义，周绪斌，王自焰.“宝石路”激光制导炸弹风雨四十载[J].兵器博览，2006(2)：5-9.

ZHOU Y， ZHOU X B， WANG Z Y.“Gem” laser guided bombs and wind and rain forty years [J].WeaponExpo.，2006(2):5-9.(in Chinese)

[2]丁红.某导弹折叠翼的有限元分析与试验研究[D].哈尔滨：哈尔滨工程大学，2010.

DING H.FiniteElementAnalysisandExPerimentalStudyforAfoldingWingofAircraftmissiles[D].Harbin: Harbin Engineering University，2010.(in Chinese)

[3]张明月，杨洪波，章家保.改进自抗扰控制谐波式电动舵机伺服系统[J].光学 精密工程，2014，22(1):99-106.

ZHANG M Y， YANG H B， ZHANG J B. Servo system of harmonic drive electromechanical actuator using improved ADRC [J].Opt.PrecisionEng.，2014，22(1)：99-106.(in Chinese)

[4]肖前进，贾宏光，章家保，等.电动舵机伺服系统非线性辨识及补偿[J].光学 精密工程，2013，21(8)：2038-2046.

XIAO Q J， JIA H G， ZHANG J B，etal.. Identification and compensation of nonlinearity for electromechanical actuator servo sysem [J].Opt.PrecisionEng.，2013，21(8)：2038-2046.(in Chinese)

[5]ROBERT K. Wing mechanism analysis [J].ComputersandStructures， 1999， 72(8):253-265.

[6]YUDI H， HOON C P， NAM S G. Byun Design and demonstration of a small expandable morphing wing [J].Proc.ofSPIE， 2005， 57(14):224-231.

[7]METOM S.Piezoelectrically actuated four-bar mechanism with two flexible links for micromechanical flying insect thorax [J].IEEE/ASMETransactionsonMechatronics，2003，104(1):299-305.

[8]马彩霞，余旭东，王涛.导弹折叠翼展开运动试验[J].弹箭与制导学报，1993(2):63-65.MA C X，YU X D， WANG T.Missile folding wing exercise testing [J].JournalofProjectiles，Rockets，MissilesandGuidance，1993(2):63-65.(in Chinese)

[9]李晓晖，李怀念，吴俊全.火箭弹折叠翼展开过程的计算与试验研究[J].航天器环境工程，2009，26：82-86.

LI X H， LI H N， WU J Q.Calculation and experimental study on the folding wing of rocket projectile [J].SpacecraftEnvironmentEngineering， 2009，26:82-86.(in Chinese)

[10]崔二巍，于存贵，李猛，等.某导弹折叠弹翼展开过程的仿真分析[J].兵工自动化，2013，32(12)：12-15.

CUI E W， YU C G， LI M，etal..The simulation analysis of the wing of a missile folding wing [J].OrdnanceIndustryAutomation，2013，32(12)：12-15.(in Chinese)

[11]吴俊全，孙海文，张晓.折叠翼展开试验与动力学仿真研究[J].弹箭与制导学报，2012，32(3)：164-167.

WU J Q，SUN H W，ZHANG X.The researchon unfolding testand dynamic model of folding-wing [J].JournalofProjectiles，Rockets，MissilesandGuidance，2012，32(3)：164-167.(in Chinese)

[12]赵俊锋，刘莉.折叠弹翼展开的刚柔耦合动力学分析[J].弹箭与制导学报，2011，31(5)：141-146.

ZHAO J F， LIU L. Dynamic simulation and optimization design of folding wing deployment [J].JournalofProjectiles，Rockets，MissilesandGuidance，2011，31(5)：141-146.(in Chinese)

[13]R.克拉夫，J.彭津，王光远(译).结构动力学[M].北京：高等教育出版社，2006.

CLOUGH R W，PENZIEN J，WANG G Y(Translation).StructuralDynamics[M]. Beijing: Higher Education Press， 2006.(in Chinese)

[14]金光，谢晓光，谷松.卫星太阳能帆板展开的动力学仿真分析和应用[J].光学 精密工程， 2014，22(3)：745-751.

JIN G，XIE X G，GU S.Dynamic simulation and application of deploy able mechanism of satellite solar panels [J].Opt.PrecisionEng.，2014，22(3)：745-751.(in Chinese)

[15]郑黎明，邓春萍，杨慎华.激光切割头摆动机构的动力学仿真及试验[J].光学 精密工程，2009，17(12):3047-3054.

ZHENG L M， DENG CH P， YANG ZH H.Dynamic simulation and application of deployable mechanism of satellite solar panels [J].Opt.PrecisionEng.，2009，17(12):3047-3054.(in Chinese)

[16]黑沫，鲁亚飞，张智永.基于动力学模型的快速反射镜设计[J].光学 精密工程，2013，21(1):53-61.

HEI M， LU Y F， ZHANG ZH Y.Design of fast steering mirror based on dynamic model [J].Opt.PrecisionEng.，2013， 21(1):53-61.(in Chinese)

[17]黄蓉姿，万金泉，马邕文.正交实验选择纤维素酶产生菌的最优综合培养条件[J].中国环境科学，2012，32(1):130-135.

HUANG R Z， WAN J Q， MA H W.Optimization of synthetic culture condition ofcellulose producing strains using orthogonal experimental design [J].ChinaEnvironmentalScience，2012，32(1):130-135.(in Chinese)

[18]柳贡慧，刘伟，刘忠.利用四因素三水平正交回归分析法进行钻具造斜率预测研究[J]. 石油天然气学报，2010，32(3):108-112.

LIU G H， LIU W， LIU ZH. Using the four factor three level orthogonal regression analysis method to study the prediction of drilling string [J].JournalofOilandGasTechnology，2010，32(3):108-112.(in Chinese)

[19]郑新毅，贾振元，任小涛.用正交试验分析电参数对小孔圆柱度的影响[J].光学 精密工程，2010，18(2):426-433.ZHENG X Y， JIA ZH Y， REN X T.Analysis on effect of discharge parameters on cylindricity of small holes by orthogonal experiments [J].Opt.PrecisionEng.，2010，18(2):426-433.(in Chinese)

韩雪峰(1982-)，男，吉林公主岭人，副研究员，2006年于吉林大学获得学士学位，2011年于中国科学院长春光学精密机械与物理研究所获得博士学位，主要负责结构总体工作，从事飞行器结构动力学和机电一体化协同优化研究。E-mail: hanxuefeng5210@163.com

刘晓东(1990-)，男，黑龙江齐齐哈尔人，硕士，研究实习员，2012年于吉林大学获得学士学位，2014年于哈尔滨工业大学航天学院获得硕士学位，主要从事飞行器结构设计工作。E-mail: xiaodonglly@126.com

(版权所有未经许可不得转载)

Optimization and experiments of deployment performance for folding wing mechanism of an aircraft

HAN Xue-feng*， LIU Xiao-dong， MA Wu-yuan， MA Qing， YUAN Dong-ming

(ChangchunInstituteofOptics，FineMechanicsandPhysics，ChineseAcademyofSciences，Changchun130033，China)*Correspondingauthor，E-mail：hanxuefeng5210@163.com

To optimize the deploying performance of folding wing mechanism for an aircraft， this paper analyzes the folding wing mechanism and proposes a method to optimize the deploying performance of the mechanism. A theoretical model and a dynamic simulation model for the deployment of folding wing mechanism were established， the deploying processing of folding wing mechanism was analyzed and the folding time of the mechanism was given by using the theoretical model. Then， the effect factor on the deploying performance of the mechanism was analyzed， and the orthogonal trial method was used to optimize those structure parameters to obtain a optimized designed scheme. Finally， the mechanism was simulated and optimized by the optimal scheme and the deploying performance of the mechanism was measured by experiments. Experimental results show that the folding time of the mechanism is 0.128 s and the structure stresses at the measuring points are 92 MPa and 80 MPa respectively. Moreover the dynamic model test results of the mechanism show that the folding time of the mechanism is 0.12 s and the structure stresses at the measuring points are 85 MPa and 96 MPa， respectively. The difference of the experimental and simulation results is within 5%. It indicates that the optimal folding wing mechanism promotes the flight performance of the aircraft while the mechanism also basically satisfies the design requirements like the stability， reliability， fast speed， small stress and the impact force.

aircraft; folding wing; deployment performance; dynamic model; orthogonal trial; mechanism optimization

2016-01-17；

2016-02-10.

中国科学院国防科技创新基金资助项目(No.YYYJ-1122)

1004-924X(2016)09-2262-09

V224

A

10.3788/OPE.20162409.2262