微机电陀螺耦合刚度的辨识

陈志勇，刘悦琛，张　嵘，周　斌

(清华大学 精密仪器系，北京 100084)



微机电陀螺耦合刚度的辨识

陈志勇*，刘悦琛，张嵘，周斌

(清华大学 精密仪器系，北京 100084)

针对微机电陀螺耦合刚度的辨识，提出了以驱动轴、检测轴、驱动-转动耦合和驱动-检测耦合频率响应特性为基础的耦合刚度辨识方法。设计了一种驱动轴和检测轴双向位移解耦的双质量线振动微机电陀螺，基于经过简化的梁的刚度特性建立了微陀螺平面运动动力学方程，导出了结构在存在耦合刚度情况下驱动轴、检测轴、驱动-转动耦合和驱动-检测耦合的传递函数。根据耦合传递函数把刚度耦合产生的根源定位到特定的几组梁之间的刚度误差。通过驱动-转动耦合与驱动轴幅频特性之比辨识出驱动-转动耦合刚度系数，通过驱动-检测耦合与检测轴幅频特性之比辨识出转动-检测耦合刚度系数。实验测试了设计加工的微陀螺的频率响应特性，利用提出的耦合刚度辨识方法得到陀螺的驱动-转动和转动-检测耦合刚度系数分别为0.14 N和0.054 33 N。得到的耦合刚度的辨识结果可为微陀螺梁刚度的激光修调提供参数依据。

微机电陀螺；耦合刚度；辨识方法；模型；频率响应

1　引　言

微机电振动陀螺敏感结构的力学原理、静电场作用和加工误差等因素，会导致驱动轴的驱动力或运动传递到检测轴，使检测轴发生振动，从而在敏感轴无角速度的情况下输出信号。一般称这种现象为“耦合”，并用“耦合误差”来定量描述耦合的大小。耦合误差会随温度、气压等发生变化，导致陀螺的零位漂移。因此在结构设计、加工、修调和真空封装等方面都需要做工作以减小耦合误差。

文献[1]讨论了影响陀螺零偏稳定性的多种因素，在机械耦合误差方面计算了刚度耦合误差等效的输入角速度，认为可以通过降低驱动轴谐振频率、增大梁宽和减小相对刚度耦合系数来降低耦合刚度误差。文献[2]提出了一种单质量线振动微机电陀螺敏感结构设计，具有驱动到检测和检测到驱动双向解耦的特性，推导了结构中几字形梁的刚度矩阵，给出了几字形梁轴向刚度和主变形刚度。在结构设计方面要降低刚度耦合，通常采用以互相垂直的梁隔离微机电陀螺的驱动器、检测器和敏感质量的方法[3-6]。文献[7]对双质量线振动陀螺用能量法推导了梁的刚度，建立了结构的刚度矩阵，推导了正交耦合系数的计算公式。文献[8]研究了音叉式陀螺在刚度不对称情况下其耦合结构对陀螺振动特性的影响。文献[9]研究了非解耦陀螺的模态耦合误差，对加工误差与耦合误差的关系进行了仿真，对采用激光修形降低耦合误差的方法进行了仿真和实验，证明了该方法的有效性。也有学者设计正交误差校正方法，通过设计校正结构产生静电力抵消弹性耦合力，从而抑制正交运动[10-12]。

综上，降低结构刚度耦合的主要途径是解耦结构设计、加工误差的激光修调和静电力校正。其中结构修调需要确定修调的位置和修调量的大小，这就需要完成对刚度耦合误差的辨识。

本文研究了微机电陀螺的刚度耦合。设计了驱动轴和检测轴双向位移解耦的双质量线振动微机电陀螺，建立了刚度耦合条件下的平面运动动力学模型。研究了驱动轴、检测轴、驱动-转动耦合及驱动-检测耦合4种频率响应特性之间的关系，提出了耦合刚度系数辨识方法。试验测试了陀螺的振动特性和耦合特性，与刚度耦合模型对比，得到了刚度不对称系数和耦合刚度系数，为结构修调提供了定量依据。

2　微机电陀螺敏感结构设计

2.1双质量线振动解耦结构

双质量敏感结构如图1所示，结构完全对称，主要由以下几个部分组成：(1) 敏感质量块。(2) 驱动梳齿和驱动振动检测梳齿。驱动梳齿置于内部，对称的两组外部驱动检测梳齿可以检测驱动方向的平动和转动量，均采用变重叠面积式梳齿电容。(3) 检测梳齿和平衡力加载梳齿。检测梳齿采用变间隙式，以增大检测和加力效率。(4) 支承梁。2个敏感质量块通过内驱动副梁和内检测副梁分别连接到驱动动齿和检测动齿。驱动动齿和检测动齿再分别通过外驱动梁和外检测梁连接到与玻璃基片固定的锚点。两个质量块在驱动方向上的运动通过驱动主梁相互耦合，在检测方向上的运动通过检测主梁相互耦合。

几字形梁的轴向刚度远高于其主要变形方向上的刚度[2]，所以此双质量陀螺结构驱动运动与检测运动被几字形梁隔离，可以实现双向解耦。

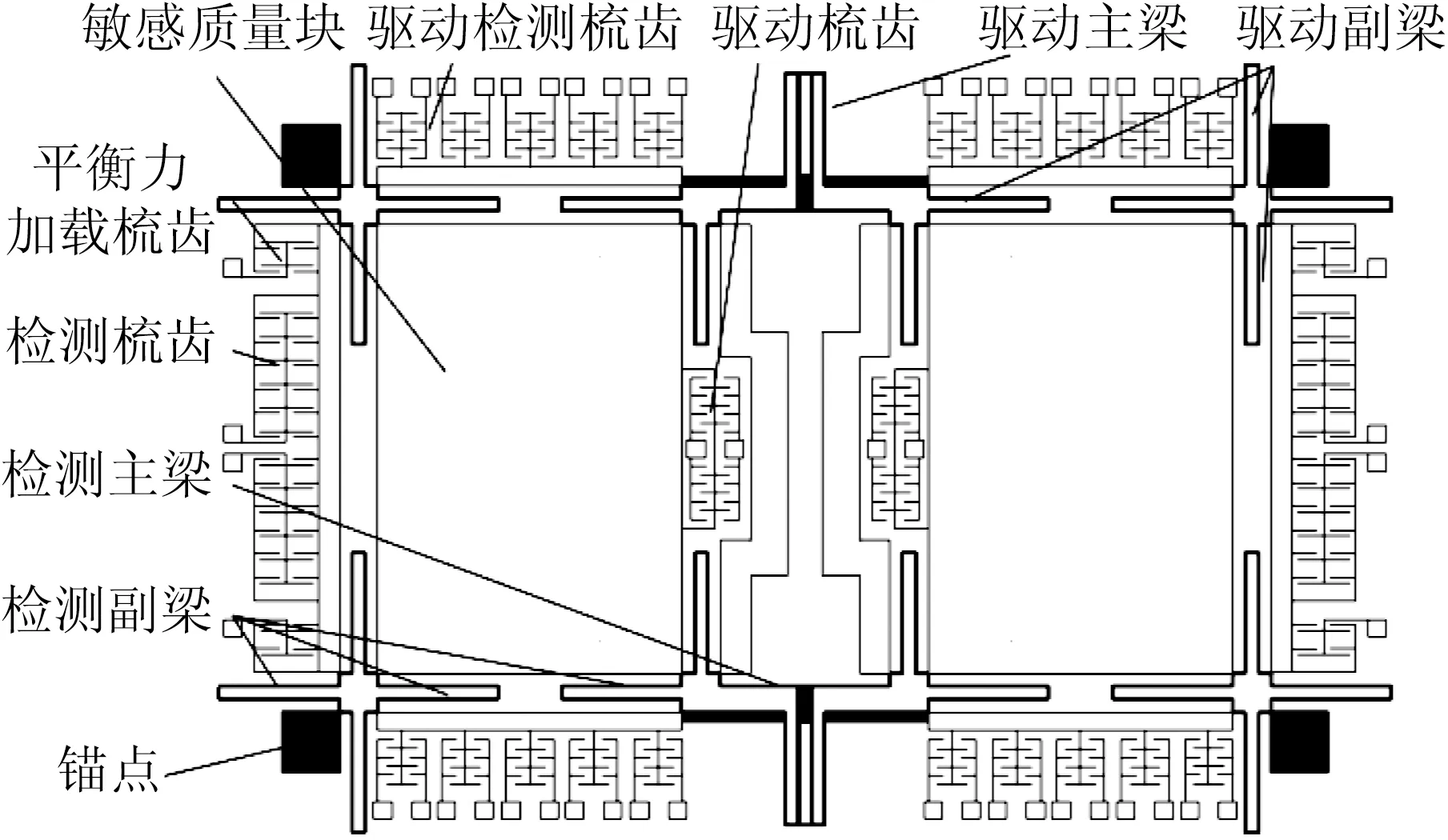
图1　双质量陀螺敏感结构示意图

由图1可见，陀螺的驱动轴和检测轴在动力学上相似。以驱动轴为例，先只考虑结构的平面平动自由度。m1表示一个质量块及与其一起运动的梳齿的质量，且假设两个振子质量相等，x1、x2分别表示两质量块位移的平均值和差值，f1、f2分别表示作用在两质量块上外力的平均值和差值。两个振子同向和反向运动时有效的弹簧刚度和阻尼系数都不同，分别以k1、k2和b1、b2表示。则有：

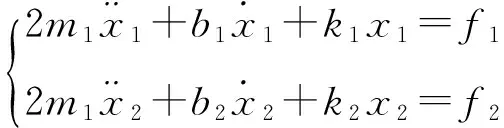
(1)

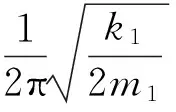
由于结构复杂，关于结构平面转动和在垂直于平面方向的运动自由度的严格的动力学模型难以用方程表达，一般均采用软件仿真的方法得到其力学特性。

2.2模态仿真分析

利用Ansys软件进行了结构的振动模态仿真以验证结构的全解耦特性，并确定结构尺寸参数。最终确定的结构尺寸参数如表1所示，模态振型仿真结果如图2所示，模态频率仿真结果如表2所示。

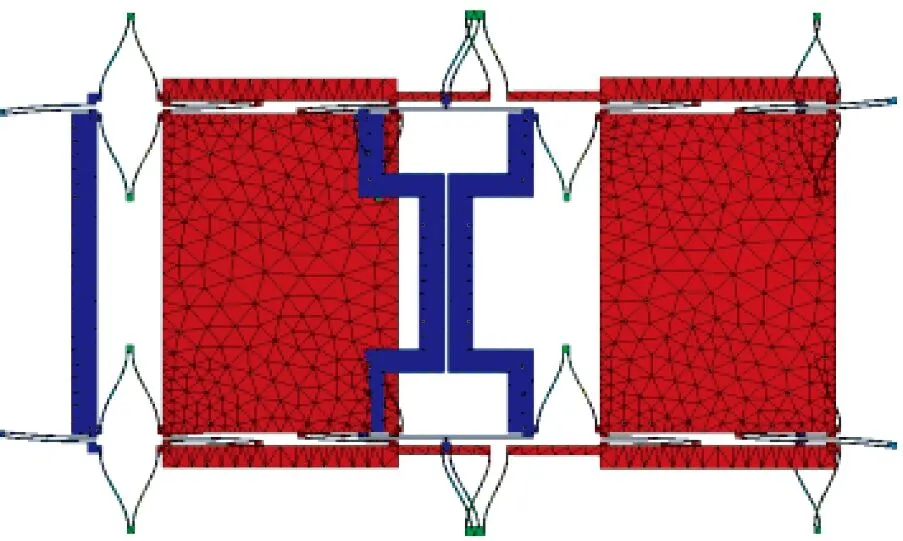
(a)第1模态(a) 1st mode　(b)第2模态(b) 2nd mode

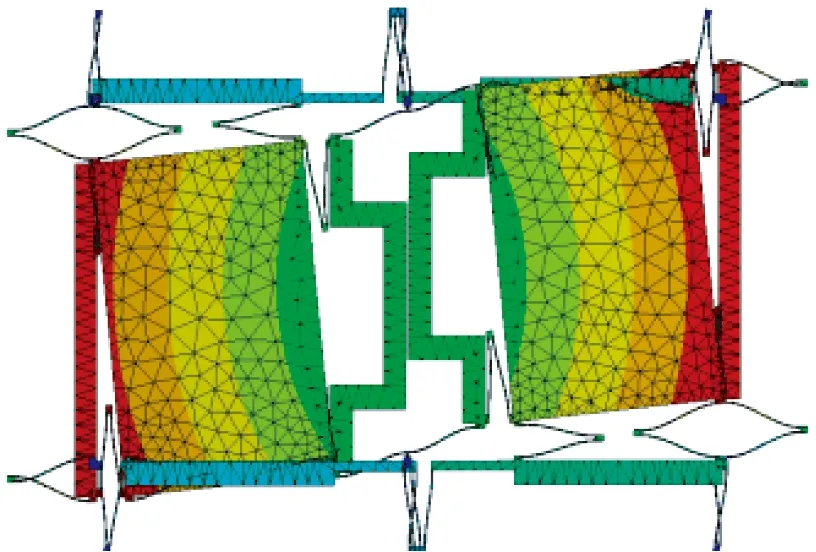
(c)第3模态(c) 3rd mode　(d)第4模态(d) 4th mode

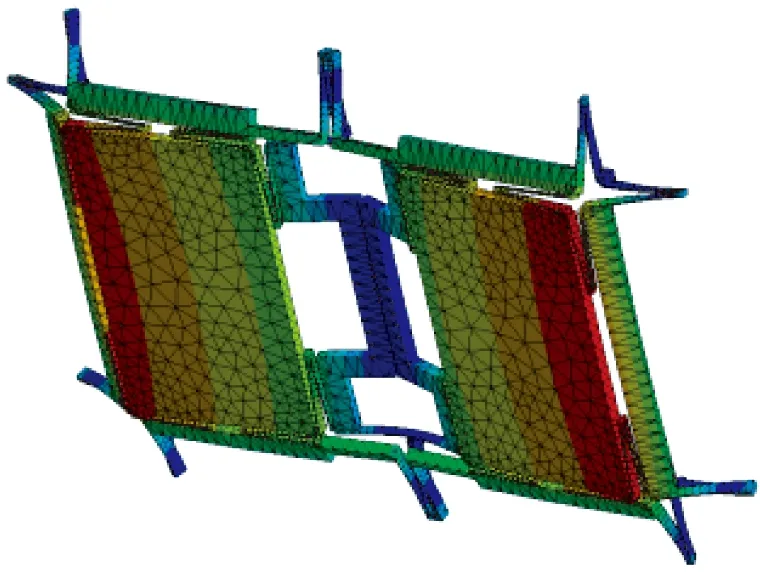
(e)第5模态(e) 5th mode　(f)第6模态(f) 6th mode

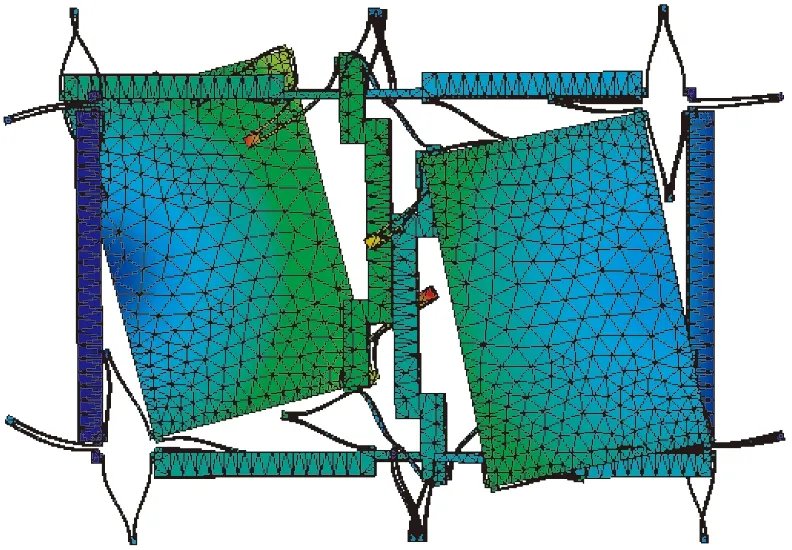
(g)第7模态(g) 7th mode　(h)第8模态(h) 8th mode

结构参数数值/μm结构参数数值/μm厚度80敏感质量块2100×1400驱动主梁长465驱动副梁长482检测主梁长460检测副梁长475所有梁宽10驱动轴梳齿间隙4.5检测轴梳齿小间隙5检测轴梳齿大间隙13

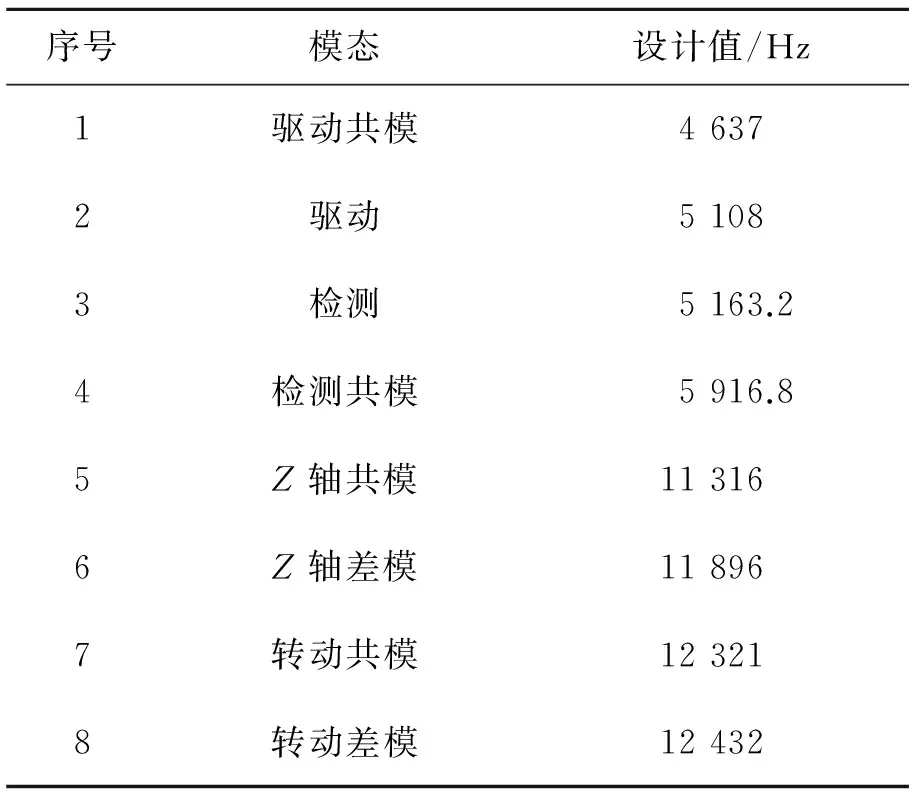
表2　振动模态频率设计值

图2中第1和第4模态分别为质量块在x和y方向的同向振动，与式(1)的第1行对应。第2和第3振动模态分别为质量块在x和y方向上的反向振动，与式(1)的第2行对应，把它们分别作为陀螺工作的驱动模态和检测模态。

由图2(b)可见，在驱动模态下，没有明显的检测模态运动。由图2(c)可见，在检测模态下，单独看上、下驱动检测梳齿，有x方向平动，但是同一质量块对应的上、下两部分梳齿运动方向相反，所以它们的平均值，或者说质量块的质心在x方向的位移相对于y方向位移较小。由此验证了驱动、检测运动是双向解耦的。

敏感结构的加工由北京大学微电子研究院MEMS研究中心完成，实际加工结构如图3所示，敏感结构的整体尺寸为5.7 mm×4.2 mm。

图3　敏感结构照片

3　刚度耦合模型

要建立尽可能完整精确的微机电陀螺的动力学模型，需考虑非常多的细节，比如梁的宽度误差、梁的截面形状、梁在各个方向上的垂直度，结构的厚度误差、质量块的质心误差等误差因素。但容易测量到的实际结构振动频率响应特性有限，因而无法通过这几种响应特性辨识所有的结构误差。另一方面，用激光修调结构耦合误差的方法只能通过调整梁的厚度来改变梁的刚度。因此，需要建立简化的结构动力学模型，以便通过实测的振动特性确定梁的刚度的综合误差。

3.1梁模型的简化

陀螺结构中的梁大多为几字形折叠梁，检测主梁为一字形梁。参考图4和文献[2]，在实际约束条件下，梁在x和y方向的刚度分别为：

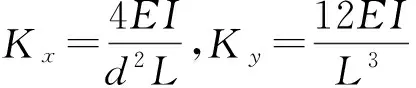
(2)

其中：y为主变形方向，d为梁中心距，L为梁长，E为材料的弹性模量，I为发生主变形时梁截面的惯性矩。

则梁的轴线方向刚度与主变形刚度之比为：

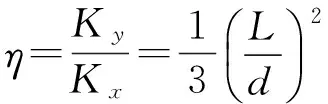
(3)

由于L≫d，所以支承结构的轴向变形刚度远大于主变形刚度。例如L=480 μm，d=10 μm，则η=768。所以，为了简化梁的模型，可以忽略梁的轴向变形。

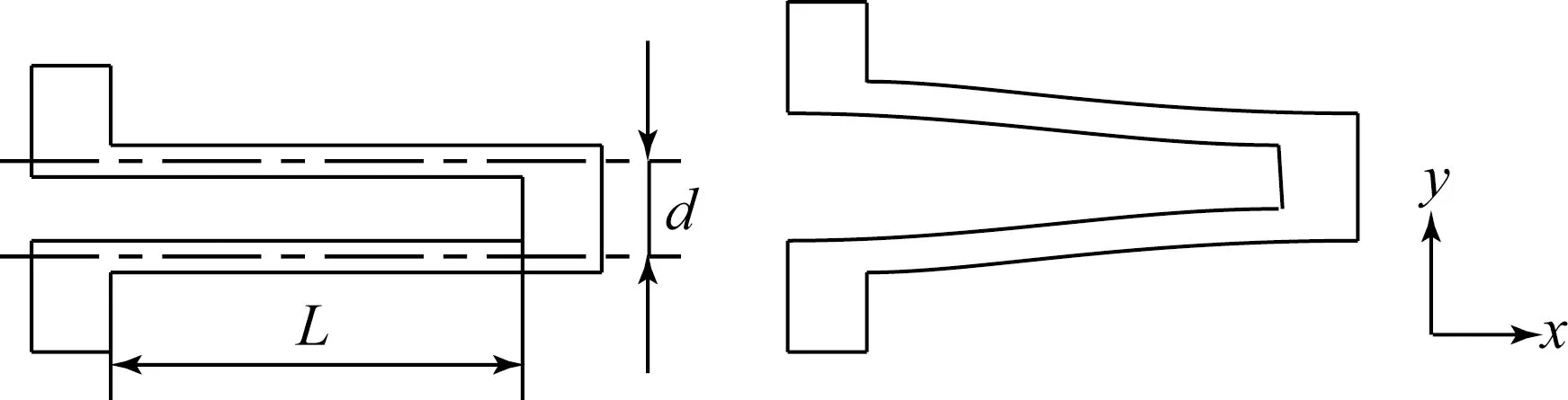
图4　几字梁

3.2结构的平面运动动力学方程

由于结构的完全对称性，分析时可以仅考虑一个质量块。陀螺在x-y平面内具有3个主要运动模态，分别为沿x、y方向的平动及绕z轴旋转运动模态。

结构参数定义如图5所示，mc为敏感质量，将4个梳齿电极等效为4个质量块，其中mdc和msc分别是驱动轴和检测轴单边梳齿的质量。ki(i=1，2，…，16)为各个梁的刚度。敏感质量块的支撑点距离质心的距离在x轴和y轴上的投影以w和l表示。

由于忽略了梁在非主变形方向上的变形，故认为驱动梳齿在检测方向上和检测梳齿在驱动方向上的位移均为0，并且不发生转动。则5个质量块平面运动的总自由度数由15减少为7个：以x、y和θ分别表示敏感质量块沿x，y方向的平动位移和绕着质心的转动位移，x1、x2分别为上下驱动梳齿沿x方向的位移，y1、y2分别为左右检测梳齿沿y方向的位移。

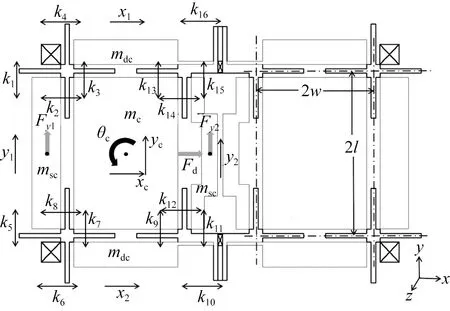
图5　 参数定义

同样由于上述梁的变形假设，中心质量块每个边沿边长方向的位移与其临近的可动梳齿的位移是相同的，即这7个自由度之间存在如下关联：

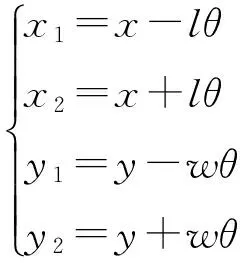
(4)

单边敏感结构简化后的动力学模型具有3个自由度。敏感角速度Ωz=0时陀螺的运动微分方程为：

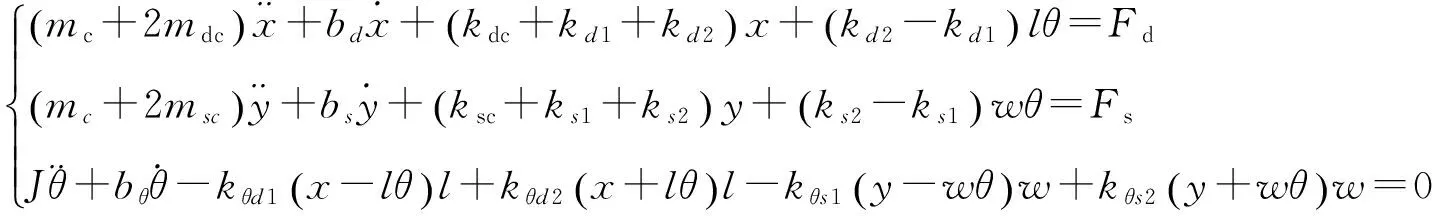
(5)

其中：bd、bs和bθ分别为驱动、检测和转动方向的阻尼系数，J为敏感质量关于其质心绕z方向的转动惯量，其刚度系数为：

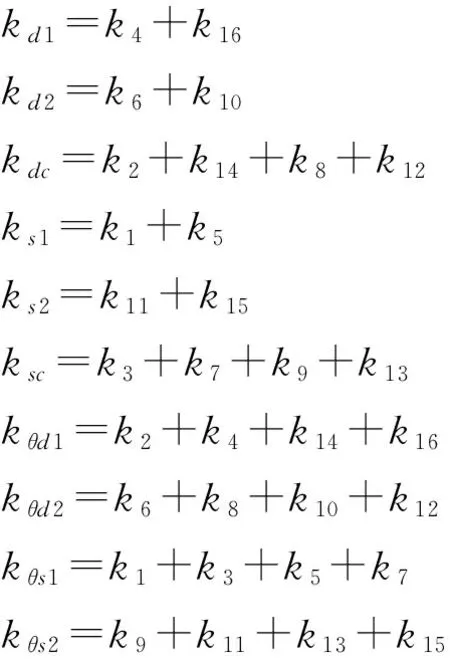
(6)

对式(5)作拉普拉斯变换，得到：

(7)

其中：

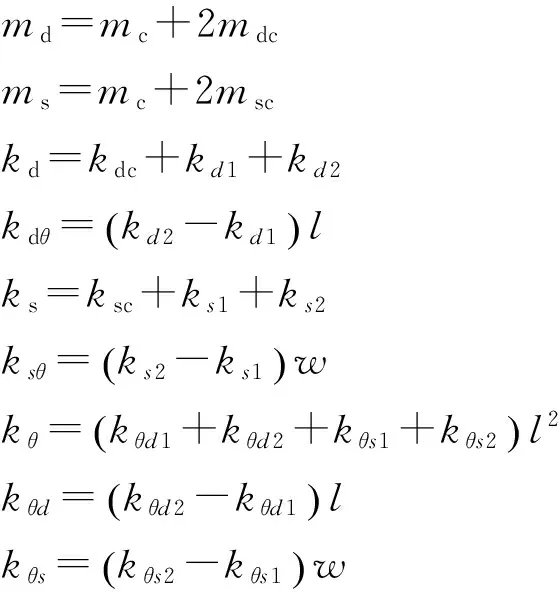
(8)

对式(7)做如下分析：

(1)在加工误差为0，所有驱动梁刚度相等、所有检测梁刚度相等的理想条件下，当敏感轴无角速度输入时，敏感结构驱动、检测和转动3个运动自由度相互间的耦合刚度系数均为0，因此敏感结构平面运动的3个自由度之间完全解耦。在陀螺作驱动运动时，不会产生检测运动和转动。

(2)当存在加工误差，使不同的驱动梁或检测梁之间刚度不相等时，陀螺3个方向上的运动发生相互耦合。根据式(7)，从驱动到检测的耦合直观上的作用途径是：驱动运动通过驱动-转动耦合刚度kθd使结构发生转动，再通过转动-检测耦合刚度ksθ使结构在检测方向发生运动。再由式(8)和式(6)，驱动-转动耦合刚度取决于结构上方和下方两组驱动梁刚度之差，即梁6、8、10、12刚度之和减去2、4、14、16刚度之和；转动-检测耦合刚度取决于单质量结构左方和右方两组外检测梁刚度之差，即梁11、15刚度之和减去梁1、5刚度之和。

3.3刚度耦合模型

考虑在驱动轴施加驱动力，检测轴不施加力，即Fs=0条件下驱动轴、检测轴和转动轴的运动。根据式(7)可写出从驱动力Fd到这3个位移的传递函数。表达式较为复杂，但如果耦合刚度与主刚度比是高阶小量，即kθdkdθ≪kdkθ、kθskds≪kskθ(由式(6)和(8)，这个条件很容易满足)，近似有驱动轴传递函数：

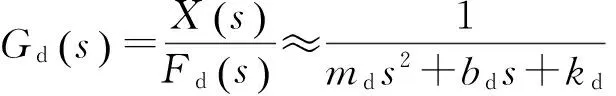
(9)

驱动-转动耦合传递函数：

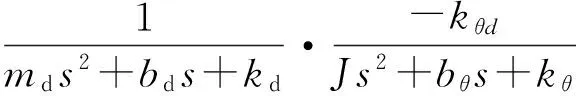
(10)

驱动-检测耦合传递函数：

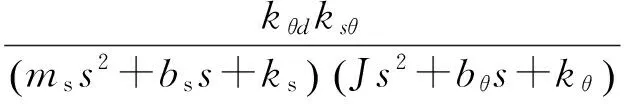
(11)

检测轴和驱动轴结构相同，有：

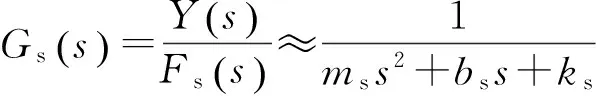
(12)

以上推导是从单边敏感结构得出的，整个陀螺的振动特性是两边结构振动特性的叠加，形式上如式(9)～(12)。

3.4耦合刚度辨识方法

实验测试得到的陀螺的频率响应特性包括了驱动电压到驱动力和位移到检测信号之间的增益。其中驱动电压到驱动力之间的增益可以通过测量实际结构参数和理论计算得到较准确的值，而位移到检测信号之间的增益不能用直接测量的方法得到其精确数值。但是即使如此，通过分析各种振动特性之间的关系，还是能够找到辨识陀螺梁结构刚度误差的方法。

分别用gdf和gdc表示驱动轴驱动电压到驱动力、位移到电压信号之间的增益；以gsf和gsc表示检测轴驱动电压到驱动力、位移到电压信号之间的增益，则实测驱动轴、检测轴、驱动-转动耦合、驱动-检测耦合的振动特性应分别为：

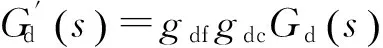
(13)

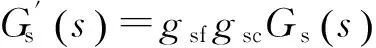
(14)

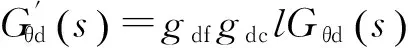
(15)

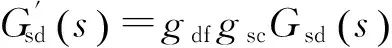
(16)

A驱动-转动耦合刚度系数辨识：

式(15)除以式(13)，有：

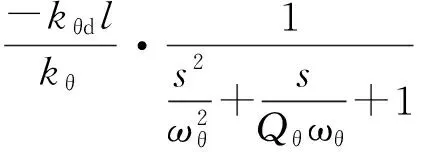
(17)

其中：ωθ和Qθ分别为转动模态的自然角频率和品质因数。根据式(8)，有：

(18)

其中：kθd1为上边4根驱动梁刚度之和，kθd2、kθs1和kθs2与之类似，分别对应于下边4根驱动梁、左边4根检测梁和右边4根检测梁。此处定义了刚度不对称系数α。

通过驱动-转动耦合特性与驱动轴频率特性的比值可以计算上边4根驱动梁总刚度与下边4根驱动梁总刚度的相对误差。

B转动-检测耦合刚度系数辨识：

式(16)除以式(14)，有：

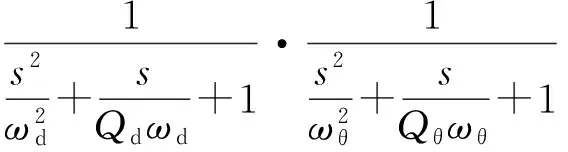
(19)

其中：ωd和Qd分别为驱动模态的自然角频率和品质因数。gdf和gsf可以根据结构参数计算得到，kθd/kθ由步骤A得到，则再根据实测的驱动轴和转动轴频率特性，可以计算得到ksθ/kd。由式(6)和(8)得：

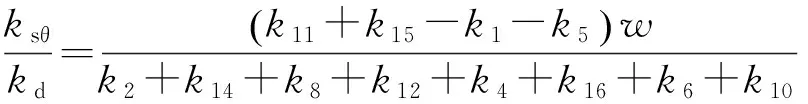
(20)

转动-检测耦合刚度ksθ取决于质量块右边外侧与左边外侧检测梁刚度的差。此处定义了刚度不对称系数β。

根据A的结果，可以用激光修调或其他方法调整上边或下边两组驱动梁的厚度就可以使驱动-转动耦合刚度接近于0，驱动-转动耦合运动会大为削弱；根据B的结果，修调右边外侧或左边外侧的检测梁，可以使转动-检测耦合刚度接近于0，转动-检测耦合运动被削弱。根据式(11)，这样可以使陀螺工作状态下的驱动-检测刚度耦合被双重削弱。

4　实验与结果

4.1实验方法

图6所示为实验装置，包括信号源、陀螺前置放大电路、模拟信号放大电路和真空系统，另外有计算机和扫频卡完成扫频和数据记录。扫频试验的方法为分别在驱动和检测轴施加频率连续变化的正弦驱动电压、分别在驱动和检测轴检测信号，获得陀螺的各种振动特性。

图6　实验装置

参考图1，每个质量块的上面和下面都有驱动检测梳齿，可分别检测质量块上端和下端的位移，上下两端位移的平均值为驱动轴位移信号，上下两端位移之差除以2l则为转动信号。这样得到陀螺驱动轴、检测轴、驱动-转动耦合和驱动-检测耦合振动特性。

除了在大气压下做测试外，还利用真空系统在100 Pa气压下进行了测试。常规的敏感结构批量测试是在大气压下进行的，因此以下使用大气压下的频率响应特性数据计算陀螺的耦合刚度。

4.2实验数据

图7所示为大气压下陀螺驱动轴和检测轴频率响应特性曲线，图8所示为陀螺驱动-检测耦合和驱动-转动耦合响应特性曲线。

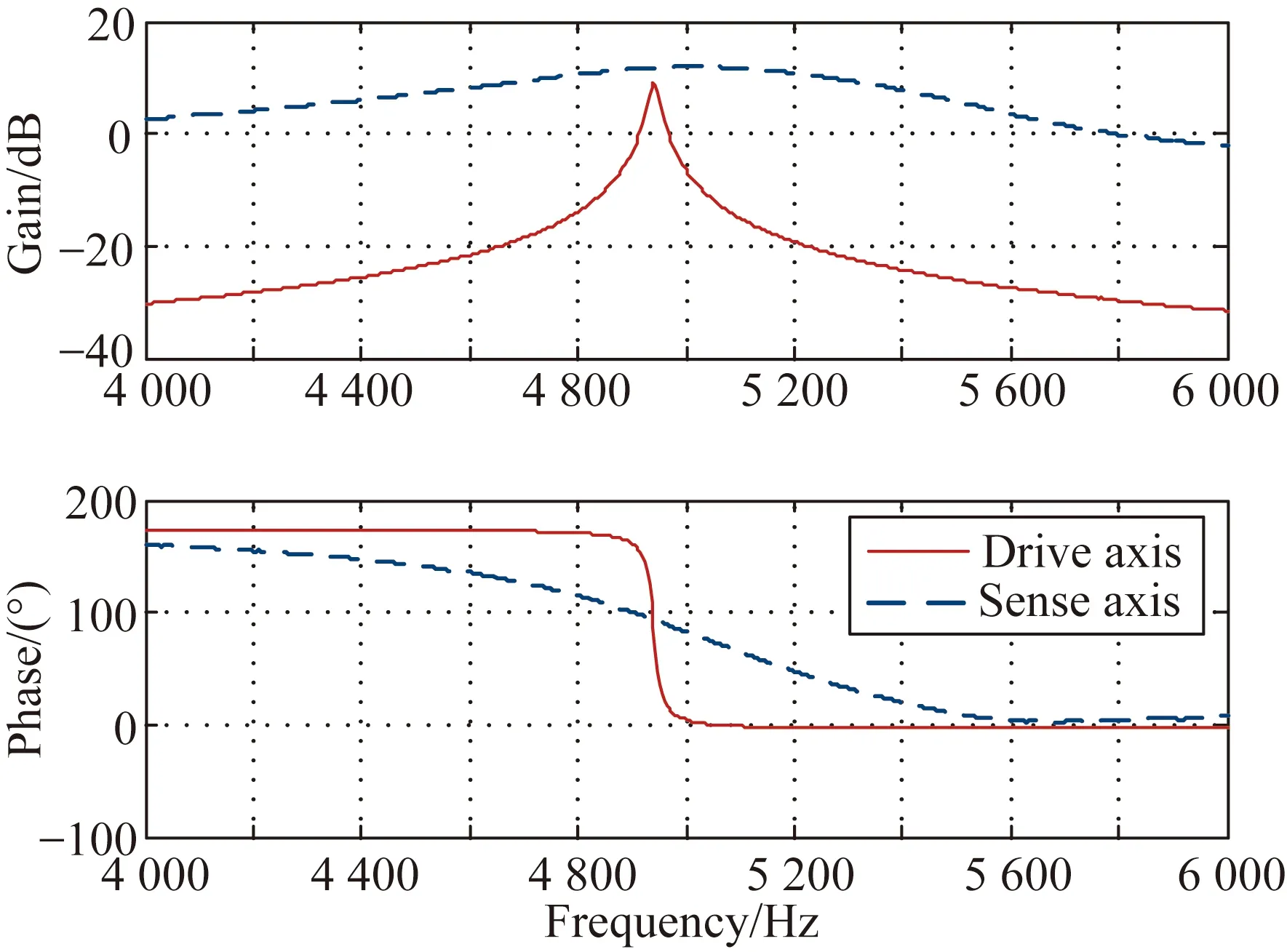
图7　驱动轴和检测轴频率响应(大气压)

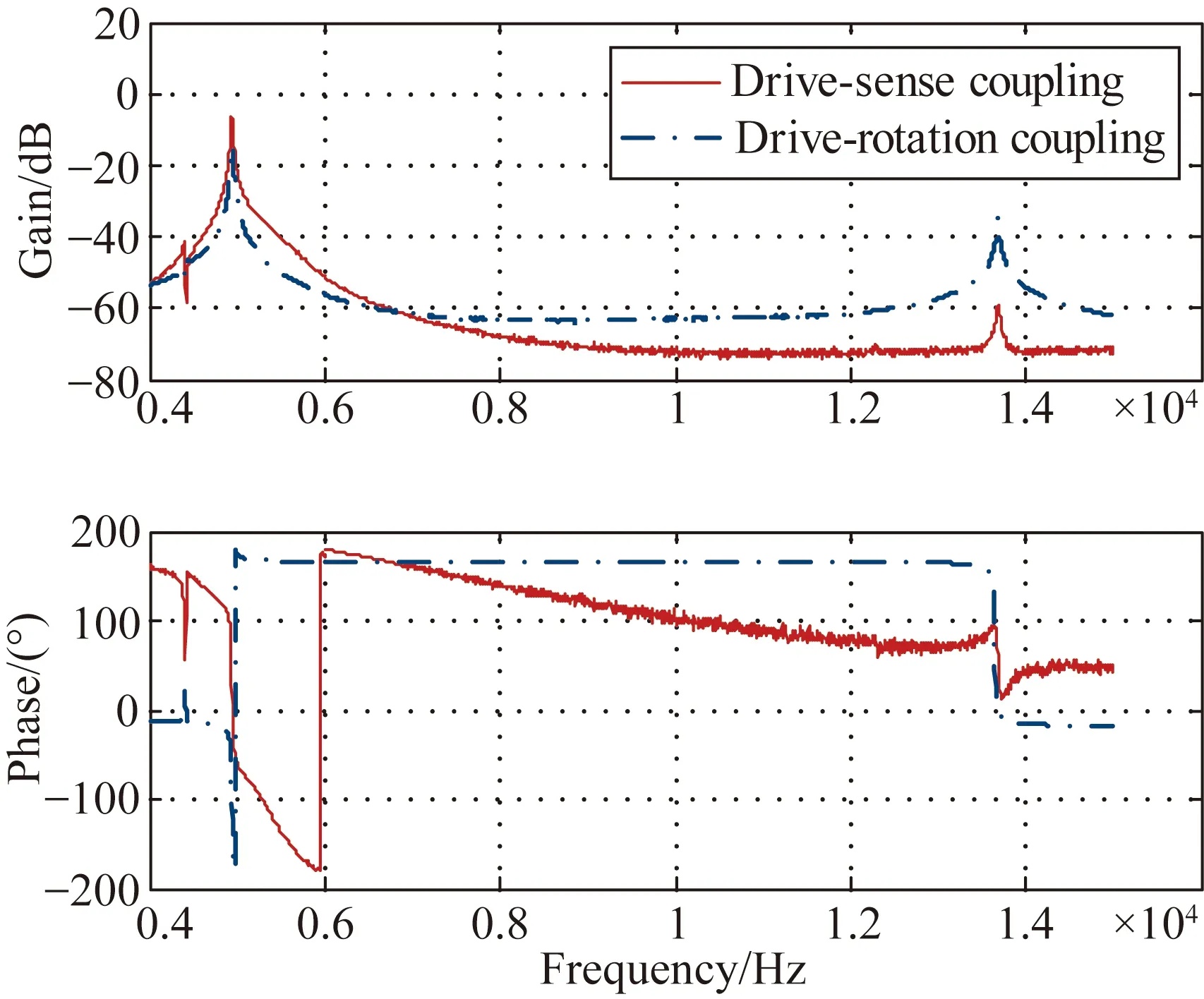
图8　驱动-检测耦合与驱动-转动耦合频率响应

得到参数如表3所示：

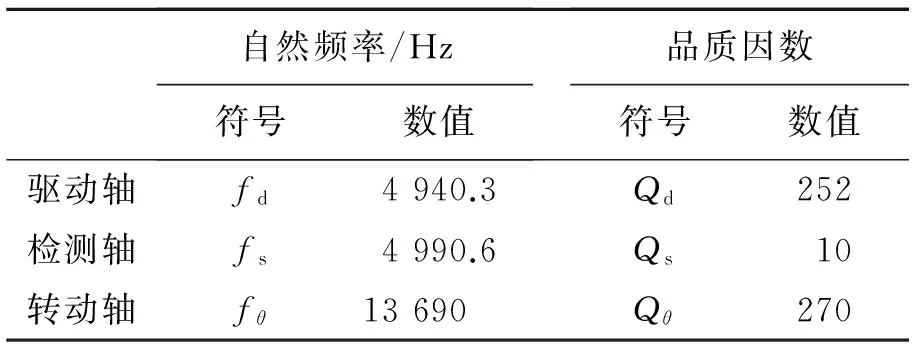
表3　振动自然频率和品质因数

其中驱动轴、检测轴自然频率4 940.3 Hz和4 990.6 Hz分别对应于仿真结果表2中的5 108 Hz 和5 163.2 Hz。由于对梁宽加工误差的估计不完全准确，造成仿真值和实测值之间有大约170 Hz的误差；但是仿真和实测的驱动轴和检测轴频率之差分别为50.3 Hz和55.2 Hz，误差仅为5 Hz。

由测试数据，在驱动轴自然频率fd处，驱动轴、驱动-转动耦合和驱动-检测耦合的增益分别为8.185 dB、-14.38 dB和-6.551 dB。

4.3耦合刚度辨识结果

由结构设计参数、梳齿间隙的实测值及驱动轴和转动轴自然频率的实测值可以计算得到gdf=14.27 μN/V，gsf=9.37 μN/V，kθ=2.357×10-3N·m，kd=578.0 N·m。根据式(17)～(20)和以上测试数据计算可得：

kθd/kθ=59.39 m-1，ksθ/kd=9.399×10-5m.

刚度不对称系数α=6.474×10-2，β=0.127 0；

驱动-转动耦合刚度系数kθd=0.140 0 N；

转动-检测耦合刚度系数ksθ=0.054 33 N。

5　结　论

本文提出了一种驱动与检测位移双向解耦的双质量微机电陀螺敏感结构形式，用仿真计算的方法分析了它的振动模态，完成了结构设计和加工。采用简化的梁的刚度特性，建立了微陀螺平面运动动力学方程，导出了结构的刚度耦合模型，确定了耦合刚度与梁的刚度误差的关系。提出了以驱动轴、检测轴、驱动-转动耦合和驱动-检测耦合频率响应特性为基础的耦合刚度辨识方法，通过驱动-转动耦合与驱动轴幅频特性之比可以辨识出驱动-转动耦合刚度系数，通过驱动-检测耦合与检测轴幅频特性之比可以辨识出转动-检测耦合刚度系数。耦合刚度辨识方法把耦合刚度产生的根源定位到特定的几组梁之间的刚度误差。实验测试了微陀螺的频率响应特性，完成了对驱动-转动和转动-检测耦合刚度系数的辨识，所测试陀螺的驱动-转动和转动-检测耦合刚度系数分别为0.14 N和0.054 33 N。辨识结果可用于对梁的刚度的激光修调或静电调整。

[1]赵阳， 裘安萍， 施芹， 等. 硅微陀螺仪零偏稳定性的优化[J]. 光学 精密工程， 2014， 22(9): 2381-2388.ZHAO Y， QIU A P， SHI Q，etal.. Optimization of bias stability for silicon microgyroscope [J].Opt.PrecisionEng.， 2014， 22(9): 2381-2388. (in Chinese)

[2]陈志勇， 张嵘， 周斌. 一种低机械噪声弱耦合的微机电陀螺敏感结构[J]. 中国惯性技术学报， 2015， 23(3): 373-378.

CHEN ZH Y， ZHANG R， ZHOU B. MEMS gyroscope structure with low mechanical-thermal noise and weak mechanical coupling [J].JournalofChineseInertialTechnology， 2015， 23(3): 373-378. (in Chinese)

[3]XIE J B， YUAN W ZH， CHANG H L. Design and fabrication of MEMS gyroscopes on the silicon-on-insulator substrate with decoupled oscillation modes[J]. Chinese Journal of Mechanical Engineering， 2010， 23(1):16-20.

[4]SONMEZOGLU S， TAHERI-TEHRANI P， VALZASINA C，etal.. Single-Structure Micromachined Three-Axis Gyroscope With Reduced Drive-Force Coupling[J].ElectronDeviceLetters，IEEE， 2015， 36(9): 953-956.

[5]DING H T， LIU X S， LIN L T，etal.. A high-resolution silicon-on-glass axis gyroscope operating at atmospheric pressure[J].SensorsJournal，IEEE， 2010， 10(6): 1066-1074.

[6]周浩， 苏伟， 刘显学， 等. 解耦Z轴微机械陀螺的研制[J]. 光学 精密工程， 2011， 19(9): 2123-2130.ZHOU H， SU W， LIU X X，etal.. Development of decoupledz-axis micromachined gyroscope [J].Opt.PrecisionEng.， 2011， 19(9) : 2123-2130. (in Chinese)

[7]姜劭栋， 裘安萍， 施芹， 等. 硅微陀螺仪正交耦合系数的计算及验证[J]. 光学 精密工程， 2013， 21(1): 87-93.

JIANG SH D， QIU A P， SHI Q，etal.. Calculation and verification of quadrature coupling coefficients of silicon microgyroscope [J].Opt.PrecisionEng.， 2013， 21(1): 87-93. (in Chinese)

[8]孙香政， 王刚， 郭志想， 等. 耦合结构对音叉式陀螺振动特性的影响[J]. 传感技术学报， 2013， 26(12): 1695-1699.

SUN X ZH， WANG G， GUO ZH X，etal.. Influence of coupled mechanism on vibration characteristics of tuning fork gyroscope [J].ChineseJournalofSensorsandActuators， 2013， 26(12): 1695-1699.(in Chinese)

[9]贺琨， 崔红娟， 侯占强， 等. 微机械振动陀螺模态耦合误差分析与激光修形方法研究[J]. 传感器与微系统， 2013， 32(3): 21-24.

HE K，CUI H J，HOU ZH Q，etal.. Study on modal coupling error analysis and laser trimming method for micromachining vibration gyroscope [J].TransducerandMicrosystemTechnologies， 2013， 32(3): 21-24. (in Chinese)

[10]倪云舫， 李宏生， 杨波， 等. 硅微陀螺正交误差直流校正设计与分析[J]. 中国惯性技术学报， 2014，22(1):104-108.

NI Y F， LI H SH， YANG B，etal.. Design and analysis of a quadrature correction method using DC voltages for silicon micro-gyroscope [J].JournalofChineseInertialTechnology， 2014，22(1):104-108. (in Chinese)

[11]SU JB， XIAO D B， WU X ZH，etal.. Improvement of bias stability for a micromachined gyroscope based on dynamic electrical balancing of coupling stiffness [J].J.Micro/Nanolith.MEMSMOEMS.， 2013， 12(3):033008.

[12]CAO H L， LI H SH， KOU ZH W，etal.. Optimization and experimentation of dual-mass MEMS gyroscope quadrature error correction methods [J].Sensors， 2016， 16(1): 71.

陈志勇(1973-)，男，河北石家庄人，博士，副研究员。1996年、2001年于清华大学分别获得学士、博士学位，主要从事微机电惯性器件方面的研究。E-mail: chendelta@tsinghua.edu.cn

刘悦琛(1990-)，女，天津人，硕士研究生。2013年于清华大学获得学士学位，主要从事微机电惯性器件方面研究。E-mail：1098553453@qq.com

(版权所有未经许可不得转载)

Identification of coupling stiffness for MEMS gyroscope

CHEN Zhi-yong*， LIU Yue-chen， ZHANG Rong， ZHOU Bin

(DepartmentofPrecisionInstrument，TsinghuaUniversity，Beijing100084，China)*Correspondingauthor，E-mail：chendelta@tsinghua.edu.cn

For identification of the coupling stiffness of MEMS (Micro-electro-mechanical System) gyroscopes， a identification method was proposed based on the frequency response characteristics of the drive-axis， sense axis， drive-to-rotation coupling and rotation-to-sense coupling. A dual-mass linear vibrating MEMS gyroscope with decoupled drive-to-sense and sense-to-drive displacement was designed. Based on simplified stiffness characteristics of the beams， the dynamic planar movement equations of the gyroscope were established and the drive-axis， sense-axis， drive-to-rotation and drive-to-sense transfer functions were derived. According to the coupling model， the sources of stiffness coupling were attributed to the stiffness error of specific beams. The drive-to-rotation coupling stiffness could be identified by the ratio of drive-to-rotation coupling to drive-axis frequency responses， and rotation-to-sense coupling stiffness could be identified by the ratio of drive-to-sense to sense-axis frequency responses. The frequency responses of the gyroscope were investigated by the proposed coupling stiffness identification method， and results show that coupling stiffness coefficients by drive-to-rotation and rotation-to-sense for the tested gyroscope are 0.14 N and 0.054 33 N， respectively. It concludes that the identification results provide

for laser trimming of the beams for gyroscopes.

MEMS gyroscope; coupling stiffness; identification method; model; frequency response

2016-04-12；

2016-05-17.

武器装备预先研究资金资助项目(No.51309010303)

1004-924X(2016)09-2240-08

V241.5

A

10.3788/OPE.20162409.2240