机器视觉精密测量中的显微光学聚焦
徐 征,陈聿夫,孙 谦,王晓东,周宗磊
(大连理工大学 微纳米技术及系统辽宁省重点实验室,辽宁 大连 116085)
机器视觉精密测量中的显微光学聚焦
徐征,陈聿夫,孙谦,王晓东*,周宗磊
(大连理工大学 微纳米技术及系统辽宁省重点实验室,辽宁 大连 116085)
考虑显微光学涉及的聚焦精度对机器视觉精密测量效果的影响,开展了显微视觉环境下对图像聚焦技术综合定量评价的研究。建立了偏移率等系列性能指标,对13组清晰度函数在显微视觉条件下的无偏性、单峰性、分辨力等进行了综合评价,优选出方差函数和Brenner函数分别用于粗聚焦和精聚焦阶段的清晰度计算。建立了分步爬山搜索法,实现了显微自动聚焦。与传统爬山法相比,提出的方法聚焦时间显著缩短,重复精度提高约24%。将建立的自动聚焦与图像测量方法应用于某电液伺服阀衔铁气隙测量中,得到的测量均值与工具显微镜结果相近,而测量标准差可达1.9 μm,测量效率也显著提高。最后对伺服阀加电条件下的气隙动力学特性进行了测试,获得了驱动电流-衔铁气隙之间的关系,为在线装配/装调提供了重要依据。
机器视觉;显微成像;自动聚焦;微装配;微机电系统;综合定量评价
1 引 言
现代工业的快速发展对微传感器和微执行器的综合性能提出了更高要求。目前,许多微传感器和微执行器的精密装调工作仍依靠手工操作,导致装配精度差和应力分布波动大等问题,影响了它们的服役稳定性。以显微视觉为导引,通过精密定位和微小夹持装置将多个微零件精确组装成系统的微装配技术是解决上述问题的主要途径,而在装配-装调之前,基于显微视觉的在线测量是不可或缺的环节[1-3]。在短景深的显微视觉下,光学聚焦对测量效果的影响显著,离焦偏差会使精密工具误动作,从而导致工具或零件的损坏等问题[4]。此外,受表面涂胶等工艺的影响,留给光学聚焦的时间窗很窄,手工聚焦难以满足需求,亟待发展高效自动的显微光学聚焦技术。
显微自动聚焦技术通常基于图像,要解决图像清晰度计算和合焦面搜索两个问题[5-6]。国内外学者对此开展了大量研究。Li等以直径为10 μm 左右的轴-孔装配为应用对象,基于Sobel算子设计了先聚焦整体孔、再聚焦中心区的两步搜索法,使注射针尖移动到合焦面,误差小于0.5 μm[7]。Liu等设计了一种组合算法,先采用方差函数对微执行器整体聚焦,再以四叉树算法聚焦微执行器的尖端[8]。Qiu等提出以Krisch边缘算子卷积和评价粗聚焦清晰度、以图像高频成分比评价精聚焦清晰度的双重算法,准确度达到±4 μm[9]。Bilen等以方差函数计算清晰度,选择Fibonacci法作为搜索策略对微夹钳聚焦,1倍镜头下的定位准确度可达2.7 μm[10]。
上述研究主要是将图像聚焦技术作为不同应用的中间环节,缺乏对该技术在显微视觉环境下的综合定量评价。本文建立了偏移率等系列性能指标,对13组清晰度计算函数在显微视觉条件下的无偏性、单峰性、分辨力进行定量评价,选出适用于粗/精聚焦的清晰度函数,并建立分步爬山搜索策略,实现显微自动聚焦。以精密电液伺服阀衔铁气隙为对象,利用测距传感器验证聚焦搜索的重复性。最后,实现了衔铁气隙动力学特性的自动测量,获得了驱动电流-衔铁气隙之间的关系,为其装配/装调提供可靠依据。
2 实验装置组成
本文所用的实验装置是为某企业开发的精密微装调设备的一部分。如图1所示,实验装置包括传送微组件的2维精密滑台(Y向和Z向滑台,分辨力为2 μm)、用于聚焦的精密直线滑台(X向滑台,分辨力为2 μm)、显微镜(Navitar,2.0×)、摄像机(DH-SV2001,单像素为4.4 μm×4.4 μm)和环形光源组成。为了对比聚焦精度,在显微成像单元旁加装有激光测距位移传感器(ZX2-LD50L,分辨力为1.5 μm)。
测试对象为某精密电液伺服阀的衔铁区域(12 mm×4 mm)。如图2所示,衔铁与基体间的气隙(0.34 mm)是决定流体控制精度的关键,对性能影响显著。实际生产中,需要根据气隙偏差进行衔铁或垫片更换及紧定螺钉调节等装调作业,使静态气隙更为均匀、加电时气隙变化线性度更高。

图1 显微视觉单元的结构组成

图2 待测的伺服阀及其衔铁气隙结构
系统的工作过程如下:首先由传送滑台将伺服阀组件传送到操作区,再采集衔铁区的图像,并计算图像清晰度,驱动滑台搜索物面,待聚焦准确后测量微小特征,最后根据测量结果对组件进行装配和装调。
3 清晰度函数评价及搜索策略
3.1清晰度计算函数
本文采用梯度算子类函数、统计函数和图像熵函数3类函数计算清晰度,并通过对比这3种函数的性能选出最佳函数。
(1)梯度算子类函数:Roberts算子及衍生函数(FRoberts、FRob-Energy)、Sobel算子及衍生函数(FSobel、FTenengrad、FSML)、Prewitt算子函数FPrewitt、梯度绝对值函数FSMD、梯度平方和函数FEOG、Laplace算子函数FLaplace以及Brenner算子函数FBrenner。
(2)统计函数:方差函数FVariance和自相关函数FVollaths。
(3)图像熵函数FEntropy。合焦图像与离焦图像之比,熵函数多样性大,即信息熵高。
3.2清晰度函数的特征参量
为了评价函数的聚焦特性,采用近焦区宽度Wclose和拐点到合焦点距DI-to-F为设计参量。首先引入近焦区与远焦区的概念。如图3所示,以FTenengrad为例,函数顶点处为合焦点。合焦点附近为近焦区,成像相对清晰,曲线陡峭。将成像模糊、曲线平缓的区域称为远焦区。远焦区函数曲线可近似为与位置坐标轴平行的线段:

(1)Fi是在第i个图像采样位置处的函数归一化计算值。临界点(Xn,Fn)到该线段的距离d=|Fn-b|,Fn为临界点处图像清晰度的计算值,Xn即为临界点采样位置。当满足d>α,α为阈值(取0.001),同样,从右到左可以获取右临界点的坐标。左、右临界点的距离Wclose=|XR-XL|为近焦区宽度,XL,XR分别为左、右临界点的采样位置。粗聚焦步长应小于函数近焦区宽度。


图3 Tenengrad函数特征分析
3.3清晰度函数的性能评价指标
在各清晰度函数的近焦区,函数的综合性能指标评价设计如下:
(1)表达函数无偏性的最值点偏移率:

(2)
其中:Xmax为函数取最大值的点,X0为真实聚焦清晰点,δ为相邻采样点的物理间距,Wdof为镜头的景深(~20 μm)。偏移量反映函数是否满足无偏性,若Roffset>1,则不满足无偏性。
(2)函数清晰度比率为计算值变化的比值:
Ra=Fmax/Fmin,
(3)
其中Fmax,Fmin分别为函数的最大值和最小值。
(3)综合衡量合焦点附近陡峭程度的参量为:
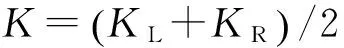
(4)
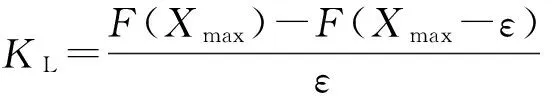

(4)以局部极大值点个数Np衡量抗干扰能力和单调性。在近焦区内的局部极值点越少,搜索落入局部极值的可能性越小。
(5)清晰度的计算时间Tc。
3.4分步爬山法
为消除导轨回程误差对聚焦精度的影响,本文改进了传统爬山法,在清晰度函数2个特征参量的基础上,建立了分步爬山法,减少往复搜索次数,搜索过程如图4所示。搜索步骤如下:
(1)在粗聚焦阶段,以大步长Sc(Sc (2)以步长S1搜索清晰度函数的右临界点。由临界点计算公式,定义阈值因子: ρ=d/b, (5) d,b的定义见式(1)。记录两相邻采样点的函数值F1和F2,计算相对变化率: r′=r/F1, (6) (7) 其中δ为相邻采样点的间距。当r′>ρ,缩小步长,否则继续搜索。 图4 改进的分步爬山搜索法流程 (4)根据F函数值,以步长S3搜索合焦点,找到聚焦清晰平面所在的小区域,反向移动一个合焦点偏差估计距离。 4.1聚焦清晰度函数的综合性能 图5 各函数计算的图像序列清晰度 利用3.3节中的评价指标对13组清晰度函数的计算结果(图5)进行分析(表1),结论如下: (1)FVariance近焦区的宽度Wclose最大,为720 μm,其次是FTenengrad的Wclose为408 μm,其余函数的Wclose均远小于方差函数。计算各函数的DI-to-F,除FVariance外,其余DI-to-F均在40~72 μm。FVariance在近焦区波动较大,而且没有明显的拐点。 (2)FVariance的无偏性Roffset为2.4,不满足无偏性。此外,FLaplace和FPrewitt的Roffset是0.8,偏移量较大。其余均满足无偏性。 (3)FTenengrad和FBrenner的清晰度比率较高,分别为10.06和9.43。 (4)FSML,FTenengrad,FRob-Energy,FBrenner,FEOG函数的陡峭度超过0.022,这意味着在精聚焦阶段搜索过程中,其合焦面更易分辨。 (5)除FVariance外,各函数在近焦区均严格满足单调性。但FEntropy,FLaplace,FSML等在各自的远焦区不是严格单调递增的。 (6)FEOG,FRob-Energy,FTenengrad函数的计算时间分别为42,43,46 ms,其它函数的计算时间不超过32 ms,原因是这3个函数的平方运算多,计算复杂度高。 综上,方差函数的近焦区较宽,可设置较大的粗聚焦搜索步长,减少采样次数,但无偏性较差,仅适合在粗聚焦阶段使用。对精聚焦而言,FTenengrad函数的无偏性、清晰度比率、单调性等均理想,但耗时较长;而FBrenner与FTenengrad的性能接近,因此选择FBrenner函数在精聚焦阶段计算清晰度。 表1 清晰度评价指标的计算结果 4.2聚焦搜索策略对比实验 按图4流程进行衔铁气隙聚焦实验。总搜索范围约为8 mm,以方差函数计算粗聚焦阶段的清晰度,步长Sc取为640 μm。在精聚焦阶段,以Brenner函数和Tenengrad函数计算清晰度并进行比较,近焦区搜索步长S1约为Wclose/4;拐点搜索步S2 用测距传感器测量传感器到激光反射物面的距离,记录聚焦位置到反射面的距离li,每组聚焦20次,以聚焦测量结果的标准差S衡量重复性(表2)。其中Tf为所耗费的时间。 表2 自动聚焦实验结果 与传统爬山法相比,分步爬山法往复运动次数少,从而抑制了滑台回程误差的影响,聚焦重复精度为4 μm,为镜头景深的1/5,重复精度提高约24%;同时缩短了聚焦时间。此外,Tenengrad函数的聚焦准确度相对更高,而Brenner函数的聚焦效率更高,也间接验证了4.1节函数性能的分析结果。 4.3伺服阀气隙的测试实验 静态气隙尺寸测量的具体过程为:以上述算法对衔铁和基体分别聚焦,提取两者边缘,其中一条边缘以最小二乘法拟合直线,另一条边缘等间隔取点计算到该直线的平均距离,再将其换算为实际气隙值gi。用工具显微镜(STM6-F10)对同一气隙测量多点求平均,并与gi进行对比。分析10组测量数据发现:本方法的测量值为358.8~365.1 μm,标准差为1.9 μm;而工具显微镜的测量值为352.2~368.4 μm,标准差为5.37 μm。二者均值的相对偏差为0.36%。本文中聚焦和测量均为自动化操作,测量一次耗时约40 s,而用工具显微镜则要手工对焦和取样,耗时约2 min。 图6 加电过程中伺服阀气隙变化 加电状态气隙变化线性度是伺服阀的另一重要指标,本文结合上述算法测量加电(分辨率为1 mA)状态下的气隙变化,通过模板匹配法获取变化量。由图6可知,当电流为0时左气隙比右气隙大将近226 μm。加电过程中气隙变化可分为3段,左右变化率也不相等。在区段2,左右两侧气隙随电流变化率的绝对值分别为25.2 μm/mA和25.7 μm/mA,气隙位移变化明显;在区段1,左右气隙的变化率分别为2.8 μm/mA和2.6 μm/mA;而区段3的变化率分别为1.5 μm/mA和。上述结果为微装配/装调提供了实验依据。 本文建立了偏移率等系列性能指标,对多种清晰度计算函数在显微视觉条件下的无偏性、单峰性和分辨力进行了综合评价。其中,方差函数的近焦区域较宽,搜索步长较大,但无偏性较差,适合在粗聚焦阶段使用;而Tenengrad函数的无偏性、清晰度分辨力、单调性等性能均较理想,但计算时间偏长;Brenner函数的性能与Tenengrad函数接近,并且计算时间适中,适合在精聚焦阶段计算清晰度。 在传统爬山法的基础上,结合清晰度函数的特征参量建立了分步爬山法。该方法减少了往复搜索次数,消除了滑台回程误差对聚焦精度的影响,提高了聚焦的重复性和效率。 利用自动聚焦算法测量伺服阀气隙,并与工具显微镜的测量结果对比,相对偏差为0.36%,能满足测量精度要求,而且显著改善了测量效率。 [1]YE X, GAO J, ZHANG Z J,etal.. Robotic microassembly for meso-scale application [J].IndustrialRobot:AnInternationalJournal, 2015, 42(2): 142-148. [2]WASON J D, WEN J T, GORMAN J J,etal.. Automated multiprobe microassembly using vision feedback [J].IEEETransactionsonRobotics, 2012, 28(5): 1090-1103. [3]娄志峰,王晓东,由博,等. 精密微小组件压装技术及仪器[J]. 光学 精密工程,2015,23(6):1605-1611. LOU ZH F, WANG X D, YOU B,etal.. Pressing-fitting technology and instrument for precision small parts [J].Opt.PrecisionEng., 2015,23(6):1605-1611.(in Chinese) [4]唐永龙,张之敬,张晓峰,等. 微装配正交精确对准系统的设计[J]. 光学 精密工程,2012,20(7): 1542-1550. TANG Y L, ZHANG ZH J, ZHANG X F,etal.. Design of precise alignment orthogonal system used in micro-assembly [J].Opt.PrecisionEng., 2012,20(7):1542-1550.(in Chinese) [5]周丽平,孙志峻,张泉. 显微视觉系统的自动聚焦及控制[J]. 光学 精密工程,2013,21(3):807-812.ZHOU L P, SUN ZH J, ZHANG Q. Auto-focusing and control of micro-vision system [J].Opt.PrecisionEng., 2013,21(3): 807-812.(in Chinese) [6]MAIER A, NIEDERBRUCKER G, STENGER S,etal.. Efficient focus assessment for a computer vision-based Vickers hardness measurement system[J].SPFE, 2011, 8000(17):477-526. [7]LI F D, XU D, SHI Y L,etal.. Motion-based microscopic camera calibration and application on micro tube-hole insertion [J].OpticalEngineering, 2014, 53(5): 53103-53109. [8]LIU J, GONG Z, TANG K,etal.. Locating end-effector tips in robotic micromanipulation [J].IEEETransactionsonRobotics, 2014, 30(1): 125-130. [9]QIU Y R, LI Y H, CHEN Y X,etal.. Experiments on image processing for micro-assembly [J].AppliedMechanicsandMaterials, 2013, 333-335(1): 924-928. [10]BILEN H, HOCAOGLU M A, UNEL M,etal.. Developing robust vision modules for microsystems applications [J].MachineVisionandApplications, 2012, 23(1): 25-42. 王晓东(1967-),男,黑龙江哈尔滨人,教授,1989年于南京航空学院获得学士学位,1992年于哈尔滨船舶工程学院获得硕士学位,1995年于哈尔滨工业大学获得博士学位,主要从事微装配技术与系统、精密仪器等方面的研究。E-mail:xdwang@dlut.edu.cn (版权所有未经许可不得转载) Auto-focusing in optical microscopy for machine-vision-based precise measurement XU Zheng, CHEN Yu-fu, SUN Qian, WANG Xiao-dong*, ZHOU Zong-lei(KeyLaboratoryforMicro/NanoTechnologyandSystemofLiaoningProvince,DalianUniversityofTechnology,Dalian116085,China)*Correspondingauthor,E-mail:xdwang@dlut.edu.cn The auto-focusing precision of microscopy has great influence on the performance of machine-vision-based precise measurement. A comprehensively quantitative evaluation method on image auto-focusing technique in a microscopic vision environment was researched. Several kinds of evaluation indexes were proposed, and the unbiasedness, unimodality, spatial resolutionetc. of 13 groups sharpness functions were comprehensively evaluated in a microscopic vision condition. Then variance function and Brenner function were chosen to calculate the sharpness functions in coarse and fine focusing processes respectively. A modified Mountain Climbing Searching (MCS) algorithm was proposed to implement the micro-automatic focusing. As comparing to common MCS method, the modified method significantly improves the time consuming and increases the repeatability by about 24%. Finally, the developed auto-focusing algorithm was integrated into the system and was applied to the measurement of armature gap in a servo solenoid valve. The results show that the standard deviation of measurement is 1.9 μm, the precision is similar to that of the universal tool microscope, and the efficiency is significantly improved. Moreover, the system was also utilized for dynamic characteristic detection of gaps in the solenoid valve under the condition of power up, the relation between driving current and armature gap is obtained, which provides a reliable evidence for in-situ micro-assembly. machine vision; microscopic imaging; auto-focusing; microassembly; Micro-electro-mechanical System(MEMS); comprehensively quantitative evaluation 2016-03-01; 2016-04-19. 国家科技重大专项基金资助项目(No.2013ZX04001091) 1004-924X(2016)09-2095-06 TP242.6;TH742.9 A 10.3788/OPE.20162409.2095 徐征(1973-),男,河南郑州人,博士,副研究员,1997年、2000年于吉林工业大学分别获得学士和硕士学位,2004年于大连理工大学获得博士学位,主要从事微纳集成制造的研究。E-mail:xuzheng@dlut.edu.cn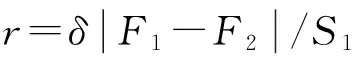
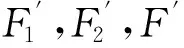

4 实验验证与分析
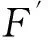

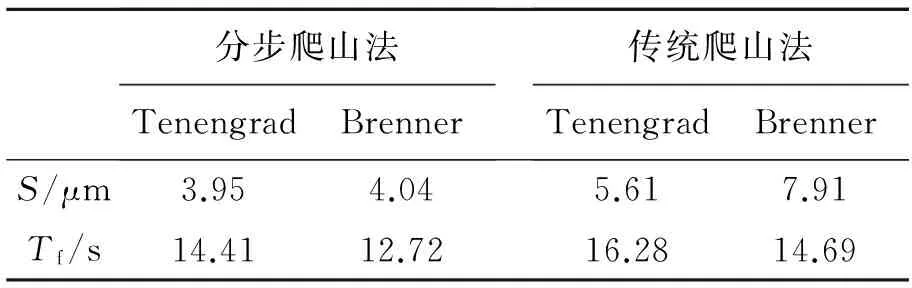

5 结 论



