利用求根MUSIC算法进行快速波达方向估计
王新贺,周 围,2
(1.重庆邮电大学移动通信技术重庆市重点实验室,重庆400065;2.重庆邮电大学光电工程学院,重庆400065)
利用求根MUSIC算法进行快速波达方向估计
王新贺1,周围1,2
(1.重庆邮电大学移动通信技术重庆市重点实验室,重庆400065;2.重庆邮电大学光电工程学院,重庆400065)
针对经典波达方向(direction of arrival,DoA)估计算法复杂度高的问题,讨论了2种快速估计DoA的算法,即:传播算子求根多重信号分类(multiple signal classification,MUSIC)算法与多级维纳滤波器求根MUSIC算法.传播算子求根MUSIC算法是对协方差矩阵分块,得到传播算子构建噪声子空间,结合求根MUSIC算法估计出DoA.多级维纳滤波器不需要估计协方差矩阵,通过滤波器的前向递推,求解维纳-霍夫方程,得到信号子空间,根据正交投影原理,计算出噪声子空间与其共轭转置的乘积,结合求根MUSIC算法估计出DoA.这2种算法都不需对协方差矩阵奇异值分解和谱峰搜索,通过数学分析,复杂度明显降低.
波达方向估计;多级维纳滤波器;传播算子;求根MUSIC算法
波达方向(direction of arrival,DoA)是空间谱估计研究中的一个热点.目前针对DoA估计有很多优良的算法,最经典的是基于子空间的多重信号分类(multiple signal classification,MUSIC)和通过旋转不变性技术估计信号参数(estimating signal parameters via rotational invariance techniques,ESPRIT)算法[1],这2种算法的估计精度高,但计算量非常大.MUSIC需要通过接收信号得到其协方差矩阵,利用子空间的正交性对协方差矩阵进行特征值或奇异值分解得到信号子空间和噪声子空间,再通过谱峰搜索得到相应的波达角度.ESPRIT算法需要将整个阵列划分成完全相同结构的子阵,同样也需要对阵列数据协方差矩阵进行特征分解.与MUSIC算法不同的是,ESPRIT利用子空间的旋转不变性对协方差矩阵进行特征值分解,并且,ESPRIT算法不需要谱峰搜索,利用各子阵信号子空间的旋转不变性求出信号的入射角信息.由于不需要谱峰搜索,相对于MUSIC算法,ESPRIT算法计算量要小.针对上述2种算法计算量大的问题,文献[2-3]提出了一种不需要对协方差矩阵特征值分解的传播算子算法;文献[4-5]提出了一种求根MUSIC算法,避免了谱峰搜索;文献[6-8]提出了一种利用参考信号来获取噪声子空间的方法;文献[9]针对上述方法的局限性,提出了一种不需要参考信号的方法;文献[10]提出了一种针对非圆信号的滤波器算法.本文讨论了2种快速估计DoA的算法,即传播算子求根MUSIC(PM root-MUSIC,PRM)算法和多级维纳滤波求根MUSIC(MSWF root-MUSIC,MRM)算法.
1 信号模型
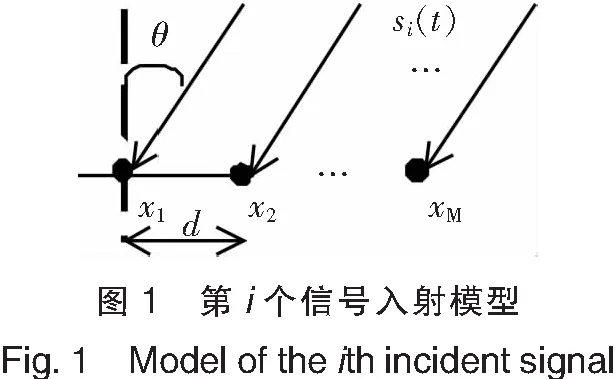
假设K个相互独立的波长为λ的窄带平面波入射到M个阵元的等距直线阵列上,阵元间隔为d,图1为信号入射模型.
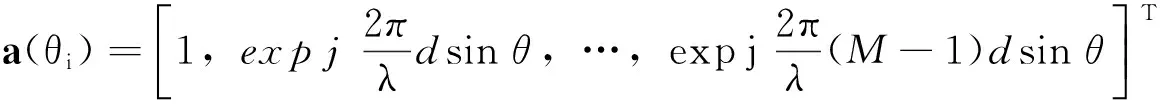
2 算法描述
2.1PRM算法
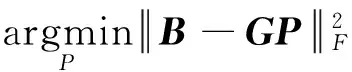
(1)
2.2MRM算法
MRM算法只需要知道期望信号的参考信号,通过多级维纳滤波器的前向递推不需要估计协方差矩阵和对其作特征值分解,就可以得到信号子空间,基于正交投影变换即可得出噪声子空间.
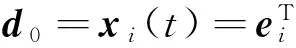
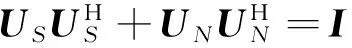
3 复杂度分析
经典的MUSIC算法,估计协方差矩阵所需要的运算量约为o(M2N),对其作特征值分解所需要的运算量约为o(M3),谱峰搜索的复杂度为o(MKL),它的总的复杂度为o(M2N)+o(M3)+o(MKL),其中:M是阵列的阵元个数;N是采样快拍数;K为信源数;L代表搜索精度,并且K 通过算法分析可知,PRM算法只需对阵列输出数据求取协方差矩阵R,并对其分块,求取传播算子,进而得到噪声子空间,再通过求根MUSIC算法得到波达角度.PRM算法不需要对协方差矩阵作特征值分解,在求传播算子过程中,矩阵求逆的复杂度为o(K3);也不需要谱峰搜索,它是以求根MUSIC算法来代替谱峰搜索,求根MUSIC算法的复杂度为o((2(M-1))3),PRM算法总的复杂度为o(K3)+o(M2N)+o((2(M-1))3),远远小于经典的MUSIC算法. 与PRM算法相比,MRM算法不需要估计协方差矩阵,通过多级维纳滤波器,在最小均方的意义下得到维纳-霍夫方程的最优解.在MSWF中,每一级匹配滤波器所需要的运算量是o(MN),本文讨论的MSWF是使用了J级维纳滤波器,因此估计噪声子空间的复杂度为o(MNJ),求根MUSIC算法的复杂度为o((2(M-1))3),MRM算法总的复杂度为o((2(M-1))3)+o(MNJ),K 为了验证PRM算法和MRM算法的性能,进行了仿真实验,仿真条件:阵列为各向同性的等距均匀直线阵,阵元数为7,阵元间距d=0.5λ,有3个独立的远场窄带信号入射到接收阵列,信号波达角度分别为0°,30°,60°. 实验1波达角度估计 仿真条件:假设信噪比SNR为10dB,快拍数为500,阵列接收的噪声为加性高斯白噪声,进行了100次MonteCarlo实验.图2是MRM算法和PRM算法在上述仿真条件下对波达角度的估计,并与实际角度的对比,仿真结果表明,这2种算法都能准确地估计出信源的DoA. 实验2不同信噪比下算法的性能 仿真条件:快拍数为200,SNR为-10~30dB,进行了100次MonteCarlo实验.图3是MRM算法和PRM算法在上述仿真条件下不同信噪比对应的成功概率.由仿真结果可以看出,随着信噪比的增大,MRM算法和PRM算法的成功概率逐渐向100%逼近,在信噪比为2dB时,2种算法的成功概率趋于一致,并稳定在100%.但是信噪比在低于-2dB时,成功概率低于80%,2种算法在低信噪比时已经不可取.在信噪比小于0dB时,相对来说,MRM算法的成功概率小于PRM算法. 仿真条件如实验2,MRM算法和PRM算法在不同信噪比对应的RMSE(均方根误差)的仿真结果如图4.由图4可以看出,随着信噪比的增加,MRM算法和PRM算法的RMSE逐渐逼近0,并最终趋于一致.在信噪比为0dB时,PRM算法的RMSE约为0.28°,而MRM算法的约为0.44°,并且,随着信噪比的降低,2种算法的差距越来越大.从RMSE来看,PRM算法性能较优,适用于信噪比较低的情况. 本文讨论了2种快速波达方向估计的算法:PRM算法和MRM算法.通过复杂度分析可以得出,2种算法都不需要计算量特别大的数据协方差特征值分解和谱峰搜索过程,具有运算量小、收敛速度快、稳定性好等优点.从复杂度来说,MRM算法的复杂度低于PRM算法的,MRM算法适用于对复杂度要求较高的情况.由仿真结果可知,这2种算法都能准确地估计信源的DoA.在低信噪比时,MRM算法的检测成功概率比PRM算法的低,MRM算法的RMSE比PRM算法的高.因此,PRM算法在低信噪比时性能比MRM算法更好,而MRM算法更适于在高信噪比运用. [1]张小飞,汪飞,徐大专.阵列信号处理的理论和应用[M].北京:国防工业出版社,2010:11. [2]刘剑,黄知涛,周一宇.基于扩展传播算子的非圆信号测向方法[J].信号处理,2008,24(4):556-560. [3]孙心宇,周江建.非圆传播算子DOA估计算法[J].数据采集与处理,2013,28(3):313-318. [4]SHEND,CHENJS,GONGJ.PolynomialrootingalgorithmforDOAestimationbasedonsignalsubspace[C]//4thInternationalCongressonImageandSignalProcessing.Shanghai:IEEE,2011:2 617-2 620. [5]ENRIQUEAS,MOHAMMADS.Noisesubspace-basediterativetechniquefordirectionfinding[J].IEEETransactionsonAerospaceandElectronicSystems,2013,49(4):2 281-2 295. [6]黄磊,吴顺君,张林让.一种波达方向估计的快速算法[J].电波科学学报,2005,20(6):707-711. [7]黄磊,吴顺君,张林让,等.快速子空间分解及其维数的快速估计[J].电子学报,2005,33(6):977-981. [8]RICKSDC,GOLDSTEINJS.Efficientimplementationofmulti-stageadaptivewienerfilters[C]//Proceedingsofthe24thAntennaApplicationsSymposium.AllertonPark:IEEE,2000:29- 41. [9]包志强,吴顺君,张林让.一种信源个数与波达方向联合估计的新算法[J].电子学报,2006,34(12):170-174.[10]李堰,宋爱民,刘剑.非圆信号多级维纳滤波MUSIC测向算法[J].信号处理,2011,27(5):653-657. (责任编辑雨松) Fast DoA Estimation Based on Root-MUSIC Algorithm WANG Xinhe1,ZHOU Wei1,2 (1.Chongqing Key Laboratory of Mobile Communications Technology,Chongqing University of Posts and Telecommunications,Chongqing 400065,China;2.College of Optoelectronic Engineering,Chongqing University of Posts and Telecommunications,Chongqing 400065,China) Two fast DoA algorithms were discussed to reduce complexity by classical algorithm,root-MUSIC algorithm based on propagator method and root-MUSIC algorithm using multistage Wiener filter.By propagator method,we got propagator through dividing covariance matrix,built the noise subspace,and then estimate DoA by combining root-MUSIC algorithm.By using multistage Wiener filter,we obtained the signal subspace without estimating covariance matrix,and through forward recursion of the Wiener filter,we calculated Wiener-Hoff equation,which obtain the product of the noise subspace and its conjugate transpose,and finally,according to the orthogonal projection principle,we estimated DoA by combining root-MUSIC algorithm.Neither of these two algorithms requires eigen-values decomposition of the covariance matrix or searching the peak of the spectrum,and the complexity is reduced greatly by the mathematical analysis. estimation of DoA;multistage Wiener filter;propagator;root-MUSIC algorithm 2015-07-17 2015-09-07 国家高技术研究发展计划(863计划)重点项目(2009AA011302);重庆邮电大学研究生教育创新计划重点项目(Y201019);重庆市教委科研项目(KJ090513);重庆市科委重点实验室专项项目 王新贺(1989-),男,硕士研究生,研究方向为无线移动通信、阵列信号处理.通讯作者:周围(1971-),男,教授,博士,研究方向为无线移动通信技术、通信系统及信号处理、智能天线技术等.E-mail:zhouwei1020@263.net TN929.5 A 1673-4432(2016)03-0057-04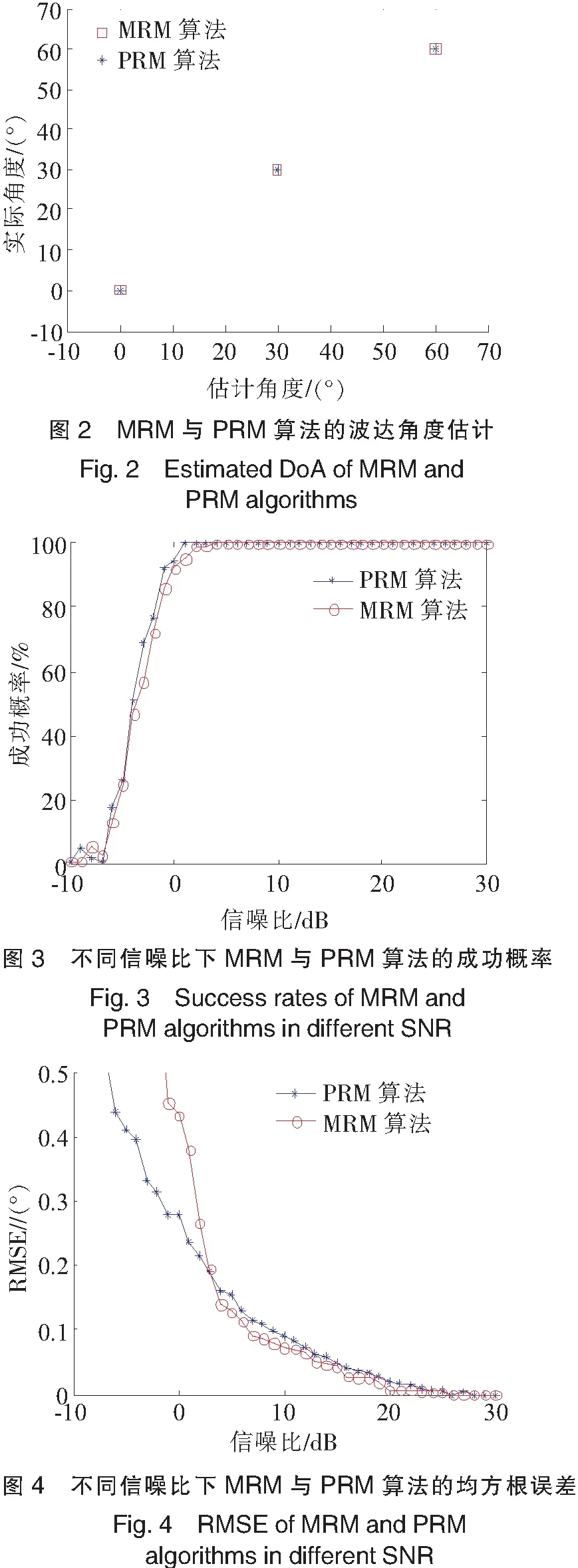
4 仿真
5 结论

