引调水工程水源地水量水质联合风险研究

徐　聪，冯民权

(西安理工大学 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048)



引调水工程水源地水量水质联合风险研究

徐聪，冯民权

(西安理工大学 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048)

【目的】 分析引调水工程水源地水量水质联合风险，为引调水工程的顺利建设提供科学依据。【方法】 利用水质综合指数评价法对水质进行评价，分别利用水质综合指数和污染最为严重的指标与水量数据进行Copula水量水质联合分布函数的构建，并以引沁入汾工程为例对引调水工程水量水质联合风险进行研究。【结果】 引沁入汾工程水源地水质状况良好，总体均能达到水质功能区Ⅳ类水要求；通过水量与水质综合指数计算得到的联合风险可以看出：就整个调水时期而言，有利于调水的概率为99.29%，不利于调水的概率为2.01%；通过水量与污染最为严重的水质指标TN计算得到的联合风险可以看出：就整个调水时期而言，有利于调水的概率为32.16%，不利于调水的概率为69.16%。【结论】 引沁入汾工程水源地适合作为该工程的取水源地，但以后需加强对TN的控制和治理。

引沁入汾工程；水质综合指数评价法；Copula函数；水量水质联合风险

随着国民经济的快速发展和人民生活质量的不断提高，人们对水资源的需求和环境要求越来越高，一些原有的人类生存区域和空间的水资源已不能满足本区域国民经济发展和人类生活的需求。由于我国人均水资源总量不足及水资源时空分布不均匀，使我国许多地区的经济社会发展受制于水资源的供给能力，因而引调水工程应运而生。然而，引调水工程势必会对水源地的水量水质等带来一定的风险，对引调水工程水源地水量水质联合风险的研究可为工程建设提供科学依据。

目前，有关Copula函数在引调水工程方面的研究已有很多，但这些研究多基于径流丰枯遭遇[1-9]、降水丰枯遭遇[10-13]和洪水遭遇[14-16]层面，少有基于水量水质联合风险的研究。少数作者利用Copula函数仅对水量水质联合分布进行了研究，但并未对联合风险进行具体分析[17]。基于此，本研究利用Copula函数从2个角度对水源地水量水质联合风险进行研究，在构建Copula水量水质联合分布函数时，首先选取多个水质指标并引入水质综合评价的思想，基于水质综合指数评价法使用简便、评价结果直观及精确度和信息利用率高的优点，利用此方法对水源地水质进行综合评价，以便较完整地反映水污染程度[18]，并利用水质综合指数作为水质基础数据，进行联合分布函数的构建，从而进行联合风险分析；其次选择水质指标中污染最为严重的一个指标作为水质基础数据，进行联合分布函数的构建及联合风险分析。最后以引沁入汾工程为例进行分析，旨在通过对取水源地水量水质联合风险的综合评价，为取水源地的选择和后期水量水质的监测管理提供参考。

1　理论基础

1.1Copula函数

Copula函数是边缘分布为[0,1]区间均匀分布的联合分布函数，总体上可以分为椭圆型、阿基米德型和二次型3类，其中生成元为1个参数的阿基米德型Copula函数的应用最为广泛，其构造形式为：

Cθ(u,v)=φ-1[φ(u)+φ(v)],0≤u,v≤1。

(1)

式中：Cθ(u,v)为Copula函数，u、v为边界分布函数，θ为参数，φ为Copula函数的生成元。

由式(1)所示的阿基米德型Copula函数的定义可知，只要算子的表示形式已知，就可确定一种相应的Copula函数形式。不同算子的选择会产生不同类别的阿基米德型Copula函数。几种常见的二维阿基米德型Copula函数[19]如表1所示。

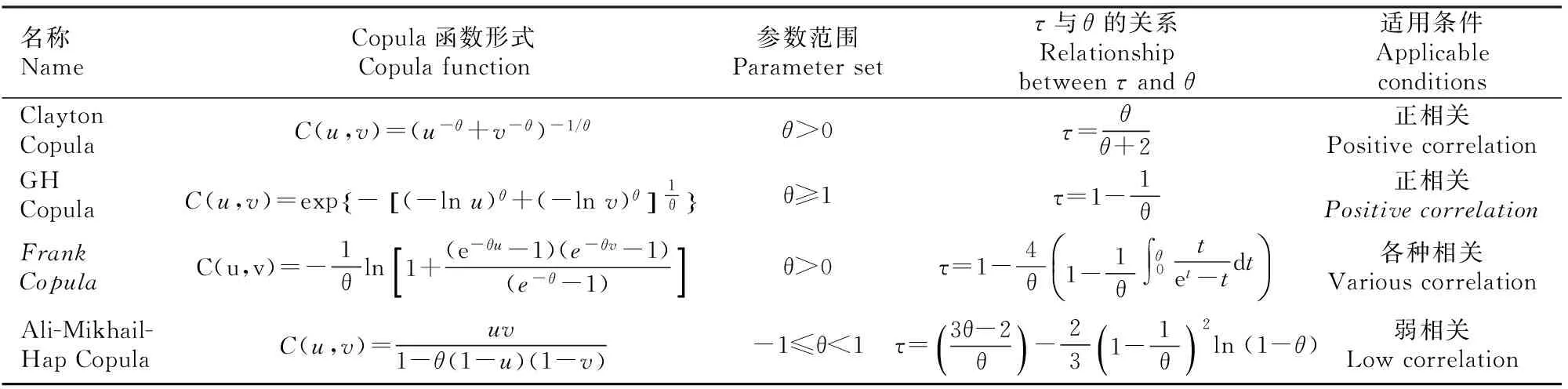
表 1　几种常见的二维阿基米德型Copula函数Table 1　Several common two-dimensional Archimedean Copula functions

注：Frank Copula函数τ与θ关系式中的t(t∈[0,θ])表示变量。

Note：t(t∈[0,θ])represents a variable in the relationshipτandθin Frank Copula function.

表1中的τ是可以描述变量之间非线性相关关系的Kendall相关系数，可由下式计算：

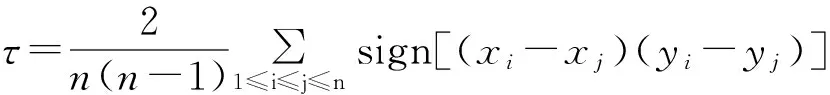
(2)

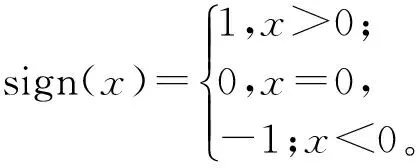
1.2Copula函数的拟合优度检验

对一组数据系列，有多个不同Copula函数可供选择，其中最优的模型需要通过拟合优度检验进行优选[7]。Copula函数的拟合优度检验有多种方法，本研究拟选用以下方法进行拟合优度检验。

应用双样本K-S进行检验，双样本K-S检验统计量的定义为：

(3)

式中：Ci为联合观测样本(xi,yi)的Copula值，ni为联合观测样本中满足x≤xi、y≤yi的联合观测个数，n为样本个数。

为了检验Copula函数的拟合优度，采用普通最小二乘法(OLS)的最小准则进行评价，离差平方和OLS的定义如下：

(4)

式中：Pei为联合分布的经验频率，Pi为联合分布的理论频率。

1.3水质综合指数评价法

水质综合指数评价法参考GB 3838-2002《地表水环境质量标准》的5级划分原则进行，定义转化指数[20]为：

(5)

式中：Si max为标准中i指标的最高级限值；Si min为i指标可能的最低值，假定Si min=0。

将所有评价项目的各等级浓度限值做统一的规范化处理，规范化公式如下：

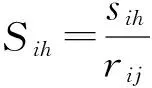
(6)

式中：i=1,2,…，n；h=1,2,…，m；sih为第i个项目的h级限值；rij为第i个项目的转化指数。

计算各级评价标准的综合指数，有：

(7)

确定实测样本的指数为：

(8)

式中：Xij为i个指标的第j个实测值。

计算实测样本综合指数为：

(9)

2　水源地水量水质联合风险分析

本研究以引沁入汾工程为背景，对其水源地水量水质的联合风险进行研究。引沁入汾工程是在安泽县和川镇岭南村兴建和川取水输水工程，开凿分水岭-草峪岭隧洞，经新建五马水库调节，调水至汾河流域的大型跨流域自流引水工程，不仅可有效缓解汾东地区严重缺水的供需矛盾，改善当地生态环境，还可为汾河下游段实现清水复流做出积极贡献。引沁入汾工程平面示意图如图1所示。

图 1　山西临汾市引沁入汾工程平面示意图

2.1基于水质综合指数的水量水质联合风险分析

2.1.1基础数据(1)水量数据。采用引沁入汾工程水源地飞岭水文站1980-2010年的年径流量数据，作为构建Copula水量水质联合分布函数的基础数据。该水文站的实测年径流量时序如图2所示。

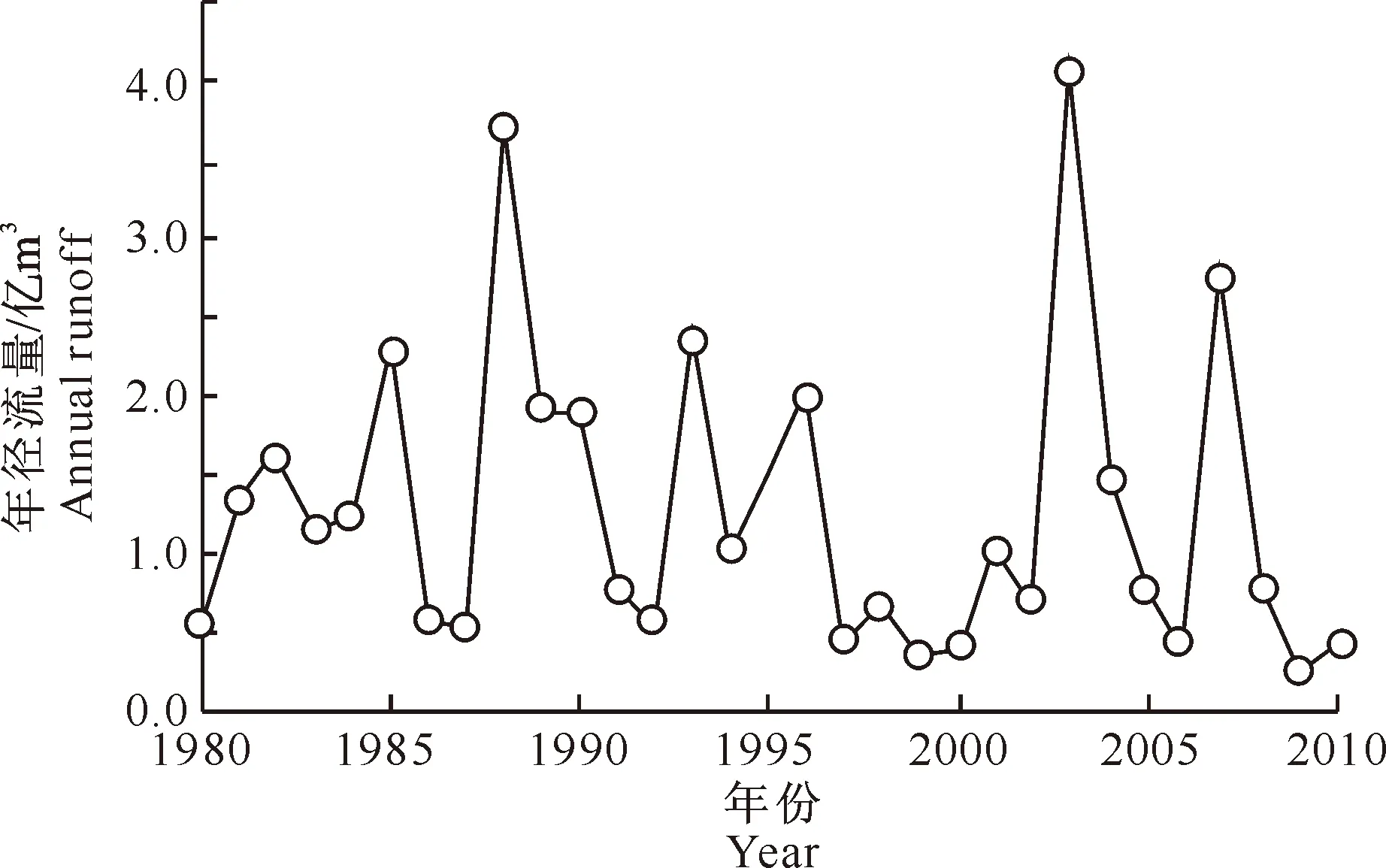
图 2　飞岭水文站实测年径流量时序图

(2)水质数据。采用引沁入汾工程水源地飞岭水文站1980-2010年水质实测数据中的6个指标(高锰酸盐指数及COD、TP、NH3-N、TN与挥发酚含量)作为水质评价的基础数据，运用水质综合指数评价法对水质进行评价，得出水质综合指数值I。然后利用表2的综合指数法地表水环境质量等级划分标准对飞岭站进行水质综合指数评价，得到的结果如表3所示。

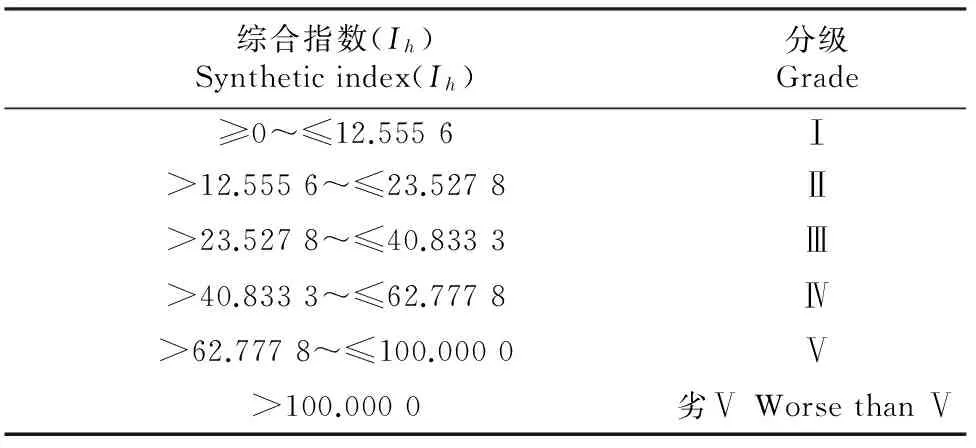
表 2　地表水环境质量等级划分标准Table 2　Division standard of surface water environmental quality

表 3　基于水质综合指数评价法的沁河飞岭水文站1980-2010年的水质评价结果Table 3　Water quality assessment at Feiling station of Qin River from 1980 to 2010 based on synthetic index method

由于引沁入汾工程的输水工程坝址位于安泽县城北的沁河干流上，而沁河为黄河的一级支流，根据《山西省地表水域环境管理区域方案》，工程所在区域为工业用水功能，执行《地表水环境质量标准》(GB 3838-2002)中Ⅳ类水标准。因而，由表2和表3可以看出，引沁入汾工程水源地水质状况良好，总体均能达到水质功能区Ⅳ类水要求。表3中的水质综合指数I值，即为构建联合分布函数所用的水质数据。

2.1.2边缘分布Copula函数方法不受变量边际分布形式的限制，对于单变量水文数据系列的分析，在我国常假定水文变量服从皮尔逊Ⅲ型(P-Ⅲ)分布。因此，本部分选用P-Ⅲ型，其分布表达式为：

(10)

采用矩法对P-Ⅲ型分布进行参数估计，得到飞岭水文站水量和水质分布参数的估计值如表4所示。

表 4　飞岭水文站水量和水质二维边缘分布函数的参数估计值Table 4　Parameter estimation of two-dimensional edge distribution function

2.1.3Copula函数参数估计和类型选择计算所得到的Kendall系数τ=-0.165 6，呈弱负相关关系。从各Copula函数对变量相关关系的要求来看：Frank Copula、Ali-Mikhail-Hap Copula函数适用于本研究的数据序列，可以根据这2种函数来确定θ、D、OLS。各参数具体计算结果如表5所示。

表 5　Copula函数各参数计算结果Table 5　Parameter calculation of Copula function

由表5可知，Frank Copula函数的OLS值为0.091 6，Ali-Mikhail-Hap Copula函数的OLS值为0.101 3，所以，本研究选用Frank Copula函数作为水量水质联合分布函数。

采用以下公式计算二维联合分布的经验频率，即：

H(x，y)=P(X≤xi,Y≤yi)=

(11)

式中：P为满足X≤xi、Y≤yi的经验概率，Nmn为X≤xi且Y≤yi的数目，N为样本容量。

图3为利用Frank Copula函数模型得出的研究区域在不同时间尺度下水量水质联合分布的理论分布与经验点的拟合情况，其复相关系数R2=0.939 9，拟合状况良好引沁入汾工程水源地水量水质联合风险进行研究，可将水量水质的联合分布分为18种情况，其联合分布概率的计算结果如表6所示。

图 3　引沁入汾工程水源地水量水质联合分布理论分布与经验点的拟合情况

对是否有利于调水，本研究规定，在水量水质联合分布的18种情况中，若水源地水质达标(即优于或等于Ⅳ类水)，则有利于调水；反之，则不利于调水。由表6可以看出，丰水期、平水期、枯水期水质达标的分布概率分别为33.67%，15.46%，50.16%，因水质原因，有利于调水的概率为99.29%。同样可得，丰、平、枯水期水质不达标的概率分别为0.68%，0.31%，1.02%，因水质不达标而不利于调水的概率为2.01%。总体而言，引沁入汾工程水源地径流量无论处于哪种状态，水质不达标的概率均较小。在不利于调水的组合中，处于枯水期且水质不达标为最不利调水情况，其概率为1.02%；在有利于调水的组合中，处于丰水期且水质达标为最有利调水情况，其概率为33.67%，处于枯水期且水质达标为有利调水最少的情况，其概率为50.16%。

若已知径流量的丰枯状态，可用条件概率的计算来预测水质情况。若已知径流处于丰水期，则预测水质超标的概率为：

P(Y>62.777 8|X≥1.473 8)=

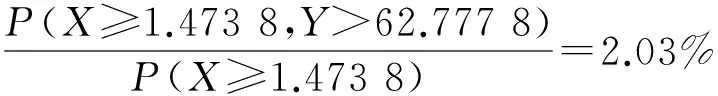
若径流处于平水期，则预测水质超标的概率为：

P(Y>62.777 8|1.089 4

若径流处于枯水期，则预测水质超标的概率为：

P(Y>62.777 8|X≤1.089 4)=

从条件概率的计算可以看出：无论径流量处于哪种状态，所预测水质的超标概率均较小。

2.2基于TN的水量水质联合风险分析

采用引沁入汾工程水源地飞岭水文站1980-2010年的年径流量数据和污染最为严重的水质指标TN作为构建Copula水量水质联合分布函数的基础数据。经过对比分析，水量采用P-Ⅲ型分布，水质指标TN采用Gumbel分布。经计算Frank Copula函数适合作为该联合分布的函数。

根据所建立的模型对引沁入汾工程水源地水量水质联合风险进行研究，可将水量与TN的联合分布分为18种情况，具体情况及计算结果如表7所示。在表7水量水质联合分布的18种情况中，若水源地TN达标(即优于或等于Ⅳ类水中TN的标准)，则有利于调水；反之，则不利于调水。经过分析可以得出：就整个调水时期而言，有利于调水的概率为32.16%，不利于调水的概率为69.16%。在不利于调水的组合中，处于枯水期且TN不达标为最不利调水情况，其概率为34.96%；在有利于调水的组合中，处于丰水期且TN达标为最有利调水情况，其概率为10.91%，处于枯水期且TN达标为有利调水最少的情况，其概率为16.23%。

表 7　基于TN的引沁入汾工程水源地水量水质风险的联合分布概率Table 7　Joint distribution probability of water quantity and quality risk of water sources of water diversion project from Qin River to Fen River based on TN 　%

3　结　论

(1)引沁入汾工程水源地水质状况良好，总体均能达到水质功能区Ⅳ类水要求。

(2)通过水量与水质综合指数计算得到的联合风险可以看出：就整个调水时期而言，有利于调水的概率为99.29%，不利于调水的概率为2.01%。在不利于调水的组合中，处于枯水期且水质不达标为最不利调水情况，其概率为1.02%；在有利于调水的组合中，处于丰水期且水质达标为最有利调水情况，其概率为33.67%，处于枯水期且水质达标为有利调水量最少的情况，其概率为50.16%。

(3)通过水量与污染最为严重的水质指标TN计算得到的联合风险可以看出：就整个调水时期而言，有利于调水的概率为32.16%，不利于调水的概率为69.16%。在不利于调水的组合中，处于枯水期且TN不达标为最不利调水情况，其概率为34.96%；在有利于调水的组合中，处于丰水期且TN达标为最有利调水情况，其概率为10.91%，处于枯水期且TN达标为有利调水最少的情况，其概率为16.23%。

由此可以看出：引沁入汾工程水源地适合作为该取水工程的取水源地，但以后需加强对TN的控制和治理，该研究结果既可为引调水工程水源地水量水质联合风险的研究提供借鉴，也可为引调水工程的建设提供科学依据。

[1]莫淑红,沈冰,张晓伟,等.基于Copula函数的河川径流丰枯遭遇分析 [J].西北农林科技大学学报(自然科学版),2009,37(6):131-136.

Mo S H,Shen B,Zhang X W,et al.Synchronous-asynchronous encounter probability of rich-poor runoff based on Copula function [J].Journal of Northwest A&F University(Nat Sci Ed),2009,37(6):131-136.

[2]丁志宏,冯平,张永.基于Copula模型的丰枯频率分析：以南水北调西线工程调水区径流与黄河上游来水的丰枯遭遇研究为例 [J].长江流域资源与环境,2010,19(7):759-764.

Ding Z H,Feng P,Zhang Y.Rich poor frequency analysis of runoff based on Copula model：a case study on encounter probability of rich-poor runoff between rivers in area of western route of south to north water transfer project and that of the upper reach of the Yellow river [J].Resources and Environment in the Yangtze Basin,2010,19(7):759-764.

[3]张忠波,张双虎,王浩.基于Copula函数的三峡工程供水期丰枯遭遇分析 [J].人民长江,2012,43(3):5-8.

Zhang Z B,Zhang S H,Wang H,Analysis of wetness:dryness encounter in TGP water supply period based on Copula function [J].Yangtze River,2012,43(3):5-8.

[4]谢华,罗强,黄介生. 基于三维copula函数的多水文区丰枯遭遇分析 [J].水科学进展,2012,23(2):186-193.

Xie H,Luo Q,Huang J S.Synchronous asynchronous encounter analysis of multiple hydrologic regions based on 3D copula function [J].Advances in Water Science,2012,23(2):186-193.

[5]何庆升,朱永忠.应用高维Copula函数的月径流量联合概率分布研究 [J].重庆理工大学学报(自然科学版),2013,27(8):112-120.

He Q S,Zhu Y Z.Studying of annual flow joint probability distribution based on high dimensions Copula function [J].Journal of Chongqing University of Technology(Natural Science Edition),2013,27(8):112-120.

[6]Jeong C,Lee T.Copula-based modeling and stochastic simulation of seasonal intermittent streamflows for arid regions [J].Journal of Hydro-environment Research,2015,9(4):604-613.

[7]冯民权,郝竹林,张园园,等.禹门口调水工程水源区与受水区径流丰枯遭遇风险分析研究 [J].自然灾害学报,2012,21(6):156-163.

Feng M Q,Hao Z L,Zhang Y Y,et al.Risk analysis of runoff rich poor encounter between water source area and receiving area of Yumenkou water transfer project [J].Journal of Natural Disasters,2012,21(6):156-163.

[8]Yu K X,Xiong L H,Lars G.Derivation of low flow distribution functions using copulas [J].Journal of Hydrology,2014,508:273-288.

[9]牛军宜,冯平,丁志宏.基于多元Copula函数的引滦水库径流丰枯补偿特性研究 [J].吉林大学学报(地球科学版),2009,39(6):1095-1100.

Niu J Y,Feng P,Ding Z H.Study of the wetness-dryness compensation characteristics of Luan River diversion reservoirs’ inflow based on multivariate Copula Functions [J].Journal of Jilin University(Earth Science Edition),2009,39(6):1095-1100.

[10]郑红星,刘昌明.南水北调东中两线不同水文区降水丰枯遭遇性分析 [J].地理学报,2000,55(5):523-532.

Zheng H X,Liu C M.Analysis on a synchronism-synchronism of regional precipitation in planned South-to-North water transfer areas [J].Acta Geographica Sinica,2000,55(5):523-532.

[11]熊其玲,何小聪,康玲.基于Copula函数的南水北调中线降水丰枯遭遇分析 [J].水电能源科学,2009,27(6):9-11，112.

Xiong Q L,He X C,Kang L.Synchronous asynchronous encounter probability of rich poor precipitation between water source area and water receiving area based on Copula theory in middle route of South to North water transfer project [J].Water Resources and Power,2009,27(6):9-11，112.

[12]王伟,钟永华,雷晓辉,等.引汉济渭工程水源区与受水区丰枯遭遇分析 [J].南水北调与水利科技,2012,10(5):23-26，36.

Wang W,Zhong Y H,Lei X H,et al.Synchronous-asynchronous encounter probability of rich-poor precipitation between water source area and water receiving area of the Hanjiang-to-Weihe River water transfer project [J].South-to-North Water Transfers and Water Science & Technology,2012,10(5):23-26，36.

[13]Zoubeida K B,Andras B.Modeling short duration extreme pr-ecipitation patterns using copula and generalized maximum pseudo-likelihood estimation with censoring [J].Advances in Water Resources,2015,84:1-13.

[14]陈璐,郭生练,张洪刚,等.长江上游干支流洪水遭遇分析 [J].水科学进展,2011,22(3):323-330.

Chen L,Guo S L,Zhang H G,et al.Flood coincidence probability analysis for the upstream Yangtze River and its tributaries [J].Advances in Water Science,2011,22(3):323-330.

[15]李伟.Copula函数在多变量洪水联合分布中的应用研究 [D].武汉：华中科技大学,2013.

Li W.The application and research of multivate flood joint distribution based on Copula theory [D].Wuhan:Huazhong University of Science and Technology,2013.

[16]Fan Y R,Huang W W,Huang G H,et al.Hydrologic risk analysis in the Yangtze River basin through coupling Gaussian mixtures into copulas [J].Advances in Water Resources,2016,88:170-185.

[17]张翔,冉啟香,夏军,等.基于Copula函数的水量水质联合分布函数 [J].水利学报,2011,42(4):483-489.

Zhang X,Ran Q X,Xia J,et al.Jointed distribution function of water quality and water quantity based on Copula [J].Journal of Hydraulic Engineering,2011,42(4):483-489.

[18]陈仁杰,钱海雷,阚海东，等.水质评价综合指数法的研究进展 [J].环境与职业医学,2009,26(6):581-584.

Chen R J,Qian H L,Kan H D,et al.A review of comprehensive index methods in water quality assessment [J].Journal of Environmental & Occupational Medicine,2009,26(6):581-584.

[19]Zhang L.Multivariate hydrological frequency analysis and risk mapping [D].Baton Rouge:Louisiana State University,2005.

[20]李凡修,陈武,梅平，等.浅层地下水环境质量评价的综合指数模型 [J].地下水,2004,26(1):36-37.

Li F X,Chen W,Mei P,et al.Synthetic index model of shallow groundwater environment quality evaluation [J].Ground Water,2004,26(1):36-37.

Joint risk of water quantity and quality in water sources of water diversion project

XU Cong,FENG Minquan

(StateKeyLaboratoryBaseofEco-hydraulicEngineeringinAridArea,Xi’anUniversityofTechnology,Xi’an，Shaanxi710048,China)

【Objective】 This paper studied the joint risk of water quantity and quality in water sources of water diversion project to provide scientific basis for successful construction of water diversion project.【Method】 Water quality was evaluated by synthetic index method.Water quantity data was used together with water quality synthetic index and the most serious pollution indicator to build the Copula joint distribution function.Then,the joint risk of water quantity and quality was investigated using the water diversion project from Qin River to Fen River as an example.【Result】 The water sources of water diversion project from Qin River to Fen River have good water quality,and the overall water quality reaches ribbon Class Ⅳ water requirements.From the joint risk calculated by water quality and quantity synthetic index,the probability that is conducive to diversion is 99.29%,and the probability that is not conducive to diversion is 2.01% during the entire water diversion period.From the joint risk of water contamination by the most serious water quality indicator TN,the probability that is conducive to diversion is 32.16% and the probability that is not conducive to diversion is 69.16%.【Conclusion】 The water sources of water diversion project from Qin River to Fen River is suitable and the control and governance of TN should be strengthened in future.

water diversion project from Qin River to Fen River;synthetic index method for water quality assessment;Copula function;joint risk of water quantity and quality

时间:2016-08-0909:41DOI：10.13207/j.cnki.jnwafu.2016.09.031

2015-02-06

高等学校博士学科点专项科研基金项目(20126118110015)；中央财政支持地方高校发展专项资金特色重点学科项目(106-00X101，106-5X1205)；山西省中部引黄工程管理局计划基金项目(2014-9)

徐聪(1990-)，男，河南长葛人，在读硕士，主要从事水环境模拟与预测研究。E-mail:1064974686@qq.com

冯民权(1964-)，男，山西永济人，教授，博士，博士生导师，主要从事水环境模拟与污染控制研究。

E-mail:mqfeng@xaut.edu.cn

X824.04

A

1671-9387(2016)09-0228-07

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20160809.0941.062.html