基于数字形态学滤波与SVM技术的帘子布疵点检测

温盛军， 常保磊， 蒋成龙， 张五一

(中原工学院， 郑州450007)



基于数字形态学滤波与SVM技术的帘子布疵点检测

温盛军， 常保磊， 蒋成龙， 张五一

(中原工学院， 郑州450007)

针对帘子布生产过程中可能出现的瑕疵问题，提出了一种多形态多尺寸的数字形态学滤波方法，采用多种不同形状和大小的结构元素对帘子布疵点图像进行滤波，对滤波后的图像使用大律法阈值分割，并提取疵点的长、宽、长宽比、面积等特征。最后，利用支持向量机(SVM)进行疵点识别。实验结果表明，该方法可准确检测帘子布中浆斑、经线粘连、断经、劈缝等主要疵点，具有分类准确、辨别速度快的优点，疵点识别率达93.3%。

疵点检测；数字形态学；支持向量机；帘子布

在帘子布生产过程中，疵点检测是必不可缺少的环节。目前我国的检测技术相对落后，传统检测大多以人工检测为主，工作强度高、时间长，由于受检测人员主观因素的影响，无法保证疵点检测的准确[1-2]。随着人工智能和图像处理技术的迅速发展，基于图像分析的织物疵点检测技术已取代传统的人工视觉检测，成为织物疵点检测领域的研究热点[3-8]。帘子布表面经纬线有典型的构造，具有显著的方向性、周期性及均匀性，而织物疵点的存在，打乱了经线纹理在频率及方向上的协调一致[9]。传统的数字图像处理方法采用一个结构元素对图像进行分析，疵点识别效果不理想，尤其是在对图像进行形态学边缘检测时，一个结构元素只对与其同方向的边缘敏感，而与其不同方向的边缘则会被平滑掉[10-13]。本文提出了一种基于多结构多尺寸数字形态学处理的帘子布疵点检测技术。该方法通过多结构多尺寸数字形态学对图像进行滤波，使用大律法对滤波后的图像进行阈值分割，提取疵点的长度、宽度、长宽比、面积等特征，并把提取的特征值通过支持向量机进行训练建模， 利用模型对比，实现疵点的分类识别。

1　基于多结构多尺寸数字形态学的图像滤波

数字形态学利用具有特定形态的构造元素来衡量和提取图像中的对应形状，并对图像进行分析和辨别。形态学的处理可以在保持图像原有基本形状的同时，简化图像数据，并且去除图像中一些不相关的结构。具体步骤为：先将原始图像通过直方图均衡化预处理，再对处理后的均衡化图像进行高斯滤波，然后用多结构多尺寸数字形态学滤波器对高斯滤波处理后的图像进行滤波。

1.1直方图均衡化

直方图的横坐标、纵坐标分别表示图像的灰度值和出现灰度值的概率，不反映像素的空间位置所在，只统计每一种灰度级在图像中出现的次数或概率。直方图均衡化是通过控制灰度级的概率密度函数，尽可能使每种灰度像素个数相等或均匀分布，加强直方图统计中所占比例高的像素的灰度值，减少直方图中比例小的灰度值所占用的灰度范围。增大亮度，使两者之间对比度变大，整体的对比度不变。

预处理采用直方图均衡化来增强图像的对比度，如图1—图4所示。由于采用的是背光照明方式，帘子布的经线较为密集，照明不充足，造成拍摄图像偏暗，正常区域和疵点区域差别显示不明显。同时，直方图均衡化可以剔除一些细小噪声造成的图像某点灰度值凸起。

对于前景和背景都太暗的帘子布浆斑、断经、经线粘连、劈缝图像，经过直方图均衡化后，可加强图像中比例高的像素的灰度值，减小图像中比例小的灰度值所占用的灰度范围。因此，图像亮度增大，前景和背景之间对比度变大，整体对比度不变。

1.2高斯低通滤波器

高斯滤波是对图像中的背景与前景作模糊处理，同时保留图像疵点的边缘特征。当滤波器的模板尺寸大时，高斯滤波能很好地保持疵点的边缘特征[10]。用高斯滤波法对图1—图4进行均衡化处理后的图像如图5所示。滤波之后，图像前景和背景模糊了，但保留了图像疵点的特征。

(a)原图像　　　　　　　　(b)均衡化后图像图1　浆斑原图像与均衡化后的图像

(a)原图像　　　　　　　　(b)均衡化后图像图2　经线粘连原图像与均衡化后的图像

(a)原图像　　　　　　　(b)均衡化后图像图3　断经原图像与均衡化后的图像

(a)原图像 　　　　　　　(b)均衡化后图像图4　劈缝原图像与均衡化后的图像

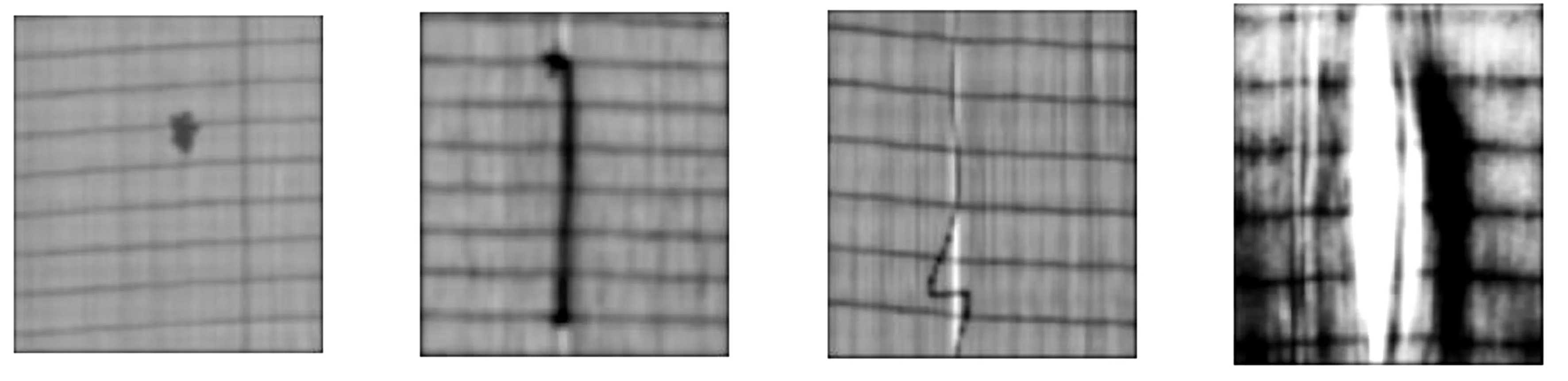
(a)浆斑　　　　　　　(b)经线粘连　　　　　　　(c)断经　　　　　　　　　(d)劈缝图5　高斯滤波结果图

1.3多结构多尺寸数字形态学滤波

1.3.1二值灰度形态学处理

数字形态学中，二值图像的形态变换是一种针对集合的处理过程。其形态算子的实质是物体或形状的集合与结构元素间的相互作用，结构元素的形状决定了运算所提取信号的形状信息。形态学基本运算包括膨胀、腐蚀、开运算、闭运算。用T(i,j)结构元素模型对原始图像I(x,y)进行腐蚀，然后进行膨胀运算，此过程称为开运算。对图像进行膨胀运算，然后进行腐蚀运算，此过程称为闭运算。利用4种基本形态学运算可以组合出多种不同图像的处理算法，以对图像形状和结构进行分析与处理，如图像分割、细化、噪声滤波、图像增强、边缘提取、形态骨架提取等。

灰度图像形态学是从二值图像形态学扩展而来的，形态学的运算对象不再是集合，而是灰度图像函数。设f(x,y)、b(s,t)分别表示二值形态学中的输入图像和结构元素，用结构元素b(s,t)对灰度图像f(x,y)进行腐蚀和膨胀运算，如下所示：

g(x,y)=min{f(x+s,y+t)-b(s,t)|(x+s,y+t)∈Df,(x,y)∈Db}

(1)

h(x,y)=max{f(x+s,y+t)+b(s,t)|(x+s,y+t)∈Df,(x,p)∈Db}

(2)

其中：g(x,y)、h(x,y)分别是腐蚀和膨胀后的灰度图像，Df和Db为f(x,y)和b(s,t)的定义域。

1.3.2多结构多尺寸检测算法

几何形状结构是形态学的基本算子，直接影响图像处理效果和质量。在实际处理不同图像应用中，只有一定的结构元素可用，且结构元素的形状和大小必须适用于目标图像的几何特征。结构元素一般分为对称结构和非对称结构，对称结构通常有圆盘、菱形、正方形、六边形等。由于对称结构元素各个方向相同，因此可以得到与方向无关的运算结果。在结构元素形状确定后，结构元素的大小也很重要。结构元素过小，开运算时不能剔除较小的无关疵点，

闭运算时不能填补物体内相连的孔洞；结构元素过大，开运算时会造成假断裂，闭运算时会造成目标过度粘连。

单个结构元素只能在单个方向上对图像进行处理。图像中的目标复杂，采取一种结构元素时，某些方向的边缘不能被检测出来，无法得到完整的图像轮廓。本文提出了一种基于多结构元素的数字形态学图像边缘检测算法。多尺寸检测利用大小不同的结构元素提取目标图像特征。大尺寸结构元素优点是去噪能力强，缺点是检测边缘较粗；小尺寸结构元素优点是检测边缘好，但去噪能力差。设b为结构元素，n为尺寸参数，多尺寸结构元素的定义为：

nb=b⊕b⊕b…⊕b

(3)

多结构元素检测采用不同形状结构提取图像特征，能更好地处理图像细节和平滑性。将不同结构检测结果合并，可得到多结构元素图像处理边缘检测结果En b(x,y)。

(4)

对于多结构多尺寸算子，由于大小不同、形状不同，使得处理结果不同，因而需要对多结构进行运算合成。

假设f′(x,y)为合成的图像，[k,l]为尺寸n的取值范围，wn为尺寸的权重，则加权合成算法如式(5)：

(5)

图6是通过5种不同算子结构对4种不同疵点进行滤波的结果图。由图6可知，不同结构元素对不同形状边缘具有不同的适应性，经过加权合成，可使图像边缘更好地保留下来。

(a)浆斑　　　　　　　(b)经线粘连　　　　　　　　(c)断经　　　　　　　　(d)劈缝图6　多尺寸多元素形态学滤波结果图

2　大律法阈值分割

大津法通过图像的灰度特征，将图像分割成背景区域和目标区域两部分，使两部分的类间方差取值最大。背景区域和目标区域的类间方差越大，构成图像的两部分的差别越明显，图像的错分概率越小。

假设图像像素总数为N，灰度范围为[0,255]，灰度为i的像素个数为ni，其概率pi为：

pi=ni/N

(6)

用阈值T将灰度图像分割为目标区域和背景区域两部分，分别用D0、D1表示。图像的总体灰度均值如式(7)所示：

(7)

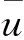
(8)

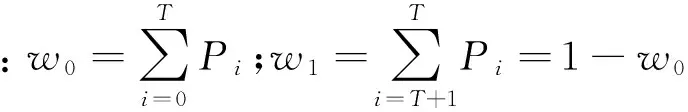
(9)

两者之间的方差为：

(10)

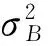
(a)浆斑　　　　　　　　(b)经线粘连　　　　　　　(c)断经　　　　　　　　　(d)劈缝图7　阈值分割图像

3　疵点检测及特征提取

3.1基于灰度比例法的疵点检测

帘子布疵点判别是一个实时动态过程，需要有快速且判断准确的算法与之匹配。疵点快速判别的主要任务是在尽可能短的时间里把带有疵点的图像检测出来，并且能够给出疵点的位置。常用的织物疵点判别都是建立在空间域上，根据正常纹理和疵点纹理的变化来进行判断。本文采用灰度比例法对疵点进行判别。该方法从帘子布自身纹理出发，结合阈值分割理论，在原理上抓住帘子布的自身特点，具有很好的适应性。

首先用大津法获取阈值T。将10幅图分别按照两个窗口进行分块，求取每块的灰度比例值，将这10幅图像对应的块相加，求取每块的均值μii和标准差σii。然后，确定判别标准μii-C1σii≤B/F≤μii+C2σii(B/F为前景与背景的比值，C1和C2为常数)。如果灰度比值B/F在此标准范围内，视为正常。按照定义好的检测窗口求取灰度比值，若灰度比值属于正常范围，定义检测窗口值为1；若μii-C1σii>B/F，说明前景占主导，定义检测窗口值为2；若μii-C1σii

以浆斑为例。以方形窗口为模板，正常帘子布的max和min在一定范围内浮动，如图8所示。浆斑在方形窗口检测下，疵点部分在窗口处灰度比例发生巨变，如图9所示。图9中，在15～20之间曲线出现一个峰值，与正常帘子布形成鲜明的对比，即可判断此处存在疵点。

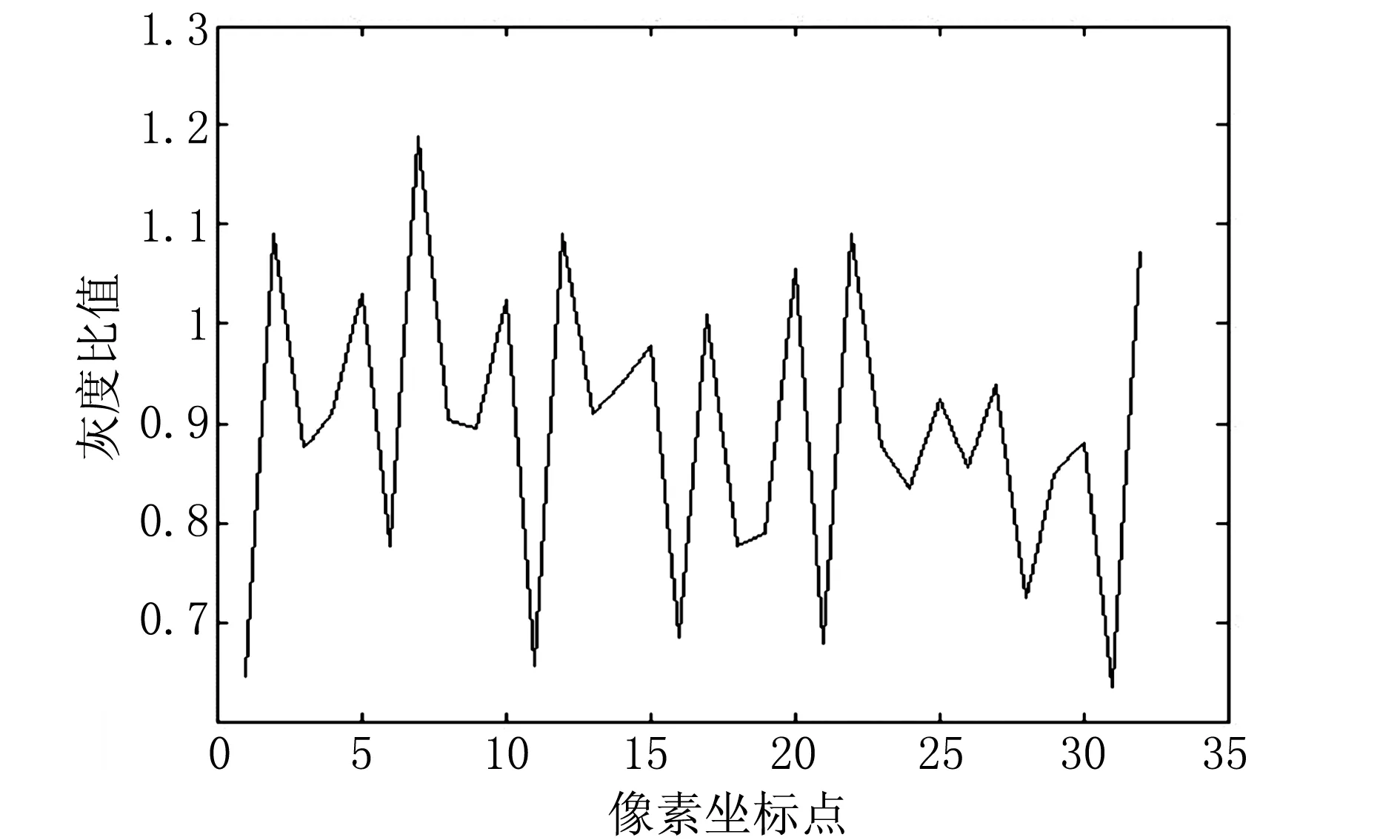
图8　正常帘子布的max和min曲线

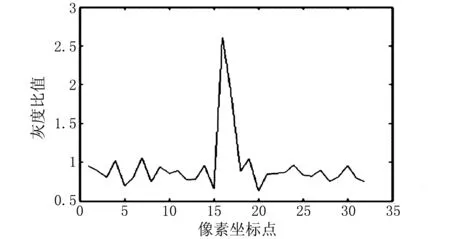
图9　浆斑疵点的max曲线

3.2疵点特征提取

对阈值分割后的图像，需要计算图像的长、宽、长宽比和面积，提取这些特征数据。找到图像疵点区域的最左方与最右方的点，通过相减得到的像素值即为疵点区域的长；找到图像疵点区域的最上方与最下方的点，通过相减得到的像素值即为疵点区域的宽；对长宽求比例，即得长宽比；计算出白色区域所覆盖的像素点的个数，即为疵点区域的面积。以上计算所得到的长、宽、面积等不是实际的图像大

小，而是用像素代表的大小。图10所示为接头疵点图像的宽度和长度，图中像素255均代表疵点的宽与长。

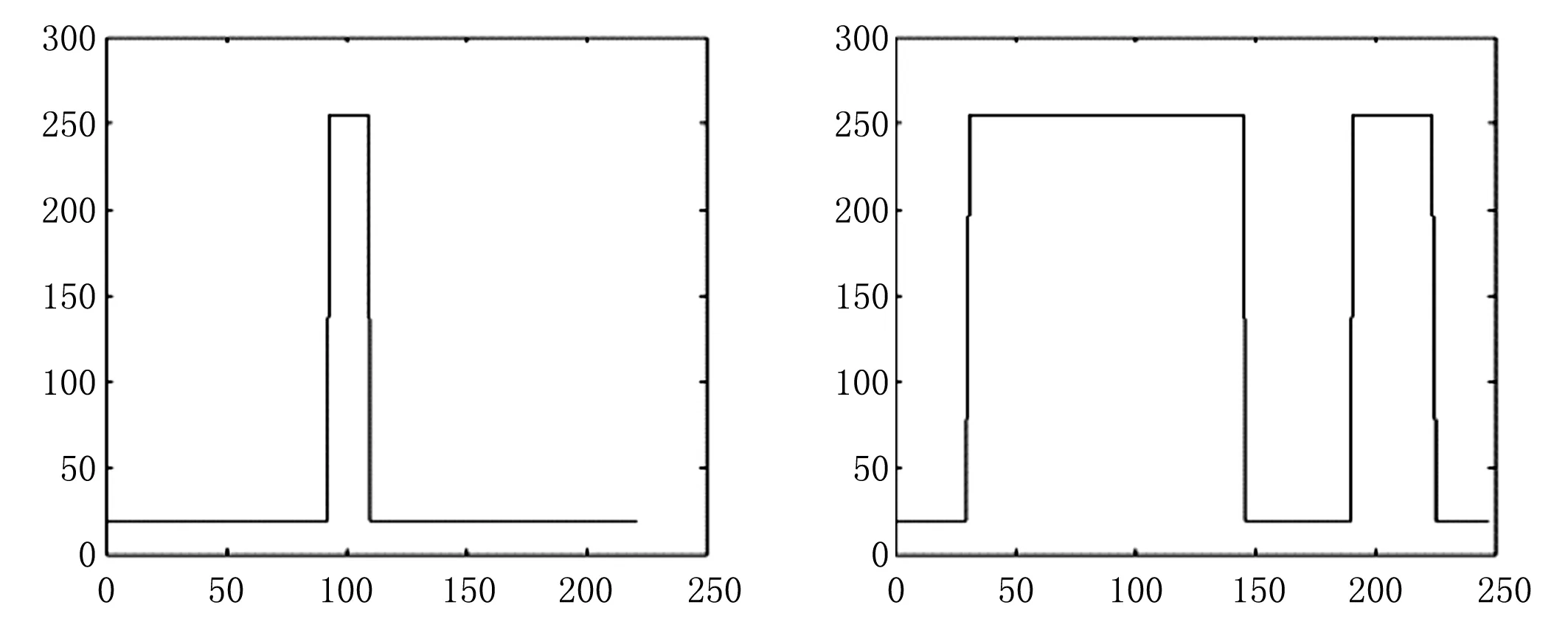
图10　疵点接头的长和宽示意图

将得到的浆斑、经线粘连、接头、劈缝等疵点的长、宽、长宽比以及面积数据存储到表格里，如图11和12所示。每种疵点选取40幅，并将4种疵点设定4种标签，分别为1、2、3、4。数据表格的前4列是输入的特征参数，最后一列是疵点的类型。这些特征数据将作为支持向量机输入的特征向量，为下一步建立SVM疵点识别模型所用。

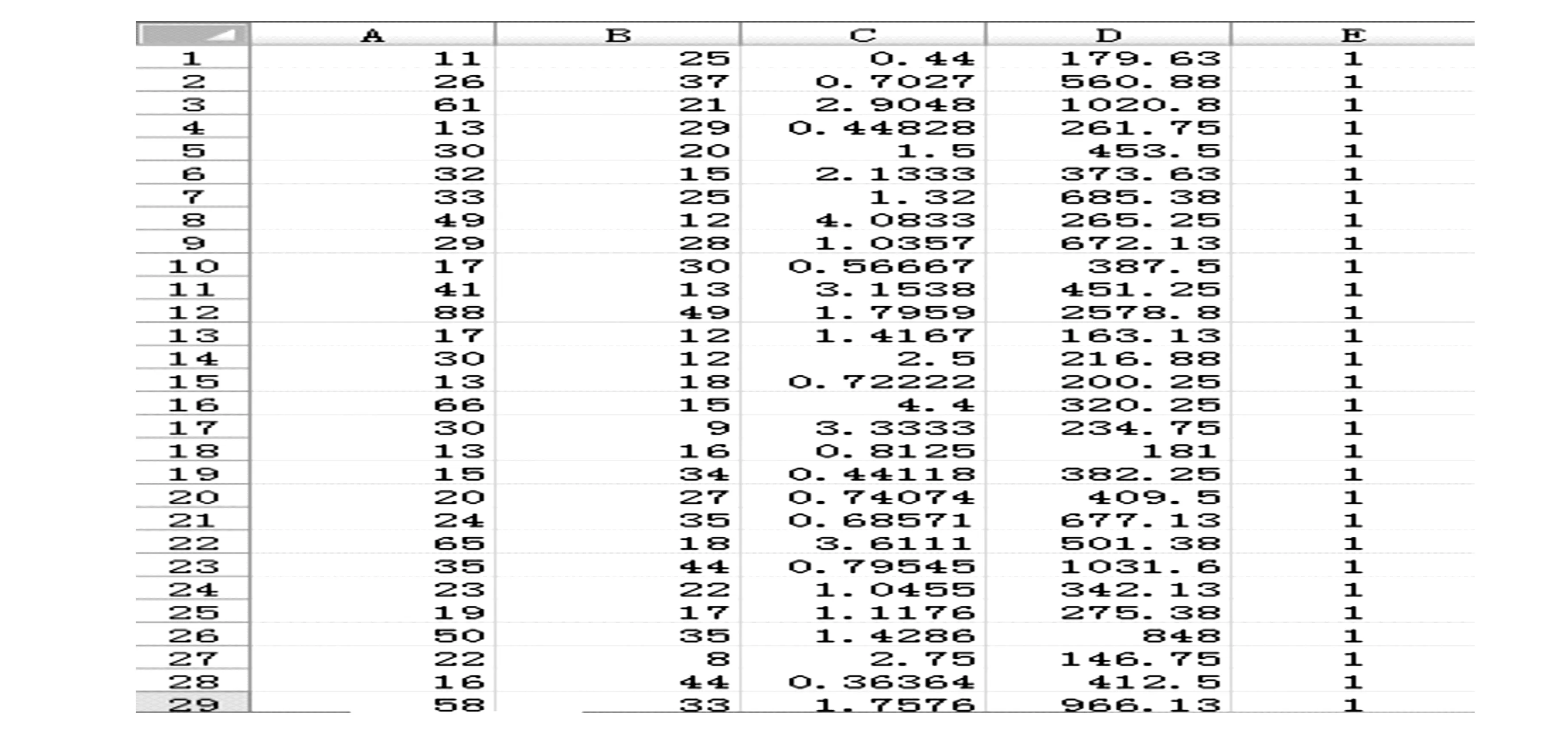
图11　训练样本1

图12　训练样本2

4　基于SVM的疵点分类识别

SVM技术通过核函数将原空间里的线性不可分数据映射到线性可分的高维特征空间中，以实现线性不可分疵点的分类识别。以前面提取的多个特征参数作为输入到支持向量机的学习样本，建立识别模型，通过SVM模型对疵点类型进行分类识别。

将上述采集的120幅图像疵点部分的长、宽、长宽比以及面积数据作为SVM的训练样本，通过svmtrain函数建立SVM模型。通过模型，用svmpredict函数对另外30组测试样本进行识别，结果如图13所示。根据测试样本的输出结果，分类识别正确率达到93.3% ，达到所需的检测要求。

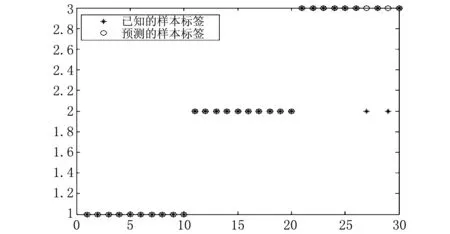
图13　测试样本输出图

5　结　语

本文结合多结构多尺寸数字形态学、大律阈值分割算法和SVM技术，进行了帘子布疵点的检测与识别。实验结果表明，采用本文所提出的方法可以快速准确判别疵点，且对浆斑、经线粘连、断经、劈缝等疵点的分类识别率达到93.3%。

[1]卿湘运,段红,魏俊民.基于局部熵的织物疵点检测与识别的研究[J].纺织学报，2004,25(5):57-59.

[2]杨杨.帘子布疵点检测系统研究[D]. 郑州：中原工学院，2014.

[3]张五一，杨扬，林聪.基于Gabor滤波器组与BP神经网络的帘子布疵点检测研究与实现[J].中原工学院学报，2014，25(3)：1-6.

[4]赵强松，张五一，王斌.基于灰度剖面直方统计的帘子布疵点识别研究[J].中原工学院学报，2009，20(5)：21-25.

[5]张五一，侯远韶，张继超.基于二维稀疏表示和范数优化的织物疵点分类研究[J].中原工学院学报，2012，23(3)：24-28.

[6]Arivazhagan S, Ganesan L, Bama S. Fault Segmentation in Fabric Images Using Gabor Wavelet Transform[J].Machine Vision and Applications,2006,16(6):356-363.

[7]袁端磊,宋寅卯.基于最优 Gabor 滤波器的织物缺陷检测[J].中国图像图形学报, 2006, 11(7): 954-958.

[8]张渤,张代林,陈幼平.用于无纺布缺陷检测的Gabor滤波器参数研究[J].武汉理工大学学报, 2012, 34(7):126.

[9]郑丽香.基于视频多帧融合的车牌识别技术研究[D]. 厦门：厦门大学，2012.

[10]宋寅卯,刘磊,李晓娟.基于改进的PCNN和SVM的织物疵点检测的算法[J].天津理工大学学报,2010,29(5):77-80.

[11]纪惠军,张小栋,杨建民.基于机器视觉的织物疵点检测技术探究[J].现代纺织技术,2011(2):11-15.

[12]余农,李予蜀,王润生.自动检测图像目标的形态滤波遗传算法[J].计算机学,2001;24(4):336-346.

[13]张家. 树灰度图像的最大最小优化熵阈值分割[J].电讯技术,1955,35(6):42-45.

(责任编辑：席艳君)Defect Detection Based on Mathematical Morphology Processing and Support Vector Machines for Tyre Fabric

WEN Sheng-jun， CHANG Bao-lei， JANG Cheng-long， ZHANG Wu-yi

(Zhongyuan University of Technology， Zhengzhou 450007, China)

In view of the defect problem in production process of tyre fabric, a multi mathematical morphological structure and more size based filter method is proposed to filter the tyre fabric images with defect using different size and structure element. Then, the filtered image is separated by a big law threshold, and the characteristics of the defect are extracted, including length, width, shape features and area. Finally, support vector machine is used to identify the defect via the extracted characteristics. Experimental results show that the presented method can accurately detect the defects, such as the cord in crack, pulp spot, warp adhesion, thin warp, broken warp and weft. The defect recognition rate is 93%.

defect detection; mathematical morphology; support vector machines; tyre fabric

2016-07-03

国家自然科学基金项目(61304115)；河南省高校科技创新团队项目(14IRTSTHN024);河南省科技攻关项目(0721002210032)

温盛军(1979-)，男，福建宁化人，副教授，博士，主要研究方向为非线性控制、安全控制、机器人。

温盛军：博士，副教授，中原工学院青年拔尖人才，河南省高等学校青年骨干教师。2011年9月毕业于日本东京农工大学电子信息工程专业，获学术博士学位。主要研究方向为非线性控制、安全控制、机器人。承担和完成国家级科研项目3项、省部级科研项目5项、其他项目10余项，其中“基于Web的采暖与空调远程实时维护系统”项目获河南省科技进步三等奖，“毕业设计教学模式与质量监控体系的创新与实践”项目获河南省优秀教学成果一等奖。发表学术论文64篇，其中被SCI、EI收录43篇。

1671-6906(2016)04-0007-06

TP274

A

10.3969/j.issn.1671-6906.2016.04.002