基于星载可见光相机的空间碎片探测

赵　琪，翟　光

（北京理工大学，北京100081）

基于星载可见光相机的空间碎片探测

赵琪，翟光

（北京理工大学，北京100081）

空间碎片在轨识别与参数辨识为空间轨道预警、航天器规避空间碎片提供了重要依据。文章在轨道相对动力学的基础上，模拟了空间碎片在光学探测过程中的拖尾成像特性；随后，采用Hough变换对空间碎片尾迹特征进行提取与识别，获取碎片方位角信息，通过匹配多帧图像，获取碎片的方位角速度信息。同时，结合激光测距仪的测距信息，获取空间碎片的位置和速度信息；通过数值仿真验证，该方法能够实现对空间碎片探测、识别和定位，因而具有一定的工程应用价值。

图像模拟；拖尾；碎片识别；Hough变换；方位角计算

随着人类航天活动的快速发展，空间碎片带来的问题日益严峻。美国空间检测网站（SSN）数据显示，到2014年4月，地球轨道上已编目的尺寸大于10cm的空间物体达到16 655个[1]。尺寸在1～10cm的碎片约为6.7×105个，小于1cm的碎片超过200亿个[2]。随着人类航天活动的继续，空间碎片数量将继续增长。同时，碎片间的碰撞将产生更多小尺寸的新碎片[3-5]，根据已有空间碎片数据估算，未来空间碎片数目呈指数增长趋势[6-7]。为保护在轨正常运行的航天器，需要对空间碎片进行观测及定轨。

对于尺寸大于10cm的碎片，可通过地基雷达、望远镜等对其观测[8]，并对这些碎片进行编目，形成数据库，如德国的TIRA雷达、美国的Goldstone雷达、日本的MU雷达都具有较高探测精度[9]；对于小于1cm的碎片，可以采用在航天器舱壁外加装防护板的方法保护航天器[10]；对于1～10cm的碎片，受观测设备精度、地球曲率、大气层、天气、观测时间窗口等条件限制，地基观测的方式难以实现较高精度的观测与定轨。

与地基观测碎片不同，天基观测具有探测范围广、不受地球大气、天气等影响、覆盖范围广、探测精度高等优点[11-12]。目前，美国、欧洲、俄罗斯等国在天基监测技术方面已经取得了显著进展，如美国的“天基空间监视系统”（SBSS），该探测系统对近地轨道空间目标定轨误差约为10 m，高轨定轨误差500 m，并实现了24 h连续观测[13]。

本文采用可见光相机与激光测距仪对空间碎片进行天基观测，结合可见光相机的测角信息，驱动激光测距仪完成测距，实现对空间碎片的识别定位。

1　天基光学图像模拟

1.1碎片相对运动学

碎片的运动状态可以用相对运动方程来描述。若航天器轨道为圆轨道，可以采用C-W方程对碎片相对运动进行描述。

如图1所示，o-xyz为地心惯性坐标系（ECI），oo-xoyozo为航天器轨道坐标系，xo沿地心指向航天器质心方向；yo在轨道平面内指向航天器运动方向；zo与xo、yo构成右手直角坐标系。

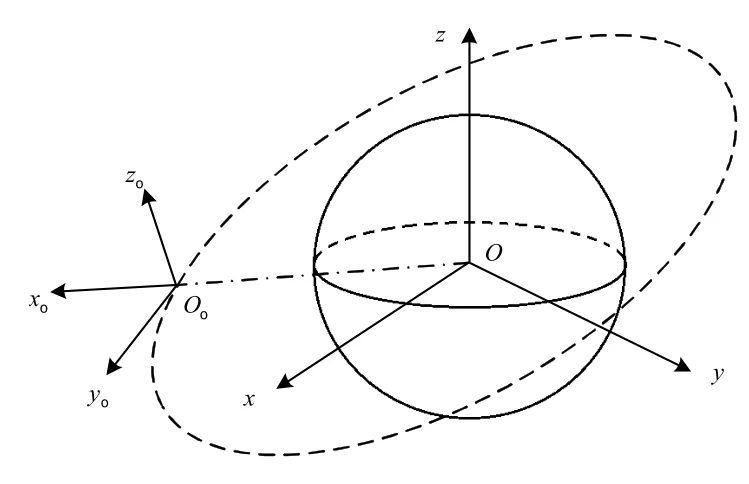
图1　轨道坐标系Fig.1 Orbital coordinate system

记rs与rt分别为航天器和碎片在ECI坐标系下相对地心的位置矢量，则航天器与碎片的轨道动力学方程为：

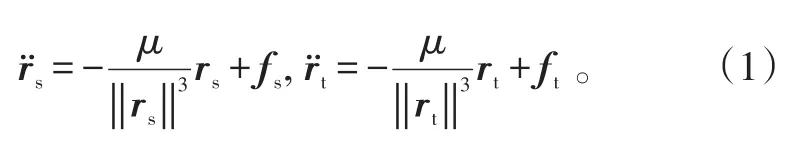
式（1）中：μ=398 600.44km3/s2为地球引力常数；fs与ft分别为除地心引力以外作用在航天器和碎片上的摄动力产生的摄动加速度。

碎片相对航天器位置矢量r为

将式（1）代入式（2），得：

根据坐标系间矢量微分法则，得式在航天器轨道坐标系下的表示式：

式中，ω与ω.分别为航天器的角速度与角加速度。

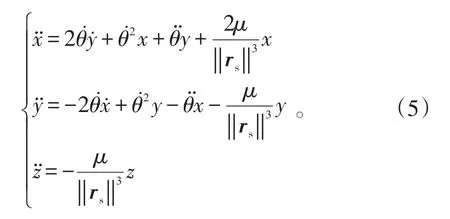
当航天器轨道为圆轨道时，有：

式（6）中：θ.为航天器运动角速度；θ为航天器运动角加速度。

将式（6）代入式（5），得：

式（7）即为C-W方程。给定初始条件，即可通过数值积分方法解得t时刻碎片相对运动状态。

1.2碎片拖尾特性

当碎片相对于航天器运动时，可能会导致碎片在积分时间（曝光时间）内在像平面上划过几个像素，形成拖尾。拖尾包含了碎片方位角、角速度信息。

记CCD相机面阵为m×m像素，曝光时间为tex，视场角为n°×n°，由此可得相机分辨率S为

所以，当碎片相对相机角速度超过S tex时，将在像平面上形成拖尾。

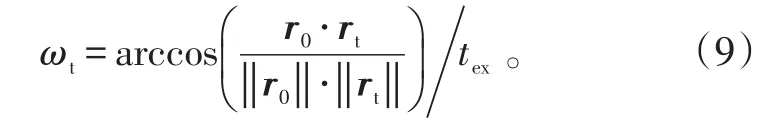
1.3碎片拖尾模拟

为模拟碎片拖尾，本文结合相机成像针孔模型对系统坐标系进行定义[14]。

图像物理坐标系 Op-XpYp、相机坐标系Oc-XcYcZc、世界坐标系Ow-XwYwZw示意图如图2所示。假设世界坐标系与相机坐标系重合，航天器轨道坐标系原点Oo与世界坐标系原点Ow重合；Zc指向航天器速度方向，Xc指向地心，Yc垂直于轨道面，与Xc、Zc构成右手直角坐标系。

图2　针孔成像原理Fig.2 Principle of pinhole imaging

图2中，f为相机焦距。假设世界坐标系与相机坐标系重合，轨道坐标系原点Oo与世界坐标系原点Ow重合，Zc指向航天器速度方向，Xc指向地心，Yc与Xc、Zc构成右手直角坐标系。

式（10）中，f为相机焦距。

在成像平面上定义如图3所示的数字图像坐标系o-uv，该坐标系以像素为单位，每个像素对应一个() u,v坐标，表示该像素在灰度矩阵中的列数与行数。

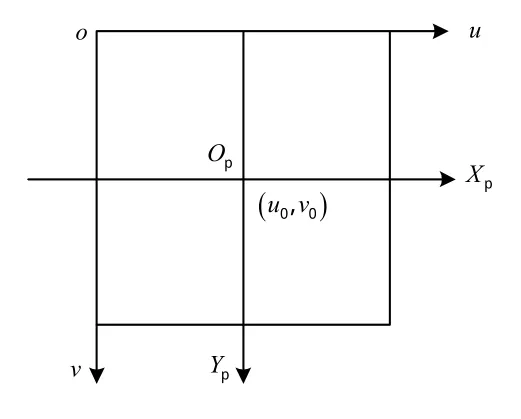
图3　(u,v)坐标系Fig.3(u,v)coordinate system

记每个像素在Xp与Yp方向上物理尺寸为dX、dY，CCD相机面阵为 m×m像素，取 u0=m 2，v0=m 2，得：

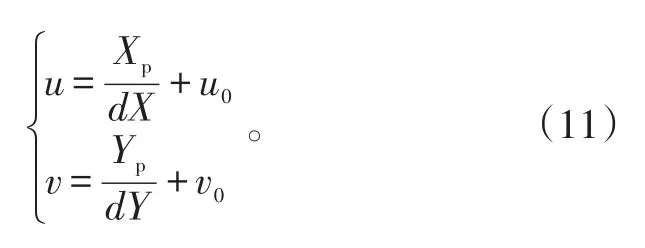
由于相机曝光时间短，拖尾可近似为一条直线。由初始运动状态及C-W方程，确定相机拍照帧初时刻与帧末时刻的位置矢量r0与rt，经坐标转换至世界坐标系，根据式（10）、（11），即可确定拖尾在相机所成像的首尾像素位置，将从而确定拖尾。之后，根据成像点在各个像素停留时间计算各个像素的灰度值。

2　拖尾目标识别

2.1边缘检测方法

Canny边缘检测算子是John F.Canny于1986年提出的一个多级边缘检测算法，是当前广泛使用的图像边缘检测算法[15-16]。

该方法先采用二维高斯函数沿任一方向的一阶方向导数与图像进行卷积滤波，之后在图像灰度矩阵中寻找灰度跃变位置，将这些跃变位置的点连起来，即得到图像边缘。

二维高斯函数表达式为：

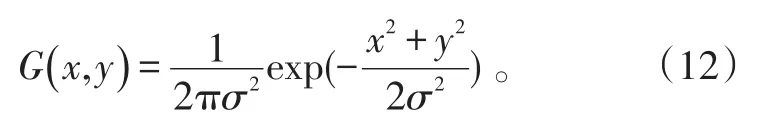
G(x,y)在方向n上的一阶方向导数为：

式（12）、（13）中：σ为高斯滤波器参数，控制滤波的平滑程度；为方向矢量。

改变方向矢量n，当Gn与图像 f() x,y的卷积取最大值时，对应的方向矢量正交于检测边缘的方向[17]。

对梯度幅值进行非极大值抑制，剔除伪边缘。剔除伪边缘后，使用双阈值算法检测和连接边缘。

2.2Hough变换检测直线

Hough变换于1962年由Paul Hough提出，其基本思想是运用参数空间进行坐标转换，并通过累计投票的方法得到最终检测结果。

为避免直线斜率无穷大的特殊情况，本文采用极坐标表示直线，其表达式为

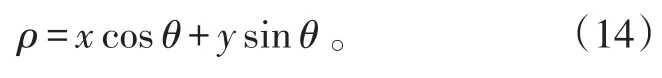
式（14）中：ρ为直线到原点的距离；θ决定直线斜率。

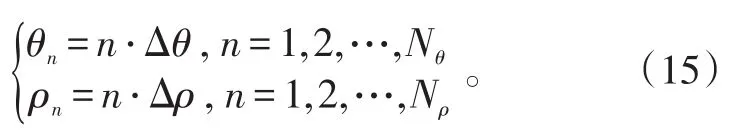
式（15）中：Nθ为参数θ的分割段数，Δθ=π Nθ；Nρ为参数ρ的分割段数；L为图像中距原点距离的最大值，Δρ=L Nρ。

Hough变换检测直线过程中，遍历图像上的每个像素点，当像素点灰度值满足特定要求时，找到所有经过该像素点的直线，并在这些直线对应的计数器上加1。当某条直线对应计数器的值大于设定的阈值K时，则认为在图像中存在该直线。

2.3拖尾直线检测

由于Hough变换检测直线的方法计算量较大，所以在Hough变换之前，首先采用Canny算子对拖尾轨迹进行边缘检测。之后，根据检测的结果，缩小检测范围。

如图4所示，灰色表示拖尾轨迹，虚线框表示Canny算子检测到的拖尾边缘。经边缘检测后，Hough变换的二维参数空间H() ρ,θ可以限制在边缘包含的区域内的直线，从而减小计算量。

图4　边缘检测示意图Fig.4 Schematic diagram of edge detect

3　拖尾目标方位角定位

3.1拖尾目标运动方向解算

如图4所示，图像中的拖尾轨迹存在2个端点，但1帧图像无法提供碎片运动的方向信息。因此，至少需要结合2帧图像才能解算出碎片相对航天器的角度信息。

首先，对第1帧图像中的拖尾轨迹进行检测，若存在拖尾，则计算拖尾的几何中心坐标。若第2帧图像中存在同一拖尾，则计算第2帧图像中拖尾的几何中心，几何中心计算方法为：

确定拖尾的平均几何中心后，通过相邻2帧图像拖尾的平均几何中心坐标即可得出碎片的运动方向。

3.2拖尾目标的帧间匹配

由于1帧图像中可能存在多个拖尾，所以在计算运动方向之前，需要进行帧间匹配对拖尾目标的身份进行验证。

以第1帧和第2帧图像为例，首先对第1帧图像进行处理，检测出所有拖尾，并记录所有拖尾的几何中心坐标、所在直线的参数；之后，对第2帧图像进行处理，比较2帧图像中拖尾所在直线的() ρ,θ参数，若所在直线参数之差小于设定的阈值，则可判定为同一碎片。此外，还可结合拖尾的灰度信息进行帧间匹配，提高匹配的鲁棒性。

同时，帧间匹配能在一定程度上减少噪声的干扰。随机噪声可能会产生类似于拖尾的轨迹，在目标检测时可能会被识别为拖尾目标。但由于噪声的随机特性，这种轨迹通过帧间匹配准则的概率很小。所以，经过帧间匹配之后类似于拖尾的噪声将被去除。

帧与帧之间拖尾匹配后，根据几何中心坐标计算碎片运动方向：

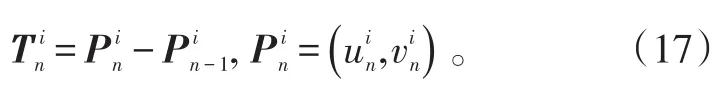
3.3方位角计算

根据碎片运动的方向信息，即可确定拖尾轨迹中曝光结束时刻碎片的位置。之后，即可求解碎片相对于相机的方位角。方位角示意图如图5所示。

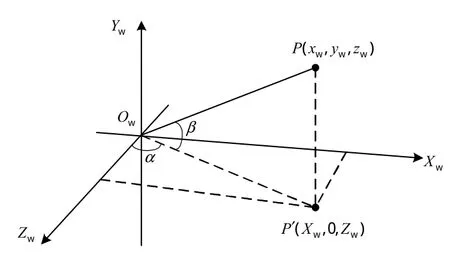
图5　方位角示意图Fig.5 Schematic diagram of azimuth angles

P′为碎片P在XwOwZw平面的投影。由方位角的定义，得方位角计算式为：

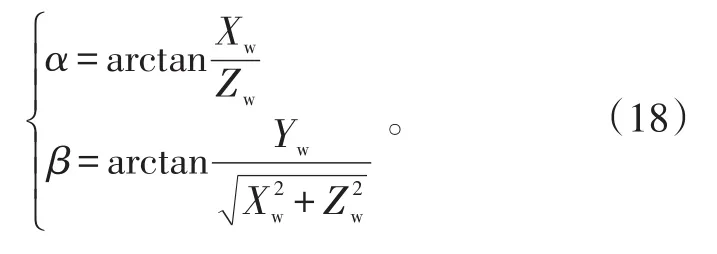
式（11）表示了图像坐标系Op-XpYp与数字图像坐标系o-uv的转换关系。根据坐标系间的关系，易得相机坐标系Oc-XcYcZc与图像坐标系Op-XpYp的转换关系为：

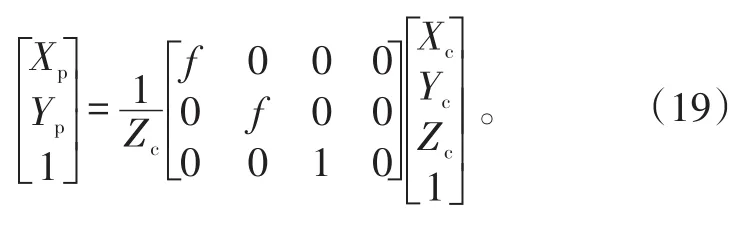
世界坐标系 Ow-XwYwZw与相机坐标系Oc-XcYcZc的转换关系为：

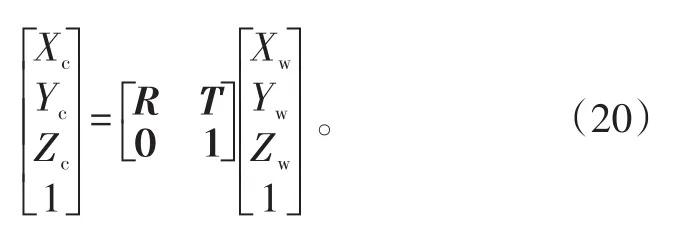
式（20）中：R为旋转矩阵；T为世界坐标系原点到相机坐标系原点的平移向量。

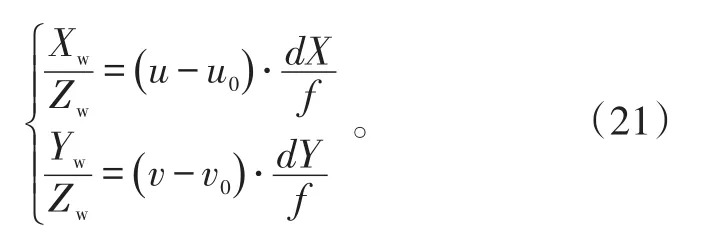
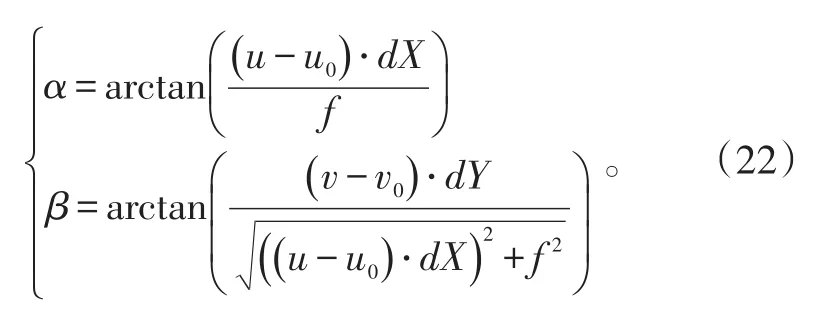
4　碎片运动状态重建

碎片拖尾提供了碎片的方位角、角速度信息。为了获得碎片的相对位置及相对速度，需要测量碎片相对航天器的距离。激光测距仪测距精度高，抗干扰能力强，体积小、质量轻，因而本文采用激光测距仪对碎片进行测距。

因激光测距仪视场角较小，故需使用电机驱动雷达指向碎片方位角。记电机接到指令到雷达开始测距耗时tr，若直接给电机发送拖尾末端的方位角，则可能导致雷达无法探测到碎片，因而需估算碎片在tr后的方位角。将相邻2帧图像中拖尾的质心坐标差分，即可解得碎片在o-uv坐标系下的速度，从而估算出tr后碎片的坐标。根据式（22），即可求得tr后碎片的方位角。之后，将估算的方位角发送到激光测距仪驱动电机，使激光测距仪提前指向该方位角。

连续2次获取碎片的位置信息进行差分，即可估算得到碎片的相对速度。根据碎片相对位置与相对速度，结合航天器轨道根数，即可获得碎片轨道根数。

5　仿真分析

假设航天器运行在GEO轨道，轨道偏心率e=0.000。星载可见光相机部分参数如表1所示。

表1　可见光相机参数Tab.1 Camera parameter

激光测距仪视场角为1°×1°，测距精度≤0.2 m，雷达驱动电机延时tr=0.06 s。碎片相对航天器运动初始状态如表2所示。

表2　碎片初始相对运动状态Tab.2 Initial relative motion state of debris

令碎片半径为10cm，相机成像灰度为50，由C-W方程及相机模型对碎片拖尾模拟，仿真步长取0.02 s，当t=0.16 s时，碎片拖尾如图6所示。

图6　碎片成像Fig.6 Debris imaging

对碎片相对运动状态进行重建，并与C-W方程数值解进行对比，结果如表3所示。t=0.04 s时，第2帧图像拍摄结束，获得拖尾方位角及运送方向信息；t=0.10 s时，激光测距仪完成第一次测距，获得碎片的位置信息；t=0.16 s时，激光测距仪完成第2次测距，获得第2个位置信息，与t=0.10 s时获得的碎片位置信息差分后，得到碎片速度信息。仿真结果表明，该方法能有效识别空间碎片，并对碎片运动状态的重建有较高精度。由于摄像机分辨率较低、碎片灰度值低、碎片距离较远等因素，导致对碎片运动状态的解算存在误差。工程上，可以通过提高摄像机分辨率、滤波等方法进一步提高碎片运动状态的识别精度。

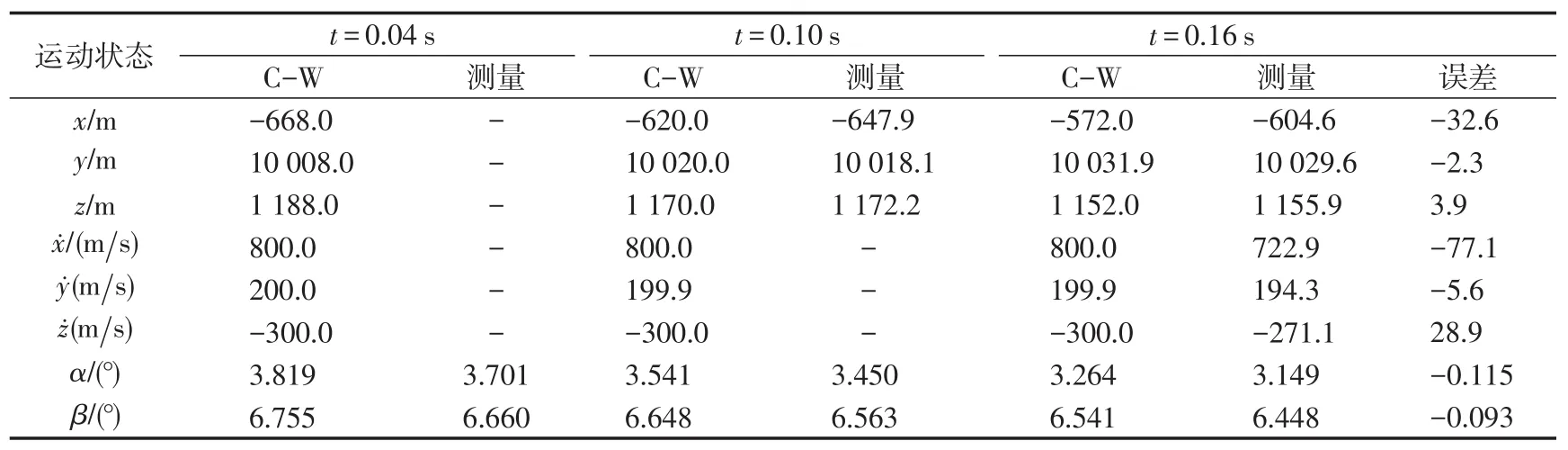
表3　C-W方程解算结果与图像-雷达测量结果对比Tab.3 Comparison of C-W function and measuring result of camera and radar

6　总结

本文根据碎片相对于航天器的C-W方程，结合针孔成像模型，对碎片拖尾进行模拟。在此基础上，结合边缘检测与直线检测方法，对碎片拖尾进行探测识别，解算出碎片方位角，结合激光测距仪测距，对碎片空间运动状态重建。通过数值仿真验证，该方法能有效识别空间碎片，并对其相对运动状态进行重建，具有一定工程应用价值。

[1]U.S.space surveillance network.monthly number of objects in earth orbit by object type[J/OL].Orbital Debris-Quarterly News，2014，18（1）：9-10.http：//www.orbitaldebris.jsc.nasa.gov.

[2]龚自正，徐坤博，牟永强，等.空间碎片环境现状与主动移除技术[J].航天器环境工程，2014，31（2）：129-135. GONG ZIZHENG，XU KUNBO，MU YONGQIANG，et al.The space debris environment and the active debris removal techniques[J].Spacecraft Environment Engineering，2014，31（2）：129-135.（in Chinese）

[3]KAPLAN M H.Survey of space debris reduction methods [C]//Proceedings of AIAA Space Conference&Exposition.AIAA，2009：14-17.

[4]SANG J，BENNETT J C，SMITH C H.Estimation of ballistic coefficients of low altitude debris objects from historical two line elements[J].Advances in Space Research，2013，52（1）：117-124.

[5]LIOU J C.An active debris removal parametric study for LEO environment remediation[J].Advances in Space Research，2011，47（11）：1865-1876.

[6]SMITH C H，GREENE B.Future space debris tracking requirements[C]//33rdAIAA International Communications Satellite Systems Conference and Exhibition.AIAA，2015：4361-4365.

[7]庞宝君，许可.空间碎片数据形式及轨道演化算法[J].上海航天，2011，28（1）：50-55. PANG BAOJUN，XU KE.Research on data format of space debris and orbit evolution algorithm[J].Aerospace Shanghai，2011，28（1）：50-55.（in Chinese）

[8]龚建村，刘四清，师立勤，等.空间环境天基探测现状与需求分析[J].空间科学学报，2009，29（3）：346-352. GONG JIANCUN，LIU SIQING，SHI LIQIN，et al.Status and demand analysis of space-based observation of space environment[J].Chinese Journal of Space Science，2009，29（3）：346-352.（in Chinese）

[9]ANZ-MEADOR P D，MATNEY M J，LIOU J C，et al.Updating the NASA debris engineering model：a review of source data and analytical techniques[J].Advances in Space Research，2001，28（9）：1391-1395.

[10]刘晓东.基于探测数据获取空间碎片轨道参数方法研究[D].哈尔滨：哈尔滨工业大学，2014. LIU XIAODONG.research on the method for obtaining the space debris orbit parameters based on detection data [D].Harbin：Harbin Institute of Technology，2014.（in Chinese）

[11]乔凯，王治乐，丛明煜.空间目标天基与地基监视系统对比分析[J].光学技术，2006，32（5）：744-746. QIAO KAI，WANG ZHILE，CONG MINGYU.Analysis on space based and ground based surveillance system to space target[J].Optical Technique，2006，32（5）：744-746.（in Chinese）

[12]SRIDHARAN R，PENSA A F.U.S.space surveillance network capabilities[C]//SPIE’s International Symposium on Optical Science，Engineering，and Instrumentation.International Society for Optics and Photonics，1998：88-100.

[13]周海银，潘晓刚，李董辉.基于天基空间目标监视系统的定轨技术研究[J].系统仿真学报，2008，20（13）：3538-3541，3547. ZHOU HAIYIN，PAN XIAOGANG，LI DONGHUI.Research on orbit determination algorithm based on SBSS [J].Journal of System Simulation，2008，20（13）：3538-3541，3547.（in Chinese）

[14]蔡晗，张景瑞，翟光，等.GEO非合作目标超近距相对位姿视觉测量[J].宇航学报，2015，36(6)：715-722. CAI HAN，ZHANG JINGRUI，ZHAI GUANG，et al.Relative pose determination for GEO non-cooperative spacecraft under the ultra-close distance[J].Journal of Astronautics，2015，36（6）：715-722.（in Chinese）

[15]CANNY J.A Computational approach to edge detection [J].IEEE Transactions on Pattern Analysis&Machine Intelligence，1986，8（6）：679-698.

[16]吕哲，王福利，常玉清.一种改进的Canny边缘检测算法[J].东北大学学报：自然科学版，2008，28（12）：1681-1684. LV ZHE，WANG FULI，CHANG YUQING.An improved canny algorithm for edge detection[J].Journal of North-eastern University：Natural Science，2008，28（12）：1681-1684.（in Chinese）

[17]余洪山，王耀南.一种改进型Canny边缘检测算法[J].计算机工程与应用，2004，40（20）：27-29. YU HONGSHAN，WANG YAONAN.An improved canny edge detection algorithm[J].Computer Engineering andApplications，2004，40（20）：27-29.（in Chinese）

[18]杨全银.基于Hough变换的图像形状特征检测[D].济南：山东大学，2009. YANG QUANYIN.Shape features detection based on hough transform in images[D].Jinan：Shandong University，2009.（in Chinese）

Space Debris Detection Method Based on Spaceborne Visible Camera

ZHAO Qi,ZHAI Guang
（Beijing Institute of Technology,Beijing 100081,China）

Detection and recognition of space debris provides a basis to the collision warning and maneuver strategy.In this paper,image tailing of space debris was simulated based on the C-W function.After that,the tailing was recognized by Hough transform method,the azimuth angles were calculated.By matching different images,the angular velocity was gotten.At the same time,the position and velocity of debris was obtained by combining the laser ranging information.Ac⁃cording to numerical simulation,this method was effective to detect,identify,and position debris,so it had good engineer⁃ing application prospect.

image simulation;tailing;debris recognition;Hough transform;azimuth angles calculation

V448.2

A

1673-1522（2016）01-0044-07

10.7682/j.issn.1673-1522.2016.01.009

2015-08-23；

2015-12-17

赵琪（1991-），男，硕士。