弹载共形相控阵天线拓扑结构分析

王　梅，胡志慧，张　君，尚　辉

（1.海军航空工程学院电子信息工程系，山东烟台264001；2.陆军航空兵学院，北京101123）

弹载共形相控阵天线拓扑结构分析

王梅1，胡志慧2，张君2，尚辉2

（1.海军航空工程学院电子信息工程系，山东烟台264001；2.陆军航空兵学院，北京101123）

以弹载多模复合制导雷达导引头为应用背景，在未考虑极化的情况下，首先建立了任意有向阵列的方向图函数；然后，采用同心圆等角度、同心圆等间距以及矩形栅格3种不同配置方式，建立了锥面共形相控阵天线模型，推导了不同配置方式下天线阵列方向图函数；通过比较其方位面及俯仰面的副瓣电平，得出结论：同心圆等间距配置方式是锥面共形相控阵雷达导引头天线单元的最优配置方式。

锥面共形相控阵天线；最优配置；导引头

随着精确制导技术的发展，传统单模导引头已不能满足现代作战的要求。多模复合导引头可兼顾主动与被动工作方式，已成为现代战争的有效途径。多模复合导引头须采用多个传感器，这给其天线设计带来了极大挑战。为满足设计要求，可以在共享一个头锥的情况下，将天线单元安装于导引头表面，从而形成共形相控阵天线[1-5]。共形相控阵天线是共形阵与相控阵的结合，不仅具有控制灵活、扫描速度快、扫描范围宽等优点，同时又具有隐身性能好、突防能力强等优点。因此，共形相控阵天线已成为新一代雷达导引头天线技术发展的重要方向[6-10]。

对于共形相控阵天线，各阵元位置及方向图指向都不同，因而不同的阵列配置方式对波束方向图有较大影响。文献[11-12]推导了有向共形天线单元从局部极坐标系到全局极坐标系的变换方法，并推导了锥面天线阵列的方向图函数，但这种方法需要天线单元方向图的极化信息，当极化信息未知时将不再适用。针对上述问题，本文以弹载多模复合制导雷达导引头为应用背景，在未考虑极化的情况下，首先建立了任意有向阵列的方向图函数；然后，采用同心圆等角度、同心圆等间距以及矩形栅格3种不同配置方式建立了锥面共形相控阵天线模型，推导了不同布阵方式下天线阵列方向图函数；通过比较不同方式下波束副瓣特性，确定了共形相控阵雷达导引头天线单元的最优配置方式。

1　任意有向阵列方向图函数

如图1所示，将N个天线单元安装于任一曲面上，假设第n个阵元的对应的三维坐标为(xn,yn,zn)，则其对应的位置矢量为：

图1　任意天线阵列方向图Fig.1 Direction map of arbitrary antenna array

假设ϕ、θ为目标方向上的方位角及俯仰角，则其单位向量为：

将坐标原点O作为相位参考点，则第n个阵元对应的相位差为：

假设在全局坐标系中第n个阵元的方向图函数为 fn(θ,ϕ)，则锥面共形相控阵天线的导向矢量为：

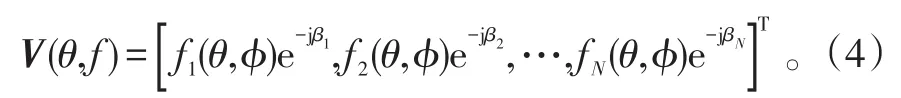
设期望信号(θT,ϕT)方向上的单位向量为

则在期望方向上的相位差为

假设第n个阵元的复加权矢量为

式（7）中：An为加权幅度；αn为加权相位。

锥面共形相控阵天线远场(θ,ϕ)的方向图为：

2　锥面共形相控阵天线阵列的配置方式

假设雷达运动平台如图2所示，其中锥角为θ0，圆台上底半径为R0，高为h，对于雷达下视角海面方向目标P对应的俯仰角及方位角为(θ,ϕ)。锥面共形相控阵天线单元布阵方式对阵列性能有着重要影响，为选择合理的布阵方式，分别采用同心圆等角度、同心圆等间距以及矩形栅格这3种方式对锥面共形相控阵天线进行了模型。

图2　雷达运动平台Fig.2 Platform of radar motion

2.1同心圆等角度配置方式

采用同心圆等角度配置方式时，共形相控阵天线阵列示意图如图3所示，天线阵列在xy平面内投影如图3 a）所示，整个天线阵列几何结构如图3 b）所示。由图3可知，从z轴方向观察，阵元沿锥台母线方向对齐排列，从xy平面观察，阵列可以看作是由若干个阵元数目相同的圆环子阵组成，每个阵元等间隔的分布在以与原点为起始角的圆环上。假设在z轴方向上等间距分布着M个圆环阵，圆环与圆环之间的垂直间距为dz，每个圆环上阵元间的角度间隔为Δϕ，单元数目为N=ceil(2π/Δϕ)，ceil为取整函数，第m个圆环的半径Rm=R0+(m-1)×dz×tan(θ0)。因此，阵列中第m个圆环上第n个阵元的位置为：

图3　同心圆等角度配置方式Fig.3 Configuration of concentric ring with equal angle

2.2同心圆等间距配置方式

共形相控阵天线阵列采用同心圆等间距配置方式如图4所示，图4 a）为天线阵列在xy平面内投影，图4 b）为整个天线阵列几何结构。由图4可知，阵列由M个圆环阵组成，圆环与圆环之间的垂直间距为dz，每个圆环上阵元按等间距de排列。第m个圆环半径 Rm=R0+(m-1)×dz×tan(θ0)，其 单 元 数 目 为N=ceil(2πRm/de)。因此，阵列中第m个圆环上第n个阵元的位置为：

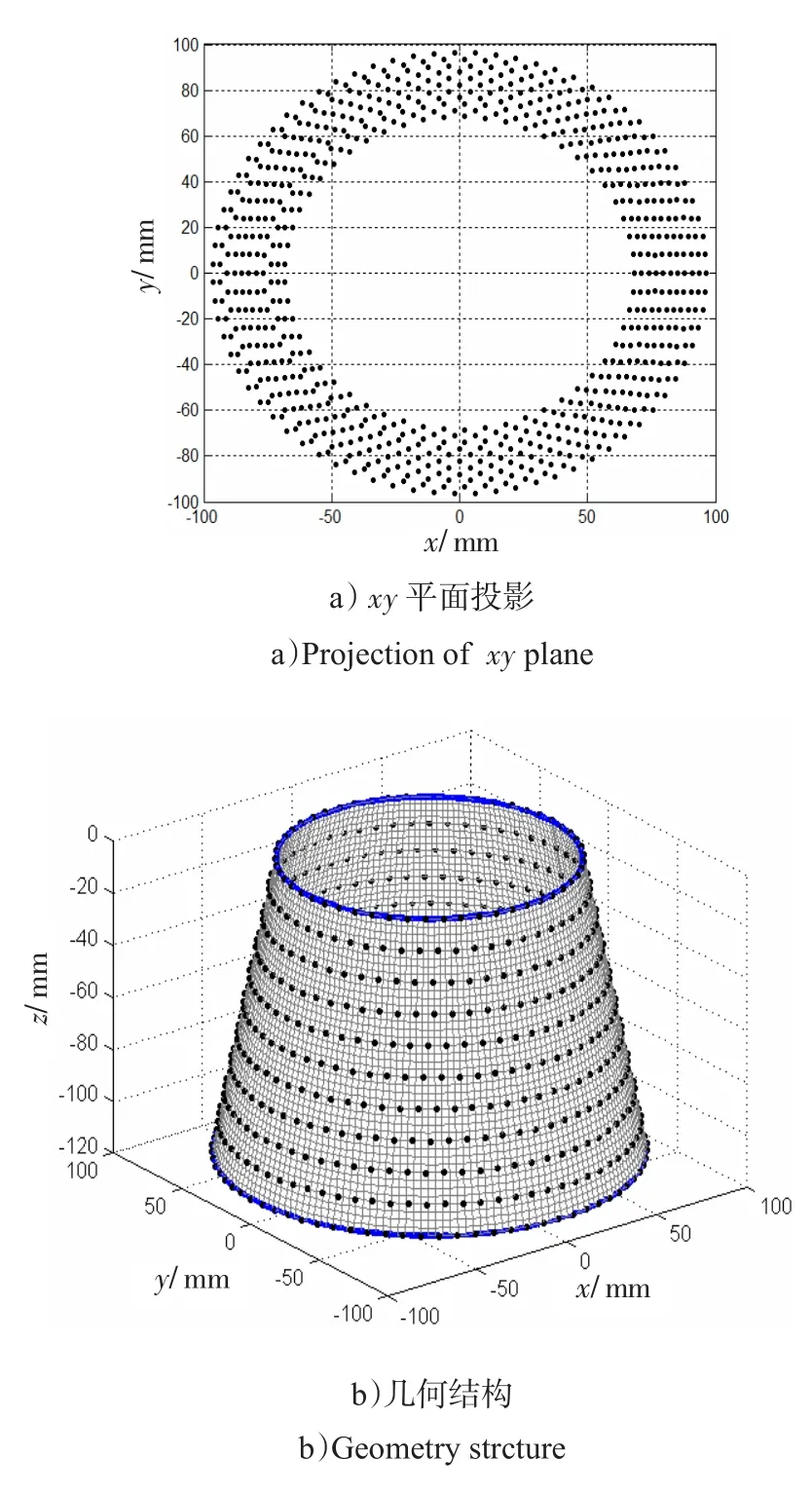
图4　同心圆等间距配置方式Fig.4 Configuration of concentric ring with equal distance

2.3矩形栅格配置方式

共形相控阵天线阵列采用矩形栅格配置方式如图5所示，图5 a）为天线阵列在xy平面内投影，图5 b）为整个天线阵列几何结构。由图5 a）可知，在xy平面内，阵列分布为矩形栅格，其在x及y方向上间距分别为Δx及Δy。

图5　矩形栅格配置方式Fig.5 Configuration of rectangular gird

从xy平面观察，第m行第n列所在阵元的位置为：

3　仿真及性能分析

3.1共形天线单元

为实现共形天线阵列小型化，本文采用凹槽加载的中心馈电方式设计了共形微带天线单元，如图6 a）所示。这种馈电方式可通过调整凹槽深度实现天线输入阻抗与微带馈线的阻抗匹配，实现起来简单易行，节省空间。天线工作在中心频率时，其俯仰面及方位面方向图如图6 b）所示，由图可知其最大增益为7.8dB，E面半功率波束宽度为±40°，H面波束宽度为±38°，E面及H面的后向辐射均小于-10dB。由此可知该天线单元方向图均匀、后瓣较小、结构紧凑、易加工制作于弹体，适用于构建弹载共形相控阵天线。

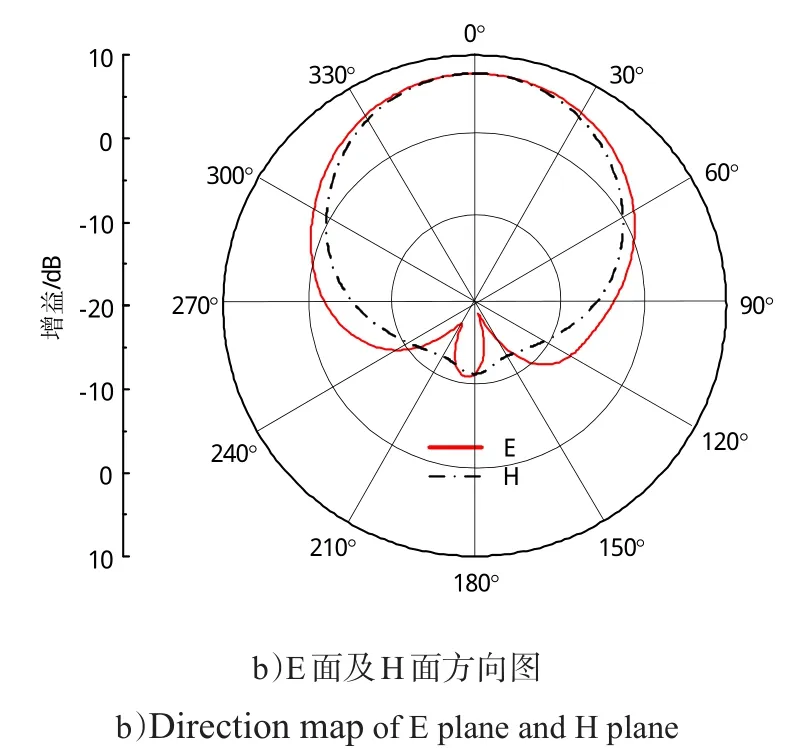
图6　共形天线单元Fig.6 Conical conformal antenna

3.2不同布阵方式下性能比较

本文以弹载多模复合制导雷达导引头为应用背景，假设锥台体高h=13λ，顶部半径R0=8.5λ，锥角θ0=14°，其中，心频率为35 GHz，阵元按上述3种配置方式分布于锥台表面。

假设阵列一为同心圆等角度配置方式，阵列由M=21个圆环阵组成，圆环与圆环之间的垂直间距为dz=0.65λ，每个圆环上阵元间的角度间隔为Δϕ=3.5°。

假设阵列二为同心圆等间距配置方式，阵列由M=21个圆环阵组成，圆环与圆环之间的垂直间距为dz=0.65λ，每个圆环上阵元按等间距排列，阵元间距为de=0.6λ。

假设阵列三为矩形栅格配置方式，其在x及y方向上间距分别为Δx=Δy=0.32λ。

天线单元共形于锥台表面，整个共形相控阵天线阵列被划分为多个子阵，为了实现大角度宽范围波束扫描，可在方位面采用子阵切换方式实现波束扫描，俯仰面采用相控扫描方式。假设每个子阵覆盖的方位角为90°，则阵列一、阵列二及阵列三在该子阵中所包含的阵元数目分别为525、535及519。为了确定了共形相控阵雷达导引头天线单元的最优布阵方式，分别对不同布阵方式下该子阵的波束性能进行了比较分析。

假设波束指向为锥面法向方向（76°,0°），阵列一、阵列二及阵列三在方位面及俯仰面的波束方向图分别如图7 a）、b）所示。由图7可知，不同布阵方式下3种阵列在方位面及俯仰面上其主瓣性能变化较小。但在方位面上副瓣区域，阵列二与阵列三其副瓣较低，阵列一在±90°附近其副瓣电平明显比阵列二及阵列三高。在俯仰面上副瓣区域，阵列一与阵列二其副瓣较低，阵列三在靠近锥角以及其后向附近其副瓣电平明显比阵列一及阵列二高。通过比较可知，同心圆等间距配置方式为锥面共形相控阵天线的最优配置方式。

图7　不同配置方式下性能比较Fig.7 Comparison with different topology

4　结论

本文以弹载多模复合制导雷达导引头为应用背景，首先建立了任意有向阵列的方向图函数；然后，采用同心圆等角度、同心圆等间距以及矩形栅格3种不同配置方式建立了锥面共形相控阵天线模型，推导了不同配置方式下天线阵列方向图函数；通过比较不同配置方式下方位面及俯仰面的副瓣电平，得出同心圆等间距配置方式是锥面共形相控阵雷达导引头天线单元的最优配置方式。

[1]JOSEFSSON L，PERSSON P.Conformal array antenna theory and design[M].Canada：Wiley Press，2006：1-2.

[2]YANG X S，QIAN H.Radiation pattern computation of pyramidal conformal antenna array with active element pattern technique[J].IEEE Antennas and Propagation Magazine，2011，53（1）：28-37.

[3]TANG W，ZHOU Y.Frequency invariant power pattern synthesis for arbitrary arrays via simulated annealing[J]. Electronics Letters，2010，46（25）：346-347.

[4]PERSSON P，JOSEFSSON L.Calculating the mutual coupling between antenna on a convex circular cylinder using a hybird UTD-MOM method[J].IEEE Transcations onAntennas and Propagation，2001，49（4）：672-677.

[5]OU YANG J，YUAN Q R，Yang F.Synthesis of conformal phased array with improved NSGA-II algorithm[J]. IEEE Transactions on Antennas and Propagation，2009，57（12）：4006-4009.

[6]YANG P，YANG F，NIE Z P.Robust beamformer using manifold separation technique for semispherical conformal array[J].IEEE Antennas and Wireless Propagation Letters，2011，10（2）：1035-1038.

[7]BUCCI O M，PINCHERA D.A generalized hybrid approach for the synthesis of uniform amplitude pencial beam ring arrays[J].IEEE Transactions on Antennas and Propagation，2012，60（1）：174-183.

[8]DESSOUKY M，SHARSHAR H，ALBAGORY Y.Efficient sidelobe reduction technique for small sized concentric circular arrays[J].Progress In Electromagnetics Research，2006，65：187-200.

[9]VILLEGAS F J.Parallel genetic algorithm optimization of shaped beam coverage areas using planar 2D phased array[J].IEEE Transactions on Antenna Propagation，2007，55（6）：1745-1753.

[10]KURUOGLU E E.Linear aperiodic array synthesis using an improved genetic algorithm[J].IEEE Transactions on Antenna Propagation，2012，60（2）：895-902.

[11]MORTON T E，PASALA K M.Performance analysis of conformal conical arrays for airborne vehicles[J].IEEE Transactions on Aerospace and Electronic Systems，2006，42（3）：876-890.

[12]HE Q Q，LIANG Y H，WANG B Z.Pattern synthesis and polarization optimization of a conical array[J].Journal of Electronic Science and Technology，2011，9（1）：71-77.

Topology Structure Analysis of Missile-Carried Conformal Phased Array

WANG Mei1,HU Zhihui2,ZHANG Jun2,SHANG Hui2
（1.Department of Electronic and Information Engineering,NAAU,Yantai Shandong 264001,China; 2.Army Aviation Institute,Beijing 101123,China）

Based on the application of seeker conformal phased array,a method of arbitrary conformal antenna pattern transformation from global coordinates to local coordinates was given firstly without the consideration of polarized informa⁃tion,and the expression of arbitrary array pattern was given.Then three different conical conformal array with the configu⁃ration of equal angle,equal distance and rectangular gird were modeled,the equal distance configuration was considered as the optimal configuration of conformal phased array seeker by the comparison of sidelobe of azimuth and elevation plane. Key words:conical conformal phased array;optimal configuration;missile seeker

TN82

A

1673-1522（2016）01-0034-05

10.7682/j.issn.1673-1522.2016.01.007

2015-11-10；

2015-12-23

山东省自然科学基金资助项目（ZR2012FQ004）

王梅（1983-），女，工程师，硕士。