基于优势粗糙集的证券投资决策研究及其应用

杨博翔

北京交通大学中国产业安全研究中心博士后科研工作站，北京100032

基于优势粗糙集的证券投资决策研究及其应用

杨博翔

北京交通大学中国产业安全研究中心博士后科研工作站，北京100032

粗糙集方法在金融及投资领域发挥着越来越大的作用，然而经典粗糙集理论不能发现偏好多属性决策表中与偏好属性相关的不相容性。本文基于优势粗糙集理论的知识约简算法，提出了基于优势关系的属性重要度约简算法，并构建了基于优势粗糙集的证券投资分析模型，针对中国上市公司财务数据为连续值、分布未知、含有偏好信息等特征，对证券样本进行综合排序，得到最终的综合排序和评价，并对算法进行有效性分析。

粗糙集；优势关系；证券投资决策

基于证券市场的全球化大背景，以及证券投资分析的重要作用，关于证券投资决策分析的理论和方法的研究已经成为一个重要的前沿领域［1］。以往的证券投资分析方法由于预测的精度比较低，或由于过于苛刻的基本假设而在真实市场中无法完全实现等问题，影响投资者进行科学、正确的投资决策。因此需要研究更适合于管理决策的数据挖掘方法——粗糙集方法。在一个投资决策方案中，偏好属性的顺序特性是很重要的决策信息，这就决定了优势粗糙集比传统的粗糙集理论对投资决策问题应具有更强的适应力和解释力［2］。

1　基于优势关系的属性重要度约简算法

将借鉴经典粗糙集启发式知识约简算法提出基于优势关系的偏好决策表的有效算法。属性约简是以获取最佳属性约简为目标的，前提条件是不损失原有信息系统的信息。在经典的约简算法中，最直观的就是使用删除法，但该复杂度非常高，不适合于数据和属性庞大的信息系统。为了降低复杂度，基于属性重要度的约简算法应运而生，经典的基于属性重要度的约简算法是建立在经典粗糙集理论的基础上的，因没有考虑到决策者的偏好决策需要，而使得约简结果容易产生不相容问题，大大制约了这种算法的使用。而在众多基于DRSA的知识约简算法中，以属性重要度为约简原则的算法还比较少。文章拟借鉴经典的基于属性重要度的约简算法，充分考虑偏好关系，以属性的重要性作为启发规则，寻求基于优势关系的启发式最小约简算法。基于优势关系的启发式最小约简算法的主要思想是，判断从条件属性集中删除某个属性后，剩下的条件属性集是否能将对象正确地划分到决策属性类中，最终找到与C的Cl分类质量一致的C的最小子集。

2　基于优势粗糙集的证券投资分析模型

2.1证券投资指标体系的选择与建立

2.1.1选择指标的原则一般来讲，选购股票就是选择上市公司。本文仅从证券投资者的角度出发，按照以下原则选择财务指标：

（1）由于不同行业在不同时期的情况不尽相同，如果选择多种行业的股票会导致对排序和评价的结果产生不良影响，使结果可信度不高，因此，选择一个行业板块进行股票指标的分析；

（2）考虑到指标的客观性、可比性原则，不选择反应公司经营规模和财务规模的指标，如资产总额、利润总额等，而是选择能够融合更多特征的指标，如每股净资产、股东权益等财务比率指标；

（3）选择指标要尽可能体现公司的财务结构、经营效率、成长能力、盈利能力、以及抵抗风险的能力，这些指标能够综合反映出公司的经营状况和财务状况，是进行投资选择的重要指标。

2.1.2证券投资指标体系的选择根据以上原则，在证券领域普遍认为的证券指标作为参照，确定以下9个证券投资财务指标：

（1）每股收益（元）=净利润/总股本；（2）每股净资产（元）=股东权益/总股本；（3）每股资本公积金=资本公积金/总股本；（4）每股未分配利润=未分配利润/总股本；（5）每股经营现金流量=经营活动产生的现金流量净额/总股本；（6）主营业务收入增长率（%）=（本期主营业务收入-上期主营业务收入）/上期主营业务收入；（7）净资产收益率=净利润/股东权益；（8）股东权益比=股东权益/资产总额；（9）资产负债率=负债总额/资产总额。

其中，指标1、2、3、4、5、7可以体现公司股票价值和盈利能力，指标6可以体系公司经营与发展能力，指标8可以反应公司财务结构，指标9可以反应公司抵抗风险的能力。

2.2针对偏好决策表的两种排序方法

2.2.1基于优势粗集权重的综合排序方法基于优势粗集权重的综合排序方法［3］的步骤：

（1）确定评价因素集C=｛C1，C2，...，Cn｝；

（2）确定评价目标集U=｛S1，S2，...，Sm｝；

（4）建立基于DRSA［4］的权重矩阵；

（6）多级综合排序：如果评价目标的有关因素很多，很难合理的定出权数分配，就难以真实的反映各因素在整体中的地位，有时通过一次综合排序很难分出评价等级，即评价次序，这时需要采取二级或多级评价。如综合二级评价。其中。这里算子“∧”，“∨”表示取大，取小的含义；

（7）综合评价。对综合排序结果向量进行分析。

以上基于优势粗集权重的综合排序方法的七个基本步骤，第四步和第七步为比较核心的两个步骤，第六步根据实际需要选取，也可不进行。由此，以优势粗糙集相关理论为基础，应用关系合成的原理，建立起基于优势粗集权重的综合排序方法。

2.2.2基于扩展Vague值理论的偏好决策表综合排序方法基于扩展Vague值的偏好决策表［5］综合排序方法的一般步骤：

（1）据（1）式将偏好决策表中的评价目标赋予扩展Vague值；

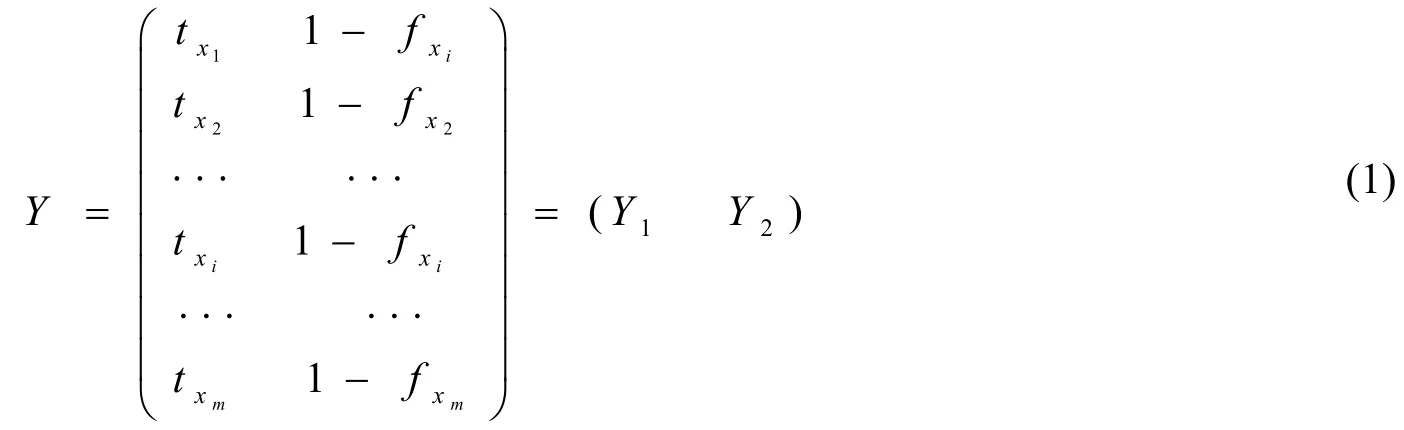
其中，tx表示基于优势关系扩展Vague集的肯定隶属度，fx表示基于优势关系扩展Vague集的否定隶属度为［6］；Yl是含有m个分量的一维列向量，l=1，2。

（2）根据扩展Vague值建立构造矩阵Y；（3）计算矩阵Y的最大特征值对应的特征向量作为排序向量；（4）根据排序向量对Vague值排序，分量越大，Vague值越大；（5）根据排序结果进行综合评价。

2.3基于优势粗糙集的证券投资分析模型

基于优势粗糙集的证券投资决策模型建立步骤：

（1）建立证券投资指标体系；（2）从证券网站上选数支股票为样本，输入各指标值并进行数据归一处理，生成初始偏好决策表；（3）将指标进行离散化，按照偏好顺序作分级处理，生成分级评价偏好决策表；（4）对决策表按照基于优势关系的属性重要度约简算法进行知识约简，得到约简后的偏好决策表；（5）按照两种综合排序方法对所选股票进行综合排序，得出评价结果，分析模型的有效性。

至此，证券投资决策模型构建完成。

3　应用研究

3.1样本选择及分析

本文从有色金属板块中随机抽取了35支股票2009年第四季度的数据作为研究样本，以9个财务指标作为条件属性，综合评价作为决策属性，由于这些属性均是含有偏好信息的，如投资者希望每股收益总是越高越好，资产负债率越低越好，决策属性也具有偏好信息，如评价等级越高，代表股票的质量越好，越值得投资，因此19家上市公司的财务数据便形成了一张初始的偏好决策表。从该偏好决策表中任意抽取3个属性，对其属性值的分布情况进行分析，发现属性的值域分布见图1。

图1所显示的是每股收益、主营收入增长率、股东权益比率三个属性指标的分布情况，可以看出，该三个属性指标均为无序分布，即不服从现有已知的正态分布、均匀分布等。

图1　证券指标属性值的分布Fig.1 Distribution of securities index properties

从以上属性的分布及其他属性的分布图中可知，各属性指标值的分布均不相同，对于该样本，首先对数据进行标准化处理，然后利用基于优势关系的属性重要度约简算法进行知识约简，得到约简后的偏好决策表，再利用综合排序方法对所选股票进行综合排序，得出最终的评价结果［7］。

3.2综合排序

3.2.1基于优势粗集权重的综合排序方法

由偏好决策表可知评价矩阵为R

综合评价模型

得到所选样本的综合排序为：

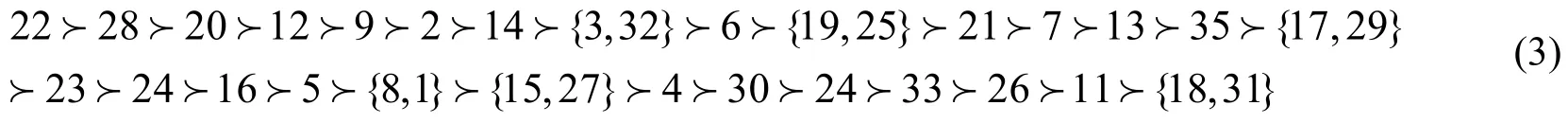
其中，“≻”代表优于，“｛｝”内元素表示评价值相同。

3.2.2基于扩展Vague值理论的偏好决策表综合排序方法基于优势关系扩展Vague集的肯定隶属度为

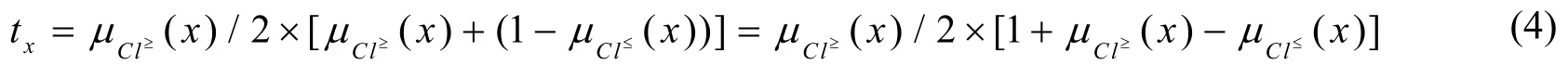
基于优势关系扩展Vague集的否定隶属度为

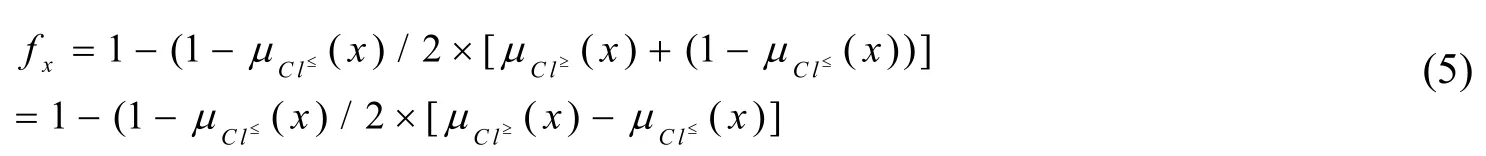
采用Eig函数［8］，用Matlab计算得：最大的特征值为：δ=24.7517。

得到所选样本的综合排序为：

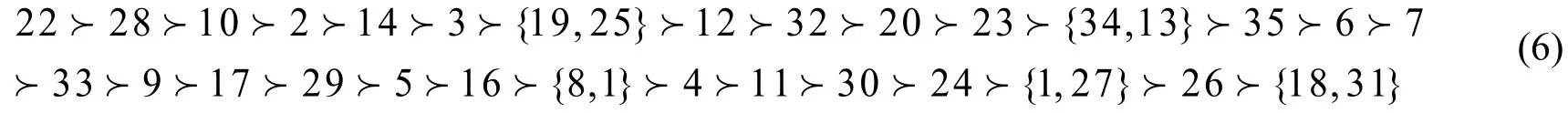
可见两种方法得到的产品排序有一定的差异，从ω的值可以看出第二种方法得出样本间的评价值非常接近，导致基于扩展Vague值理论的偏好决策表综合排序方法对样本数据分辨率不高，如果将精确度变低，将小数点后三位精确到小数点后两位，再看两种方法的综合排序结果。

基于优势粗集权重的综合排序方法：

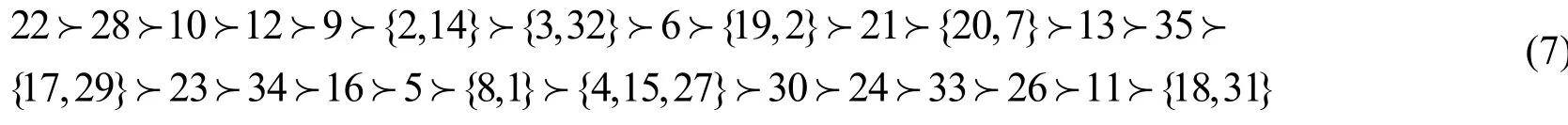
基于扩展Vague值理论的偏好决策表综合排序方法：

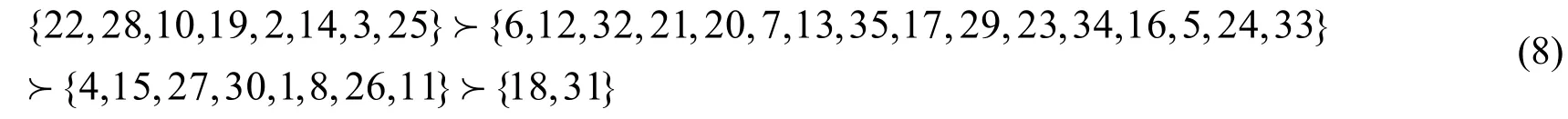
两种方法的排序结果的拟合度较高，排序结果基本相同。

3.3有效性分析

当结果取高精确度进行排序时，两种排序方法的结果有一定的差异性，主要是由于基于扩展Vague值理论的偏好决策表综合排序方法得出的评价值非常接近，对样本数据分辨率不高，但这时排名前两位和排名后两位的股票是相同的，可以告诉投资者者22、28两支股票评价值最高最值得推荐，18，31两支股票评价值最低要谨慎投资，同理，两种方法同样排名靠前的股票2综合评价值很高，股票26评价值都很低，模型不予推荐。

因此，当只关心综合评价最好的股票和综合评价最不好的股票时，模型是适用的，这种情况对投资者也是有意义的，因为投资者在投资时可能不需要全部的排序，只需挑出1到2支评价最高的股票进行投资，或者知道评价最低的股票，从而在投资时不予购买；当结果降低精确度进行排序时，两种排序方法的结果基本相同，上述案例中35个样本数据，排序相同的有27支股票，只有1、8、12、19、24、25、32、33等8支股票不同，两种方法的排序一致性达到77.14%，是一个满意的结果，对于8支“另类”样本，本文的模型可能不适应这类数据，对此将进行下一步研究。

4　结论

首先，构建了基于优势粗糙集的证券投资分析模型，提出了两种综合排序方法，给出了基于优势关系的偏好决策表的权重系数，并在此基础上给出了排序方法；利用上下联合的粗糙隶属函数基于优势关系扩展Vague集的肯定隶属度、否定隶属度，然后采用特征向量的方法，将不同的Vague区间值转化特征向量，建立了基于扩展Vague值理论的偏好决策表综合排序方法。根据上述研究，建立了基于优势粗糙集的证券投资分析模型的完整模型。最后，对所建立的基于优势关系的证券投资分析模型进行应用研究，并取得了良好的效果。

［1］曾剑锋，吴根秀.基于相异关系的粗糙集理论［J］.江西师范大学学报：自然科学版，2004，28（5）：426-430

［2］李钢，张雪婷.基于相似关系粗糙集的分解［J］.计算机工程与应用，2004（2）：85-87

［3］崔玉泉，张丽，史开泉.粗糙集的动态特性研究［J］.山东大学学报：理学版，2010，45（6）：8-14

［4］Ju S，Wu W，Zhang W.Approaches to Knowledge Reduction Based on Variable Precision Rough Set Model［J］. Information Sciences，2004（159）：255-272

［5］杨青山，王国胤，张清华，等.基于优势关系的区间值粗糙集扩充模型［J］.山东大学学报：理学版，2010，45（9）：7-13

［6］菅利荣，达庆利，陈伟达.基于粗糙集的不一致信息系统规则获取方法［J］.中国管理科学，2003，11（4）：90-95

［7］安利平，陈增强，袁著扯.多准则分级决策的扩展粗糙集方法［J］.系统工程学报，2004，12，19（6）：559-576

［8］侯福均，廖爱红，吴祈宗.判断信息为偏好序的社会选择：特征向量法［J］.南京理工大学学报：自然科学版，2008，32（12）：80-83

Research andApplication of Securities Investment Decision Based on Rough Set Theory

YANG Bo-xiang
Postdoctoral Scientific Research Workstation of China Center for Industrial Security Research/Beijing Jiaotong University，Beijing 100032，China

Rough set method plays a more and more important role in finance and investment field.However，the classical rough set theory cannot find the incompatibility between preference attribute and preference attribute in the decision table. Under this background，this paper constructed the dominance rough set based on securities investment analysis model and for the Chinese Listed Companies'financial data for continuous value，distribution is unknown，preference information and other characteristics，the comprehensive sort of sample securities was made and the final comprehensive ranking and evaluation were gotten to analyze the validity of the algorithm.

Rough set theory；dominance relation；security investment decisions

TN202

A

1000-2324（2016）05-0785-04

2016-05-15

2016-06-18

杨博翔（1989-），男，湖南常德人，博士后，主要研究方向为金融产业安全.E-mail：yangboxiang7@126.com