双树复小波和双谱在轴承故障诊断中的应用

侯少飞，李彦生，胥永刚，马朝永

（北京工业大学 机电学院 先进制造技术北京市重点实验室，北京 100124）

双树复小波和双谱在轴承故障诊断中的应用

侯少飞，李彦生，胥永刚，马朝永

（北京工业大学 机电学院 先进制造技术北京市重点实验室，北京 100124）

针对非线性、非平稳且包含强烈的噪声的轴承故障振动信号难以有效提取故障特征信息进行故障识别的问题，提出基于双树复小波变换和双谱的故障诊断方法。首先利用双树复小波变换将故障轴承振动信号分解为若干个不同频带的分量，选择出包含故障特征的分量；然后对该分量进行希尔伯特包络解调；最后对包络信号求其双谱图，从而有效地提取出故障信号的特征频率，准确地进行故障识别。滚动轴承故障实验和工程应用表明，该方法能有效地提取故障轴承的故障特征频率，并且几乎可以完全抑制噪声，验证了方法的可行性和有效性。

振动与波；双树复小波；双谱；希尔伯特包络；滚动轴承；故障诊断

旋转机械是电力、化工、冶金、和机械制造等重要工程领域中的关键设备［1］，滚动轴承作为旋转机械设备的重要组成部件［2］，同样也是易损坏的零件，而滚动轴承故障是导致机械设备运行过程中产生故障的主要原因之一。其中滚动轴承故障大多数发生在内圈与外圈上，其它故障则基本发生在滚动体上，很少有保持架发生故障［3］。轴承的运行状态将直接影响到整台机器的性能，因此对滚动轴承进行故障诊断具有非常重要的意义。然而实际工程中测得的滚动轴承振动信号通常表现出非线性、非平稳特征［4］，并且混有大量强噪声，很难有效地提取其故障特征信息，给滚动轴承故障诊断带来很大困难。如何从轴承的振动信号中提取相应的故障特征信息对诊断滚动轴承故障具有十分重要的意义［5］。

双树复小波变换最开始由Kingsbury等提出，后来经过学者Selesnick进一步发展并得以推广应用［6-7］。双树复小波变换保留了复小波变换的优良特性，而且采用双树滤波器的形式，保证了信号的完全重构性。因此，双树复小波变换是一种具有近似平移不变性、良好的方向选择性、有限的数据冗余性、完全重构性和计算效率高等良好特性的小波变换，已经成功应用于信号降噪处理［8］、故障诊断［9］等领域。

高阶谱分析技术是近年来信号处理的新技术，是分析非Gauss信号的良好工具。双谱是高阶谱中运算最简单且应用最广泛的分析方法，在理论上可完全抑制Gauss噪声的影响，识别信号中的二次相位耦合频率成分，适合分析非线性、非平稳信号，并且在轴承故障诊断中取得了成功的应用。轴承信号常表现为二次相位耦合模式，如轴承故障特征频率自身的耦合及故障特征频率与转频的耦合［10］。用双谱分析轴承振动信号更易获得故障特征信息。

本文提出基于双树复小波和双谱的滚动轴承故障诊断方法，并成功地将其应用于机械故障诊断。模拟实验和工程应用均表明，该方法可以有效地提取滚动轴承的故障特征频率，从而识别轴承的故障类型。

1　双树复小波的基本原理

双树复小波变换（dual-tree complex wavelet transform，DT-CWT）采用两个并行的实小波变换来实现信号的分解和重构，分别称为实部树和虚部树，DT-CWT的分解与重构过程如图1所示［6-7］。在信号的分解与重构过程中，始终保持虚部树的采样位置位于实部树的中间，使双树复小波变换能有效综合利用实部树和虚部树的小波分解系数，从而实现实部树和虚部树的信息互补。这种小波分解算法使双树复小波变换具有近似平移不变性，并减少了有用信息的丢失。双树复小波变换在各层的分解过程中，利用小波系数二分法减少了多余的计算，从而提高了计算速度。根据双树复小波的构造方法，复小波可表示为

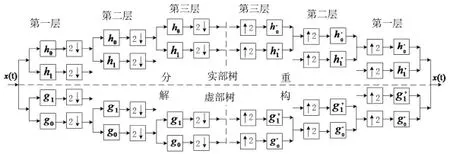
图1　双树复小波变换的分解和重构过程

式中ψh（t），ψg（t）表示两个实小波；i为复数单位。

由于双树复小波变换由两个并行的小波变换组成，因此，根据小波理论，上面实部树小波变换的小波系数和尺度系数可由式（2）和式（3）计算

同理，下面虚部树小波变换的小波系数和尺度系数可由式（4）和式（5）计算

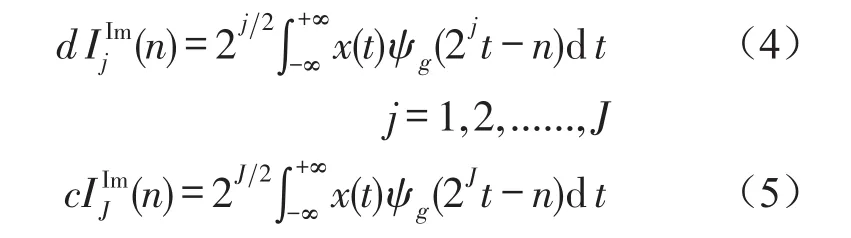
因此，可以得到双树复小波变换的小波系数和尺度系数

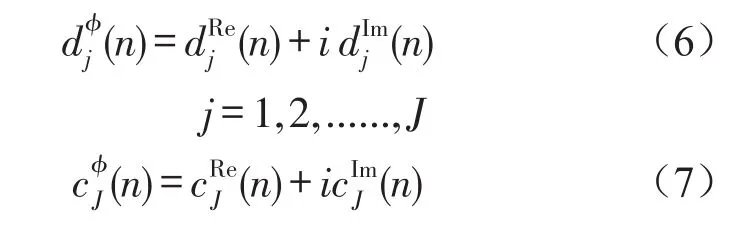
最后，双树复小波变换的小波系数和尺度系数可由式（8）和式（9）进行重构

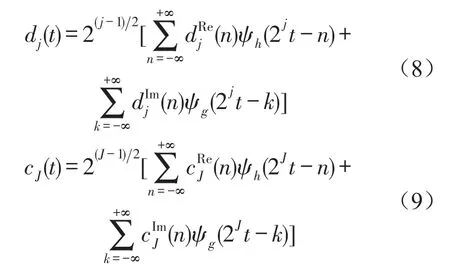
双树复小波变换后的重构信号可表示为

图1所示为3层双树复小波分解和重构过程，在分解过程中，h0、h1分别为实部树对应的低通滤波器和高通滤波器，g0、g1分别为虚部树对应的低通滤波器和高通滤波器。同样，在重构时，h0'、h1'为实部树滤波器组，g0'、g1'为虚部树滤波器组，本文采用Kingsbury所构造的Q-shift双树滤波器［7］。

2　双谱的基本原理

传统的自相关和功率谱方法只是利用了信号的2阶统计量信息，对于平稳、高斯过程，这已经能够反映信号的特征，但是对于实际的机械系统来讲，非线性、非平稳、非高斯过程更具有普通性和一般性，这就需要从更高的阶次上来反映信号特征。高阶谱是分析非高斯信号、非平稳、非线性系统的有力工具，有着广泛的应用。双谱在高阶谱方法中阶数最低，处理方法最简单，能够抑止高斯噪声，突出非高斯特征，所以在高阶谱方法中受到的关注最多，应用也最为广泛［11］。

零均值平稳随机信号 x（n）的3阶累积量d（τ1、τ2）定义为

式中τ1、τ2为时间延迟；E［∙］为统计均值。

双谱B（ω1、ω2）定义为3阶累积量d（τ1、τ2）的二维傅里叶变换，即

若x（n）是一个具有有限能量的确定性信号，则傅立叶变换、功率谱和双谱的定义分别如下

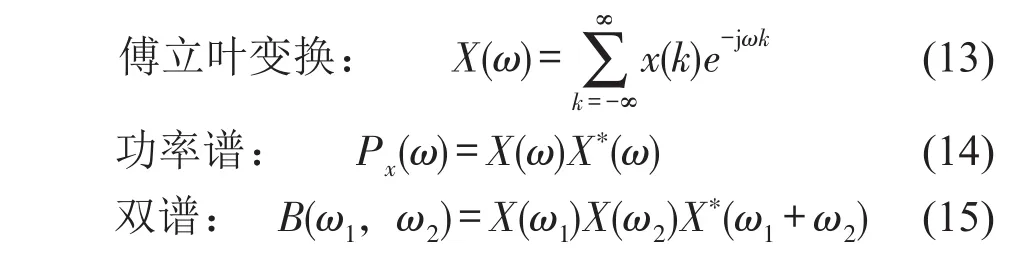
上式中“*”表示复共扼。

从该定义可以看出双谱为复数值，定义在由自变量ω1和ω2分别表示的两个频率轴f1和f2构成的二维平面上，包含相位信息。双谱B（ω1，ω2）的幅值表示频率分量ω1、ω2和ω1+ω2之间的耦合量。由故障轴承振动信号解调出的包络信号的频谱表现为由故障频率及其倍频组成的一系列等间隔的谱峰。假设f0为故障频率，则f0、2f0，…处均会出现峰值，这些谱峰即为故障模式。当ω1、ω2为故障频率或者其倍频，可知ω1+ω2也为故障频率或者其倍频，双谱图在（ω1、ω2）处将出现峰值。且B（ω1、ω2）将是ω1、ω2、ω1+ω2个故障相关频率共同作用结果，其值得到明显增强。而其他位置的频率点则没有这种效果，受到抑制。因此双谱能够增强故障特征频率，抑制噪声频率干扰，比功率谱更适合分析由故障振动信号解调得到的包络信号［12］。

3　双树复小波和双谱的诊断方法

其诊断具体步骤如下：

（1）对故障轴承振动信号进行双树复小波分解，得到几个不同频段的分量。

（2）选择出包含故障特征的分量；然后对包含故障特征的分量进行希尔伯特包络解调。

（3）最后对包络信号求其双谱图，从而有效地提取出故障信号的频率特征，便能准确地识别故障类型，实现故障诊断。

4　实验分析

实验系统由轴承故障模拟实验台、笔记本电脑和HG 3604故障诊断仪组成。轴承故障模拟实验台如图2所示。

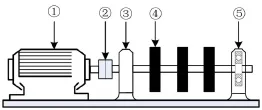
图2　轴承故障模拟实验台

由两个6307深沟球滚动轴承支撑，通过挠性联轴器与电机相连。在靠近电机侧安装正常轴承（即图2中③），远离电机侧安装故障轴承（即图2中⑤），用于模拟各种轴承故障。实验中，利用HG 3604故障诊断仪在故障轴承所在的轴承座测取振动加速度信号。故障轴承的型号为6307，轴承的大径D=80 mm，小径d=35 mm，滚动体个数为8个，压力角α=0，故障类型为裂纹，故障大小为一条宽0.5 mm，深0.5 mm的槽模拟裂纹故障，实验台转速1 496 r/min，对采集到的轴承故障数据进行分析采样点数是8 192，采样频率15 360 Hz，根据上述参数经过公式计算得到转频为24.933 3 Hz，轴承外、内圈故障特征频率为76.728 Hz、122.738 Hz。

4.1轴承外圈故障诊断

图3为轴承外圈裂纹故障的时域波形及其幅值谱，从时域波形可以看出原始信号中确实存在冲击性成分，但周期性不是很明显。幅值谱中亦出现了边频带成分，同时也存在强烈的干扰成分，无法根据波形及频谱有效识别故障。

故利用双树复小波对原始信号进行4层分解，然后进行重构，得到如图4所示的重构信号a4、d4、d3、d2和d1，各重构信号对应的幅值谱如图5所示。

根据双树复小波分解原理可知，各重构信号对应的频率范围分别为a4（0～480 Hz）、d4（480 Hz～960 Hz）、d3（960 Hz～1 920 Hz）、d2（1 920 Hz～3 840 Hz）和d1（3 840 Hz～7 680 Hz），从图3的幅值谱中可以看到在1 000 Hz～2 000 Hz之间存在边频带成分，与之对应的是图5中的第三个分量d3。

故将第三个分量d3作为研究对象，d3分量对应的幅值谱如图5所示。可以从图5中看到明显的边频成分，但是还存在一定的噪声干扰。故直接对d3分量做包络解调，然后求其双谱，得到双谱等高线图，如图6所示。

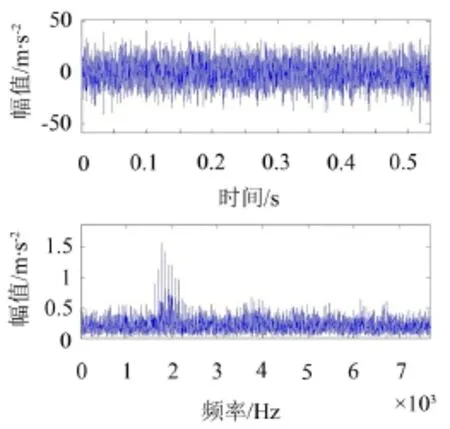
图3　轴承外圈裂纹故障的时域波形及幅值谱

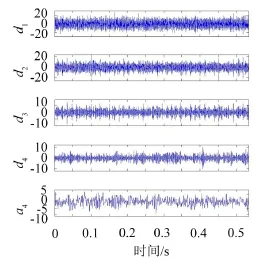
图4　外圈故障双树复小波重构信号时域波形

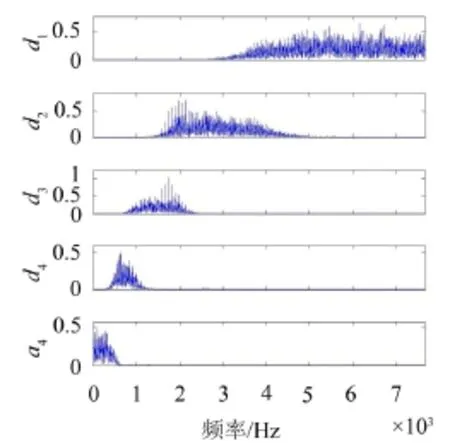
图5　外圈故障双树复小波重构信号的幅值谱

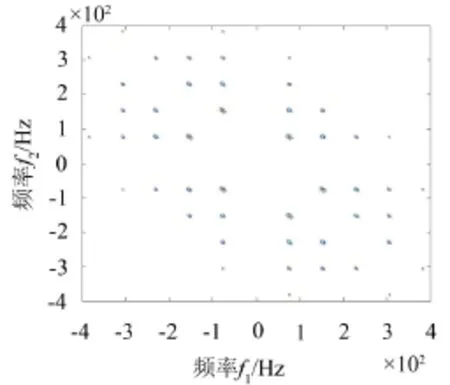
图6　d3分量包络后的双谱等高线图

从图6中可以清楚地看到（76.88、76.88）、（76.88、153.8）、（153.8、76.88）等处出现峰值，这与理论计算的外圈故障特征频率76.728 Hz及其倍频十分接近，由此可以断定此轴承外圈发生了故障，与模拟故障相符，证明了该方法的有效性。

4.2轴承内圈故障诊断

图7为轴承内圈裂纹故障的时域波形及其幅值谱，从时域波形可以看出原始信号中确实存在冲击性成分，但周期性不是很明显。幅值谱中亦出现了边频带成分，同时也存在强烈的干扰成分，无法根据波形及频谱有效识别故障。

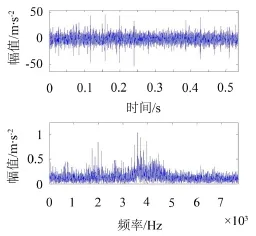
图7　轴承内圈裂纹故障的时域波形及幅值谱

故利用双树复小波对原始信号进行4层分解，然后进行重构，得到如图8所示的各层重构信号a4、d4、d3、d2和d1，各重构信号对应的幅值谱如图9所示，各重构信号对应的频率范围分别为a4（0～480 Hz）、d4（480 Hz～960 Hz）、d3（960 Hz～1 920 Hz）、d2（1 920 Hz～3 840 Hz）和d1（3 840 Hz～7 680 Hz）。同理，从图7的幅值谱中可以看到在2 000 Hz～4 000 Hz存在边频带成分，与这个频段相对应的分量是图9中的第二个分量d2。

故将第二个分量d2作为研究对象，d2分量对应的幅值谱如图9所示。

可以从图9中明显地看到边频成分，但是还存在一定的噪声干扰。故直接对d2分量做包络解调，然后求其双谱，得到双谱等高线图，如图10所示。

可以清楚地看到（121.9、121.9）、（121.9、245.6）、（245.6、121.9）等处出现峰值，这与理论计算的外圈故障特征频率121.9 Hz及其倍频十分的接近，由此可以断定此轴承外圈发生了故障，与模拟故障相符，证明了该方法的有效性。

图8　内圈故障双树复小波重构信号时域波形

图9　内圈故障双树复小波重构信号的幅值谱

图10　d2分量包络后的双谱等高线图

5　工程案例

某钢厂的二高线精轧机增速箱出现了问题，故障位置为增速箱II轴上型号为162250D的轴承，轴承外圈出现断裂故障，断裂的轴承外圈如图11所示。

图11　轴承外圈断裂

事故发生时该设备的转速为1 169 r/min，采样频率为10 000 Hz，采样点数为2 048。根据轴承故障频率计算公式得到外圈故障特征频率为503.25 Hz。早期故障数据的时域波形图及其幅值谱如图12所示。

图12　工程信号的时域波形及幅值谱

从时域波形和幅值谱中我们无法得到有用的信息，无法准确识别故障轴承对应的特征频率。

利用双树复小波对原始信号进行4层分解，然后进行重构，得到如图13所示的各层重构信号a4、d4、d3、d2和d1，对应幅值谱如图14所示，各重构信号对应的频率范围分别为a4（0～312.5 Hz）、d4（312.5 Hz～625 Hz）、d3（625 Hz～1 250 Hz）、d2（1 250 Hz～2 500 Hz）和d1（2 500 Hz～5 000 Hz）。同理，从图12的幅值谱中可以看到在1 000 Hz～2 500 Hz存在边频带成分，与这个频段相对应的分量是图14中的第二个分量d2。

选择选择第二个分量d2作为研究对象，d2分量对应的幅值谱如图14所示，从图中可以看到边频成分并不明显，同时还存在一定的噪声干扰。故直接对d2分量做包络解调，然后求其双谱，得到双谱等高线图，如图15所示。

从图15中，可以清楚地看到（502.9、502.9）、（502.9、1006）、（1006，502.9）等处出现峰值，这与理论计算的外圈故障特征频率503.25 Hz及其倍频十分的接近，由此可以断定此轴承外圈发生了故障，这与拆箱检查的结果相符，证明了该方法的可行性和有效性。

图13　工程信号双树复小波重构信号时域波形

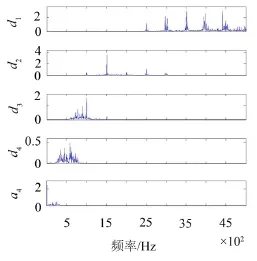
图14　工程信号双树复小波重构信号幅值谱

图15　d2分量包络后的双谱等高线图

6　结语

本文对双树复小波和双谱的滚动轴承的故障诊断进行了研究，通过滚动轴承故障实验和工程应用验证了方法的有效性。

（1）对轴承故障振动信号进行双树复小波分解和重构，得到几个不同频段的分量。选择出包含有故障特征的分量。既保留了信号中的有用成分，又达到了一定的降噪效果，再对含有故障特征的分量进行双谱分析，双谱能够抑止高斯噪声，突出非高斯特征，可以有效地提取故障信号中冲击成分，得到故障特征频率，进行故障诊断。

（2）将双树复小波和双谱应用于滚动轴承的故障诊断中，可以有效和准确地提取故障特征信息并且几乎可以完全抑制噪声，从而实现轴承的故障诊断。

［1］刘继承，聂品磊，佟宇.基于形态滤波和EMD-AR谱的轴承故障特征提取［J］.噪声与振动控制，2015，35（3）：159-162.

［2］刘尚坤，唐贵基.自适应MED结合EMD诊断滚动轴承早期故障［J］.噪声与振动控制，2015，35（6）：159-162.

［3］陈志新.对偶树复小波分析及其在故障诊断中的应用［D］.北京：北京科技大学，2007.

［4］钟先友，曾良才，赵春华.局域均值分解和1.5维谱在机械故障诊断中的应用［J］.中国机械工程，2013，24（4）：452-457.

［5］冯志鹏，刘立，张文明，等.基于小波时频框架分解方法的滚动轴承故障诊断［J］.振动与冲击，2008，27（2）：110-114.

［6］KINGSBURY N G.The dual-tree complex wavelet transform:a new technique for shift invariance and directional filters［J］.IEEE Digital Signal Processing Workshop，1998.

［7］SELESNICK I W，BARANIUK R G，KINGSBURY N G. The dual-tree Complex wavelet transform［J］.IEEE Digital Signal Processing Magazine，2005，22（6）:123-151.

［8］陈志新，徐金梧，杨德斌.基于复小波块阈值的降噪方法及其在机械故障诊断中的应用［J］.机械工程学报，2007，43（6）：200-204.

［9］吴定海，张培林，任国全.基于双树复小波包的发动机动信号特征提取研究［J］.振动与冲击，2010，29（4）：160-163.

［10］唐贵基，庞彬.基于ITD和切片双谱的滚动轴承局部损伤故障诊断［J］.轴承，2014（8）：43-47.

［11］李中原.旋转机械矢双谱分析及故障诊断应用研究［D］.郑州：郑州大学，2006.

［12］郑红，周雷，杨浩.基于谱峭度与双谱的轴承故障诊断方法［J］.北京航空航天学报，2014，40（9）：1176-1182.

Applications of Dual-tree Complex Wavelet Transform and Bi-spectrum in Roller Bearing Fault Diagnosis

HOU Shao-fei，LI Yan-sheng，XU Yong-gang，MA Chao-yong
（College of Mechanical Engineering andApplied Electronics Technology，Key Laboratory ofAdvanced Manufacturing Technology，Beijing University of Technology，Beijing 100124，China）

It is difficult to extract fault characteristic signals from the nonlinear，non-stationary and strong noise included fault vibration signals of roller bearings for fault identification.In this paper，a new fault diagnosis method is proposed based on dual-tree complex wavelet transform（DT-CWT）and bi-spectrum.Firstly，the fault vibration signal is decomposed into several components with different frequency-band through DT-CWT，and the components which contain the fault feature information are selected.Then，the Hilbert envelope demodulation is used to the components.Finally，the bispectrum diagram of the envelop signals is acquired and the fault signal frequency feature can be effectively extracted to identify the fault accurately.The results of the roller bearing fault tests and engineering application show that the fault feature frequency of the fault roller bearing in operation can be extracted accurately by this method and the noise can be almost completely suppressed.Thus，the feasibility and effectiveness of this method are verified.

vibration and wave；dual-tree complex wavelet transform；bi-spectrum；Hilbert envelope；rolling bearing；fault diagnosis

TH133.3；TH165

ADOI编码：10.3969/j.issn.1006-1335.2016.05.028

1006-1355（2016）05-0133-06

2016-03-11

国家自然科学基金资助项目（51375020）；北京市教委科研计划资助项目（KM201310005013）

侯少飞（1988-），男，河北省邢台市人，硕士研究生，主要研究方向为机电设备状态监测与故障诊断。

胥永刚（1975-），男，河北省定州市人，博士，副教授。E-mail:xyg@bjut.edu.cn