探测器月面起飞稳定性边界条件研究
胡建国,史耀祖,赵毅,徐宏斌
西安现代控制技术研究所,西安 710065
探测器月面起飞稳定性边界条件研究
胡建国*,史耀祖,赵毅,徐宏斌
西安现代控制技术研究所,西安 710065
探测器起飞稳定性是上升器月面起飞的重要性能指标,研究其特性对上升器返回地面具有重要的意义。选择上升器起飞稳定性主要影响因素,结合优化拉丁超立方试验设计方法和径向基神经网络建立了上升器起飞过程动力学近似模型,定量地判定出姿态角位移、姿态角速度对各影响因素的敏感程度。以上升器的姿态角位移和角速度分别为5°和5(°)/s为稳定判定条件,给出了单个影响因素的取值边界。编写了上升器起飞稳定性多因素边界条件分析程序,采用三维空间的方式建立了上升器起飞稳定性边界条件表达式,并以样例确定了起飞稳定性边界条件。
航天器结构与设计;月球探测器;起飞稳定性;近似模型;敏感度;临界条件;综合判据
探测器起飞稳定性是指探测器月面起飞过程中能否保持合理的姿态,是上升器月面起飞的重要性能指标,直接关系到探月任务的成败。探测器系统的稳定性主要包括探测器着陆过程的稳定性和上升器月面起飞的稳定性。
国内外已有大量文献[1-5]对探测器着陆过程动力学和着陆稳定性进行分析和研究,而上升器上升入轨段的研究很少,且都集中在对上升轨迹的优化[6-9],缺少对上升器起飞稳定性和可靠性的影响因素进行分析和研究。
由于探测器的结构制造与安装误差,以及着陆姿态的不确定性,导致针对某个具体的探测器,其起飞稳定性状况也不一样。本文在起飞稳定性主要影响因素的基础上,结合试验设计方法和有限元仿真结果建立了起飞动力学近似模型,并进行了有效性验证;然后,利用近似模型采用多元回归的方法分析了起飞稳定性对各影响因素的敏感度;最后以探测器姿态角和角位移为目标,建立上升器起飞稳定性评估模型,编写了起飞稳定性多因素边界条件分析程序,并给出了单因素边界和多因素综合判据。研究结果可为探测器设计和月面起飞稳定性评估提供理论依据。
1 探测器模型
探测器主要由上升器(箱体式结构本体、球形燃料贮箱、主推力发动机、上升器桁架、姿控发动机与太阳翼),着陆器(箱体式结构本体、着陆缓冲机构、足垫)以及过渡段等组成。上升器通过上升器桁架与过渡段的导轨配合,过渡段导轨固定在着陆器上,着陆器通过万向节与主辅缓冲器相连接,主辅缓冲器实现能量缓冲及支撑上升器起飞作用。根据实际结构作适当的简化,建立探测器有限元模型,如图1所示。

图1 探测器模型Fig.1 Lunar detector model
2 起飞稳定性主要影响因素
根据经验分析,上升器起飞稳定性的影响因素主要包括上升器和着陆器的质量特性、上升器起飞主发动机推力特性、羽流力效应、外扰力特性、着陆缓冲机构特性、过渡段、探测器着陆后姿态和着陆场坪条件等;根据现有研究[10-11]设计技术要求以及经验综合分析这些影响因素,选择一些主要的影响因素,具体因素及其设计范围如表1所示。

表1 起飞稳定性主要影响因素及其设计范围
表中:XWH-H为限位环高度;ZTJ为着陆器着陆后姿态角;TL-Y、TL-Z为主发动机Y、Z方向推力作用点;TLPX为发动机推力偏斜角;ZX-Y、ZX-Z为上升器Y、Z方向质心偏心值;ZDGL-Y、ZDGL-Z为上升器Y、Z方向转动惯量;JS-T为热解锁时间间隔;YL-FY、YL-FZ为Y、Z方向羽流力;YL-TY、YL-TZ为Y、Z方向羽流力矩。
3 起飞动力学近似模型
对上升器月面起飞稳定性进行研究,仅采用动力学仿真计算的方法,不仅仿真成本较高,周期过长;而且由于目标函数和变量之间的强非线性关系,以及变量之间的相关性,难以进行准确的人工分析。由于近似模型是用简单的函数关系近似替代实际的复杂仿真模型,因此在起飞稳定性分析和优化设计中采用近似模型可以大幅提高效率。
采用优化拉丁超立方[12]试验设计方法选取样本点构建起飞稳定性影响因子变量与起飞稳定性目标函数间近似函数的显示关系,近似模型中14个影响因子最少只需30组数据样本。
3.1径向基神经网络
探测器起飞稳定性属于高度非线性问题,采用传统的响应面方法构造的全局响应面精度往往不高,而径向基函数神经网络方法可用于全局显式模型的建立[13-15]。因此,可以采用径向基神经网络建立上升器起飞稳定性分析的近似模型。
(1)径向基函数

(1)
式中:λj和βj分别为径向基函数φ(‖X-X(j)‖)和多项式函数fj(X)的待定系数。
(2)径向基神经网络结构模型
径向基神经网络[15]的神经元如图2所示。
节点激活函数采用径向基函数,通常定义为空间任一点到某一中心之间的欧式距离的单调函数,具体函数如下:
(2)

图2 径向基神经元模型Fig.2 RBF neural net model
由图2所示的径向基神经元结构可以看出,径向基神经网络的激活函数是以输入向量和权值向量之间的距离‖dist‖作为自变量的。径向基神经网络的激活函数的一般表达式为:
(3)
3.2近似模型有效性验证
(1)误差分析
利用径向基神经网络对上述优化拉丁超立方试验设计方法的试验数据进行训练,得到近似模型网络结构,从30组训练样本中随机选取5组数据对近似模型进行误差分析,分析结果如表2所示,表中UR2、UR3、VR2、VR3分别为上升器点火2 s后Y、Z方向姿态角和姿态角速度。
由表2可知,随机选取的5组数据中,采用径向基神经网络训练得到的近似模型计算结果与有限元仿真结果最大相对误差为8%,在工程研究允许误差范围内,可以采用此近似模型来代替有限元模型。

表2 近似模型误差分析
(2)方差分析
方差分析认为响应的总方差来源于两部分的贡献,分别为近似模型本身,以及拟合误差[13]。方差分析需要采用离均差平方和,定义如下:
(4)

采用R2来描述前文中的径向基神经网络近似模型的拟合精确度,R2越接近1表明拟合得越精确,R2定义为:R2=SModel/STotal。如图3所示,对于上升器的UR2、UR3、VR2、VR3的R2方差均较接近于1,近似模型较为准确。
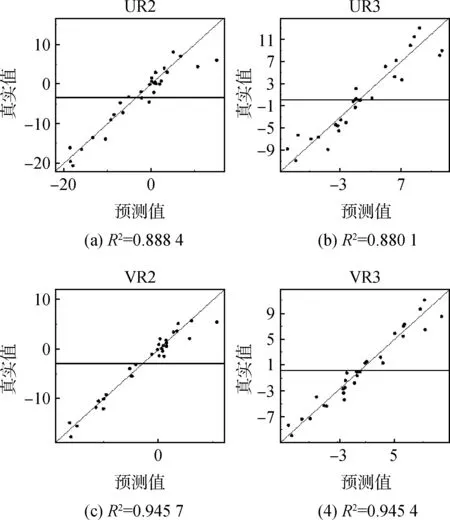
图3 UR2、UR3、VR2、VR3的R2方差分析Fig.3 R2variance analysis of UR2、UR3、VR2 and VR3
4 起飞稳定性影响因素敏感度分析
结合优化拉丁超立方试验设计方法,对上述影响因素进行工况规划并进行有限元计算,在获得训练样本的基础上,采用径向基神经网络获得了其近似模型并用于影响因素敏感度分析。
4.1因素无量纲化
对于上升器起飞稳定性影响因素,由于性质不同,计量单位不同等,缺乏因素综合性。此外,当各影响因素间的数值水平相差很大,如果直接用各因素原始值进行分析,就会突出数值水平较高的因素在综合分析中的作用,相对削弱数值水平较低因素的作用,从而使各因素以不等权的方式参加运算分析。为避免这一点,解决各影响因素数值可综合性的问题,需要对各影响因素数值进行无量纲化处理。采用直线型无量纲化方法[16],其计算的公式为:
(5)
4.2影响因素敏感度分析
采用多元二次回归方法,在径向基神经网络近似模型学习训练的基础上,对上升器起飞稳定性影响因素进行敏感度分析。
多元二次回归模型[17]为:
(6)
以两个输入变量模型为例,其多项式构成如下:

(7)
则其导数为:
dy=b1dx1+b2dx2+2b3x1dx1+
(8)

(1)影响因素线性主效应分析
计算得到上升器起飞过程中,其角位移、角速度对上升器起飞稳定性影响因子的敏感度分别如图4~图7所示,图中坐标左边条形表示负效应,右边条形表示正效应。

图4 UR2对起飞稳定性影响因素的敏感性Fig.4 Sensitivity of influence factors to UR2 of take-off stability
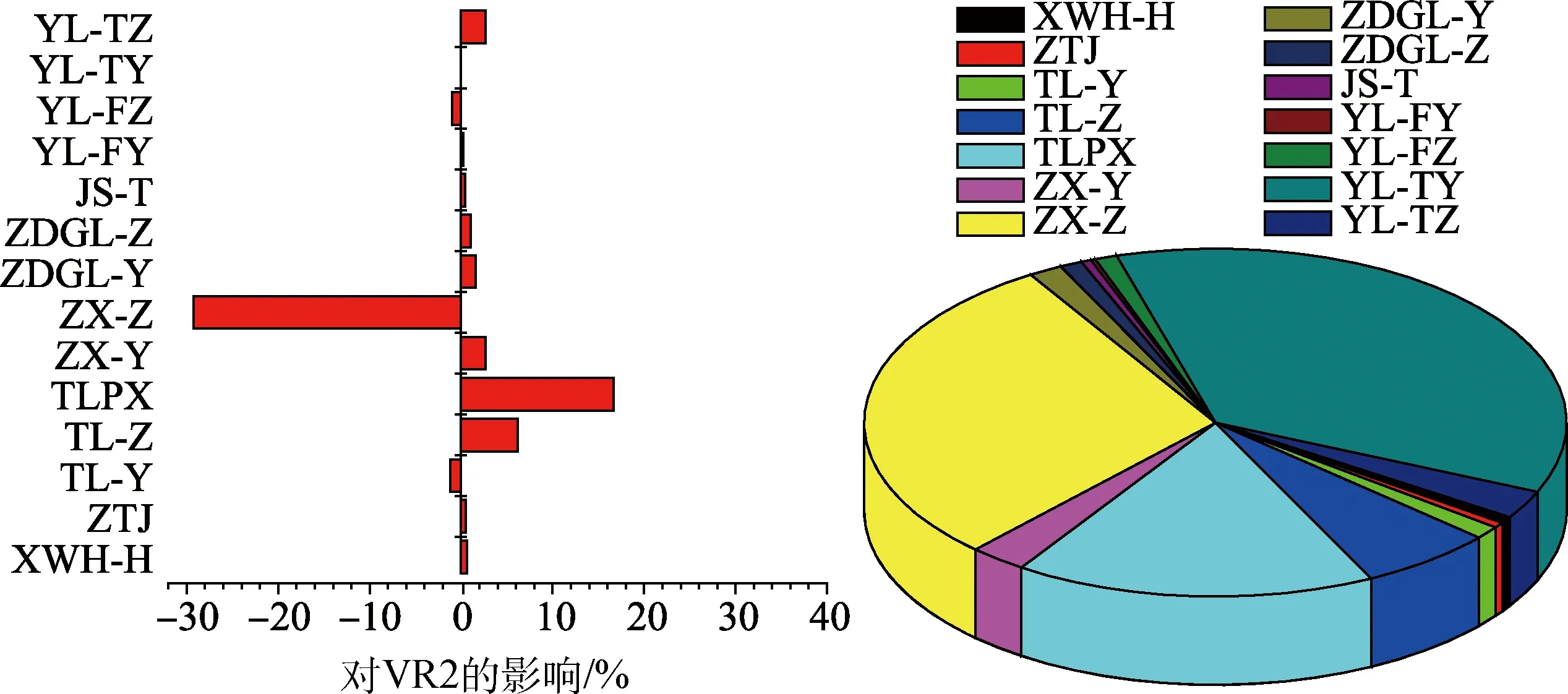
图6 VR2对起飞稳定性影响因素的敏感性Fig.6 Sensitivity of influence factors to VR2 of take-off stability
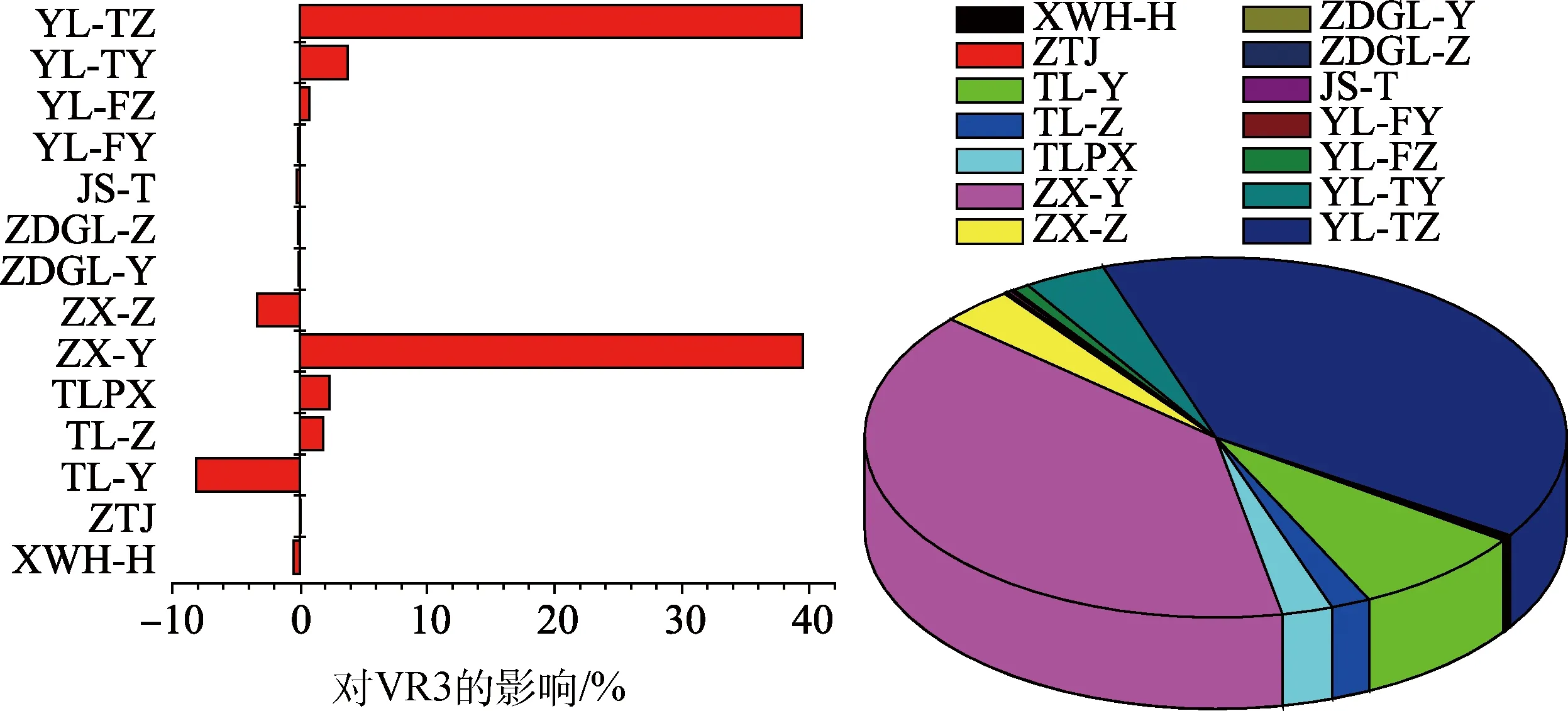
图7 VR3对起飞稳定性影响因素的敏感性Fig.7 Sensitivity of influence factors to VR3 of take-off stability
由图4可以看出上升器Y方向角位移(UR2)对影响因子的敏感性高低顺序为:YL-TY、ZX-Z、TLPX、TL-Z、YL-TZ、ZDGL-Y、ZX-Y、YL-FZ、TL-Y、ZDGL-Z、XWH-H、JS-T、ZTJ、YL-FY。
由图5可以看出上升器Z方向角位移(UR3)对影响因子的敏感性高低顺序为:YL-TZ、ZX-Y、TL-Y、YL-TY、ZX-Z、TL-Z、TLPX、YL-FZ、XWH-H、ZDGL-Y、YL-FY、ZDGL-Z、JS-T、ZTJ。
由图6可以看出上升器Y方向角速度(VR2)对影响因子的敏感性高低顺序为:YL-TY、ZX-Z、TLPX、TL-Z、ZX-Y、YL-TZ、ZDGL-Y、TL-Y、ZDGL-Z、YL-FZ、XWH-H、ZTJ、JS-T、YL-FY。
由图7可以看出上升器Z方向角速度(VR3)对影响因子的敏感性高低顺序为:ZX-Y、YL-TZ、TL-Y、YL-TY、ZX-Z、TLPX、TL-Z、YL-FZ、XWH-H、JS-T、YL-FY、ZDGL-Y、ZDGL-Z、ZTJ。
在稳定性分析时,选用对上升器角位移敏感性最高的影响因素和对角速度敏感性最高的影响因素为分析变量,以判定上升器月面起飞的稳定性。
(2)影响因素二阶效应分析
由式(8)可知,分析影响因素的敏感度还需要分析影响因素的二阶效应,且上升器起飞稳定性影响因子之间可能交互作用,如推力偏心和质量偏心对起飞稳定性的影响是两者共同作用的结果。二阶效应包括二阶主效应和交互效应,取前10组敏感度较大的结果,如图8~图11所示,图中坐标左边条形表示负效应,右边条形表示正效应。
由图8~图11可以看出,上升器角位移、角速度对ZX-Y、ZX-Z、YL-FY、YL-FZ、ZTJ和TLPX等因素交互效应的二阶敏感性也较大。

图8 UR2对起飞稳定性影响因素的二阶敏感性Fig.8 Two order sensitivity of influence factors to UR2 of take-off stability
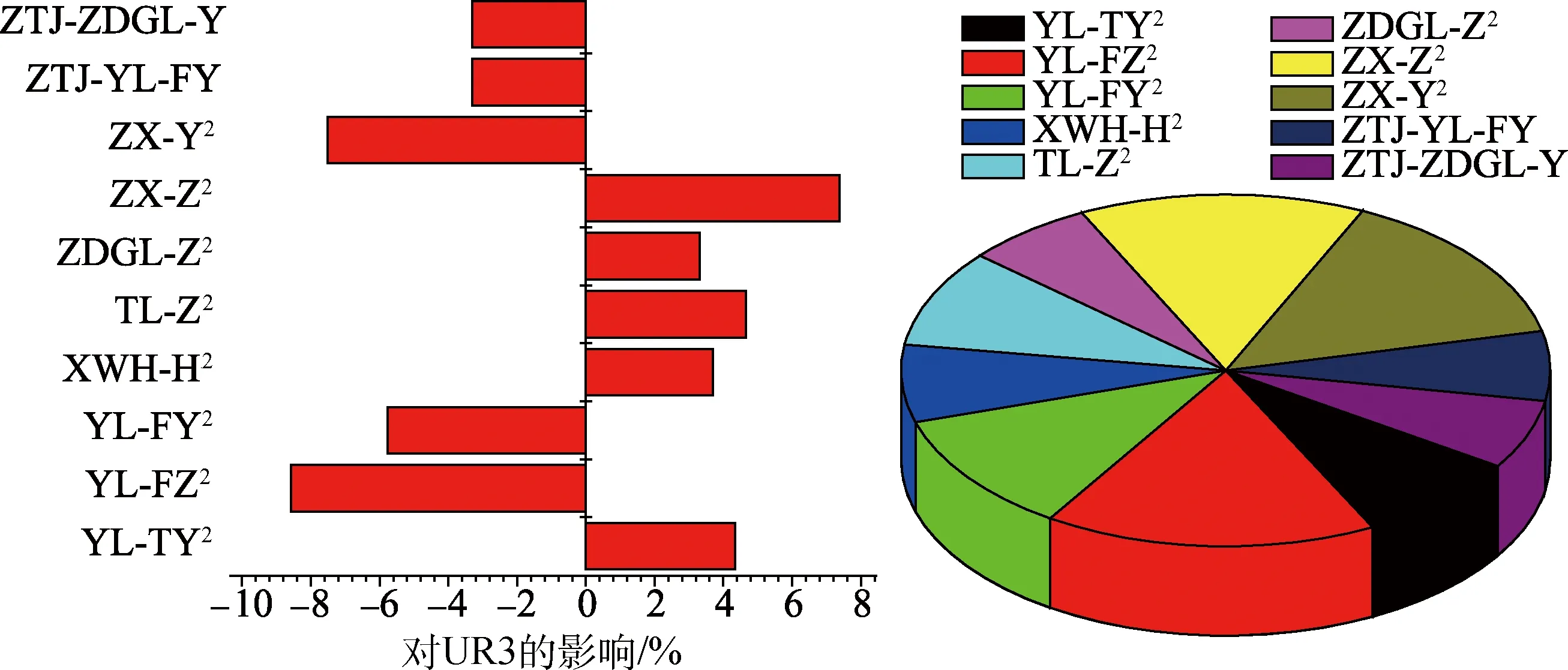
图9 UR3对起飞稳定性影响因素的二阶敏感性Fig.9 Two order sensitivity of influence factors to UR3 of take-off stability
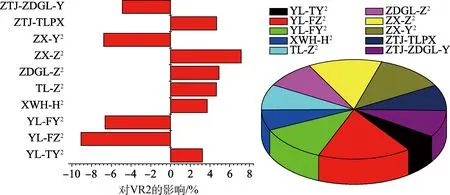
图10 VR2对起飞稳定性影响因素的二阶敏感性Fig.10 Two order sensitivity of influence factors to VR2 of take-off stability
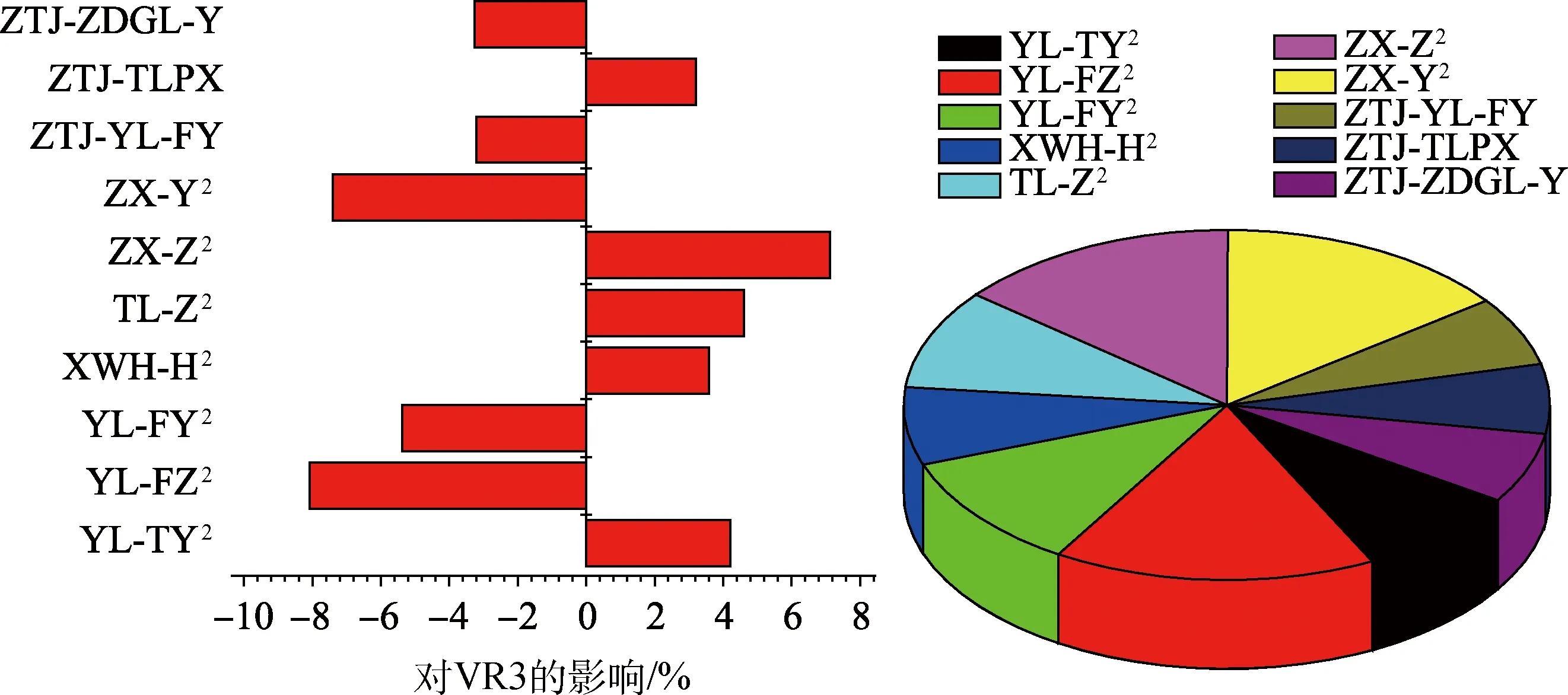
图11 VR3对起飞稳定性影响因素的二阶敏感性Fig.11 Two order sensitivity of influence factors to VR3 of take-off stability
5 上升器起飞稳定性分析
为了使姿控发动机安全准确地对上升器进行姿态控制,在上升器主发动机点火后2 s时刻,即姿控发动机开始工作时,需满足上升器的姿态角和姿态角速度绝对值分别不超过5°和5(°)/s。
5.1单因素边界分析
基于上述近似模型,以上升器的姿态角和姿态角速度绝对值为边界条件,分别对上升器的单个影响因素进行边界分析,其他因素均取相应的基准值,具体分析结果如表3所示。
由表3可知,上升器起飞稳定性影响因素中,敏感度较大的影响因素,其边界条件比预设的取值范围小,因此在设计时需要注意这些参数的保证,以免影响上升器的起飞稳定性。
5.2多因素临界条件分析
仅仅基于其他因素取基准值对单个因素的边界条件分析是远远不够的,由于工程设计以及着陆过程的不确定性等原因,需要在其他影响因素取某一值的情况下,对某因素进行边界条件分析。建立起飞稳定性多因素综合判据中最困难的是对多因素的表达,本文将采用空间的方式把单因素作为维度,通过曲面的方式来展示起飞稳定性的多因素临界条件。

表3 单影响因素取值边界
影响上升器起飞稳定性的因素很多,不过可以根据因素的敏感性抽取关键因素,用函数表达建立综合判据方程,假设起飞稳定性临界条件由3个关键因素变量所确定,其空间就是三维的。如果表征稳定状态的参量在三维空间的区域以内,表明上升器处于稳定状态,在空间以外表明上升器将处于非稳定状态。表征这个三维空间表面的函数方程则为上升器起飞稳定性临界条件的表达式,采用通用表达式:

(9)
编写上升器起飞稳定性临界条件分析软件,在训练好的径向基神经网络近似模型的基础上,采用蒙特卡洛方法对其他因子不同取值的某个因素进行边界条件分析,以确定其取值上下界限,优化上升器起飞稳定性设计参数,为探测器设计提供一定的参考。由上述分析可知,上升器起飞稳定性影响因子敏感度超过10%的就5个,即ZX-Y、ZX-Z、YL-TY、YL-TZ、TLPX,因此设计5个相应的组合参数。
上升器起飞稳定性影响因子很多,根据式(9)选择3个主要的组合参数,结合上升器起飞稳定性组合边界条件分析软件,以确定上升器起飞稳定性多因素临界条件。以ZX-Y、YL-TY、TLPX作为3个变量为例,确定起飞稳定性多因素临界条件,如图12所示,图中两个曲面分别为YL-TY随ZX-Y和TLPX变化的上下边界,因此,下曲面以上以及上曲面以下的3个参数取值均可保证上升器起飞稳定,边界以外的其他所有取值组合上升器起飞均不稳定。
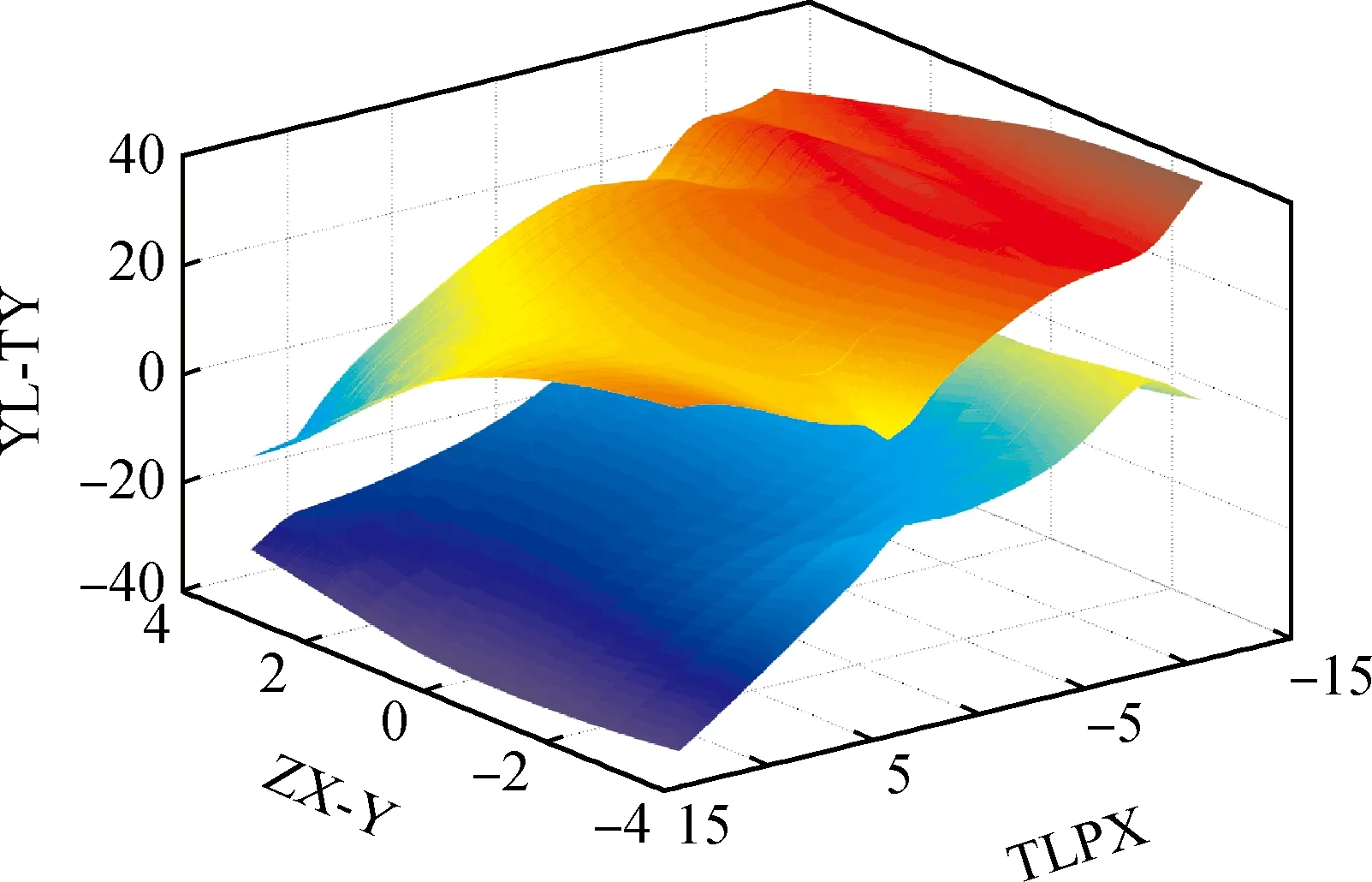
图12 起飞稳定性综合判据Fig.12 Comprehensive criteria of take-off stability
6 结束语
本文结合优化试验设计方法和径向基神经网络建立了上升器起飞过程动力学近似模型,并以此定量地分析了影响因素的敏感度,获得了上升器起飞稳定性临界条件和综合判据,得到如下结论:
1)采用径向基神经网络建立的上升器起飞过程动力学近似模型精度较高,可以代替有限元模型。
2)上升器起飞稳定性影响因素敏感度较大的为质心位置、推力偏斜和羽流力矩,且影响因素还具有较强的二阶效应。
3)采用空间的方式把单因素作为维度,通过曲面的边界可以直观地建立起飞稳定性的多因素临界条件。
References)
[1]WALTON W C, HERE R W, LEONARD H W. Studies of touchdown stability for lunar landing vehicles[J]. Journal of Spacecraft, 1964,1(5):552-556.
[2]STUBBS S M. Experimental investigation of the landing dynamics of three-legged spacecraft models[R]. NASA TN D-7664, Langley Research Center, 1974.
[3]CHEN J B, HONG N. Overloading of landing based on the deformation of the lunar lander[J]. Chinese Journal of Aeronautics, 2008(21):43-47.
[4]朱汪, 杨建中. 月球着陆器软着陆机构着陆稳定性仿真分析[J]. 宇航学报, 2009, 30(5):1792-1796.
ZHU W, YANG J Z. Touchdown stability simulation of landing gear system for lunar lander[J]. Journal of Aeronautics, 2009, 30(5):1792-1796(in Chinese).
[5]胡亚冰, 孙毅. 腿式月球着陆器静态稳定性研究[J]. 中国空间科学技术, 2009,29(2):17-24.
HU Y B, SUN Y. Research on static stability of lunar lander with legs[J]. Chinese Space Science and Technology, 2009,29(2):17-24(in Chinese).
[6]李罗刚, 崔祜涛, 马春飞, 等. 月面返回最优轨道设计[J]. 哈尔滨工业大学学报, 2010,42(11):1707-1710.
LI L G, CUI K T, MA C F, et al. Optimal orbit design of returning from moon[J]. Journal of Harbin Institute of Technology, 2010, 42(11):1707-1710(in Chinese).
[7]SOSTARIC R R, MERRIAM R S. Lunar ascent and rendezvous trajectory design[C]∥Proc. of the 31st Annual AAS Rocky Mountain Guidance and Control Conference, 2008:1-23.
[8]ROSE M B, GELLER D K. Linear covariance techniques for powered ascent[C]∥Proc. of the AIAA Guidance, Navigation, and Control Conference, 2010:1-21.
[9]李鑫, 刘莹莹, 周军. 载人登月舱上升入轨段的制导律设计[J]. 系统工程与电子技术, 2011, 33(11):2480-2484.
LI X, LIU Y Y, ZHOU J. Design of guidance law for lunar ascent phase of manned lunar module[J]. Systems Engineering and Electronics, 2011, 33(11):2480-2484(in Chinese).
[10]胡建国, 马大为, 乐贵高, 等. 月壤撞击坑对探测器着陆性能影响研究[J]. 兵工学报. 2013, 34(8): 1046-1050.
HU J G, MA D W, LE G G, et al. Study on influence of impacted craters on landing performance of lunar lander[J]. Acta Armamentarii, 2013, 34(8):1046-1050(in Chinese).
[11]胡建国, 马大为, 朱忠领, 等. 蜂窝材料率相关本构模型及其在月球探测器中的应用研究[J]. 振动与冲击, 2014, 33(7): 114-119.
HU J G, MA D W, ZHU Z L, et al. A rate-dependent constitutive model for honeycomb material and its application in a lunar lander[J]. Journal of Vibration and Shock, 2014, 33(7): 114-119(in Chinese).
[12]陈魁. 试验设计与分析[M]. 北京: 清华大学出版社, 2005: 5-28.
[13]穆雪峰, 姚卫星, 余雄庆, 等. 多学科设计优化中常用代理模型的研究[J]. 计算力学学报, 2005, 22(5):608-612.
MU X F, YAO W X, YU X Q, et al. A survey of surrogate models used in MDO[J]. Chinese Journal of Computational Mechanics, 2005, 22(5):608-612 (in Chinese).
[14]WU Z M. Generalized bochners theorem for radial function[J]. Approximation Theory and it′s Application, 1997, 12:47-57.
[15]史忠植. 神经网络[M]. 北京: 高等教育出版社, 2009.
[16]谈庆明. 量纲分析[M]. 合肥: 中国科学技术大学出版社, 2005.
[17]赖宇阳. Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012.
(编辑:高珍)
Study on take-off stability boundaries of lunar detector
HU Jianguo*,SHI Yaozu,ZHAO Yi,XU Hongbin
Xi′an Modern Control Technology Research Institute, Xi′an 710065, China
The take-off stability of lunar detector is an important performance index of an ascender′s taking off from the moon′s surface.By choosing some main influence factors of take-off stability, the take-off dynamic approximation model of ascender was established combining with an optimal latin hypercube experimental design method and the RBF neural network, and the sensitivity of the factors for the angular displacement and velocity was quantitatively analyzed. Based on the stability criterion that the angular displacement and angular velocity of ascenders was 5° and 5(°)/s respectively, the boundary values of a single influence factor were given.A program for multiple factors boundary analysis of the ascender take-off stability was compiled.The boundary expression of the ascender take-off stability is founded by the way of three-dimensional space, and the take-off stability boundaries were determined with a sample.
spacecraft structure and design; lunar detector; take-off stability; approximation model; sensitivity; critical condition; compositive criterion
10.16708/j.cnki.1000-758X.2016.0056
2016-06-03;
2016-07-27;录用日期:2016-08-22;
时间:2016-09-2113:41:20
http:∥www.cnki.net/kcms/detail/11.1859.V.20160921.1341.004.html
胡建国(1986-), 男, 博士, 高工, super-jianguo@163.com,研究方向为发射技术
HUJG,SHIYZ,ZHAOY,etal.Studyontake-offstabilityboundariesoflunardetector[J].ChineseSpaceScienceandTechnology, 2016,36(5):40-47(inChinese).
V423.6
A
http:∥zgkj.cast.cn
引用格式:胡建国,史耀祖,赵毅,等.探测器月面起飞稳定性边界条件研究[J].中国空间科学技术, 2016,36(5):40-47.

