基于状态转移矩阵的航天器多脉冲悬停方法
程博,袁建平,马卫华
1.西北工业大学 航天学院,西安 7100722.北京宇航系统工程研究所,北京 100076 3.航天飞行动力学技术重点实验室,西安 710072
基于状态转移矩阵的航天器多脉冲悬停方法
程博1,2,3,袁建平1,3,*,马卫华1,3
1.西北工业大学 航天学院,西安 7100722.北京宇航系统工程研究所,北京 100076 3.航天飞行动力学技术重点实验室,西安 710072
基于航天器相对运动的状态转移矩阵描述,研究了空间相对悬停的多脉冲控制方法,解决了工程实践中连续推力悬停轨道控制技术对航天器控制推进系统要求较高的难题。给出了两航天器在圆、椭圆和双曲线等圆锥曲线参考轨道上相对运动的状态转移矩阵描述。在此基础上,定性分析了椭圆参考轨道偏心率对悬停精度的影响,推导了航天器多脉冲悬停速度脉冲控制量的计算方法。数值仿真算例显示,该方法可有效实现一定悬停精度要求下的空间相对悬停控制,且随着一个轨道周期内脉冲数的增加,相对悬停的效果得到提升。
航天器;相对运动;状态转移矩阵;多脉冲;悬停
随着航天器在轨服务技术、深空探测技术等研究的深入推进和相关工程实践的广泛开展,作为其重要支撑技术的航天器悬停技术成为近年来逐渐兴起的研究方向[1]。
航天器悬停是指通过力和力矩控制,使主动航天器相对目标航天器的位置始终保持不变,在目标航天器的质心轨道坐标系中,主动航天器相对目标航天器仿佛是静止悬停于某个固定点上。主动航天器在力的作用下相对于目标航天器在一段时间内相对位置保持不变的轨道称为悬停轨道[2]。目前国内外开展的航天器悬停技术应用研究主要有任务航天器相对小天体的悬停技术研究和任务航天器相对目标航天器的悬停技术研究[3-8]。
文献[3]基于两体引力模型,研究了航天器相对小行星在体固连坐标系和惯性坐标系下的悬停控制方法,并进行了悬停控制稳定性分析。文献[4]假设太阳帆反射面积可变,给出了太阳帆在哑铃形小行星引力场内悬停的动力学方程,并对可行悬停探测区域进行了分析。文献[5]研究了R-bar和V-bar方向上主动航天器的悬停加速度,给出了悬停控制加速度的解析表达形式,并分析了参考轨道平面内外的悬停速度增量情况。文献[6]推导的相对悬停控制力的解析表达式考虑了地球引力摄动的J2项影响,并对产生最大和最小控制力及燃料消耗的悬停点进行了分析。上述悬停应用研究的相对运动模型均基于连续推力条件,要求任务航天器的推进系统能够提供大小和方向均连续可变的控制加速度。
在目前的工程实践中,实现对航天器轨道控制推力的连续精确调节仍非常困难,因此有学者提出基于分段脉冲推力的思想,使主动航天器实现相对目标悬停的目的[2,7-8]。该方法基于线性化后的相对运动动力学解析解,计算出实现分段悬停所需要的速度脉冲大小、方向以及施加速度脉冲的时间点。文献[7]基于C-W方程的解析解,对水滴形悬停轨道的冲量控制策略和进入方法进行了研究。文献[8]等基于相对轨道要素的相对运动描述,给出了脉冲推力作用下的水滴悬停构型的形成机理和相关参数的影响分析。上述研究有效降低了空间相对悬停的工程实施难度,但其相对运动模型均是建立在圆或近圆参考轨道条件下,限制了悬停控制方法的应用范围。
本文基于航天器相对运动的状态转移矩阵描述方法给出了航天器空间悬停的多脉冲方法,实现了脉冲推力作用下的空间悬停控制。本文给出的悬停控制方法利于工程实现,可采用具备多次启停功能的大推力轨控发动机实现轨道机动的冲量控制[9-10]。同时,本文方法适用于圆、椭圆和双曲线等圆锥曲线参考轨道的空间悬停任务。
1 相对悬停的轨道动力学

图1 航天器悬停坐标系Fig.1 Coordinate system for hovering spacecraft
为了对航天器悬停的轨道动力学进行分析,首先建立主动航天器与目标航天器之间的相对运动关系,涉及的坐标系主要有J2000地心赤道惯性坐标系O-XYZ(简称“惯性坐标系”)和目标航天器质心轨道坐标系o-xyz(简称“轨道坐标系”)。如图1所示,惯性坐标系的原点在地心O上,X轴在赤道面内指向春分点,Y轴在赤道面内与X轴垂直指向东,Z轴与X轴、Y轴构成右手正交坐标系。轨道坐标系的原点在目标航天器质心o上,x轴沿地心指向目标航天器方向,y轴在轨道平面上与x轴垂直,指向航天器的速度方向,z轴和x轴、y轴构成右手正交坐标系。
如图1所示,在目标航天器轨道坐标系下,主动航天器相对目标航天器运动的动力学方程为[11-12]:
(1)

对于航天器的悬停任务,由于相对静止的特点,主动航天器在目标航天器轨道坐标系中的相对速度以及相对加速度均等于零[2],即

(2)
将式(2)带入式(1)得:
(3)
式(3)为航天器悬停时应满足的动力学方程,通过它可计算出实现悬停需施加在主动航天器上的控制加速度。由式(3)可以看出该控制加速度为时变的连续量。
2 相对运动状态转移矩阵
两航天器相对悬停时,相对距离ρ及其分量与目标航天器轨道半径相比为小量,故它们的模之比ρ/Rt、x/Rt、y/Rt和z/Rt的二阶及二阶以上项为高阶小量,在进行近似计算时,可以略去。对式(1)进行简化,略去二阶以上小量后可得简化的相对运动方程[12]:
(4)
分析方程(4)可知,求解该二阶非齐次微分方程组较为复杂,且当主动航天器所受外力a为任意时间函数时,不存在一般解析解[12-13]。为得到两航天器相对运动的解析表达形式,需要对相对运动方程(4)进行简化和求解。
假设主动航天器不受外力作用,以自由状态与目标航天器相对运动,可将方程(4)化成齐次形式,即
对于目标航天器,其角动量h的模为
(5)
目标航天器以开普勒轨道运行,其角动量守恒,应为常值,故由式(5)可得:
(6)
式中:k=μh-3/2,为常值参量。
应用变量代换法,将方程(4)中对时间的导数转换成对目标航天器真近角θ的导数得:
(7)
若令ξ=1+ecosθ,则有下面等式成立:
(8)
将式(8)带入式(7)得:

(9)
对式(9)进行变量代换:
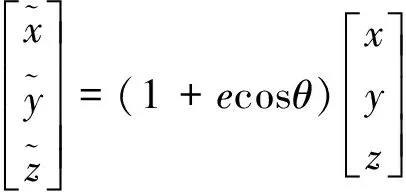
(10)
则相对运动方程可写成如下简单形式:

(11)
对式(11)进行求解可得相对运动状态的表达式[14]:
(12)

式中:J=(h/p2)(t-t0);c=ξcosθ;s=ξsinθ;c′=-sinθ-esin(2θ);s′=cosθ+ecos(2θ)。
由式(12)可得:
(13)

(14)
将式(14)代入Φθ表达式,并求Φθ0行列
式有:
(15)
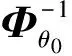
(16)
值得注意的是,对于常见的椭圆参考轨道相对运动,其目标航天器轨道即参考轨道的几何描述为:
(17)
分析式(17)可知,在目标航天器轨道半长轴at不变的情况下,若增大其偏心率,则目标航天器轨道半径Rt将减小。因本文在进行相对运动动力学方程求解时进行了一阶近似,舍去了ρ/Rt的二阶及二阶以上的小量。故在悬停距离ρ不变的情况下,增大参考轨道偏心率,将增加式(13)所描述的两航天器相对运动的方法误差。因此在实际工程应用中,应结合相对运动精度要求来确定状态转移矩阵的应用范围。
3 基于状态转移矩阵的多脉冲悬停
基于第1节的推导可以得出连续推力作用下的空间相对悬停控制,但在实际的航天任务中,往往很难实现对主动航天器轨道控制推力大小和方向的连续自由控制,则两航天器相对加速度始终为零的情况很难长时间保持。从空间悬停的基本目标出发,即实现两航天器相对位置保持不变,舍去对相对加速度的控制,考虑采用冲量控制手段,在一个固定周期内使两航天器相对运动始末的相对位置不变,相对速度为零。若该固定周期足够短或满足工程应用,则可近似认为实现两航天器在空间的“持续”相对悬停,即两航天器的多脉冲相对悬停。

(18)
式(18)的每个子阵均为三维方阵。则式(13)可写成如下形式:
(19)
(20)
对于悬停的两航天器,主动航天器相对目标航天器运动终止时刻的相对距离应与初始时刻相同。则由式(19)可得:
(21)
(22)

(23)
需要注意的是,这里的相对运动状态均是基于式(10)变量代换之后的,实际计算时应将其转回到目标航天器质心轨道坐标系下。
4 仿真分析
为了直观展示本文给出的航天器多脉冲悬停方法的效果,本节给出了相关数值仿真结果。仿真中,目标航天器在椭圆开普勒轨道上飞行,其轨道参数如表1所示。

表1 目标航天器初始条件
4.1航天器多脉冲悬停
设初始时刻主动航天器相对目标航天器的位置ρ0(单位km)和速度v0(单位km/s)在目标航天器轨道坐标系下的分量分别为:
要求的理论悬停点d与两航天器初始时刻的相对位置ρ0相同。分别选择在一个轨道周期内进行5次、10次和20次脉冲悬停,且每次脉冲变轨时间相同。图2给出了主动航天器相对目标航天器多脉冲悬停的相对运动轨迹的仿真结果。
从图2可以看出,悬停脉冲数越多,相对运动轨迹越平滑,即越趋向于在悬停点的稳定悬停。同时,相对运动轨迹与悬停点之间有一定偏差,该偏差的产生是由于,本文给出的多脉冲悬停方法在计算相对运动初始时刻的速度脉冲时是以脉冲变轨初始时刻和结束时刻的相对位置相同为前提的,且基于状态转移矩阵的相对运动描述是在舍去了二阶项的基础上得出,与非线性表达方法相比存在方法误差,多次脉冲变轨产生了误差累积,于是表现出相对运动轨迹与设定的悬停点之间存在一定的偏差。但从仿真结果来看,偏差相对较小,总体可控。

图2 多脉冲悬停相对运动轨迹Fig.2 Trajectory of the relative motion of multiple-pulse hovering
4.2参考轨道偏心率对悬停的影响
设多脉冲悬停的悬停点平均误差为:
(24)
式中:N为悬停脉冲数;Δri为各悬停点的悬停误差矢量。图3给出了参考轨道偏心率e与Δr之间的变化规律。

图3 参考轨道偏心率对悬停的影响Fig.3 Influence of eccentricity of reference orbit
从图3可以看出,随着目标航天器轨道偏心率e增大,Δr不断增大,且增加的速度不断加快。本文第2节给出的相对运动描述方法本身适用于任意偏心率椭圆参考轨道,但随着参考轨道偏心率的增大,本文给出的多脉冲变轨方法的累积误差及悬停点误差积累的速度不断增加,导致在较大偏心率参考轨道情况下,多脉冲悬停的精度有所下降。工程应用时可根据对悬停精度的要求进行综合考虑。
5 结束语
基于航天器相对运动的状态转移矩阵描述方法,本文给出了航天器空间悬停的多脉冲方法,解决了基于连续推力作用的空间悬停轨道控制技术在工程实践中对航天器控制推进系统要求较高的难题,实现了脉冲推力作用下的空间悬停控制。本文给出的空间悬停控制方法适用于圆、椭圆和双曲线等圆锥曲线参考轨道的空间悬停任务,应用范围广。参考轨道偏心率会对悬停效果产生一定影响。本文建立了基于相对运动状态转移矩阵的悬停脉冲控制量线性计算方法,计算简便,利于工程实现和在轨应用。
对文中给出的航天器多脉冲悬停方法进行数值仿真分析,结果显示,在一定精度范围内,本文方法可实现主动航天器相对目标航天器的空间相对悬停,且随着一个轨道周期内脉冲数的增加,悬停效果得到提升。
本文给出的航天器多脉冲悬停方法推导过程中进行了一阶近似,且未考虑地球引力摄动的影响,相对悬停存在一定误差,且该误差存在累积效应,会对悬停精度产生影响,后续应进一步研究消除相对悬停误差的有效方法,以提升悬停精度,但对于悬停精度要求不高的工程任务,本文给出的方法具有应用价值。
References)
[1]朱亚文. 航天器悬停特性分析与控制方法研究[D]. 长沙:国防科学技术大学,2010.
ZHU Y W. Study on orbital characteristics and control of hovering spacecraft[D]. Changsha: National University of Defense Technology, 2010(in Chinese).
[2]袁建平,李俊峰,和兴锁,等. 航天器相对运动轨道动力学[M]. 北京:中国宇航出版社,2013:482-561.
[3]BROSCHART S B, SCHEERES D J. Control of hovering spacecraft near small bodies: application to asteroid 25143 Itokawa[J]. Journal of Guidance, Control, and Dynamics, 2005,28(2):343-354.
[4]曾祥远,龚胜平,李俊峰,等. 应用太阳帆悬停探测哑铃形小行星[J]. 深空探测学报,2015,2(1):48-52.
ZENG X Y, GONG S P, LI J F, et al. Hovering flight over elongated asteroids by using solar sails[J]. Journal of Deep Space Exploration, 2015,2(1):48-52(in Chinese).
[5]ZHANG J R, ZHAO S G, YANG Y Z. Characteristic analysis for elliptical orbit hovering based on relative dynamics[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013,49(4):2742-2750.
[6]DANG Z H, WANG Z K, ZHANG Y L. Modeling and analysis of relative hovering control for spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2014,37(4):1091-1102.
[7]潘屹. 航天器相对运动水滴型悬停轨道研究[J]. 航天器工程,2014,23(4):13-18.
PAN Y. Study on spacecraft relative drip-drop hovering orbit[J]. Spacecraft Engineering, 2014,23(4):13-18(in Chinese).
[8]饶殷睿,韩潮,殷建丰,等. 航天器悬停构型设计与控制方法[J]. 航空学报,2015,36(7):2361-2371.
RAO Y R, HAN C, YIN J F, et al. Method of spacecraft hovering formation design and control[J].Acta Aeronautica et Astronautica Sinica, 2015,36(7):2361-2371(in Chinese).
[9]杭观荣,洪鑫,康小录. 国外空间推进技术现状和发展趋势[J]. 火箭推进,2013,39(5):7-15.
HANG G R, HONG X, KANG X L. Current status and development trend of space propulsion technologies abroad[J]. Journal of Rocket Propulsion, 2013,39(5):7-15(in Chinese).
[10]姜文龙,杨成虎,林庆国. 高性能卫星用490N轨控发动机研究进展[J]. 火箭推进,2011,37(6):9-13.
JIANG W L, YANG H C, LIN G Q. Development of high performance 490N apogee engine for satellites[J]. Journal of Rocket Propulsion, 2011,37(6):9-13(in Chinese).
[11]郗晓宁. 近地航天器轨道基础[M]. 长沙:国防科技大学出版社,2003:244-269.
[12]刘暾, 赵均. 空间飞行器动力学[M]. 哈尔滨:哈尔滨工业大学出版社,2003:83-101.
[13]张宗达,刘锐,王勇,等. 工科数学分析[M]. 北京:高等教育出版社,2001:221-266.
[14]YAMANAKA K, ANKERSEN F. New state transition matrix for relative motion on an arbitrary elliptical Orbit[J]. Journal of Guidance, Control and Dynamics, 2002,25(1):60-66.
[15]张爱萍. 可逆矩阵的判定及求法[J]. 赤峰学院学报,2011,27(3):12-13.
[16]郑宝东,邓廷权. 线性代数与空间解析几何[M]. 北京:高等教育出版社,2001:1-56.
(编辑:高珍)
Spacecraft multiple-pulse hovering method based on state transition matrix
CHENG Bo1,2,3,YUAN Jianping1,3,*,MA Weihua1,3
1. School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China 2. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China 3. National Key Laboratory of Aerospace Flight Dynamics, Xi′an 710072, China
Based on a state transition matrix, a method for spacecraft multiple-pulse hovering was presented. The relative motion dynamics model and the state transition matrix were introduced to describe the relative motion of two spacecraft in circular, elliptical and hyperbolic reference orbits. A method of achieving the orbit-transfer velocity increment for hovering was deduced using the state transition matrix. The numerical simulation shows that the proposed method can achieve spacecraft relative hovering effectively. With the increasing of impulse number, the precision of relative hovering is promoted. Moreover, the precision of relative hovering is influenced by the eccentricity of reference orbit.
spacecraft;relative motion;state transition matrix;multiple-pulse;hovering
10.16708/j.cnki.1000-758X.2016.0061
2016-03-11;
2016-06-19;录用日期:2016-08-22;
时间:2016-09-2113:41:17
http:∥www.cnki.net/kcms/detail/11.1859.V.20160921.1341.001.html
程博(1983-),男,博士研究生,cheng_bob@163.com,研究方向为飞行器动力学
袁建平(1957-),男,教授,jyuan@nwpu.edu.cn,研究方向为飞行器设计、航天飞行动力学与控制
V412.4
A
http:∥zgkj.cast.cn
引用格式:程博, 袁建平, 马卫华. 基于状态转移矩阵的航天器多脉冲悬停方法[J]. 中国空间科学技术, 2016,36(5):81-87.
CHENGB,YUANJP,MAWH.Spacecraftmultiple-pulsehoveringmethodbasedonstatetransitionmatrix[J].ChineseSpaceScienceandTechnology, 2016,36(5):81-87(inChinese).

