某纯电动客车横置动力总成悬置设计与刚度优化

胡小生，黄详，董泽伟

（上海科曼车辆部件系统股份有限公司，上海201815）

某纯电动客车横置动力总成悬置设计与刚度优化

胡小生，黄详，董泽伟

（上海科曼车辆部件系统股份有限公司，上海201815）

确定某纯电动客车横置动力总成的三点式悬置安装点，计算符合解耦要求的橡胶软垫刚度组合。

根据扭矩轴原理及布置限制确定悬置安装点；在ADAMS/View中建立悬置系统动力学模型，揭示其固有频率和解耦率分布规律；采用试验设计方法优化悬置的轴向刚度，提升系统解耦率。结果表明，该系统达到了

设计目标要求。

纯电动客车；横置动力总成；悬置系统；试验设计；刚度优化

汽车动力总成悬置设计和解耦的好坏对整车平顺性、动力总成的可靠性都有重要影响［1-6］。不同于动力总成纵置的悬置系统，动力总成横置的悬置系统缺乏严格意义上的对称轴［2］，而且纯电动客车动力总成与传统的动力总成有所不同［3］，从而导致其悬置设计存在差异。因此，关于纯电动客车动力总成悬置设计的研究和工程应用亟需开展。本文依托公司自主开发的复合式电驱动后桥纯电动客车项目，根据扭矩轴原理［2-4］和空间布置限制确定其横置动力总成的悬置点安装方位；借助ADAMS软件和能量解耦率理论［5］对其悬置系统进行解耦分析，并采用DOE的方法对其悬置刚度进行优化设计，以进一步提升解耦率并获得合理的固有频率分布。

1　计算与分析

1.1设计目标

如表1所示，以固有频率和解耦率为设计目标，设定系统的固有频率在5 Hz～17Hz范围内，解耦率在70%～90%之间［6］。根据频域范围和所关注方向频率选取固有频率。动力总成所受激励源主要包括路面激励和电机激振。路面激励经由悬架传递到车架的频率一般低于2.5Hz［6］，但为了防止坏路造成的路面激励频率增加以及缩短固有频率的频域宽度，将固有频率下限取为5 Hz。与发动机有所不同，纯电动客车怠速（暂停）时电机转速为0，考虑到电机响应较快，起步加速时间短，最低转速按常行驶车速20 km/h计算，此时电机转速大概为1 500 r/min，其激振频率为25Hz。系统固有频率应尽量避开此时较低转速时的激振频率。根据隔振原理［7］，激振频率与固有频率之比应满足≥1.414，故固有频率范围上限为17Hz。Z向和Ryy向频率为重点关注对象，两者间隔应大于2Hz；垂向频率要求避开车桥和车身的固有频率12Hz～14Hz，并应尽量避开4Hz～8Hz的人体垂向敏感频率。为防止相邻方向耦合，应尽量保持相邻频率间隔大于1Hz。对于解耦率而言，6个自由度完全解耦不易实现，考虑到动力总成主要承受扭转方向的激振力，故俯仰Ryy方向解耦率应尽可能高，垂向Z的次之，其它方向也应达到70%以上［8］。

1.2建立模型

三点式悬置相比四点式具有成本低、质量轻、装配性好和隔振性优等特点，广泛应用在质量不大的动力总成上［8］。结合本项目情况，考虑到此动力总成质量较轻仅223 kg，因此选用三点式悬置。

如图1所示，此次所选动力总成主要由三相同步电机1和集成式差减速器2两部分组成，坐标系Z向与重力方向相反，X向为半轴轴向，Y向按右手定则选取。其质量参数和惯性参数依据厂家提供数据，在ADAMS中计算合成主惯性积和主轴方位角。由扭矩轴公式［9］解得扭矩轴方位角，在CATIA中作出扭矩轴线3，结合后桥布置空间限制，将左右悬置水平布置在扭矩轴上；考虑到差减速器输出端受扭矩较大，将前悬置水平布置在差减速器末端的半轴附近。

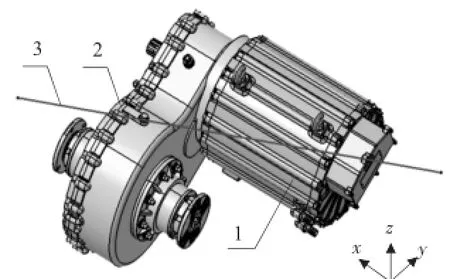
图1　动力总成三维模型

悬置阻尼的作用是降低系统的共振峰值，对其固有特性影响较小，故忽略阻尼，将悬置简化为仅有3个轴向刚度的弹簧［10］。按静载工况确定悬置初始Z向刚度，根据力学关系，左右悬置点连线通过质心；故在静载时，三点式悬置中前悬置几乎不参与承载；左右悬置承受动力总成的重量，其初始垂向刚度按≤5mm的预载压缩量选取。但考虑到悬置系统的扭转刚度，前悬置Z向刚度预设了较大的值。按照固有频率公式估算X、Y向刚度。由于3个悬置点处于空间方位，造成了悬置轴向刚度的差异。在整车坐标系下初始悬置刚度设计如表2所示。

表2　初始刚度值N/mm

如图2所示，为了便于描述将坐标系转化为标准整车坐标系。在ADAMS/View中建立动力总成悬置系统六自由度刚体动力学模型。将动力总成简化为刚体，车身简化为地面，悬置简化为衬套，动力总成通过衬套与地面相连；并将三维数模的质量参数赋予总成部件［11］。

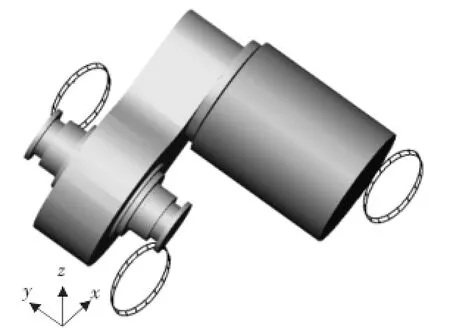
图2　悬置系统动力学模型

1.3解耦分析

对1.2中的动力学模型，在ADAMS/View的Vibration插件中求解出解耦率和固有频率。如表3所示，X、Y、Z、Rxx、Ryy、Rzz分别代表整车坐标系下的纵向、横向、垂向、侧倾、俯仰、横摆自由度。结合1.1节中设计目标可以看出，固有频率均在设计目标范围内；但第3阶Z向和第6阶Ryy向固有频率分别为6.31Hz和14.25Hz，均不在设计目标范围内；另外，1至3阶频率间隔均小于1 Hz，故固有频率分布不合理。除Z向和Ryy向外其余方向解耦率均达到80%以上，但是最为关注的这两个方向均不超过80%，可以看出在这两个方向上的振动耦合较严重，显然不符合解耦要求。因此，该悬置系统不满足设计要求，需进一步优化。

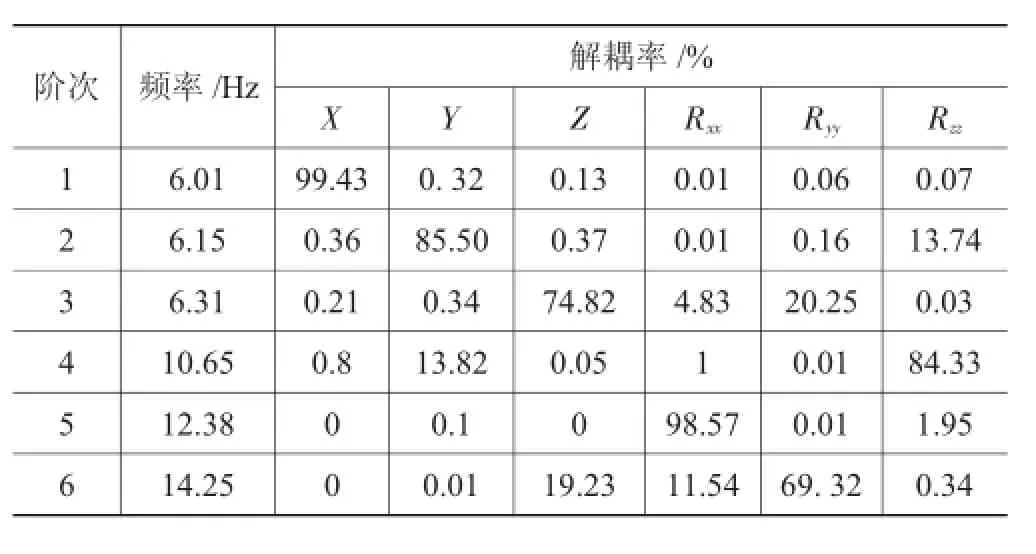
表3　计算结果

2　刚度优化

2.1优化原则

由理论分析可知，悬置系统能量耦合主要源于总成质量惯性耦合和弹性元件弹性耦合；动力总成部件选型已定，质量参数无法修改，优化时暂不考虑；该驱动后桥布局已定型，悬置安装点及安装角度不作考虑。因此，只有从弹性元件入手达到解耦，通过优化协调各悬置轴向刚度参数以满足所有模态的解耦和频率要求。

不同于有标车悬置刚度作参考，可以在初始刚度小范围内寻优。此次公司自主开发的悬置系统仅根据经验设计初始刚度，解耦不理想。

在优化方法上，采用较多的是基于响应面的多因素多目标优化，而解耦率随刚度变动的剧烈敏感性导致响应曲面难以拟合，造成优化结果不可信。复杂的优化算法在工程上推广存在难度，而DOE（Design of Experiment）法简单直观，易于操作；故DOE是一种简单有效的优化方法。根据工程实践的经验，在ADAMS的Design study模块中增加迭代次数，采用逐步逼近的方式易于寻求到满足目标响应的因素组合。

通过前期计算表明，为提高某一方向解耦率改变悬置刚度对动力总成的6阶固有频率影响不敏感，一般均能使固有频率在允许范围内；然而模态振型随刚度变化而阶次变换不定，故可以通过调整悬置刚度来达到设定振型分布阶次。考虑到Z和Ryy向的解耦率要求较高，首先设定其分布阶次。由前述设计目标和仿真分析可以看出，应尽量不使Z向和Ryy向最大解耦率出现在第1阶和第6阶上；于是，合适的阶数分配按优先顺序依次如表4所示。

表4　组合方案

2.2试验设计

以3个悬置共9个轴向刚度为试验因素，其中左悬置刚度设为（LK_X，LK_Y，LK_Z），右悬置为（RK_X，RK_Y，RK_Z），前悬置为（FK_X，FK_Y，FK_Z）。以1-6阶Z向和Ryy向解耦率以及1-6阶固有频率为目标响应。其中各目标响应依次设为OBZ_i，OBRY_i，OBN_i（i=1～6）。考虑到左右悬置Z向刚度不应小于静载变形量5mm时的刚度值；动刚度不宜过大，根据动刚度约为静刚度1.4倍的关系［12］，来确定悬置刚度变化范围上限。前悬置3个方向和左右悬置的X、Y向刚度起非主要承载作用，故增加刚度变量的求解域，以便于实现系统完全解耦。于是，悬置刚度约束范围为:LK_Z和RK_Z分别为216～500 N/mm和221～500 N/mm；其余方向为50～500N/mm。

在Design Study同时优化Z向和Ryy向的解耦率，综合考虑迭代速度和求解精度，设置试验因素水平为200，寻求每个刚度变动时其解耦率的最大值，并代入此时所得某一轴向刚度，继续计算下一轴向刚度，以此类推，完成每个轴向刚度的初始匹配方案；然后按照同样方式，适当修正各向刚度以满足其余4个方向的解耦率；最后关注频率分布。

2.3迭代分析

通过多次反复迭代发现，在约束范围内Case_1和Case_2中Z向和Ryy向解耦率均不符合设计目标，仅有Case_3方案的刚度组合满足要求。其刚度与解耦率关系按照迭代顺序如图3-图5所示，图例中X:OBRY_2表示悬置X向刚度对OBRY_2的影响，其余方向对目标响应与X向表示方式相同。图3表明左悬置轴向刚度对解耦率OBRY_2有显著影响，对解耦率OBZ_4影响不显著。其中，随着X向刚度增加，OBRY_2剧烈增大后并趋于稳定；Y向刚度增加，OBRY_2先趋于稳定后剧烈减小；Z向刚度增加，OBRY_2逐步增大后剧烈减小。左悬置三向刚度增加，使OBZ_4变化不明显。取OBRY_2最大值所对应的刚度值，可暂时依次确定左悬置刚度为（195，50，335）N/mm。图4表明右悬置轴向刚度对解耦率OBRY_2有显著影响，对解耦率OBZ_4影响不显著。其中，X向、Y向刚度增加，OBRY_2和OBZ_4的变化趋势与左悬置类似；随着Z向刚度增加，OBRY_2逐步增大，OBZ_4与之相反。取OBRY_2最大值所对应的刚度值，可暂时依次确定右悬置刚度为（200，50，335）N/mm。图5中表明前悬置X向刚度对两目标无显著影响；Y向刚度只对OBZ_4有作用，并且随着Y向刚度增加，OBZ_4逐步增大后趋于稳定，但对OBRY_2无影响；Z向刚度对两目标影响最为显著，随着Z向刚度增加，两目标剧烈增大到峰值后逐渐减小；暂取前悬置刚度值时，采取不改变X向刚度，增大Y向刚度，并折衷选取Z向刚度，故前悬置刚度值为（106，230，65）N/mm。

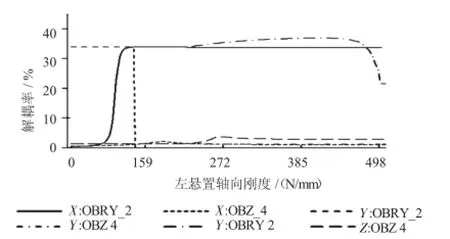
图3　左悬置轴向刚度对解耦率的影响

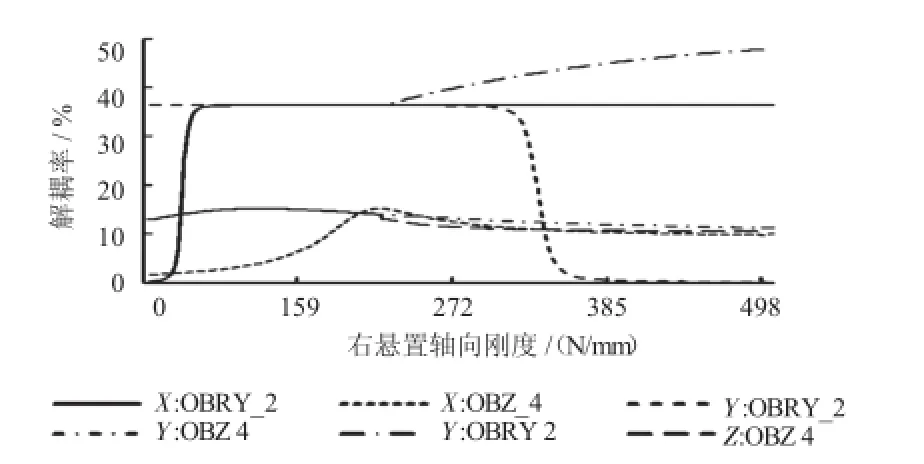
图4　右悬置轴向刚度对解耦率的影响

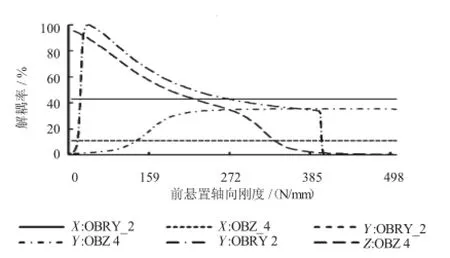
图5　前悬置轴向刚度对解耦率的影响

2.4刚度优化结果

根据上述迭代得到一组刚度值组合，仿真分析发现其它方向解耦率均大于70%；但是第1阶Y向频率偏低，第3阶X向频率与第2阶Ryy向间隔较小；在保证Z向和Ryy向解耦率的前提下，采用同样的方法以悬置刚度对1、3阶固有频率进行迭代，结果表明悬置Y向刚度对第1阶Y向频率影响较显著，即在一定刚度范围内增大Y向刚度具有提高Y向频率的效果；X向刚度亦有类似的效果。参照图3-图5，在X、Y向刚度对Z和Ryy向不敏感段增大刚度。最终优化结果见表5。

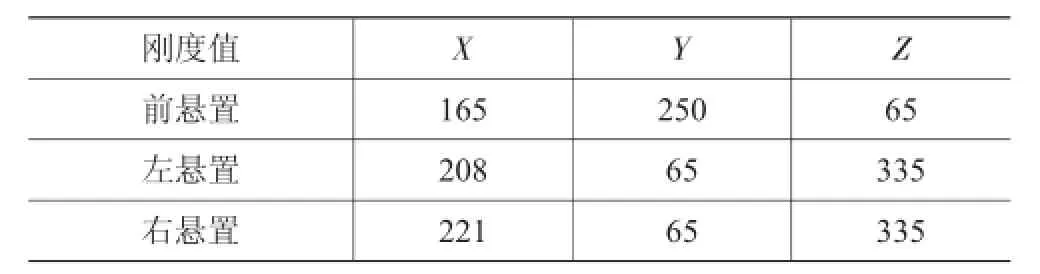
表5　优化后刚度N/mm

将优化后的刚度值代入仿真模型，计算结果如表6所示，可以看出优化后解耦率明显提升；固有频率范围为5.42Hz～16.4Hz，频率间隔基本上大于1，基本满足1.1节中的设计标准。

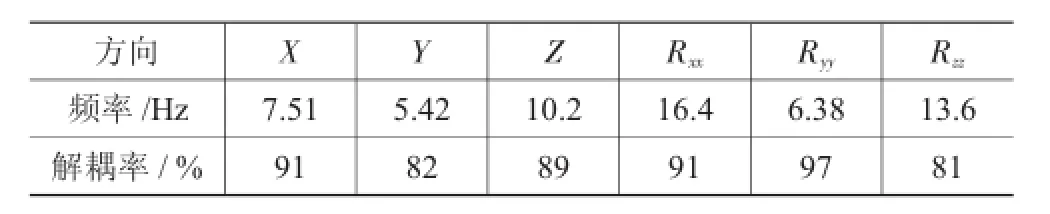
表6　优化后的固有频率和解耦率

3　结论

通过上述分析，可得到以下结论:

1）悬置刚度不但对悬置系统解耦率有显著影响，而且还决定了模态阵型的分布；同时，单个悬置刚度小范围变动对固有频率影响不显著。

2）通过制定优化目标的优先层次和组合方案，选择合适的约束范围和增大设计研究（Design study）中DOE方法的试验因素水平，在经过逐次迭代调整悬置刚度可使该客车悬置系统解耦率达到设计目标的要求。

［1］季晓刚，章应雄，唐新蓬.汽车动力总成悬置研究的发展［J］.汽车科技，2004（1）:4-6.

［2］陈大明，上官文斌.横置动力总成悬置系统的布置设计分析［J］.新技术新工艺，2012（1）:25-28.

［3］徐中明，李晓，刘和平.纯电动汽车动力总成悬置系统的优化［J］.汽车工程，2012，34（9）:806-810.

［4］吕振华，范让林.动力总成悬置系统振动解耦设计方法［J］.机械工程学报，2005，41（4）:49-54.

［5］吴飞，胡朝辉，成艾国，等.综合考虑解耦率和隔振率的发动机悬置系统多目标优化［J］.汽车工程，2013，35（1）:18-22.

［6］陆军.客车发动机悬置系统固有频率选择［J］.机电技术，2005（2）:96-99.

［7］庞剑，谌刚，何华.汽车噪声与振动理论与应用［M］.北京:北京理工大学出版社，2008.6.

［8］李智强.基于频率配置和解耦率的某客车悬置系统优化设计［J］.客车技术与研究，2015，37（6）:9-12.

［9］马山.Audi100轿车液压悬置的隔振机理与实验研究［D］.长春:吉林大学，2002.9.

［10］范让林，吕振华.汽车动力总成三点式悬置系统的设计方法探讨［J］.汽车工程，2005，27（3）:304-308.

［11］李尧尧，王晖.电动汽车动力总成悬置系统优化［J］.重庆交通大学学报:自然科学版，2015，34（1）:135-139.

［12］上官文斌，蒋学锋.发动机悬置系统的优化设计［J］.汽车工程，1992（2）:103-110.

修改稿日期:2016-07-15

Design and StiffnessOptim ization for the Transverse Powertrain Mounting System of a PureElectricalBus

Hu Xiaosheng，Huang Xiang，Dong Zewei
（ShanghaiKomman Vehicle ComponentSystemsCo.，Ltd，Shanghai201815，China）

Theauthorsdetermine themountingposition of the three-pointstyle transversepowertrainmounting system for a pure electric bus，and calculate out the stiffness combination of rubble cushion accord with the decoup ling requirements.Themounting position isconfirmed based on theprincipleof torque rollaxisand the limitation of layout.A dynamicmodel of the powertrainmounting system isestablished by using ADAMS/View to reveal the distribution regularityofnatural frequency and decoupling rate.Then，the DOEmethod isemployed to optimize the rubble cushion axial stiffness so as to further improve the decoupling rate of themounting system.The results indicate that thissystemmeets thedesign goalsand requirements.

pureelectricalbus；transversepowertrain；mountingsystem；design ofexperiment（DOE）；stiffness optimization

U469.72

B

1006-3331（2016）05-0027-04

胡小生（1989-），男，硕士；主要从事客车底盘设计与分析工作。