基于重采样痕迹的图像伪造检测

左菊仙　邓　坚

1(贵州交通职业技术学院信息工程系　贵州 贵阳 550008)2(贵州师范大学求是学院　贵州 贵阳 550001)3(贵州大学计算机科学与信息学院　贵州 贵阳 550025)



基于重采样痕迹的图像伪造检测

左菊仙1邓坚2,3

1(贵州交通职业技术学院信息工程系贵州 贵阳 550008)2(贵州师范大学求是学院贵州 贵阳 550001)3(贵州大学计算机科学与信息学院贵州 贵阳 550025)

检测重采样痕迹是数字取证中判断图像是否被篡改的有效途径之一。针对现有重采样检测方法大多只考虑单次重采样情况，对再次经历重采样的伪造图像不能有效区分定位篡改区域这一问题，提出一种基于重采样痕迹的图像伪造检测算法。首先定义出能够描述并区分不同重采样痕迹的两个特征量，将待测图像重叠分块，计算每块的特征量，然后利用特征量的不一致性检测定位篡改区域。实验结果表明，该方法能够区分旋转与缩放的操作历史痕迹，进行篡改伪造图像的自动判断与篡改区域定位；并且当伪造图像再次经历重采样操作后，仍能区分出图像中的不同插值区域，即对再次重采样操作具有一定的鲁棒性。

伪造检测篡改图像重采样

0　引　言

随着数字图像编辑处理工具的广泛应用，人们可以容易地修改图像内容，同时人眼很难察觉出任何篡改伪造的痕迹。伪造图像大量地充斥互联网和各类媒体，严重地影响了人们的日常生活。而且，伪造图像如果被大量地用于正式媒体、科学发现和法庭证物等，无疑将会对政治和社会稳定产生严重的影响。所以，图像伪造技术为公安侦破和司法取证实战应用带来了新的挑战，鉴别和检测伪造图像的盲取证技术也因此成为当前研究的热点[1]。近年来，许多数字图像盲取证技术已经被提出[2]，这些技术包括重复块检测[3]、模糊估计[4]、JPEG块效应不一致检测[5]等。

在图像伪造过程中，常会伴有缩放和旋转等几何变化，这样的步骤需要运用插值/抽取技术对图像进行重采样，使其位于一个新的采样网格中，所以检测图像重采样技术是图像伪造检测的有效途径之一。目前较成熟的图像重采样检测算法大多是基于以下两个特性：① 重采样信号的二阶差分的统计方差具有周期性[6]；② 重采样操作会导致插值点与其邻域像素点产生一定的相关性[7]。充分利用重采样检测算法并提高其对复杂篡改操作的鲁棒性是图像伪造检测中的一个研究方向。Gallagher[6]利用二阶导数的周期性来分析其幅值和相位的信息，从而估计线性变换。该算法能够检测出缩放操作，但却无法针对旋转操作进行检测，具有一定的局限性。 Wei等[8]在文献[6]的基础上进行扩展，提出了估计旋转因子的算法并应用于图像伪造检测。这些算法大多针对非压缩格式的图片，鲁棒性不强。Zuo等[9]提出一种适用于有损压缩的重采样检测方法，该方法基于重采样和压缩特性定义并提出一种块度量因子，利用块度量因子的不一致性来区分出篡改区域。但当伪造图像以一个较低的质量因子保存时，该算法检测效果不理想。文献[10]提出一种基于再采样的图像重采样检测算法，该算法具有较强的抗JPEG压缩能力。针对篡改图像过程中往往会引入噪声，影响重采样检测及篡改判断，文献[11] 基于重采样操作导致的离散余弦变换(DCT)系数之间相关性的变化，提出了一种新的图像重采样篡改检测方法，该方法对于加噪重采样图像具有一定的鲁棒性。

这些方法主要针对一次重采样操作进行检测。在实际图像篡改伪造过程中，常需要对伪造后的图像再一次进行尺度大小变换，篡改区域与背景区域会同时受到重采样操作的影响，此时针对一次重采样的检测方法将无法区分出篡改区域。基于重采样检测应用于图像伪造检测中的不足，提取能够描述并区分重采样痕迹的两个特征量，利用特征量的不一致性作为检测判断的依据。实验结果表明，该方法能够区分出旋转与缩放的操作历史痕迹，进行篡改伪造图像的自动判断与篡改区域定位；并且当伪造图像再次经历插值操作后，仍能区分出图像中的不同插值区域，检测定位出篡改区域，即对再次重采样操作具有一定的鲁棒性。

1　篡改图像的模型

如图1所示，通常一幅篡改图像是通过从其他原始图像如S中裁剪得到需要的区域R，并将其复制粘贴放置在背景图像T中，从而得到一幅合成图像F。

图1　篡改图像的示意图

从是否经历插值操作的角度来考虑，篡改图像的组合模型可以有4种，如表1所示。现有基于重采样的篡改图像检测方法大多只考虑C1和C2的篡改组合情况，而当篡改区域与背景区域同时经历过重采样操作后，不能较好将篡改区域检测定位出来。考虑到当存在篡改组合C3的情况时，背景区域和篡改区域所经历过的插值因子或者重采样的历史痕迹往往很难保持一致。基于这个前提条件下，本文提出一种基于重采样痕迹的图像伪造检测方法，该方法在篡改组合C1、C2，尤其C3的情况下都将有效。

表1　4种篡改图像的组合模型

注：S1: 经历过重采样操作；S2: 未经过重采样操作

2　基于重采样痕迹的图像伪造检测方法

2.1重采样检测算法

Popescu等在文献[7]中提出插值引入的周期性的相关性是一个简单的线性模型，即插值得到的像素值与其邻域像素值的加权和有关。设f(x, y)是插值图像的像素点，则f(x, y)的取值有两种可能：(1) M1，表示该像素是通过邻域像素插值获得的，与邻域像素值线性相关；(2) M2，表示该像素与周围邻域的像素点不相关，为自然的连续变化，即直接采样获得的像素点。M1用线性模型表示为：

(1)

其中αu,v是线性模型的系数，α={αu,v|-N≤u,v≤N}(N是整数，α0,0=0)，n(x,y)是预测残留误差，服从均值为0，方差δ2为高斯分布。

对线性模型的系数α以及残留误差的正态分布方差δ2，可以用统计方法中的最大似然估计迭代方法来完成。EM算法[12]是解决最大似然估计迭代的良好算法，是一个两步迭代，最终达到收敛的过程。

1) E步，计算每个像素点属于M1和M2的概率。已知f(x,y)属于M1的条件概率可表示为：

Pr{f(x,y)|f(x,y)∈M1}

(2)

由贝叶斯准则可得f(x, y)属于M1的后验概率为：

Pr{f(x,y)∈M1|f(x,y)}

(3)

其中对于直接采样获得的像素点，即M2类，f(x, y)属于M2的条件概率服从均匀分布, 即Pr{ f(x,y)| f(x,y)∈M2}等于f(x,y)取值范围的倒数(实验中取1/256)。先验概率Pr{ f(x,y)∈M1}和Pr{ f(x,y)∈M2}假定为常数，初始设置为0.5。

2) M步，估计像素点之间相关性的具体形式。通过最小化下面的二次误差函数得到新的α：

(4)

(5)

对α中的每个αu,v分别求导，得到(2N+1)2-1个线性方程，对该线性方程组求解就得到新的模型系数αu,v。其中w(x,y)=Pr{f(x,y)∈M1|f(x,y)}。

E步和M步迭代执行，直到α达到稳定。

2.2区分不同的重采样痕迹

使用EM方法得到重采样图像的概率频谱图将存在中心对称的规律亮点，图2显示了对原始图像和重采样图像运用EM算法得到的结果。由实验结果可以看到，没有经过重采样的图像概率矩阵的频谱中不存在规律亮点，而重采样后图像的概率频谱图中存在中心对称的规律亮点。而且不同的重采样痕迹将导致这些规律亮点出现不同的分布。设缩放因子为f，图3显示了六幅不同缩放因子下重采样图像的概率频谱图。由结果可以看到，不同缩放因子会使其对应图像的概率频谱图中的规律性亮点距离中心点的距离不同。设旋转角度为t，图4显示了六幅经过不同旋转角度的重采样图像的概率频谱图。由结果同样可以看到，不同旋转角度会使其对应图像的概率频谱图中的规律性亮点距离中心点的距离和角度各不相同。因此，我们考虑进一步利用距离和角度这两个信息作为检测的特征量，用以区分图像中存在的不同插值区域。

图2　经EM算法处理过的原始图像和重采样图像

图3　经历不同缩放处理后的图像的概率频谱图

图4　经历不同旋转处理后的图像的概率频谱图

首先，我们需要精确定位出频谱图中的规律亮点。设概率频谱图为M(x,y)，为了能准确定位频谱图中的规律性亮点，需将频谱图作如下处理：

1) 置M(x,y)矩阵的中心区域为0，建议中心区域大小在3～5像素之间；

2) 然后用点检测模板B对M(x,y)进行滤波，得到新的矩阵，设为D(x,y)；

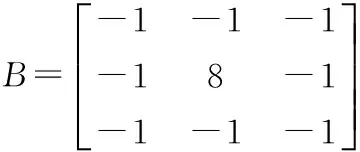
(6)

3) 取出D(x,y)中的最大值，记为Dmax=max(D(x,y))。同时令T=Dmax×k，并进行比较，如果D(x,y)>T，则D(x,y)=1；否则D(x,y)=0。其中k是0～1之间的一个系数。

经过上述预处理操作后，我们可以很容易在D(x,y)得到规律亮点的位置。假设规律性亮点的坐标已知，如图5所示，则定义提取两个特征量r与θ如下：

(7)

其中(x,y)是D(x,y)的中心点坐标，(x1,y1)是分布在D(x,y)第一象限的规律亮点坐标，N是D(x,y)的尺度大小。

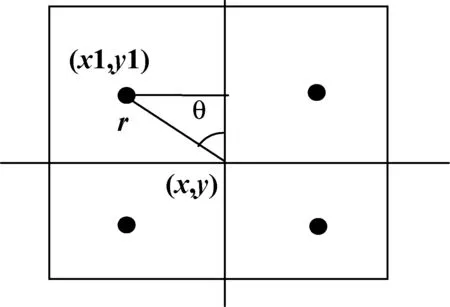
图5　规律亮点的分布示意图

针对图3以及图4中所列出的概率频谱图，分别计算其对应的特征值r和θ，结果如表2、表3所示。由计算的数据可以看到，不同的缩放因子与旋转角度使其特征量r和θ的值各不相同，而且如果图像只经过缩放操作，则对应θ值将为0。由上述讨论可见，依据所提取的两个特征量r和θ可以区分出不同的重采样痕迹，即可以以此来区分背景区域和篡改区域。

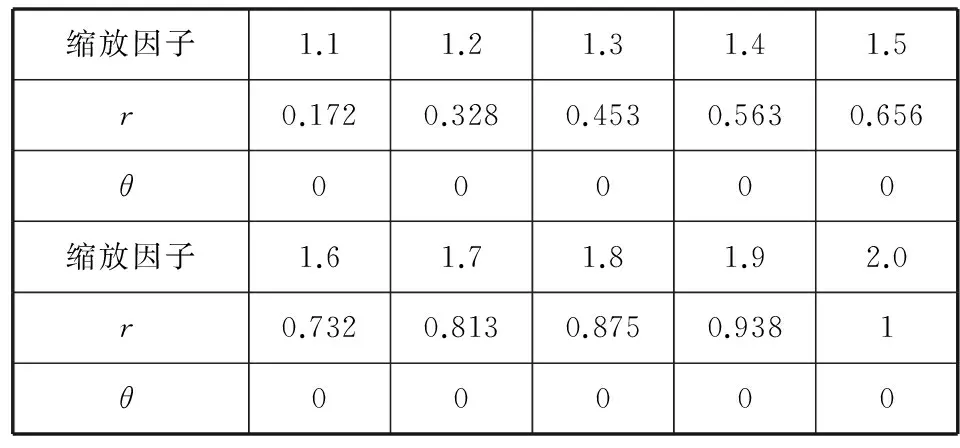
表2　不同缩放图像的r和θ

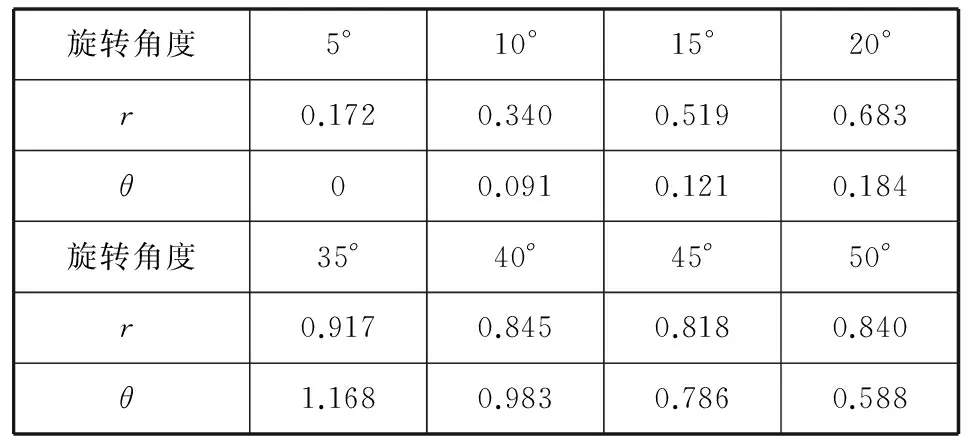
表3　不同旋转图像的r和θ

2.3伪造图像的篡改定位检测

考虑一幅篡改伪造图像，设图像的篡改区域为UT，而背景区域为UA。令rT和θT为篡改区域UT中的特征值，令rA和θA为背景区域UA中的特征值。现分别对表1中的篡改组合C1、C2和C3进行讨论。

1) 对于篡改组合C1，此时满足：

rA=0θA=0

以及

rT≠0θT=0(orθT≠0)

(8)

存在旋转操作时θT≠0，无旋转操作时θT=0，即背景区域与篡改区域可以依据r 和 θ的不同被区分。

2) 对于篡改组合C2，此时满足：

rT=0θT=0

以及

rA≠0θA=0(orθA≠0)

(9)

存在旋转操作时θT≠0，无旋转操作时θT=0，即背景区域与篡改区域仍然可以依据r和θ的不同被区分。

3) 对于篡改组合C3，背景区域和篡改区域同时经历过了重采样操作。此时若能够将这两个区域区分开，必须得满足下列条件，即：

rT≠rAor θT≠θA

(10)

在实际篡改过程中为了视觉上的逼真效果，很难能保证篡改区域与背景区域经历的重采样操作痕迹达到一致，所以使得对篡改组合C3的检测成为可能。设计自动检测步骤如下：

步骤一设待测图像I(x, y)大小为M×N，将其划分成b×b相互重叠的图像块，对于相邻图像块水平或垂直方向相差a个像素点，则待测图像可被分为n=[(M-b)/a+1]×[(N-b)/a+1]个图像块k1,k2,…,kn，块大小最好64×64以上。

步骤二利用EM算法分别计算每一块的概率频谱图，记为P(k1),P(k2),…,P(kn)。

步骤三在频谱图P上分别提取两个特征量r和θ，分别记为r={r(k1),r(k2),…,r(kn)}和θ={k(1),θ(k2),…,θ(kn)}。

步骤四分别统计直方图H(r)=hist(r)以及H(θ)=hist(θ)，根据直方图判断图像是否被篡改，并定位篡改区域。

图6是篡改伪造图像的示意图，其中(a)是一幅原始图像，(b)是对原始图像进行篡改得到的一幅伪造图像。图7显示了对原始图像运用上述算法计算得到的直方图H(r)和H(θ)。从直方图上看，没有出现异常块，即各个块的两个特征量是一致的，则认为其为正常图像。图8显示了篡改图像的直方图H(r)和H(θ)。可以看到，直方图明显被划分为两部分，且可知统计量大的对应背景区域，统计量小的对应篡改区域。检测结果如图8(c)所示，本方法可以准确检测定位出篡改区域，同时从直方图H(r)和H(θ)得知篡改区域经历过缩放和旋转操作。

图6　篡改图像示意图

图7　原始图6(a)的r和θ的直方图

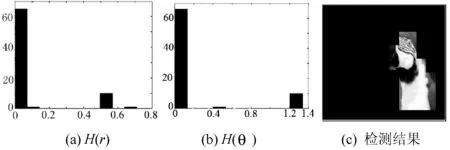
图8　篡改图6(b)的r和θ的直方图以及检测结果

3　进一步分析讨论

本节主要是进一步对篡改组合C3进行讨论，即背景区域和篡改区域同时经历过重采样操作的情况。在篡改过程中，当篡改者需要改变伪造图像的大小、尺度时，可以存在不同的操作顺序，概括起来可以分为两种情况：

第一种情况如图9所示，首先，背景图像A被尺度调整到相应大小的图像A′，设其缩放因子为fA；然后从另一幅图像B中截取所需区域并进行相应的几何变换，设其变换因子为fB，粘贴到图像A′中；最后得到一幅伪造合成图像C。

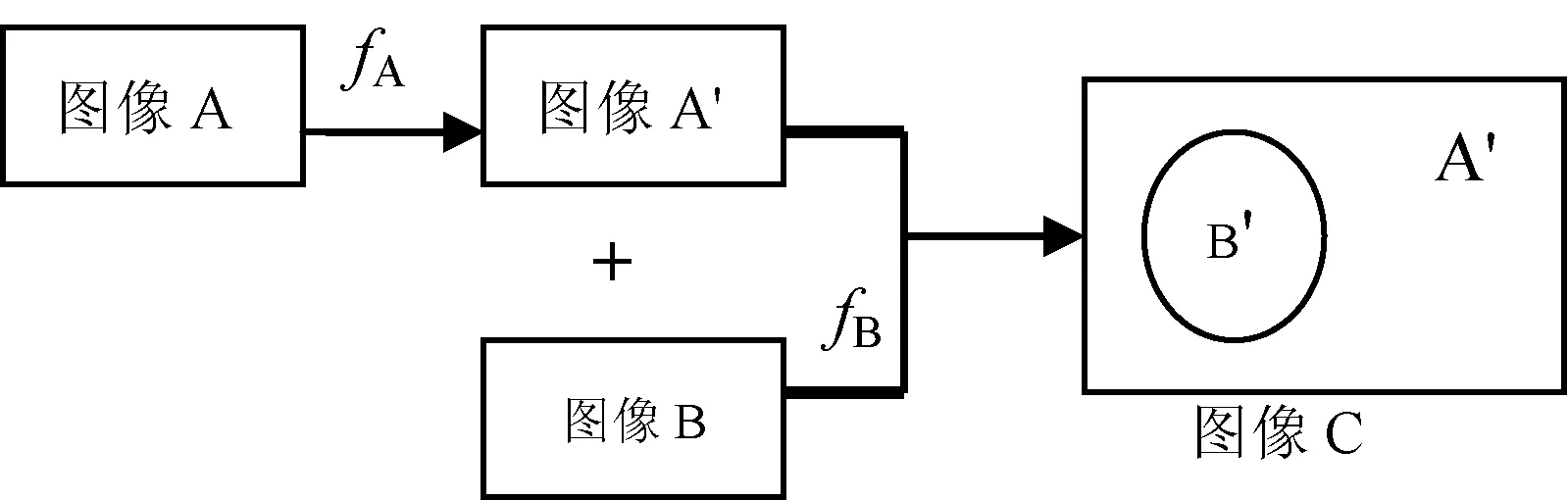
图9　第一种篡改操作顺序的情况

通常在此种情况下变换因子fA和fB很难达到一致，在此条件下可以很容易将篡改区域B′从背景区域A′中区分出来。图10是图像篡改的示意图，其中(a)是一幅原始图像，大小为512×384，然后图像被放大至665×499，得到一幅重采样图像如(b)所示，(c)是另外一幅原始图像。从(c)中裁剪出女孩部分，对其进行相应几何变换，然后粘贴到(b)中，得到一幅篡改伪造图像如(d)所示。运用本文提出的方法对该伪造图像进行检测，结果如图11所示。从r的直方图分布看到出现了小量的异常块，即可推测检测图像中存在不一致的缩放区域；而θ的直方图分布较为一致，即可进一步推测待测图像中的篡改区域没有经过旋转操作或者旋转的角度较小。检测定位的结果如图11(c)所示，可见本文方法能较准确定位检测出篡改的区域。

图10　图像篡改伪造的示意图

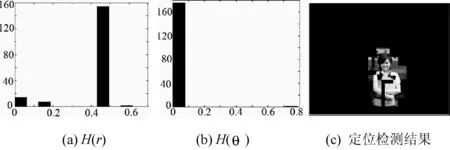
图11　图10(d)的r和θ的直方图以及检测结果

第二种篡改操作顺序情况如图12所示，当得到篡改图像C之后，篡改者可能还需要调整图像的大小、尺度，设其缩放因子为f2。可以看到，在这种情况下篡改区域B′和背景区域A′会经历相同的缩放操作，且缩放因子也相同。此时我们要讨论的问题是在fA和fB不一致的前提下，两个区域再次受到相同的缩放操作，则原来的不一致痕迹是否还保留，即篡改图像C′中的两个区域B″和A″是否能够被正确区分。

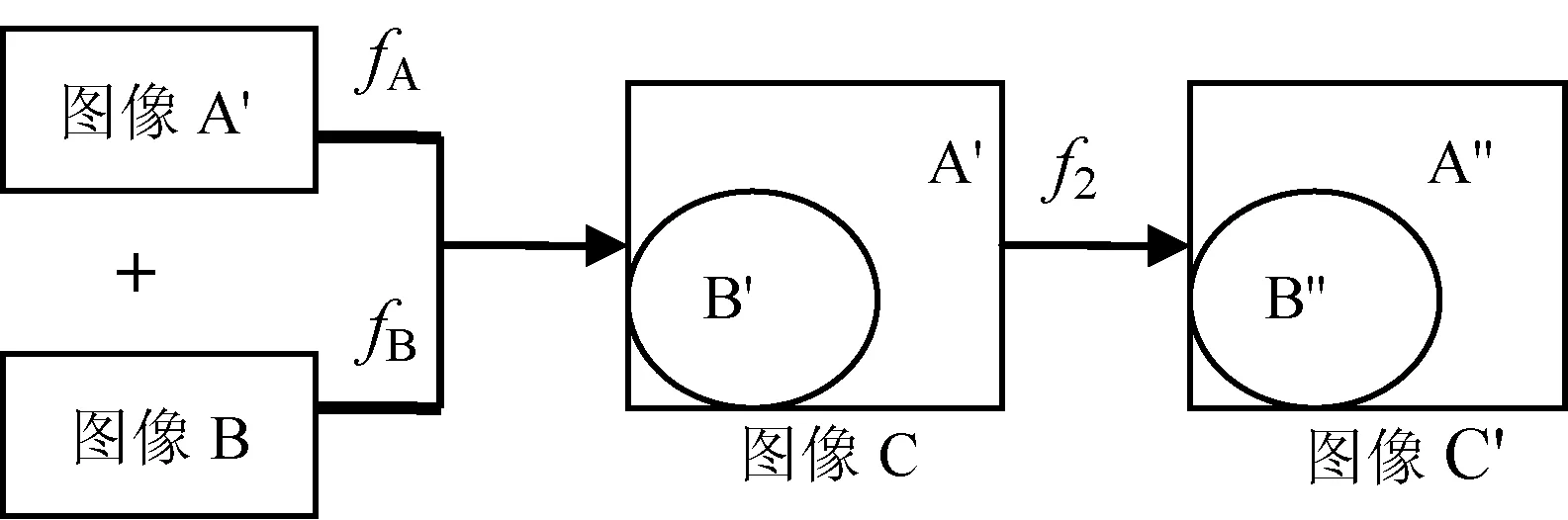
图12　第二种篡改操作顺序的情况

为了验证我们提出的问题，设计10幅重采样图像用于实验讨论，这10幅重采样图像都是从原始图像中进行放大操作得到的。设放大因子为f1，则这10个f1分别为1.1、1.2、1.3、1.4、1.5、1.6、1.7、1.8、1.9以及2.0。然后分别从这10幅重采样图像中裁剪出128×128大小的区域块，计算它们的特征值r，如2.2节中表2所示，可知此时特征值r能够区分不同插值操作。

在图像经历了第一次放大操作之后，接下来我们将继续对上述10幅重采样图像进行再次缩放操作。设其缩放因子为f2，然后得到另外的10幅经历过二次重采样操作的图像。我们同样截取128×128大小的区域块，然后计算它们的特征值r。目的是想观察这些特征值r是否仍保持各不相同的特征，或者由于二次缩放因子f2相同的关系而使得r值保持一致导致无法进行区分。

在本次实验中，我们首先考虑二次缩放操作未放大操作的情况，即f2>1。分别进行三组实验，f2=1.3、1.5和1.8。表4列出了这三组二次重采样图像以及一次重采样图像r值， 从实验数据可以得到以下结论：

只要满足：

fA1≠ fT1

(11)

即使：

fA2=fT2(当 f2>1时)

(12)

仍然满足下述条件：

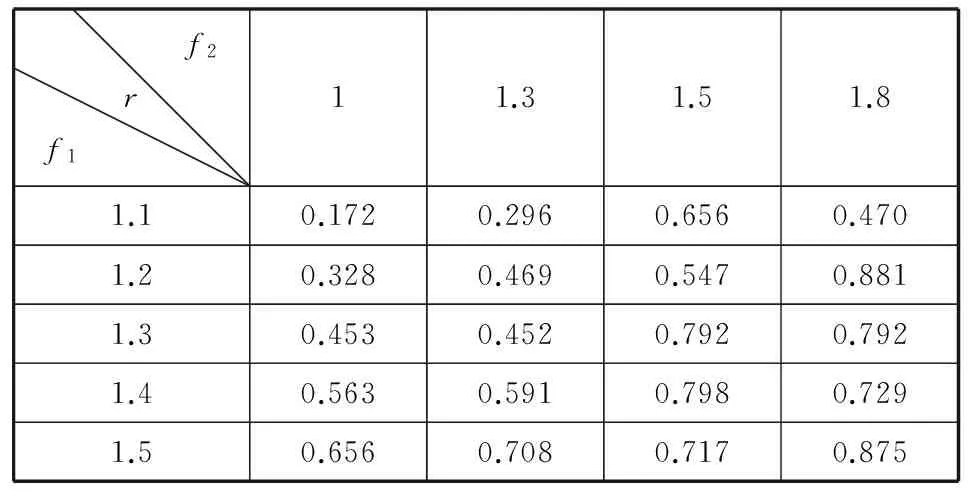
rA≠rT　(13)

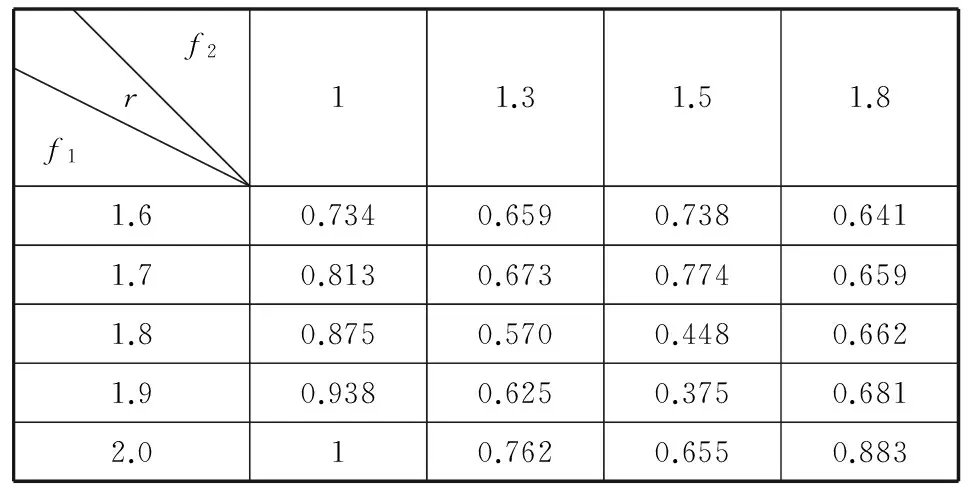
续表4

本文的检测方法在篡改图像被再次整体放大的情况下仍然有效。其中式(11)中fA1和fT1分别代表第一次重采样图像中背景区域与篡改区域的重采样因子，式(12)中fA2和 fT2分别代表第二次重采样图像中背景区域与篡改区域的重采样因子。在上述讨论之后，接下来将讨论尺度缩小的情况，即f<1。首先，我们从原始图像中进行缩小操作得到5幅重采样图像，缩小因子f1=0.9、0.8、0.7、0.6和0.5。然后从这5幅图像中截取不同大小的区域块，分别计算它们的概率频谱图以及特征值r，其r值列于表5。由实验数据可以看到，当图像块为128×128时，只要f1>0.8,本文方法仍然有效，但f1<0.8的情况检测将失效，以至于计算得到的r几乎都为0；当图像块增大至256×256时，只要f1>0.6，本文方法仍然有效，但f1<0.6的情况检测将失效。考虑到本文方法是基于块的检测，而在篡改图像中，篡改区域不会太大，因此检测时所分的图像块不宜太大，以256×256为限。

表5　不同图像的r值

基于上述讨论，我们同样以10幅经历了一次放大操作的重采样图像为实验图，然后对它们分别进行5组不同缩放因子的缩小操作。其中f2=0.9、0.8、0.7、0.6以及0.5，共得到50幅二次重采样图像。它们的r值如图13所示，从实验数据可以得到如下结论：

只要满足:

fA1≠ fT1

(14)

即使:

fA2= fT2f2>0.6

(15)

仍然满足下述条件:

rA≠ rT

(16)

图14是篡改图像示意图，其中(a)和(b)是原始图像，(c)是篡改伪造的图像。然后我们分别对伪造图像14(c)进行再次缩小操作，缩放因子f2=1.3、0.9、0.8、0.7以及0.5，即一共得到六幅篡改图像。分别运用本文提出的方法对该6幅图像进行篡改检测，检测结果如图15所示。实验结果显示，即使篡改图像再次受到缩小操作，本文方法仍然在一定程度上是有效的，但当二次缩放因子逐渐减小时，检测能力也逐渐减弱，这是本文方法的一个缺陷。

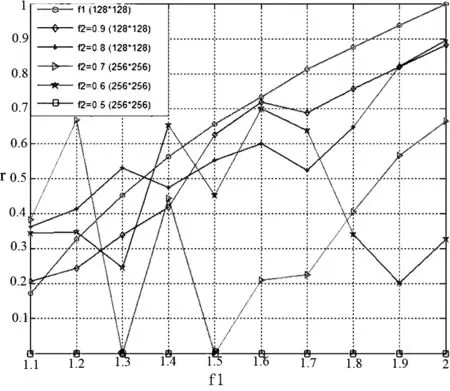
图13　50幅二次重采样图像的r值

图14　篡改伪造示意图

图15　图14(c)的r的直方图和检测结果

4　结　语

基于重采样检测应用于图像篡改检测中的不足，本文利用EM方法得到重采样图像的概率频谱图，并在此基础上进一步利用规律性亮点的位置信息，定义能够描述并区分重采样痕迹的两个特征量；将图像重叠分块，计算块特征量，利用特征量的不一致性来检测定位篡改区域。实验结果表明，该方法能够准确区分出旋转与缩放的操作历史痕迹，进行伪造图像的自动判断与篡改区域定位；并且当伪造图像再次经历重采样操作，该方法仍能区分出不同插值区域，即对再次重采样操作具有一定的鲁棒性。然而对于缩放因子小于0.5的情况，检测定位篡改区域的错误率将增高，这是下一步有待研究和改进的课题。

[1] Luo W Q,Qu Z H,Pan F,et al.A survey of passive technology for digital image forensics[J].Frontiers of Computer Science in China,2007,1(2):166-179.

[2] Farid H.Image forgery detection:A survey[J].IEEE Signal Processing Magazine,2009,26(2):16-25.

[3] 徐彩臣,孙锐,李涛.一种新颖的数字图像复制粘贴篡改被动取证算法[J].仪器仪表学报,2011,32(12):29-33.

[4] 杨本娟,左菊仙,刘本永,等.基于像素线性相关性检测的篡改模糊检验[C]//2010年全国模式识别学术会议论文集,重庆,2010:158-162.

[5] 左菊仙,刘本永.伪造图像典型篡改操作的检测[J].中国图象图形学报,2012,17(11):1367-1375.

[6] Gallagher A C.Detection of linear and cubic interpolation in JPEG compressed images[C]//Computer and Robot Vision,The 2nd Canadian Conferenceon,2005:65-72.

[7] Popescu A C,Farid H.Exposing Digital Forgeries by Detecting Traces of Re-sampling[J].IEEE Transactions on Signal Processing,2005,53(2):758-767.

[8] Wei W M,Wang S Z,Zhang X P,et al.Estimation of image rotation angle using interpolation-related spectral signatures with application to blind detection of image forgery[J].IEEE Transactions on Information Forensics and Security,2010,5(3):507-517.

[9] Zuo J X,Pan S J,Liu B Y,et al.Tampering detection for composite images based on re-sampling and JPEG compression[C]//Proceedings of the First Asian Conference on Pattern Recognition.Piscataway,NJ: IEEE Press,2011:169-173.

[10] 刘一,刘本永.基于再采样的图像重采样伪作检测[J].计算机应用,2014,34(3):815-819.

[11] 周治平,胡成燕,朱丹.基于Markov过程和伪极坐标快速傅里叶变换的重采样篡改检测[J].计算机应用,2014,34(11):3323-3326,3331.

[12] Dempster A,Laird N,Rubin D.Maximum lilelihood from incomplete data via the EM algorithm[J].Journal of the Royal Statistical Society,1977,99(1):1-38.

IMAGE FORGERY DETECTION BASED ON RESAMPLING TRACES

Zuo Juxian1Deng Jian2,3

1(DepartmentofInformationEngineering,GuizhouJiaotongCollege,Guiyang550008,Guizhou,China)2(QiushiCollege,GuizhouNormalUniversity,Guiyang550001,Guizhou,China)3(CollegeofComputerScienceandInformation,GuizhouUniversity,Guiyang550025,Guizhou,China)

To detect resampling traces is one of the effective ways in digital forensics to determine whether or not the image has been tampered. Existing resampling detection methods mostly consider the single resampling cases only but cannot effectively differentiate and locate the tampered region on the forged image with secondary resampling. Aiming at this problem, we propose in this paper a resampling trace-based algorithm for image forgery detection. We first give the definition on two feature values capable of describing and differentiating different resampling traces, and then overlap and divide into blocks the measuring images to calculate the feature value of each block, and use the inconsistency of feature values to locate the tampered regions. Experimental results show that the algorithm is able to distinguish historical traces of rotation and scaling operations, to make automatic determination on tampered and forged images and localisation of tampering region. Moreover, when the forged image comes through resampling operation once again, it can still differentiate different interpolation regions in the image, i.e. it has certain robustness on secondary resampling operation.

Tampering detectionForged imageResampling

2015-05-11。左菊仙，助教，主研领域：数字图像处理。邓坚，硕士生。

TP391.41

A

10.3969/j.issn.1000-386x.2016.10.073