实现多目标优化的机场特种车辆调度算法

衡红军　晏晓东

(中国民航大学计算机科学与技术学院　天津 300300)



实现多目标优化的机场特种车辆调度算法

衡红军晏晓东

(中国民航大学计算机科学与技术学院天津 300300)

为保证航班正常运行，机场特种车辆必须高效完成地面保障服务任务。目前机场特种车辆的调度方式是单车单航班服务的人工调度方式，成本较高，且效率较低。针对该问题提出一种基于节约算法的解决方案。该方案分为两个阶段：第一阶段，利用节约算法求出满足行驶总路程最短的子路径集合；第二阶段，通过构建的新方法将每个子路径任务合理分配给所有车辆，实现车辆数目最少和任务量差异最小的目标。以国内某机场实际航班数据做算例进行实验，与单车单航班服务相比，总路程节省49.28%；与不加任务量约束相比，任务均衡度由43.55%提高到95.16%。实验结果表明，利用该算法调度特种车辆可大幅降低服务成本，且能实现任务均衡。

机场特种车辆调度节约算法任务均衡多目标优化

0　引　言

航班在机场过站期间需要接受清洁、配餐、加水、燃油加注、装卸行李货物等一系列地面保障服务。这些服务主要通过一些不同类型的特种车辆(如清洁车、配餐车、加油车、行李车等)来完成。车辆调度方案的优化对提高航班正点率和资源利用率至关重要。目前我国民航机场对特种车辆的调度大都是依靠人工调度，即单车单航班服务。这种低效率的调度方式往往导致车辆利用率不高，而且是造成航班延误的重要因素。

机场特种车辆调度问题实质上是一种车辆路径问题VRP[1,2]。每个航班都有接受地面服务的需求。管理者需要组织合理的行车路线，使得每个航班的需求得到满足，并能在一定的约束(车辆续驶路程、车辆载运量、航班时间窗等)下，达到路程最短、所需车辆最少、车辆任务量差异最小等目的。根据以往研究，解决此类问题以启发式算法为主。如文献[3,4]介绍了粒子群算法解决车辆路径问题，文献[5-7]利用各种改进遗传算法解决多约束条件下的车辆路径问题，文献[8,9]将蚁群算法应用于此类问题，而文献[10]联合使用遗传算法和蚁群算法来解决物流配送中的车辆路径问题。

虽然解决此类问题的方法较多，但机场特种车辆调度问题具有其特殊性：一是航班对服务质量要求较高，不允许保障车辆造成航班延误，只能采用硬时间窗[11]约束(特种车辆必须在规定时间段内完成保障任务)；二是对于大部分机场，进出港航班不够密集，相邻航班时间间隔较大(相对航班过站时间)，这对那些通过逐步选点来搜索最短路径的算法影响较大(因为待选点往往不能满足时间窗约束，这也是本文算法在解决该问题时无法在相同约束条件下与其他算法进行对比的原因，只与人工调度方式进行对比)。而节约算法[12]通过回路合并的方式搜索最短路径，合并过程中即时更新回路中所有航班的服务时刻点，较适合解决此问题。并且联合本文构建的新方法使用时，可实现多目标优化，实用性较强。

本文所做的工作是：首先，以燃油加注服务为研究对象，根据其业务特点建立机场加油车调度的数学模型；然后，利用节约值算法求出满足加油车续驶路程和航班时间窗约束的最优子路径集合；最后，通过本文构建的新方法将所有子路径任务合理分配给加油车，既节省加油车数量，又考虑了加油车的任务均衡性。

由于本文方法是将整个问题分为两个阶段解决，独立优化总路程最短、任务均衡及车辆最少等目标，所以，实现负载均衡的同时并不会以增大总路程为代价。与2006年但正刚等人[13]提出的实现负载均衡的算法相比，本文方法更具优势。该方法同时也适用于配餐、加注清水等地面服务的特种车辆调度，只需根据实际情况调整约束条件(如最大续驶路程、时间窗规则及载运量等等)。

1　问题描述和数学模型

机场加油车是一种为航班提供燃油服务的车辆。机场铺设有地下油管，连系到各个泊位下，飞机只须通过泵车加油。因此，与普通车辆路径问题不同，该问题只有最大续驶路程和航班时间窗约束，而没有最大载运量约束。

给定n个航班F={1,2,…,n}，l辆汽车V={1,2,…,l}，机场加油车最大续驶路程为Q。设计每辆加油车的行驶路线，每条行驶路线可能包含多个子路径，要求满足如下约束：每个航班恰好被服务一次；每条子路径起始于加油车车场(编号：0)，终止于加油车车场(编号：n+1)，记N={0,1,…,n+1}；每条子路径的行驶路程不能超过加油车的最大续驶路程；每个航班必须在其时间窗[ai,bi]内被服务，否则会导致加油车等待或延迟服务。最终目标通常有三个：使所用的加油车数目最少；使所有加油车走过的总路程最短，使每辆加油车之间的任务量差异最小(即任务均衡度最大)。

参数定义：

Ti表示航班i需要的加油服务时间。

dij表示加油车从航班i所在停机位到航班j所在停机位的行驶距离。

sik表示加油车k开始为航班i服务的时间，令s0k=0；如果加油车k没有为航班i服务，则sik没有任何意义，k∈V。

ai表示时间窗下限。

bi表示时间窗上限。

数学模型表示为：

(1)

(2)

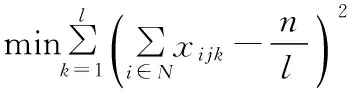
(3)

(4)

(5)

(6)

(7)

(8)

sik+Ti+tij-ω(1-xijk)≤sjk∀i,j∈N∀k∈V

(9)

ai≤sik≤bi∀i∈N∀k∈V

(10)

xijk∈{0,1}∀i,j∈N∀k∈V

(11)

在上述表达式中，式(1)表示使所有加油车走过的路程最短；式(2)表示使需要的加油车数目最少；式(3)表示使每辆加油车之间的任务量差异最小；式(4)表示每个航班仅能被访问一次；式(5)表示被调用的加油车都满足最大续驶路程要求；式(6)-式(8)保证每辆加油车从出发点出发，访问客户后，最终回到出发点；式(9)表示加油车k在从航班i向航班j行驶的过程中，在时间sik+Ti+tij之前不能到达航班j，其中ω是一个较大的标量，若xijk=0则可保证式(9)的约束一定成立；式(10)表示加油车为航班i服务的时间必须在其时间窗口内；式(11)是整数化约束。

该问题的解可以用一个整数序列表示。例如，假设有10个航班，它的一个解可以表示为整数序列{0 1 6 5 0 2 3 4 0 8 7 10 9 0}，其中R1={1,6,5}表示第一条路径，R2={2,3,4}表示第二条路径，R3={8,7,10,9}表示第三条路径[14]。然后，在满足时间要求前提下进行任务分配，第一辆加油车按照R2、R1路径的顺序为航班服务，第二辆加油车按照R3路径为航班服务。

2　节约算法原理及算法设计

2.1节约算法原理

核心思想：依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直至达到一辆车的最大续驶路程；再进行下一车辆的优化，直到所有客户的需求全部满足。

由节约算法[15]，得到：

S(i,j)=di0+d0j-dij

(12)

即为把点i和点j连接在一起时相比i和j单独各在一条线路上的路程节约值。在连接点对时，需考虑车辆的续驶路程约束和时间窗约束。

以EFj表示连接点i和点j所在的线路后，车辆到达j点的时间相比原线路上j点任务的开始时间的推迟(或提前)量，则EFj可由下式得到：

EFj=si+Ti+tij-sj

(13)

显然，EFj<0时，j点任务的开始时间提前；EFj=0时，开始时间不变；EFj>0时，开始时间推迟。

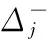
(14)

(15)

2.2算法设计

具体步骤：

(1) 计算S(i,j)，令M={S(i,j)|S(i,j)>0}，并将M按S(i,j)从大到小进行排序。

(2) 令U={1,2,…,n}，表示待选顾客点集合。

(3) 若M=φ，则转步骤(7)；否则对M内第一项S(i,j)，考察对应的i、j，若满足以下条件之一：

① 点i和点j均不在已构成的线路上；

② 点i或点j在已构成的线路上，但不是线路的内点(即不与车场相连的点)；

③ 点i和点j位于已构成的不同线路上，均不是内点，且一个是起点，一个是终点。

转下一步，否则转步骤(7)。

(4) 考察点i和点j连接后的子路径行驶总路程q，若q≤Q，则转下一步，否则转步骤(7)。

(5) 计算EFj：

① 若EFj=0，则转步骤(6)；

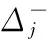
(6) 连接点i和点j，U=U-{i,j}，转步骤(7)。

(7) M=M-S(i,j)，转步骤(3)；若U=φ，则终止，否则将剩余待选顾客点分别安排子路径，即终止。

3　任务分配均衡性及其具体实现

虽然节约值算法找出了使总路程最短(即优化第一目标，式(1))的子路径集合，但在安排加油任务时，同一辆加油车在不同时刻可以重复利用，即一辆车在不同时刻可以完成多个子路径的加油任务。因此，为了使所需车辆数目最少(即优化第二目标，式(2))和使每辆加油车之间的任务量差异最小(即优化第三目标，式(3))，还需将所有子路径任务合理分配给每一辆加油车。

3.1任务分配均衡性

为加油车分配子路径任务又是一个组合优化问题，分配时要满足两个约束：一是同一辆车所分配的子路径任务间在时间上不能重合；二是尽量考虑每辆车的任务均衡性。以服务航班数量总和来衡量每辆加油车任务量的大小；同时，本文提出任务均衡度的概念，来衡量总体任务均衡性。

参数定义：

θ：任务均衡度；

l：总车辆数；

Ci：第i辆加油车的总任务量(单位：航班数)；

Ctotal：总加油任务量(单位：航班数)；

以下式表示任务均衡度：

(16)

为达到各加油车任务均衡的目的，分配任务时需遵循两个原则：一是开始服务时间早优先原则，即子路径任务开始时间越早，越优先被分配；二是对每辆车加上任务量约束，设定一个阈值λ(单位：航班数)，为每辆车分配加油任务时任务量均不应超过λ。

3.2具体实现

具体步骤：

(1) 根据子路径方案R={R1,R2,…,Rs}，计算Ri的开始服务时刻tstart(i)和结束服务时刻tend(i)，i∈{1,2,…,s}。

(3) 将R的前l个子路径任务分别分配给这l辆车，作为它们的第一个子路径任务。

(4) 依次为这l辆车分配任务：找出当前为该车分配的最后一个子路径的tend(i)，在所有满足tstart(j)>tend(i)的待分配子路径中找出一个tstart(j)最小的作为该车下一个子路径任务，直到不存在满足tstart(j)>tend(i)的待分配子路径为止。

(5) 若分配完毕后还有子路径任务未被分配，l=l+1，转步骤(3)；否则，至少需要l辆加油车才能完成所有加油任务，转步骤(6)。

(6) 按照上一步的l值，加上任务量λ约束，重复步骤(3)、步骤(4)。若分配完毕后仍有子路径任务未被分配，λ=λ+1，转步骤(6)；否则，算法终止。

4　算例分析

本文采用国内某机场的航班数据做算例，实现对机场加油车的调度，验证该算法的有效性。

4.1数据采集

该机场拥有客机停机位63个，每天进离港航班大约300架次。规定飞机加油车行驶速度为20 km/h，加油车最大续驶路程为50 km[16]。由于加油车一定会对离港航班进行加油服务，本文只选取该机场2014年9月4日00:00:00到2014年9月5日00:00:00之间的所有离港航班(124个)进行实验，解决机场加油车辆调度问题。

4.1.1机型大小

由于不同类型飞机所需加油量和加油服务时间不同，所以必须对飞机进行分类，大概分为三类：小型飞机、中型飞机、大型飞机[17]。表1是不同类型飞机的载客量、燃油需求量、加油服务时间、过站时间。

表1　不同类型飞机的加油需求量和服务时间

4.1.2停机位距离

与普通物流车辆调度相比，机场加油车调度具有其特殊性，主要表现在车辆行驶路线上。在机场，特种车辆必须按照规定的路线(如图1中路线)行驶，不得进入飞机行驶区域。

该机场现有63个客机停机位，分布于三个区域：远机位、T1航站楼、T2航站楼(如图1所示)。根据其邻接关系，编号依次为：409、410、411、412、413、414、415、416、417、418、419、101、102、103、104、105、106、107、108、109、501、502、503、504、110、111、112、113、114、115、116、117、118、201、202、203、204、205、206、207、208、209、210、211、212、213、214、215、216、217、218、219、220、221、222、223、224、225、226、227、228、229、230。其中加油车车场位于停机位109和停机位501之间，其邻接关系由其位置决定，相邻停机位之间距离大约40米。表2列出了车场(编号：D)和其中8个停机位任意两点之间的距离(单位：米)。

图1　该机场停机位布局示意图

D106107108109501502503504D016012080404080120160106160040801202002402803201071204004080160200240280108808040040120160200240109401208040080120160200501402001601208004080120502802402001601204004080503120280240200160804004050416032028024020012080400

4.1.3离港航班时间窗

时间窗即由服务车辆开始为该航班服务的最早开始服务时间(或称时间窗下限)和最晚开始服务时间(或称时间窗上限)限制的时间范围。服务车辆必须在这个时间范围内开始为该航班服务，否则可能导致航班延误。

民航局规定[16]：加油车应在旅客开始登机前5分钟完成加油服务，载客加油或特殊情况下加油应在预计离港时间前5分钟完成。即加油车必须至少在预计离港时间前5分钟完成加油服务。

下面根据该机场的计划离港时间数据，确定其时间窗下限和时间窗上限。

参数定义：

ai：时间窗下限；

bi：时间窗上限；

td：计划离港时间；

Ttotal：过站时间；

Ti：加油车服务时间。

离港航班时间窗：

ai=td-Ttotal

(17)

bi=td-Ti-5

(18)

按照式(17)和式(18)得到的部分离港航班时间窗如表3所示。实际处理时间参数时，均将24进制转化为10进制，单位为分钟。

表3　离港航班时间窗(部分)

4.2结果分析

通过Matlab编程实现本文算法，并将其应用于该机场加油车调度问题，得出了124个离港航班接受加油车服务的开始时间、结束时间及每辆加油车的路径安排方案。

4.2.1航班接受加油服务的时间段

本文算法采用硬时间窗约束，最后得出的调度结果中开始服务时间均在时间窗内，加油车不会造成航班延误。以航班为对象，表4列出了部分航班接受加油服务的时间段。

表4　离港航班接受加油服务时间段(部分)

4.2.2子路径方案

下面，以子路径为对象，表5显示了本文算法产生的子路径方案，一共产生44个子路径。这意味着在24小时内不同时刻需要44个车次来完成所有加油任务，而传统单车单航班服务方式，则需要124个车次。

表5　产生的子路径方案(全部)

续表5

按照本文调度结果安排加油车路径时，车辆总路程为44.8 km，而单车单航班服务方式总路程为88.32 km。与其相比，本文算法节省了49.28%的路程，大大降低了加油服务成本。

4.2.3加油车任务分配

下面，以加油车为对象，为每一辆车分配加油任务。先不考虑任务均衡性，即分配任务时不对每辆加油车加任务量λ约束。表6列出了不考虑任务均衡性时加油车的路径调度方案。

表6　加油车任务分配方案(全部)

由表6可以看出，仅按照开始时间早优先分配原则，而不加任务量约束时，其任务均衡度(根据式(16)计算)为43.55%，每辆加油车间的任务量差异较大，仍需调整。下面，利用本文构建的新方法为每辆车分配任务时加上λ约束，结果如表7所示。

表7　均衡调整后的分配方案(全部)

通过以上加油任务分配，完成所有航班加油任务仅需4辆加油车，极大节省了加油车资源；并且将任务均衡度提高到95.16%，大大缩小了每辆加油车间的任务量差异。

5　结　语

本文将机场加油车调度问题建立数学模型，利用节约值算法得出使总路程最短的子路径集合，然后通过本文构建的新方法将所有子路径任务合理分配给加油车。为避免因加油服务造成航班延误，本文采用硬时间窗约束，使每个航班一定会在规定时间内得到加油服务。最终，本文解决方案能同时优化三个目标函数，并成功应用在机场加油车调度问题上。

该算法也有其局限性，例如，如果航班计划受天气、其他地勤服务等不确定因素影响而改变，加油车调度方案也应根据实际情况快速做出调整。而本文给出的是一个静态调度方案，后期需对动态调度做进一步研究，以增强整个算法的鲁棒性。

[1] Dantzig G B,Ramser J H.The truck dispatching problem[J].Management Science,1959,6(1):80-91.

[2] 侯玉梅,贾震环,田歆,等.带软时间窗整车物流配送路径优化研究[J].系统工程学报,2015,30(2):240-250.

[3] 高晓巍.基于改进QPSO算法的物流运输路径问题研究[J].计算机仿真,2013,30(8):169-172.

[4] 张耀军,谌昌强.基于改进量子PSO算法的可约束车辆路径优化[J].计算机测量与控制,2014,22(9):2875-2878.

[5] 李锋,魏莹.求解随机旅行时间的C-VRP问题的混合遗传算法[J].系统管理学报,2014,23(6):819-825,831.

[6] 李华,赵冬梅,崔国成.具有模糊可选时间窗的VRPSPD问题及其混合遗传算法[J].物流技术,2013,32(5):315-318.

[7] 葛显龙,王旭,代应.基于混合量子遗传算法的随机需求车辆调度问题[J].系统工程,2011,29(3):53-59.

[8] 徐毅,李章维.蚁群算法在电力巡检路线规划中的应用[J].计算机系统应用,2015,24(5):135-139.

[9] 费腾,张立毅,孙云山.基于DNA-蚁群算法的车辆路径优化问题求解[J].计算机工程,2014,40(12):205-208,213.

[10] 陈印,徐红梅.混合算法在车辆路径优化问题中的应用[J].计算机仿真,2012,29(5):356-359.

[11] 王莲花,彭鑫.带时间窗的配送车辆路径问题模型及算法[J].物流技术,2015,34(3):95-97,238.

[12] 李军.有时间窗的车辆路线安排问题的启发式算法[J].系统工程,1996,14(5):45-50.

[13] 但正刚,蔡临宁,杜丽丽,等.车辆路径优化问题的均衡性[J].清华大学学报:自然科学版,2006,46(11):1945-1948.

[14] 刘小兰,郝志峰,汪国强,等.有时间窗的车辆路径问题的近似算法研究[J].计算机集成制造系统,2004,10(7):825-831.

[15] Doyuran T,Catay B.A robust enhancement to the Clarke-Wright savings algorithm[J].Journal of the Operational Research Society,2011,62(1):223-231.

[16] 中国民用航空局.航空公司航班正常运行标准(试行)(民航发[2013]83号)[S].北京:民航局综合司,2013.

[17] 樊琳.大型机场地勤服务中的车辆调度问题的初步研究[D].沈阳:东北大学,2009.

IMPLEMENTING AIRPORT SPECIAL VEHICLES SCHEDULING ALGORITHM WITH MULTI-OBJECTIVE OPTIMISATION

Heng HongjunYan Xiaodong

(CollegeofComputerScienceandTechnology,CivilAviationUniversityofChina,Tianjin300300,China)

In order to ensure normal operation of flights, airport special vehicles have to accomplish ground support services efficiently. Current scheduling method for special vehicles is the artificial method in which one car services one flight only, it has high cost and low efficiency. Aiming at this problem, we put forward a saving algorithm-based solution. The solution has two steps. First, we calculated the subpath set satisfying shortest total driving distance with saving algorithm. Secondly, we assigned each subpath task to all vehicles reasonably by the new constructed method to achieve the goal of least vehicle number and smallest load difference between vehicles. Experiments have been carried out using actual flights data as the numerical example in a certain domestic airport. Compared with the service in one-car-one-flight way, the total driving distance saved 49.28%; and compared with the method without load restriction, the load balancing degree increased from 43.55% to 95.16%. Experimental results showed that to apply this algorithm in special vehicle scheduling can greatly reduce the service cost, and realise the load balance as well.

Airport special vehicle schedulingSaving algorithmLoad balanceMulti-objective optimisation

2015-06-27。国家自然科学基金项目(U1333109)。衡红军，副教授，主研领域：智能决策支持。晏晓东，硕士生。

TP301

A

10.3969/j.issn.1000-386x.2016.10.053