基于支持度和自适应加权的MEMS陀螺信息融合算法
孙田川,刘洁瑜
(火箭军工程大学控制工程系,西安710025)
基于支持度和自适应加权的MEMS陀螺信息融合算法
孙田川,刘洁瑜*
(火箭军工程大学控制工程系,西安710025)
针对MEMS陀螺阵列进行信息融合可以大幅提高其测量精度和可靠性,而传统信息融合算法大部分依赖于观测信息的先验知识而受到应用上的限制。在不依赖于先验知识的基于支持度的融合算法的基础上,提出一种新的加权系数构造方法,利用自适应加权法的思想改变各个传感器观测值方差对权系数的影响程度,既保证了阵列输出结果的可靠性,又能使融合后得到目标参数的总方差最小;而且自适应加权算法中,对各个传感器方差的计算考虑到环境因素等带来的噪声,与各传感器方差的真实值更加接近。实验结果表明,本文提出的融合算法优于传统的平均值估计融合算法和支持度融合算法。
MEMS陀螺阵列;信息融合;支持度融合;自适应加权
EEACC:doi:10.3969/j.issn.1004-1699.2016.10.014
伴随着微机械技术和微电子技术的发展,MEMS陀螺仪成为当前的研究热点之一。与传统陀螺仪相比,硅微机械陀螺仪具有体积小、重量轻、成本低等优点[1-3],但存在准确度低、噪声大等缺点,单独长时间使用误差积累较大,而通过对多个MEMS陀螺的信息融合可以降低由此造成的系统不确定性并提高系统精度和可靠性[4-6]。
从含有噪声的传感器量测数据中估计目标参数的融合方法很多,文献[7]中提出一种基于最小二乘法的冗余信息数据融合算法;文献[8]利用HHT方法融合硅微阵列陀螺的静态漂移信号,增强了其零偏稳定性;然而这些方法都要求观测信息先验知识已知,当先验知识未知时,目前没有较好的方法。
本文将自适应加权估计和不依赖于先验知识的基于支持度的融合算法相结合,提出一种新的加权系数构造方法,利用这种方法对MEMS陀螺阵列输出数据进行信息融合,实验结果表明,本文提出的融合算法优于传统的平均值估计融合算法和基于支持度的融合算法。
1 基于支持度的信息融合算法
由n个传感器组成的阵列,采用直接测量的方法,对静止或渐变参数X检测,即:

式中:zi(k)为第i个传感器在k时刻的观测值,X为目标,vi(k)为k时刻的观测噪声,且E[vi]和D[vi]均未知。
如果zi(k)和zj(k)相差较大,表明这两个传感器的观测值相互支持度较低,甚至相互背离;如果zi(k)和zj(k)很接近,表明这两个传感器的观测值相互支持度高。定义多传感器测得数据间的这种支持度为互支持度[9]。
为量化各传感器同一时刻观测值的支持程度,引入指数衰减函数并构造支持度矩阵,运用指数衰减函数量化传感器观测值的支持程度,避免了传统方法支持度非0即1的绝对性。另外t为可调参数,程序上易于实现。
k时刻传感器i和传感器 j观测值支持度为
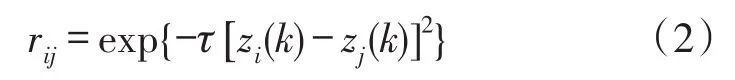
式中,t为可调参数。通过调节t的大小,可以方便调节度量尺度。
由式(2)可得k时刻传感器间的支持度矩阵

为了反映zi被其它n-1个传感器观测值的综合支持程度,定义了一个综合支持度函数si

si的大小反映了zi被其他传感器综合支持程度的高低。
定义k时刻第i个传感器观测值与其它n-1个传感器观测值一致性度量为

式中,显然0<ξi(k)≤1。
式(2)中rij反映了在某个观测时刻两个传感器观测值的接近程度;式(5)中ξi(k)反映了在某个观测时刻,第i个传感器的观测值和其他传感器(不包括第i个传感器本身)的观测值接近程度。
若只考虑某个观测时刻传感器观测值的一致性度量ξi(k),不考虑观测值在整个观测区间的可靠性,用表示k时刻对n个传感器观测值融合后对目标的估计,则可用一致性度量来计算。
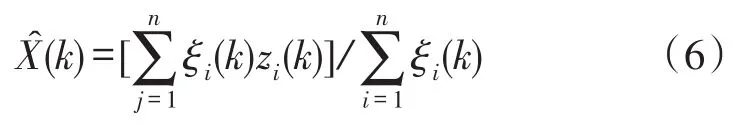
这种基于一致性度量对目标融合估计的方法,算法复杂度低,但并未挖掘和利用不同时刻的一致性度量所蕴含的传感器可靠性信息。
2 基于自适应加权估计的支持度融合算法
针对前述只考虑一致性度量的支持度融合算法存在的不足,有学者又提出一种新的考虑不同时刻的一致性度量所蕴含的传感器可靠性信息的融合算法。

k时刻,第i个传感器的观测一致性方差为

实际融合过程中,应当充分利用一致性均值大,且一致性方差小的传感器的观测信息。也就是说充分利用一致性和可靠性都很高的观测信息。所以,设计k时刻第i个传感器观测值的加权系数为:
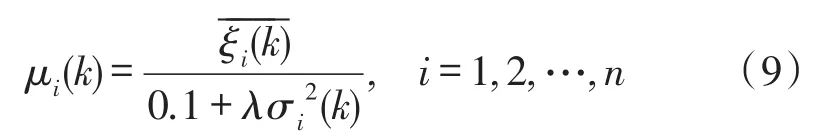

然而此种方法忽略了测量方差是由多种因素综合作用造成的,既包括传感器自身的可信度,也包括环境干扰等其他因素,因而导致估计值与真实值的偏差较大。
使用自适应加权算法改变各个传感器观测值方差对权系数的影响程度[10],既保证了传感器的可靠性,又能使融合后得到目标参数的总方差最小。而且自适应加权算法对各个传感器方差的计算不同于上述算法,考虑到环境因素等带来的噪声,与真实值更加接近。
2.1自适应加权算法
假定在N个传感器同时工作的状态下,将未知量X作为观测量,多传感器的其它观测量分别为:

第i个传感器的观测可表示为:

式(12)中ni(t)表示真实信号X(t)叠加的白噪声,ni(t)的方差用σi2=E[ni2(t)]表示,以E[·]表示数学期望。
如果对系统的观测是相互不干扰的,则对X的估计可以表示为:

式(13)中Wi为加权系数,并且
估计方差为:

要使式(14)中的总方差最小,构造辅助函数:

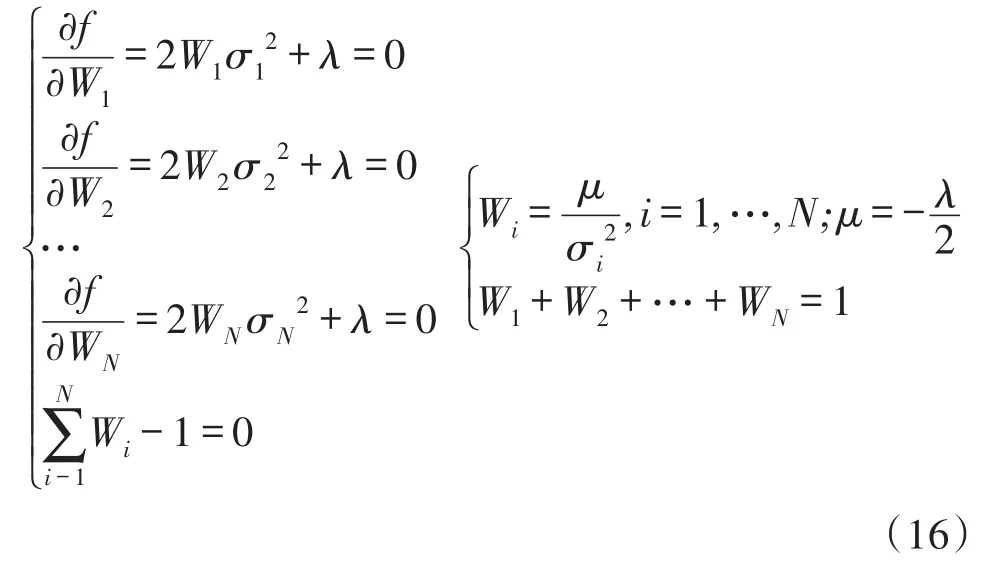
由式(16)可得:
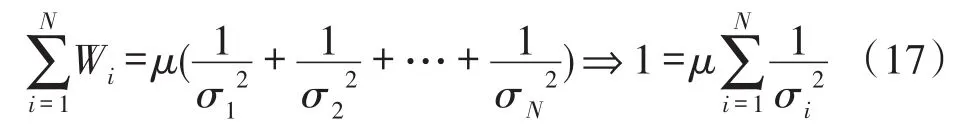
可得:


至此,我们便完成了使总方差最小的个传感器的权值分配。从式(19)我们可以看出来各个传感器的权值是和各自的方差有直接联系的。要求得这个权值Wj,我们只需要求出各传感器的方差σj即可。
接下来的工作是:如何根据各传感器的量测值确定他们的方差,并使求得的方差最接近真实值。
我们假设Xi,Xj是两个不同传感器i,j的测量值,那么有:

其中,X是真实值,ni,nj是各传感器的测量误差。由于ni,nj是白噪声,且和X不相关,则有:
美的以委托代销方式进行结算。在委托代销方式下,委托方在将货物移交给受托方时并不确认收入,而是等待受托方货物销售并开具代销清单,委托方收到代销清单的当天才确认收入。如果美的就2017年7月的销售业务与某公司签订委托代销合同,由该公司来销售这批商品,美的按销售额的一定比例支付佣金,该批货物于2017年8月1日移交给代销公司,美的在2018年1月1日收到代销公司开具的代销清单,金额300万元。在这种情况下,2017年7月签订委托代销合同,2017年8月1日发出货物,均不是美的的收入确认时间,所以美的在2017年度并不确认该批商品的相关收入,暂不针对该笔业务计算缴纳所得税。

下面是求解Rij,Rjj的过程:
首先我们用Rij(k),Rjj(k)来表示不同传感器测量值的样本k所对应的Rij,Rjj的估计值。
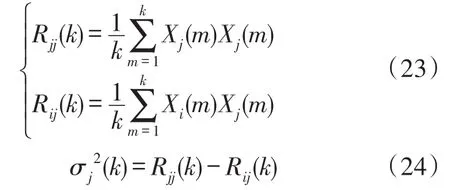
结合式(19)、式(23)、式(24)我们就可以计算出各个传感器的最佳权值。

2.2基于自适应加权估计的支持度融合算法
实际融合过程中,应当充分利用一致性均值大,且一致性方差小的传感器的观测信息。也就是说充分利用一致性和可靠性都很高的观测信息。基于支持度融合算法中权系数构造如下:
k时刻第j个传感器观测值的加权系数为:
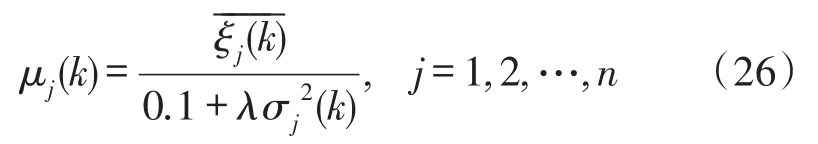
考虑到这种加权系数构造存在的不足,我们设计一种新的权系数构造方法:


3 实验分析
本实验采用六陀螺方案,将6个ADXRS300微机械振动陀螺焊接在同一电路板上,并对周围电路进行了设计。通过PXI4070 DMM板卡和PXI6502继电器板卡建立高精度测量系统,对同一轴向进行角速度测量。本实验中所用陀螺设定的带宽为40 Hz,为满足乃奎斯特定律,以200 Hz的频率进行陀螺输出数据的测量。为了验证算法的容错性,我们所使用的6个陀螺中,5个工作正常,其中一个测量误差较大。由于地球自转角速率很小,所以不作考虑。另外,参数t取1 000。
将虚拟陀螺系统置于温控转台内,并保持转台静止,按上述测量要求对六陀螺的输出进行测量,将测量数据上传至上位机进行数据的处理。原始数据如图1所示。
按照本文方法对6个陀螺的输出进行信息融合,根据2.2节推导的公式计算得到各个陀螺仪的融合权系数如图2所示。
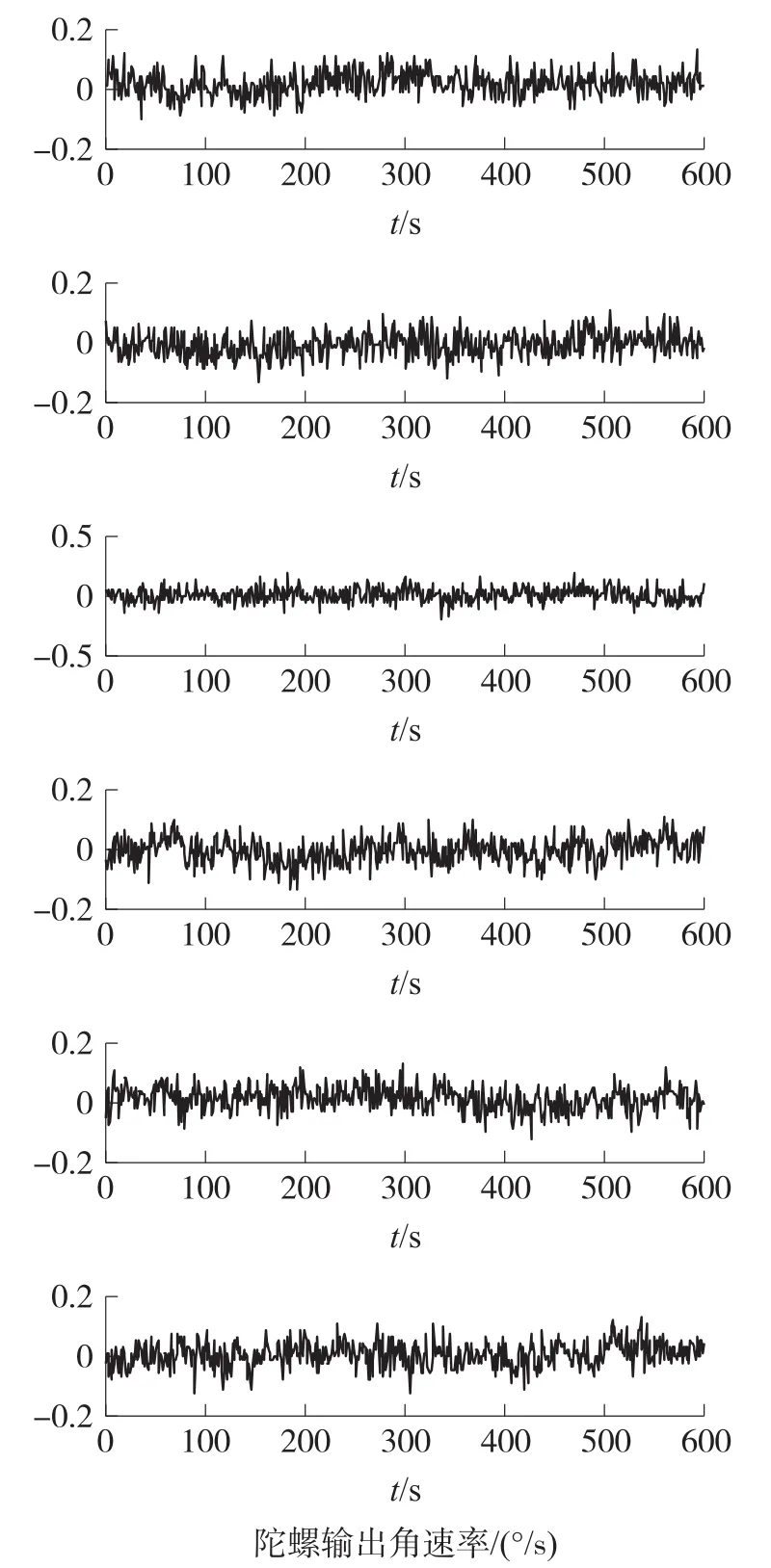
图1 静态条件下原始数据

图2 陀螺权系数图
从图2可以看出由于陀螺3的误差较大,所以融合权系数较小,和我们期望的结果相符。
利用本文方法进行融合的结果和基于平均值法和基于支持度法进行比较,结果如表1和图3所示。

表1 陀螺输出及信息融合结果统计表

图3 融合后的陀螺输出
从图3和表1中可以看出由于有1个陀螺的输出是不准确的,所以导致平均值法的融合效果明显差于其他两种方法,也就是容错性较差。而相比于基于支持度法,本文方法融合后的结果更接近真实值,且曲线变化幅度小,稳定性更好。
4 结束语
本文在基于支持度的融合算法的基础上,提出一种新的加权系数构造方法,这种方法利用自适应加权法的思想,改变各个传感器观测值方差对权系数的影响程度,既保证了阵列输出结果的可靠性,又能使融合后得到目标参数的总方差最小;利用这种方法对MEMS陀螺阵列输出数据进行信息融合,并与其他信息融合算法对比。实验结果表明,本文提出的权系数构造方法容错率更高,融合效果优于传统的平均值估计融合算法支持度融合算法。
[1]李士心,王晓亮,翁海娜,等.基于灰色模型和RBF神经网络的MEMS陀螺温度补偿[J].中国惯性技术学报,2010,18(6):742-746.Li Shixin,Wang Xiaoliang,Weng Haina,et al.Temperature Compensation of MEMS Gyroscope Based on Grey Model and RBF Neural Network[J].Journal of Chinese Inertial Technology,2010,18(6):742-746.
[2]Yang Bo,Wang Shourong,Li Hongsheng,et al.The Coupling Error Analysis of the Decoupled Silicon Micro-Gyroscope[C]//5th IEEE International Conference on Nano/Micro Engineered and Molecular Systems.Xiamen,China,2010:356-361.
[3]倪云舫,李宏生,杨波,等.硅微陀螺仪正交误差直流校正设计与分析[J].中国惯性技术学报,2014,22(1):104-108.Ni Yunfang,Li Hongsheng,Yang Bo,et al.Design and Analysis of a Quadrature Correction Method Using DC Voltages for Silicon Micro-Gyroscope[J].Journal of Chinese Inertial Technology,2014,22(1):104-108.
[4]邢晓辰,蔡远文,姚静波,等.基于改进自适应加权的多传感器融合监测[J].计算机测量与控制,2015,23(12):3988-3992.Xing Xiaochen,Cai Yuanwen,Yao Jingbo.Multi-Sensor Fusion Monitoring Based on Improved Adaptive Weighted Fusion Algorithm[J].Computer Measurement&Control,2015,23(12):3988-3992.
[5]Chang H L,Xue L,Qin W,et al.An Integrated MEMS Gyroscope Array with Higher Accuracy Output[J].Sensors,2008,8:2886-2899.
[6]邢晓辰,蔡远文,任江涛,等.一种考虑传感器精度的数据自适应加权融合算法[J].电讯技术,2015,55(10):1079-1083.Xing Xiaochen,Cai Yuanwen,Ren Jiangtao.An Adaptive Weighted Data Fusion Algorithm Considering Sensor Accuracy[J].Telecommunication Engineering,2015,55(10):1079-1083.
[7]李雪莲,孙尧,莫宏伟.基于最小二乘法的冗余信息数据融合算法实现[J].计算机工程与应用,2009,45(15):34-37.Li Xuelian,Sun Yao,Mo Hongwei.Research on Data Fusion Algorithm of Redundancy Information Based on Least Square Method[J].Computer Engineering and Application,2009,45(15):34-37.
[8]姜宇,金晶,张迎春,等.基于HHT的多MEMS陀螺信号融合算法研究[J].控制与决策,2012,27(5):646-651.Jiang Yu,Jin Jing,Zhang Yingchun,et al.Fusion Algorithm of Multi-MEMS Gyroscope Based on HHT[J].Control and Decision,2012,27(5):646-651.
[9]张华强,赵剡,陈雨.基于支持度的MEMS陀螺信息融合方法[J].宇航计测技术,2012,32(2):18-22.Zhang Huaqiang,Zhao Yan,Chen Yu.Information Fusion of MEMS-Gyro Based on Support Degree[J].Journal of Astronautic Metrology and Measurement,2012,32(2):18-22.
[10]李伟,何鹏举,高社生.多传感器加权信息融合算法研究[J].西北工业大学学报,2010,28(5):675-679.

孙田川(1993-),男,硕士,主要从事MEMS陀螺仪误差补偿技术研究,405528554@qq.com;

刘洁瑜(1970-),女,教授,博士学位,主要从事惯性导航技术。
Information Fusion Algorithm of MEMS-Gyro Based on Support Degree and Random Weighting
SUN TianChuan,LIU Jieyu*
(Department of Control Engineering,The Second Artillery Engineering University,Xi’an 710025,China)
The information fusion of MEMS-gyro can improve its measurement accuracy and reliability a lot.However,most traditional information fusion algorithms depend on prior knowledge of measuring information.This paper put forward a new construction method of weighting coefficient,which is on the foundation of the fusion algorithm based on support degree.The new method utilizes idea of adaptive weighting which can change the effects of the observation covariance matrix on weighting coefficients.Thus,the total variance of target parameter will be minimum and the reliability of gyroscope array can be guaranteed.Moreover,the new method also considers the environment noise,so the observation covariance approaches the true value closer.The result shows that the new method has a better effect.
MEMSgyroscope;fuzzyinformationgranulation;randomdrifts;intervalprediction;supportvectormachine
V241.5
A
1004-1699(2016)10-1548-05
2016-04-21修改日期:2016-06-06
- 传感技术学报的其它文章
- 基于HHT的脑电信号在不同阅读模式下的识别与分类*
- Development and Test of Software Method to Achieve Constant-Temperature-Difference Control for Thermal Wind Sensor*
- Analysis of the Effect of the Equivalent Parallel Resistor of theComb Capacitive Accelerometer*
- 基于球形内检测器的管道内磁场测量*
- 基于恒温谐波检测双回路瓦斯浓度仪研究*
- 炭黑/硅橡胶复合材料力敏元件热、力敏感试验研究*

