一次函数及其实际运用教学浅谈

林　艳

（雷波县西宁初级中学　四川凉山　616561）

一次函数及其实际运用教学浅谈

林艳

（雷波县西宁初级中学四川凉山616561）

函数是中学数学最重要的数学思想之一，是解决实际问题的一个有效的数学模型。将对一次函数的概念，图像，性质和一次函数在实际生活中的应用作一总结。

一次函数 概念 实际运用

一次函数是初中数学的一个重点，我们教学一次函数时，一定要把一次函数的定义、性质和性质紧密的结合起来。一次函数的定义、性质和图像是一次函数的三个重点，只要将三者紧密的结合起来，才能真正地领悟其真谛，掌握其要领，并能将有关问题运用到实际问题之中。所以这一部分从一次函数的概念、图像及其性质入手，通过经历观察、思考等数学活动，发展学生合情推理能力，使学生能有条理地、清晰地阐述观点，而且体验数形结合思想意义，逐步学习利用数形结合思想分析问题和解决问题，提高解决实际问题的能力并体会解决问题的策略多样性，发展实践能力和创新精神。

一、函数的概念及函数的表示方法

设在某变化过程中有两个变量x和y，如果对于x的每一个确定的值，y都有唯一确定的值与它对应，那么就说x是自变量，y是x的函数。

自变量的取值范围：当函数式可以用整式、分式、根式（或者是它们的组合式）表示时，必须使这些式子有意义，当函数式由实际问题构成时，还必须保证实际问题有意义。

二、一次函数的概念，图像和性质

1. 定义：形如bk xy+=（bk、是常数，k≠0）的函数，y叫做x的一次函数。

2.图像及性质：

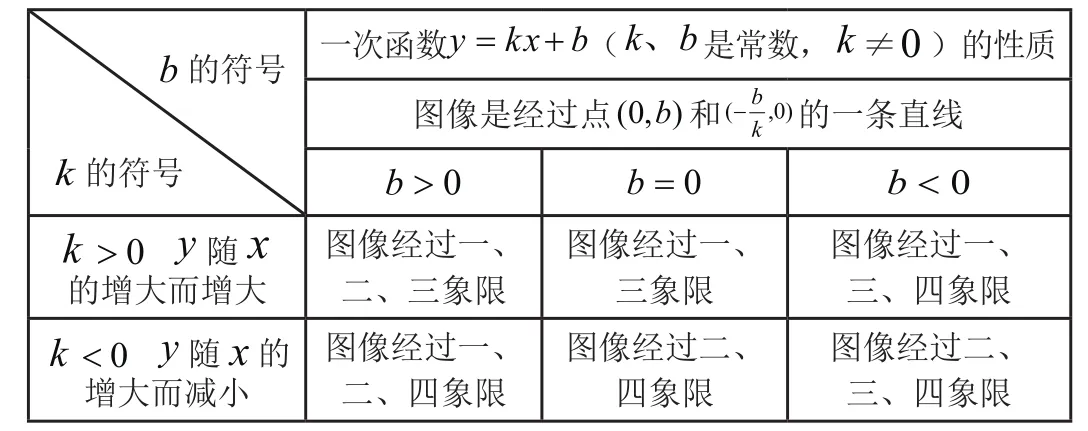
表1　一次函数的性质

三、一次函数的实际应用

在用一次函数的性质解决有关实际应用题的教学中，在学生已牢固掌握一次函数的图像及性质的基础上，引导学生怎样审题，弄清题意，建立一次函数模型，求出解析式，再根据解析式画出图像，弄清题目中要求的是什么量。一般情况都是已知x求y，或者是已知y求x的问题。要注意的几个点，直线与x轴的交点，与y轴的交点，或两个一次函数图像的交点。把一次函数几种类型的应用题叫学生多做，之后作一个归纳总结，使学生再掌握这几种典型题的基础上再加以灵活变通。

例如：甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度y（m）与挖掘时间x（h）之间的关系如图1所示，请根据图象所提供的信息解答下列问题：

（1）乙队开挖到30m时，用了 h.开挖6h时甲队比乙队多挖了 m；

（2）请你求出：①甲队在06x≤≤的时段内，y与x之间的函数关系式；②乙队在26x≤≤的时段内，y与x之间的函数关系式；

当x为何值时，甲、乙两队在施工过程中所挖河渠的长度相等？

解：

（1）2，10；

（2）设甲队在0≤x≤6的时段内y与x之间的函数关系式为y=1kx，由图可知，函数图象过点（6，60），

∴61k=60 解得1k=10 y=10x

设乙队在2≤x≤6的时段内y与x之间的函数关系为y=2kx+b，由图可知，函数图象过点（2，30）（6，50），∴

（3）由题意，得10x=5x+20，解得x=4（h）.∴当x为4h时，甲、乙两队所挖的河渠长度相等。

灵活应用一次函数知识解答实际问题是一次函数学习中基本的要求。解答这类问题时，要注意仔细审题，提取题目中的有用信息，根据实际问题中变量之间的关系，确定一次函数关系式，从而把实际问题转化为数学问题来解决。所以，在一次函数的教学中，采用概念----解析式----性质----应用为主线，结合数形结合思想，逐一突破，培养学生的逻辑思维能力和分析问题、解决问题的能力，形成知识上的系统与连续。

在新课程理念的指导下，我们的一切教学都要围绕学生的成长与发展做文章，真正让学生理解、掌握真实的知识和真正的知识。要实现此目的 ：首先，要设计适合学生探究的素材。教材对一次函数的性质是从增减来描述的，我们认为这种对性质的表述是教条化的，对这种学术、文本状态的知识，学生不容易接受。当然教材强调所呈现内容的逻辑性、严密性与科学性是合理的。但是能让学生理解和接受的知识才是最好的。如果牵强的引出来，不一定是好事。其次，探究教学的过程就是实现学术形态的知识转化为教育形态知识的过程。只有这样探究才是有价值的，真知才会有生长性。要表现过程的真实与自然，从建构主义的观点出发，就是要尊重学生各自的经验与思维方式、习惯。结论是一致的，但过程可以是多元的，教师要善于恰倒好处地优化提炼学生的结论。