基于压缩感知的非线性OFDM系统迭代信道估计算法

戈立军，程以泰，张　华，王　松，陶　进

(天津工业大学 电子与信息工程学院，天津 300387)



基于压缩感知的非线性OFDM系统迭代信道估计算法

戈立军，程以泰，张华，王松，陶进

(天津工业大学 电子与信息工程学院，天津 300387)

针对因非线性失真引起的正交频分复用(orthogonal frequency division multiplexing，OFDM)系统信道估计性能下降的问题，提出了一种基于压缩感知的非线性OFDM系统迭代信道估计算法。在算法实现过程中，利用信道与非线性噪声的双重稀疏性，将导频信息作为观测矩阵进行压缩感知信道估计，再将所得信道信息看作观测矩阵进行压缩感知非线性失真估计，进而对信号进行非线性补偿，并逐步循环迭代至算法收敛。仿真表明，在稀疏信道下，该算法在较少的迭代次数下即可有效减小非线性失真对信道估计的影响，且比现有方法性能更优，仿真证明了该方法在性能上的优越性。

正交频分复用(OFDM)；非线性失真；压缩感知；信道估计

0　引　言

正交频分复用(orthogonal frequency division multiplexing，OFDM)具有频带利用率高、抗符号串扰能力强、抗频率选择性衰落能力强等优点，是高速无线通信领域的核心。信道估计是OFDM系统的关键技术之一，其精度直接影响衰落信道下的系统性能。目前已有大量关于OFDM信道估计算法的研究，然而现有方法几乎均未考虑OFDM信号非线性失真的影响[1-4]。在OFDM系统中，高峰均比信号经过功率放大器会产生非线性失真(nonlinear distortion，NLD)，而基于带有NLD的信息进行信道估计，其性能将急剧下降。现有的性能较好的降低峰均比算法多数具有较高的复杂度[5-7]，而实施简单的限幅法仍会使系统中存在NLD[8]。

近年来，已有少量学者开始研究非线性OFDM系统的信道估计问题[9-11]。文献[9]最早提出一种迭代估计算法，基于线性最小均方误差(linear mini-mum mean square error，LMMSE)估计信道，基于压缩感知估计NLD噪声。文献[10-11]提出最小二乘法(least square，LS)结合判决反馈的联合迭代算法，该方法需在接收端对信号进行快速傅利叶逆变换(inverse fast Fourier transform，IFFT)重构。上述联合估计算法均未考虑信道在很多场景下所具有的稀疏特性。若信道较为稀疏，且导频数量小于信道长度，则LS，LMMSE的信道估计性能将大大降低[1-2]。而目前国内外尚未有关于考虑非线性失真影响下的稀疏信道估计算法的研究。

本文针对存在非线性失真影响下的OFDM稀疏信道估计问题，利用信道与NLD噪声的双重稀疏性，提出一种基于压缩感知的非线性OFDM系统迭代信道估计算法，分别将导频和估计出的信道信息看作观测矩阵，同时利用压缩感知对信道和NLD进行估计，实现了非线性OFDM系统的高性能信道估计，并获得比现有联合估计方法更优的性能。

1　非线性OFDM系统模型

在OFDM系统中，频域信号X=[X0,X1,…,XN-1]T通过N个相互正交的子载波进行传输，其中第k个子载波上的数据Xk为相移键控(phase shift keying，PSK)，正交振幅调制(quadrature amplitude modulation,QAM)等数字映射的结果，则经过离散傅里叶逆变换(inverse discrete Fourier transform，IDFT)调制的时域信号可表示为

(1)

定义向量x=[x0,x1, …,xN-1]T，则(1)式可表示为矩阵形式

x=QX

(2)

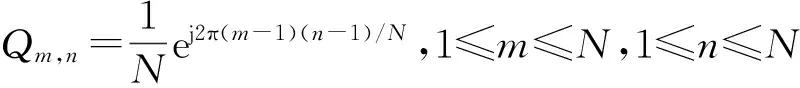
信号经过功率放大器时，由于其线性度的限制产生NLD，引入NLD的信号可表示为[12]

(3)

(3)式中，β表示增益。定义向量d=[d0,d1, …,dN-1]为引入的NLD，其可看作稀疏的加性噪声。为分析方便，令β为1，则引入NLD的信号可表示为

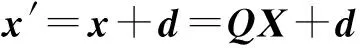
(4)

为使放大器工作于线性区域，在发送端对信号进行限幅处理，则经过限幅的时域信号可表示为

(5)

(5)式中，A为归一化限幅门限。为表征限幅法对信号的影响程度，定义限幅后的峰均抑制比为10lg[A2/E(|xn|2)]，则限幅门限值越大，峰均抑制比越大，系统产生的NLD影响越小，NLD噪声的稀疏度越高。

受多径信道影响，接收信号可表示为

(6)

(6)式中：⊗表示循环卷积运算；z=[z0,z1, …,zN-1]T表示加性高斯白噪声；h=[h0,h1,…,hL-1,01×(N-L+1)]T，其中任一hl,l=0,1,…,L-1为信道冲击响应(channel impulse response，CIR)。

经过离散傅里叶变换(discrete Fourier transform，DFT)解调所得频域信号可表示为

(7)

定义向量Y=[Y0,Y1, …,YN-1]T，则将(7)式写为矩阵形式

Y=QHy=HX+HD+Z

(8)

(8)式中：QΗ为N×N维傅里叶变换矩阵；H=diag(H0,H1, …,HN-1)为信道频域响应构成的对角矩阵；D=QΗd为NLD的N×1维频域形式；Z=QΗz为高斯白噪声的频域形式。(8)式即为同时存在多径信道与NLD影响时的OFDM解调信号模型。

2　压缩感知基本原理

压缩感知是一种针对稀疏信号的信号压缩理论。设x=[x1,x2,…,xN]T,xi∈RN为N×1维信号，它可以通过一组正交基Ψ进行映射，即

(9)

(9)式中，a为x在Ψ域的表示。如果a中只有K(K≪N)个非零值，则称x在Ψ域是可压缩的。对信号x进行观测

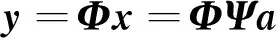
(10)

(10)式中：y=[y1,y2,…,yM]T为M×1维观测值；Φ为M×N维观测矩阵。压缩感知理论证明，如果观测矩阵Φ满足严格等距条件[13]，则可以从M个观测值中以很大的概率重建稀疏度为K的原始信号x，其中

M≥cKlb(N/K)≪N

(11)

(11)式中，c为一较小的常数[14]。

经典信号重构算法通过求解如下最优化问题，从少量观测信号中恢复信号x。

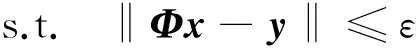
(12)

(12)式中，ε为一个极小的噪声值。求解(12)式有两类方法：一类是基于凸优化的方法，如基追踪(basis pursuit，BP)算法。该类方法重构精度高，但运算复杂，不便于实现；另一类是基于贪婪迭代的方法，如匹配追踪(matching pursuit，MP)算法、正交匹配追踪算法(orthogonal matching pursuit，OMP)[15]。贪婪类算法重构精度不如凸优化类算法，但运算简单，实现方便。

3　压缩感知迭代信道估计算法

大量研究表明，在不考虑NLD影响的线性OFDM系统中，利用压缩感知理论可获得比传统方法更优的稀疏信道估计性能[3-4]。其核心原理如下。

略去非线性系统模型中的非线性失真项，则(8)式可改写为

(13)

(13)式中，X′=diag(X0,X1, …,XN-1)为发送端频域数据所构成的对角矩阵。选取导频所在的行，则(13)式可进一步改写为

(14)

本文在前人研究基础上，引入NLD对OFDM系统的影响，提出基于压缩感知的非线性OFDM系统迭代信道估计算法。图1为基于该迭代算法的非线性OFDM系统原理框图。发送端加入限幅器，则系统在不同限幅门限下产生不同的非线性失真噪声。非线性OFDM信号经过稀疏信道到达接收端。接收端FFT变换后的信号如(8)式所示，从中提取导频并基于导频实施迭代估计算法。算法的具体过程如图1所示，其中，n(t)表示加性高斯白噪声。

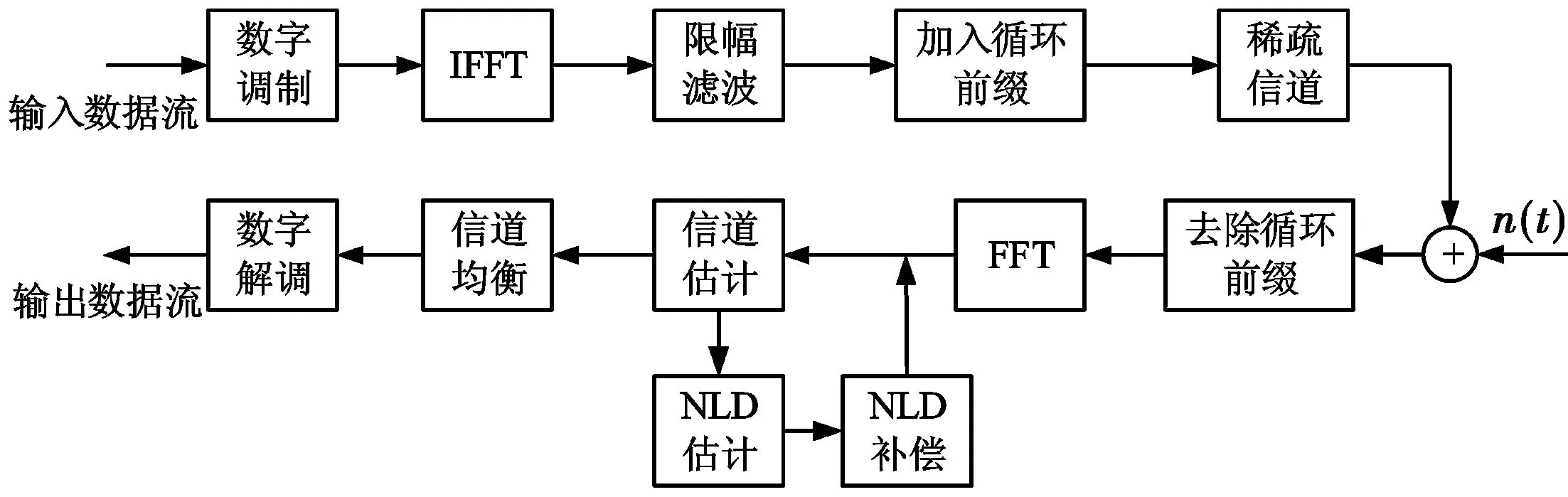
图1　非线性OFDM系统迭代信道估计原理框图Fig.1　Logic diagram of iterative channel estimation in nonlinear OFDM system

1)初估计。对非线性信号模型(8)式进行变形，将向量X改写为对角矩阵形式，并选取导频所在的行，可得

(15)

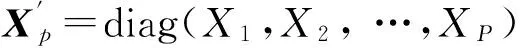
初始化时，令i=0，并将此时的非线性失真看作噪声，从而归并到噪声项中，则(15)式可写为

(16)

(17)

至此，算法完成了信道的初估计。初估计时由于忽略了NLD噪声的影响，其估计结果即可表示传统压缩感知信道估计在非线性OFDM系统中的性能。

2)迭代估计。对估计出的hi进行傅里叶变换，得到其频域响应Hi。将Hi代入(8)式并选取导频行，可得

(18)

(18)式中，VP为P×1维列向量。

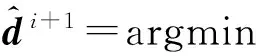
(19)

将求得的di+1代入(15)式对信号进行非线性失真补偿，可得

(20)

(20)式中，UP为P×1维列向量。

再利用OMP算法对(20)式中的hi+1进行求解，得

(21)

至此，算法完成了第1次迭代运算。循环重复(18)-(21)式的过程，可进行多次迭代运算，从而提高信道估计精度。利用迭代估计出的信道响应即可对已进行非线性失真补偿的信号实施信道均衡。

4　仿真分析

为仿真算法性能，构建的OFDM仿真系统中共有512个子载波，其中包括336个信息子载波，80个导频子载波，96个空子载波，循环前缀长度为128，64QAM，5/8低密度奇偶校验码(low density parity check code，LDPC)编码。建立稀疏多径信道模型，信道长度为90，其中有效路径数为12。在该仿真环境下，对本文提出的迭代方法与文献[9-10]方法的性能进行仿真比较。为了更好地对比方法性能，文献[9]中采用OMP算法利用压缩感知来估计非线性失真。

限幅门限为4 dB时，不同方法在不同信噪比(signal noise ratio,SNR)下的信道估计均方误差曲线(mean square error，MSE)如图2所示。可以看出，随着信噪比的增加，各方法的估计精度越来越高。当信噪比较低时，本文算法迭代次数影响不明显，这是由于压缩感知OMP算法抗噪声性能较差所致；而当信噪比较高时(≥17 dB)，随着迭代次数的增加，信道估计精度明显优于不迭代的初估计，说明了考虑非线性失真对信道估计影响的必要性及本文算法对于改善非线性系统信道估计性能的优越性。本文算法与文献算法在均迭代3次的情况下，与假设不考虑NLD的理想信道估计性能曲线相比，本文算法性能最为接近。由于信道为稀疏信道，且信道长度大于导频数量，LS与LMMSE的信道估计性能较差。同时，由于子载波数不为导频数的整数倍，LS性能劣于LMMSE。

限幅门限为4 dB时，不同方法在不同信噪比下的系统误比特率(bit error ratio，BER)曲线如图3所示。可以看出，非线性系统的信道估计性能均与理想线性系统有一定差距，但本文算法性能最为接近理想情况。且随着迭代次数的增加，算法性能明显好于不迭代的初估计。在信噪比为30 dB时，初估计的BER为1×10-3，迭代3次的BER为1×10-4。

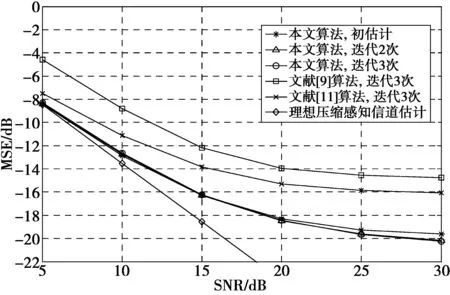
图2　限幅门限4 dB下不同方法的信道估计均方误差Fig.2　MSE of channel estimation with different methods in 4 dB clipping threshold conditions

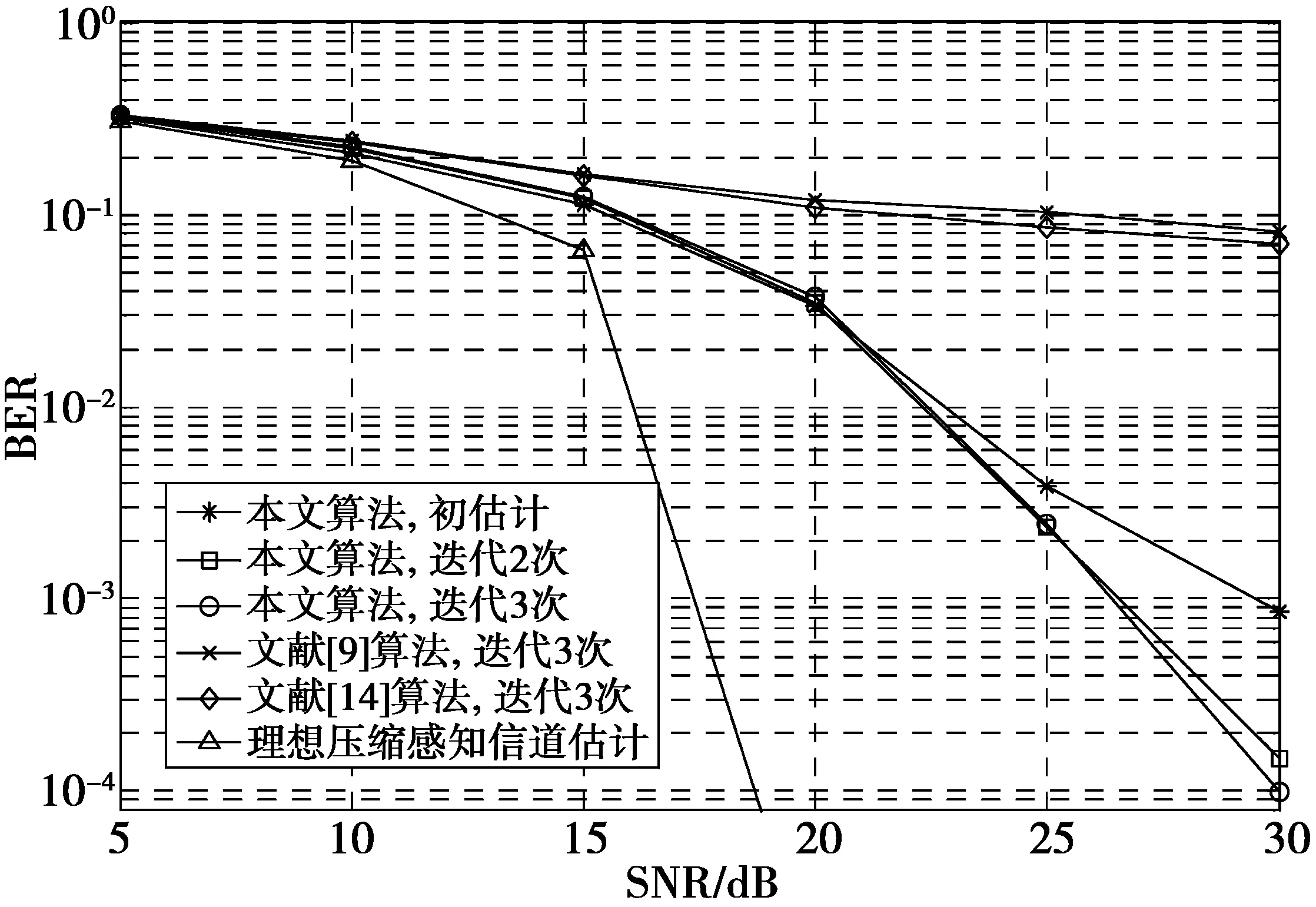
图3　限幅门限4 dB下不同方法的系统误比特率Fig.3　BER of system with different methods in 4 dB clipping threshold conditions

信噪比为30 dB时，不同方法在不同限幅门限下的信道估计MSE曲线如图4所示。可以看出，随着限幅门限的升高，各方法的信道估计性能越来越好。这是由于门限值变大，非线性噪声减小，对信道估计的影响减小，且非线性噪声的稀疏度增大，对于采用压缩感知的方法而言，其性能逐渐提高。在相同的限幅门限下，本文算法进行初估计、2次迭代及3次迭代的性能逐渐提高。3次迭代对应的3种方法中，本文算法性能最优。

信噪比为30 dB时，不同方法在不同限幅门限下的系统BER曲线如图5所示。可以看出，随着门限值的升高，不同方法对应的系统性能逐渐提高，且各种方法之间的性能具有同样的结论。在门限值为4 dB时，本文算法进行初估计、2次迭代、3次迭代的误比特率分别为1×10-3，2×10-4，1×10-4，且均明显优于文献算法。

图4　信噪比30 dB不同门限下的信道估计均方误差Fig.4　MSE of channel estimation with different methods in different clipping threshold conditions when SNR is 30 dB

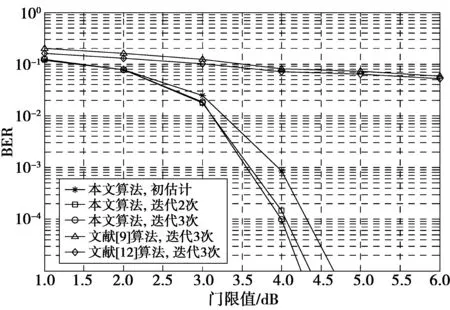
图5　信噪比30 dB不同门限下的系统误比特率 Fig.5　BER of system with different methods in different clipping threshold conditions when SNR is 30 dB

5　结　论

本文针对非线性OFDM系统的信道估计问题，提出了基于压缩感知的迭代信道估计方法。利用压缩感知估计信道与非线性失真，并循环迭代。仿真表明，在稀疏信道下，该方法可有效提高非线性OFDM系统的信道估计精度，且具有比现有方法更好的性能。

[1]张伟, 陈前斌, 张天骐, 等. 基于傅立叶变换的OFDM信道估计方法研究[J]. 重庆邮电大学学报：自然科学版, 2007, 19(4): 472-476.

ZHANG Wei, CHEN Qianbin, ZHANG Tianqi, et al.DFT based channel estimation methods for OFDM[J]. Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition,2007,19(4):472-476.

[2]GENG Nian,YUAN Xiaojun,LI Ping. Dual-diagonal LMMSE channel estimation for OFDM systems[J].IEEE Transactions on Signal Processing,2012,60(9):4734-4746.

[3]何维, 唐彦楠, 陈美铃. MIMO-OFDM中稀疏度自适应的信道估计方法[J]. 重庆邮电大学学报：自然科学版, 2015, 27(6): 711-716.

HE Wei, TANG Yannan, CHEN Meiling. Channel estimation method of adaptive sparsity for MIMO-OFDM[J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition,2015,27(6):711-716.

[4]田玮, 张玉, 王红军, 等. 基于自适应步长的MIMO-OFDM信道估计技术[J].重庆邮电大学学报：自然科学版, 2013, 25(5): 579-582.

TIAN Wei, ZHANG Yu, WANG Hongjun, et al. Channel estimation technology for MIMO-OFDM based on adaptive step-size[J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2013, 25(5): 579-582.

[5]RODRIGUES M R D, WASSELL L J. IMD reduction with SLM and PTS to improve the error-probability performance of nonlinearly distorted OFDM signals[J].IEEE Transactions on Vehicular Technology,2006, 55(2): 537-548.

[6]李英善, 段燕辉, 王猛, 等. 一种降低OFDM系统峰均比的循环反馈SLM方法[J].重庆邮电大学学报：自然科学版, 2014, 26(1): 49-53.LI Yingshan,DUAN Yanhui,WANG Meng,et al.A new SLM method with feedback searching for OFDM system[J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition,2014,26(1):49-53.

[7]MOHAMMADY S,SIDEK R M, VARAHRAM P,et al.A low complexity selected mapping scheme for peak to average power ratio reduction with digital predistortion in OFDM systems[J].International Journal of Communication Systems, 2013, 26(4): 481-494.

[8]WANG Jianping, YAN Jing, HE Zhen. SLM and clipping joint algorithm for PAPR reduction in OFDM system[J].Journal of Information and Computational Science, 2015, 12(1): 143-152.

[9]MOHAMMADNIA A M, GHASSEMI A, LAMPE L.Compressive sensing recovery of nonlinearly distorted OFDM signals[C]//IEEE.2011 IEEE International Conference on Communications,Kyoto, Japan,IEEE International Conference on Communications.New York：IEEE Press，2011:1-5.

[10] 解永生, 覃荣华, 周磊磊, 等. 多媒体传感网中限幅OFDM的信道估计算法[J]. 华中科技大学学报：自然科学版, 2012, 40(8): 123-128.

XIE Yongsheng,QIN Ronghua,ZHOU Leilei, et al.Channel estimation algorithm of clipping OFDM in wireless multimedia sensor networks[J]. Journal of Huazhong University of Science and Technology：Natural Science Edition, 2012, 40(8): 123-128.

[11] XIE Yongsheng, ZHOU Leilei, FU Yaoxian. A novel channel estimation method for clipped OFDM systems based on virtual pilots[J]. Journal of Computational Information Systems, 2012, 8(5): 1905-1912.

[12] STERBA J,GAZDA J,DEUMAL J,et al. Iterative Algorithm for Channel Re-Estimation and Data Recovery in Nonlinearly Distorted OFDM Systems[J].Acta Polytechnica Hungarica，2010, 7(1): 103-118.

[13] CANDES E J.The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9): 589-592.

[14] LI B, PETROPULU A. RIP analysis of the measurement matrix for compressive sensing-based MIMO radars[C]//IEEE.2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop，A Coruna, Spain: Proceedings of the IEEE Sensor Array and Multichannel Signal Processing Workshop.New York:IEEE Press,2014:497-500.

[15] GUI G,MEHBODNIYA A,WAN Q,et al.Sparse signal recovery with OMP algorithm using sensing measurement matrix[J].IEICE Electronics Express,2011,8(5):285-290.

戈立军(1984-)，男，天津人，副教授，博士，主要研究方向为OFDM无线通信技术。E-mail: gelj@mail.nankai.edu.cn。

程以泰(1993-)，男，河南信阳人，硕士研究生，主要研究方向为OFDM系统非线性失真与信道估计技术。E-mail: 1037312341@qq.com。

张华(1991-)，男，安徽安庆人，硕士研究生，主要研究方向为OFDM系统压缩采样技术。E-mail: 991926659@qq.com。

王松(1992-)，男，内蒙古呼伦贝尔人，硕士研究生，主要研究方向为OFDM系统sigma-delta调制技术。E-mail: 1219107403@qq.com。

陶进(1991-)，女，安徽安庆人，硕士研究生，主要研究方向为OFDM可见光系统应用技术。E-mail: 790439519@qq.com。

(编辑：王敏琦)

s：The National Natural Science Foundation of China(61302062)；The Research Program of Application Foundation and Advanced Technology of Tianjin for Young Scientist(13JCQNJC00900)；The Open Funds of Tianjin Key Laboratory for Civil Aircraft Airworthiness and Maintenance(1040030205)

Iterative channel estimation based on compressed sensing for nonlinearly distorted OFDM systems

GE Lijun, CHENG Yitai, ZHANG Hua, WANG Song, TAO Jin

(School of Electronics and Information Engineering, Tianjin Polytechnic University, Tianjin 300387, P.R.China)

An iterative channel estimation algorithm based on compressed sensing is proposed to improve the performance of channel estimation in orthogonal frequency division multiplexing(OFDM) systems caused by nonlinearly distortion. By using the dual-sparsity of channel and nonlinear distortion, compressed sensing based channel estimation is firstly implemented by considering the pilots as the observation matrix, and compressed sensing based nonlinear distortion estimation is then implemented by considering the estimated channel information as the observation matrix. After compensating the nonlinear distortion of the signal, the whole process repeats for iterative operation. Simulation shows that the proposed algorithm can effectively reduce the impact of nonlinear distortion on channel estimation and it has a better performance than the existing methods in sparse channels. It demonstrates that this algorithm has superior performance.

orthogonal frequency division multiplexing(OFDM); nonlinear distortion; compressed sensing; channel estimation

10.3979/j.issn.1673-825X.2016.05.011

2016-03-18

2016-09-13通讯作者：程以泰1037312341@qq.com

国家自然科学基金(61302062)；天津市应用基础及前沿技术研究计划青年基金(13JCQNJC00900)；天津市民用航空器适航与维修重点实验室开放基金(1040030205)

TN914.4

A

1673-825X(2016)05-0680-06