基于用户集合势估计的认知无线电合作频谱感知

申　滨，高　凯，黄晓舸，陈前斌

(重庆邮电大学 移动通信技术重点实验室，重庆 400065)



基于用户集合势估计的认知无线电合作频谱感知

申滨，高凯，黄晓舸，陈前斌

(重庆邮电大学 移动通信技术重点实验室，重庆 400065)

频谱感知技术是认知无线电系统的基本功能，是实现已授权频段的次级动态接入和共享的前提。提出基于用户集合势估计的合作频谱感知方案，旨在通过GEEF(gerschgorin exponentially embedded families)，SPEEF(sampled power exponentially embedded families)等算法估计出用户的集合势，即适合参与合作频谱感知的最优用户个数，再从全部合作用户中筛选出相应的频谱观测数据生成全局检测统计量，通过与判决门限进行对比，最终对授权用户状态做出判决。理论分析与实验结果表明，提出的方案能够有效地提高频谱感知的性能。

认知无线电；合作频谱感知；用户集合势估计；用户选择

0　引　言

认知无线电[1](cognitive radio, CR)致力于解决传统固定频谱分配方式频谱资源短缺和频谱浪费的问题，能够实现次级用户(secondary user, SU)在已授权频段(licensed frequency bands, LFB)上的机会性低优先级动态接入。频谱感知技术作为认知无线电的基本前提受到广泛研究，其目的在于准确、快速地对LFB的实时占用状态做出判决，以便于SU在尽可能少地对授权用户(primary user, PU)产生干扰和影响的情况下伺机接入授权频段。

早期经典的单用户频谱感知方案包括：匹配滤波器检测方案、循环平稳检测方案、能量检测方案(energy detection, ED)等[2]。匹配滤波器检测和循环平稳检测在不同程度上需预知PU信号结构和信道信息等先验知识，在实际情况中难以满足。ED方案由于仅需预知噪声功率而得到广泛研究。然而，基于ED的单用户频谱感知方案容易受周围环境因素(噪声功率不确定度、隐终端效应等)的影响，因而具有较大的感知性能缺陷和应用局限性。

近年来，多用户合作频谱感知方案因相对于单用户频谱感知方案的性能优势而受到广泛关注。合作频谱感知广泛采用数据软融合(soft data fusion, SDF)方案，融合中心(fusion center, FC)收集各个合作用户发送过来的感知数据生成全局检测统计量(global test statistics, GTS)并完成最终判决。

文献[3]提出了基于随机矩阵理论(random matrix theory, RMT)的最大最小特征值(maximum minimum eigenvalue, MME)感知方案以及能量最小特征值(energy minimum eigenvalue, EME)感知方案。其中，MME方案利用接收信号协方差矩阵的最大特征值与最小特征值的比值生成GTS；EME方案则利用接收信号的平均能量与协方差矩阵最小特征值的比值生成GTS，2种方案均不需要任何先验信息，克服了噪声不确定度的问题。然而，MME方案与EME方案检测相关信号时，性能不足；检测独立同分布信号(independent identically distributed signal, IIDS)时，性能不及ED方案。实际上，在检测IIDS时，ED方案仍是性能最优的方案[4]。文献[5]提出了最大特征值检测(maximum eigenvalue detection, MED)方案，在预知噪声功率并检测相关信号时，性能优于ED。文献[6]阐述了信号子空间特征值(signal-subspace eigenvalue, SSE)检测算法和算术几何平均(arithmetic to geometric mean, AGM)检测算法。AGM方案无需任何先验信息，当噪声不确定度存在时，检测性能优于ED；SSE方案需要预知噪声功率，仅当检测相关信号时，检测性能优于ED方案。文献[7]提出最大最小差(difference of maximum and minimum, DMM)检测方案，利用协方差矩阵最大特征值和最小特征值之差生成GTS检测相关信号时，检测性能优于ED。文献[8]提出基于DMM改进的平均特征值差(difference of means of eigenvalues, DME)检测方案，计算感知环境中M个SU的协方差矩阵特征值，利用其中K个较大特征值平均值与M-K个较小特征值的平均值之差生成GTS。文献[9]提出理想情况下的最优能量合并检测(optimally combined energy detection, OCED)方案和实际情况下的盲能量合并检测(blindly combined energy detection, BCED)方案。OCED方案利用发射信号协方差矩阵的最大特征向量与接收信号矩阵合并生成GTS，检测相关信号时检测性能大幅优于ED方案，但需要预知信号协方差矩阵，这在实际中难以获得。BCED方案将协方差矩阵的最大特征向量与采样矩阵合并生成GTS，不需要任何先验信息，检测相关信号时检测性能优于ED方案。

1　系统模型

PU信号是否存在可采用二元假设表示。假设认知无线电网络中共有M个用户参与合作感知，其中第i个SU接收机在每次频谱感知时间内进行N次采样得

(1)

在假设H1下，M个SU的接收信号协方差矩阵为

(2)

(3)

(4)

(5)

(6)

合作频谱感知主要依靠FC完成GTS的生成。文献[14]提出一种等增益合并(equal gain combining, EGC)算法，等效于多用户ED方案，其GTS为

(7)

文献[14]提出理想无限次采样下的OCED方案和实际有限次采样下的BCED方案，前者需要预知信号协方差矩阵，在实际环境中难以获得，后者则无需预知任何先验信息，其GTS分别为

(8)

(9)

2　基于用户集合势的合作感知

2.1用户集合势估计算法

考虑实际感知环境中，每个SU的信道条件各异，一般地，协方差矩阵Rs的前K个特征值远大于后M-K个特征值，即λ1≥λ2≥…≥λK≥λK+1≥…≥λM,因此，在这个意义下，参与合作感知的M个用户可以分为信道条件较好的集合和信道条件恶劣的2个集合。考虑先估计出信道条件较好的合作感知用户集合中的用户个数K，即用户集合势，然后再筛选出前K个较大特征值对应的特征向量参与合作感知，生成最终的GTS。

下面介绍用于估计用户集合势K的算法，包括AIC，MDL，EEF，GEEF，SPEEF。

首先，考虑采用基于信息论准则(information theory criterion, ITC)的Akaike信息准则(Akaike information criterion, AIC)和最小描述长度准则(minimum description length, MDL)来估计用户集合势，其表达式为[15]

2K(2M-K)

(10)

K(2M-K)logN

(11)

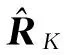
(12)

然而，AIC和MDL存在一定的问题。AIC 估计并不满足一致性，MDL 受SNR影响较大，难以满足低SNR下的集合势估计的性能要求。EEF准则在模型阶次估计和稳定性方面具有良好的性能[16]，自然地成为可选的一种方案。

具体地，考虑利用EEF准则，进一步提高估计性能，其函数表达式为

(13)

(13)式中：u(·)表示单位阶跃函数；φK为EEF对应的自适应参数个数；LK(y)表示似然比函数，其定义为

(14)

(15)

(16)

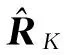
(17)

(17)式中

(18)

在用户集合势估计的范畴下，将GEEF的表达式改写为

(19)

(19)式中

(20)

(21)

(21)式中

(22)

(23)

图1所示为当SU总数为M=12，信道条件较好的用户个数为K=6，采样次数N=1 000与N=5 000时，各个算法估计用户集合势的性能仿真。由图1可以看出，相对于AIC，MDL算法，EEF，GAIC[17](gerschgorin akaike information criterion)，GEEF，SPEEF算法对于采样次数和信噪比具有更低的依赖程度。当采样次数和信噪比增加到一定大时，AIC，MDL算法也可达到较高性能水平，但仍然劣于其他算法。因此，重点考虑EEF，GAIC，GEEF，SPEEF算法在用户集合势估计时的应用。设置多组M，K，N的参数可得出用户集合势估计算法的估计性能对比，如表1所示。

2.2用户选择

(24)

由(24)式可得理想条件下的用户选择向量μ的第i个选择元素为

(25)

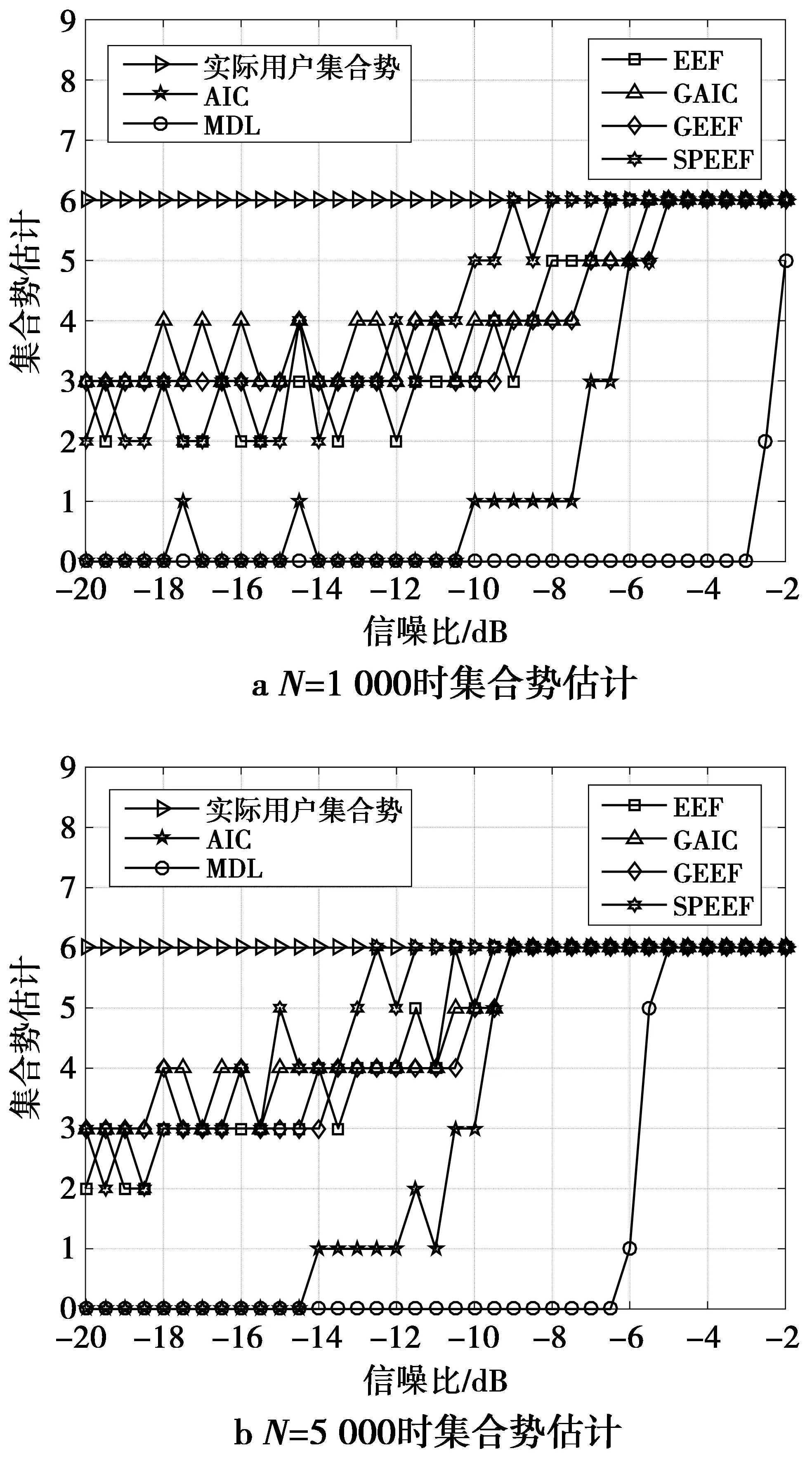
图1　各个算法用户集合势估计性能Fig.1　Simulation of different algorithms estimating user set cardinality

类别ITC盖氏圆盘ITCEEF系列AICMDLGAICGMDL[17]EEFGEEFSPEEF估计性能分析SNR足够大(约-5dB),N=1000,有较好的估计能力;SNR较小时,低估严重。SNR大(约-2dB),但受N影响大。在N较大时才具有估计能力;SNR较小时,不具备估计能力。SNR较大(约-6dB),N=1000,可使估计性能较好;SNR较小时,具备估计能力,但会低估。SNR大(约-3dB),N=1000,能够较好估计;SNR较小时,即使N很大也会严重低估。SNR较大(约-7dB),N=1000,估计性能良好;SNR较小时,即使N很大也会低估。SNR较大(约-5dB),较小的N即可具备良好的估计能力;SNR较小时,提高N的数目可提高估计能力,但易受M个数影响。SNR较小(约-9dB),N=1000,估计能力优秀,且不易受影响;SNR很小时,N足够大,估计能力可观。一致性非一致估计非一致估计非一致估计一致估计一致估计非一致估计一致估计

2.3合作感知

利用筛选出的特征向量进行合并，分别生成最优用户集合势估计方案(optimalusersetcardinalityestimation,OUSCE)和盲用户集合势估计方案(blindusersetcardinalityestimation,BUSCE)的GTS分别为

(26)

(27)

图2　用户集合势估计感知算法流程图Fig.2　Flow chart of USCE based sensing algorithm

3　仿真结果及分析

在Matlab环境下进行5 000次迭代的MonteCarlo仿真，设定M=12，K=6，期望的虚警概率设置为10%。根据 (26) 式和(27) 式中算法实现条件的不同，对基于EEF，GAIC[9]，GEEF，SPEEF的USCE合作算法的性能评估分为2类，即理想条件下预知信号协方差矩阵的OUSCE类以及实际条件下未知先验信息的BUSCE类。算法性能以检测概率和虚警概率指标来衡量。

仿真1取采样次数N为1 000，仿真信噪比范围为[-18dB,-4dB]，图3a和图3b分别反映了OUSCE算法及其他算法在不同信噪比时的检测概率和虚警概率的变化曲线。由图3a可以看出基于EEF，GAIC，GEEF，SPEEF的OUSCE合作算法在低信噪比时有较高的检测概率，相对于传统的OCED算法检测性能有所提升。而SPEEF算法以较低的算法复杂度便获得了与EEF，GEEF，GAIC算法相近的感知性能。图3c和图3d反映的是BUSCE算法及其他算法的检测概率和虚警概率。由图3c可以看出基于EEF，GAIC，GEEF，SPEEF的BUSCE算法相对于原始BCED算法的检测性能有明显提升，在不需要任何先验信息的条件下检测性能接近需要预知噪声功率的EGC方案。

仿真2图4a和4b所示为信噪比设置为-10dB时OUSCE合并方式下，各算法检测概率和虚警概率随采样次数N变化的曲线，图4c和4d所示为信噪比设置为-10dB时BUSCE合并方式下，各算法检测概率和虚警概率随采样次数N变化的曲线。由图4可以看出，用户集合势估计方案减少了算法对采样次数的依赖，当采样次数较少时，性能提升明显。

图3　用户集合势估计算法性能Fig.3　Performance of USCE algorithms

图4　不同采样次数下的用户集合势估计算法性能Fig.4　Performance of USCE algorithms according to sample number

4　结束语

根据数据融合的合作频谱感知理论，提出了基于GEEF，SPEEF等方案的用户集合势估计合作频谱感知算法，通过估计算法估计出用户的集合势，再筛选出相应个数的最优数据生成最优GTS。仿真结果表明，在不需要任何先验信息的条件下，实际情况下的BUSCE方案感知性能优于原始BCED方案，并接近需要预知噪声功率的EGC方案；理想情况下的OUSCE方案感知性能也要优于OCED方案。并且，在采样次数较少时，用户集合势估计方案能够获得较好的感知性能。因此，基于用户集合势估计的合作频谱感知方案具有很强的实际应用价值。

[1]HAYKINS.Cognitiveradio:brainempoweredwirelesscommunication[J].IEEEJournalonSelectedAreasinCommunications, 2005, 23(2): 201-220.

[2]CABRICD,TKACHENKOA,BRODERSENRW.Spectrumsensingmeasurementsofpilot,energy,andcollaborativedetection[C]//IEEE.MilitaryCommunication.Conf.(MILCOM).Washington:IEEEPress,2006:1-7.

[3]ZENGYonghong,LIANGYingchang.Eigenvalue-basedspectrumsensingalgorithmsforcognitiveradio[J].IEEETransactionsoncommunications, 2009, 57(6):1784-1793.

[4]KAYSM.FundamentalsofStatisticalsignalprocessing,Volume2:DetectionTheory[J].BlindEqualization&SystemIdentification, 1969, 1(213):83-182.

[5]ZENGYonghong,KOHChooleng,LIANGYingchang.Maximumeigenvaluedetection:theoryandapplication[C]//IEEE.InternationalConferenceonCommunications.Beijing:IEEEPress, 2008: 4160-4164.

[6]ZHANGRui,LIMTJ,LIANGYingchang,etal.Multi-antennabasedspectrumsensingforcognitiveradios:AGLRTapproach[J].IEEETransactionsonCommunications, 2010,58(1):84-88.

[7]王颖喜, 卢光跃. 基于最大最小特征值之差的频谱感知技术研究[J].电子与信息学报, 2010, 32(11):2571-2575.

WANGYingxi,LUGuangyue.Basedonthedifferencebetweenmaximumeigenvalueandminimumeigenvaluespectrumsensingresearch[J].JournalofElectronics&InformationTechnology, 2010, 32(11):2571-2575.

[8]BOLLIGA,MATHARR.MMMEandDME:Twoneweigenvalue-baseddetectorsforspectrumsensingincognitiveradio[C]//IEEE:GlobalConferenceonSignalandInformationProcessing.Washington:IEEEPress, 2013: 1210-1213.

[9]ZENGYonghong,LIANGYingchang,ZHANGRui.BlindlyCombinedEnergyDetectionforSpectrumSensinginCognitiveRadio[J].IEEESignalProcessingLetters,2008, 15(6):649-652.

[10]XIEZhibin,TIANYubo,YANPeiyu,etal.Userselectionalgorithmformulti-userMIMOsystem[J].ComputerEngineeringandApplications,2012,45(28):107-111.

[11]GODARZIDM,ARSHADK,YOUNGWOOKKo,etal.SelectingUserinEnergy-EfficientCollaborativeSpectrumSensing[C]//IEEEWirelessCommunicationsandNetworkingConference:PHYandFundamentals.Detroit:IEEEPress, 2012: 1029-1033.

[12] 申滨,喻俊,黄琼,等. 基于EEF准则的认知无线电无线电宽带频谱感知[J]. 北京邮电大学学报, 2014, 37(6):115-119.

SHENBin,YUJun,HUANGQiong,etal.EEFcriterionbasedwidebandspectrumsensingusedincognitiveradio[J].JournalofBeijingUniversityofPostsandTelecommunications, 2014, 37(6): 115-119.

[13]KAYS.Exponentiallyembeddedfamilies-newapproachestomodelorderestimation[J].IEEETransactionsonAerospaceandElectronicSystems,2005,41(1):333-344.

[14]QUANZhi,CUIShuang,SAYEDAH.Optimallinearcooperationforspectrumsensingincognitiveradionetworks[J].IEEEJournalofSelectedTopicsinSignalProcessing, 2008, 2(1): 28-40.

[15]LIUSiyang,SHENJunyang,ZHANGRanran.Informationtheoreticcriterionbasedspectrumsensingforcognitiveradio[J].IETCommunications,2008,2(6):753-762.

[16]XUCuichun，KAYS.SourceEnumerationviatheEEFCriterion[J].SignalProcessingLetters,IEEE, 2008, 15(13):567-572.

[17]QINGHaobo,LIUYuanan,XIEGang.Robustspectrumsensingforblindmultibanddetectionincognitiveradiosystems:aGerschgorinlikelihoodapproach[J].KSIITransactionsonInternetandInformationSystems, 2013, 7(5): 1131-1145.

申滨(1978-)，男，贵州人，教授，博士，主要研究方向为移动通信技术、通信信号处理。E-mail:shenbin@cqupt.edu.cn。

高凯(1990-)，男，河北人，硕士研究生，主要研究方向为认知无线电频谱感知。E-mail:gaokai_2015@foxmail.com。

(编辑：田海江)

s：The National Natural Science Foundation of China(61201205,61379159)

User set cardinality estimation based cooperative spectrum sensing in cognitive radio

SHEN Bin, GAO Kai, HUANG Xiaoge, CHEN Qianbin

(Key Lab of Mobile Communication Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R.China)

Spectrum sensing is a basic function of cognitive radio systems, and the premise on which dynamic access to licensed spectrum and spectrum sharing are realized. In this paper, cooperative spectrum sensing scheme based on user set cardinality estimation in cognitive radio network is proposed. The scheme aims to estimate the set cardinality, which is optimal user number, fitting for participating in cooperative spectrum sensing through GEEF and SPEEF algorithms, then select corresponding spectral observation data to take part in generating final global test statistic, and finally make decisions about the existence of primary users by comparing with the decision threshold. Theoretical analysis and experimental results verify that the proposed algorithm can effectively improve the performance of spectrum sensing.

cognitive radio; cooperative spectrum sensing; user set cardinality estimation; user selection

10.3979/j.issn.1673-825X.2016.05.010

2015-10-08

2016-06-15通讯作者：申滨shenbin@cqupt.edu.cn

国家自然科学基金项目(61201205,61379159)

TN929.5

A

1673-825X(2016)05-0672-08