基于EMD与奇异值差分谱的侧信道信号特征提取
姚艳丽,吴震,饶金涛,王敏,杜之波
(成都信息工程大学信息安全工程学院,四川 成都 610225)
基于EMD与奇异值差分谱的侧信道信号特征提取
姚艳丽,吴震,饶金涛,王敏,杜之波
(成都信息工程大学信息安全工程学院,四川 成都 610225)
为了从强烈的背景噪声中提取侧信道信号的特征信息,提出了一种基于经验模式分解(EMD)与奇异值差分谱相结合的信号特征提取方法。该方法首先对原始侧信道信号进行EMD分解,计算各个特征模态函数(IMF)与原始信号的相关系数,找到最大相似特征分量;再对该分量进行奇异值分解求出对应的奇异值差分谱;最后根据差分谱进行重构和消噪,进一步提取分量的特征信息。实验结果表明,该方法可以有效应用于侧信道信号的特征提取,成功提高信号的信噪比和攻击成功率。
侧信道信号;经验模式分解;奇异值差分谱;特征提取;攻击成功率
1 引言
侧信道攻击(SCA, side channel attack)[1,2]是通过密码设备在软、硬件实现中泄露的执行时间、功率消耗或电磁辐射等侧信道信息而获取密钥的攻击手段。SCA的方法种类繁多,常见的有故障攻击、计时攻击、能量攻击等,其中,能量攻击作为一种高效的攻击方式受到了高度的重视。然而,在多数情况下,信号容易被噪声淹没导致有用信息无法提取,攻击成功率低,因此,需要采用信号处理技术来进行辅助处理。
近年来,国内外许多学者对侧信道信号的特征提取方法进行了研究。2014年,黄永远等[3]提出频域辅助分析的滤波方法,该方法证实了低通滤波后的信号攻击效率最高。2015年,蔡琛等[4]提出主成分分析的方法,该方法通过提取信号中的主成分来提高攻击效率。2015年,王喆等[5]提出重采样的频域滤波方法,该方法成功提高了攻击效率。CHES 2015会议上,Santos等[6]提出奇异谱分析的方法,该方法虽能通过提取时间序列的不同特征成分来提高信号的信噪比,但在奇异值分解的重构中仅凭先验知识对有效奇异值的数目进行选择。如何从非平稳且含噪的侧信道信号中提取出特征信息是提高信号信噪比和攻击成功率的关键。
本文针对侧信道泄露信号信噪比很低、攻击成功率不高和难以有效选择奇异值个数的问题,提出一种基于经验模式分解(EMD, empirical mode decomposition)和奇异值差分谱相结合的特征提取方法。该方法首先通过EMD分解得到原始信号的各个特征模态函数(IMF, intrinsic mode function),并利用相关系数法找到最大相似特征分量;再对该分量应用奇异值差分谱进行消噪和重构,进一步对原始时间序列不同成分的特征信号进行提取;最后进行相关性能量分析攻击。实验结果表明,该方法能够成功提取出信号的特征信息,有效提高信号的信噪比,在攻击效率和成功率上都取得了比较显著的进步。
2 基本理论
2.1 EMD分解方法
EMD分解方法[7~9]在1998年首次被提出,它在对信号进行分解时不需要事先设定基函数,突破了传统傅里叶变换的局限思维,在分析处理非线性非平稳信号上具有更加显著的优势,一经提出就在很多工程领域得到了广泛应用。
EMD分解的基本思想是将一个频率不规则的信号转化成多个单一频率的信号与残波。该方法的关键是将复杂的信号分解为有限个特征模态函数,而IMF分量必须具备以下2点:1) 在整个时间历程内,极值点数等于零点数或两者之差最多不超过1;2) 信号上极大值点形成的上包络线轴对称于极小值点形成的下包络线。具体分解过程如下。
Step1 找出原始信号s(t)上的全部极大值点和极小值点,运用3次样条函数对极大(小)值点进行拟合,得到原始信号的上下包络线,求出上下包络线的均值m1(t)。
Step2 从原始信号s(t)中去除m1(t)得到h1(t)。理论上,h1(t)是原始信号的一个分量,但一般而言,h1(t)不符合IMF的条件,因此,把h1(t)当作新的s(t)重复Step1i次,当hi(t)满足IMF的要求时,hi(t)即为EMD分解得到的第一个最高频率分量IMF,记作c1(t)。
Step3 用数据s(t)减去c1(t)得到一个差值信号r1(t),把r1(t)当作s(t)进行上述Step1和Step2 n次,获得n个IMF分量,当第n个分量(单调函数)不可再分时,终止循环。
Step4 经过以上过程,原始信号s(t)可表示为
其中,ci(t)为原始信号在不同频率段上的各个IMF分量,rn(t)为残余分量。
2.2 奇异值差分谱原理
1975年,De Prony等首次提出奇异谱分析(SSA, singular spectrum analysis)的概念,直到1986年,该方法被Broomhead等[10]应用于动力系统研究中后才受到人们的普遍关注。目前,SSA已经成功地应用到许多不同的领域。
奇异谱分析[11]适用于从短时非线性平稳时间序列中提取有用信息,但在奇异值分解重构时,有效奇异值个数的选择难以确定。而差分谱的应用可以有效解决信号在重构过程中奇异值个数选择的难题。奇异值差分谱主要根据特征信号与噪声之间具有能量可分性,对有噪信号构建的时滞矩阵进行奇异值分解,求出对应的差分谱[12,13],再根据差分谱对分解出的特征信号进行重构。具体过程描述如下。
1) 分解
Step1 构造时滞矩阵。对于给定的时间序列l=(l1,l2,…,lN),选择合适的窗口长度,根据时滞向量li=(l,l,…,l)T,1≤i
ii+1i+W -1≤D,D=N-W+1,构建时滞矩阵,即Hankel矩阵。
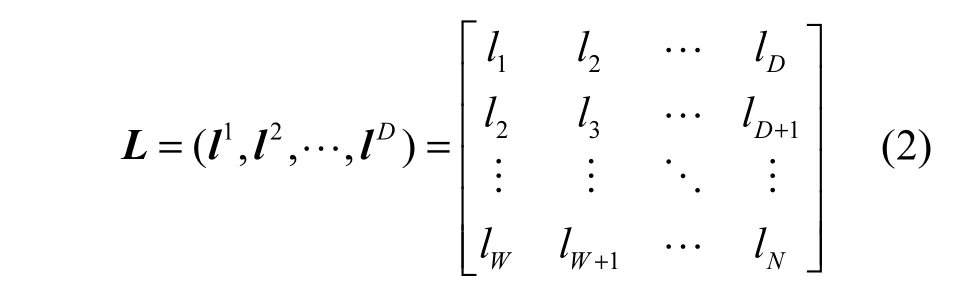
由于窗口长度对SSA的分解和重构很关键,太大或太小都会导致分量的重构困难,因此,选择最优的窗口长度值十分必要。通常,由式(3)的经验法则计算最佳窗口长度[14]
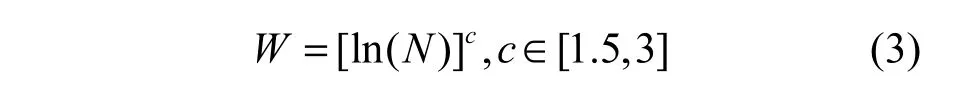
Step2 奇异值分解。由L和L的转置矩阵LT,求出L的自协方差矩阵LLT的特征值λ和特i征向量ui,其中,特征值为λ1,λ2,…,λW,且λ1≥λ2≥…≥λW≥0,对应的特征向量依次为u1,u2,…,uW。假设特征值不为0的个数最多为d,那么时滞矩阵可表示为
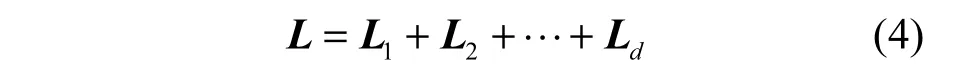
Step3 计算奇异值差分谱。奇异值序列的突变状况可以由差分谱描述,其定义为
所有βi构成的序列B=[β1,β2,…,βW-1]为奇异值的差分谱序列。与特征信号相比,噪声明显小于其所占的比重,因此,在它们的分界处存在较大的波动。即当相邻的2个奇异值之间差别很大时,在整个差分谱序列中会产生一个最大的尖峰βk。由于噪声普遍集中于最大峰值后,邻近的奇异值间差值较小,没有明显的峰值波动,故有用信号和噪声可通过最大峰值点k来分离。最大峰值点以前的k个奇异值对应的分量即为本文所需的有用信号,而噪声则与此相反。
2) 重构
Step1 分组。根据分解过程中Step3奇异值差分谱序列中最大峰值点的位置,确定该选取的分量进行重构。此选取分量的过程即为分组。
Step2 对角平均。将本过程Step1中选择的分量转化形成一个新的长度为N的时间序列,即重构。令Lp=min(W,D),Kp=max(W,D),根据对角平均公式将其转化为y1,y2,…,yN的时间序列,对角平均公式的展开式如下
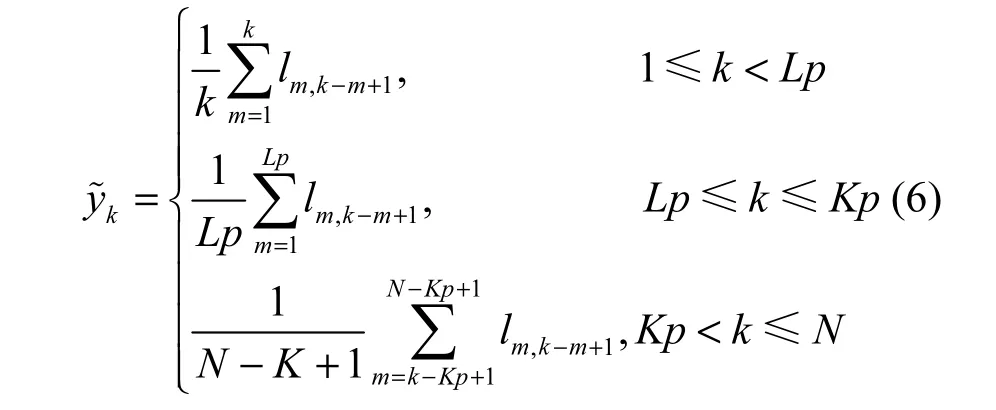
则y=(y1,y2,…,yN)即为重构后的时间序列。
2.3 相关性能量分析攻击原理
2004年,Brier等[15]提出了相关性能量分析(CPA, correlation power analysis)攻击,该攻击方法主要利用统计学中的皮尔逊相关系数ρ进行攻击。其攻击过程描述如下。
Step1 选择被执行算法的某个中间值。
Step2 输入明文,采集加密时的m组能量曲线,每组曲线n个采样点,建立实测的能量消耗矩阵Xm×n。
Step3 以汉明重量为攻击模型,猜测密钥,计算中间值的汉明重量,得到假设的能量消耗矩阵Hm×256。
Step4 根据式(7)计算实测的能量消耗矩阵与假设的能量消耗矩阵之间的相关系数,得到正确的猜测密钥。
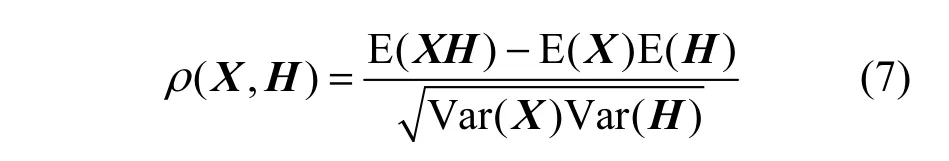
其中,Var(·)与E(·)分别表示方差及均值。当假设能量消耗与实测能量消耗之间达到最大相关性时,对应的猜测密钥即为正确的密钥。
3 侧信道信号特征提取方法
在真实的侧信道环境中采集的侧信道信号通常是非线性非平稳的信号,信噪比很低,用于攻击测试时的攻击成功率不高。EMD依据数据自身的特性能够自适应地将非平稳的信号分解为多个频率从高到低的平稳、线性的IMF分量,但由于强烈的背景噪声的影响,提取出IMF分量中的特征信息不够明显,攻击成功率不够理想。奇异值差分谱适用于对平稳的信号进行处理,它不仅可以降维,减少攻击测试时的运算量,而且能够有效消除信号噪声,进一步提取显著性信息。同时,差分谱的应用还能够有效解决信号在重构时奇异值个数难以确定的难题。因此,二者相结合计算更简便,适用范围更广,提取出的特征信息更明显,攻击的成功率更高。基于上述分析,本文提出了一种基于EMD与奇异值差分谱相结合的侧信道信号特征提取方法。该方法的基本思路如图1所示。
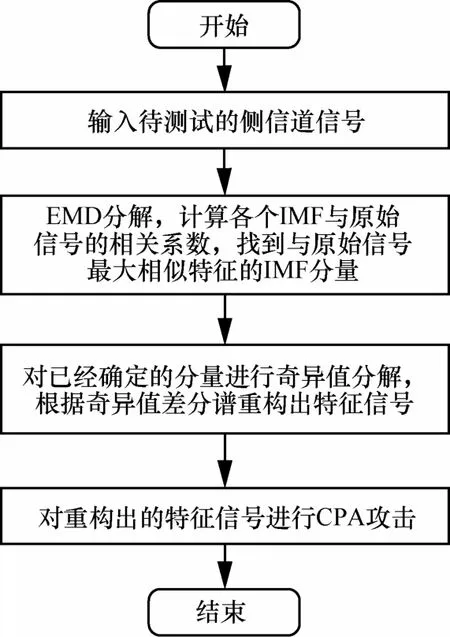
图1 侧信道信号特征提取方法流程
基于EMD与奇异值差分谱的侧信道信号特征提取方法如下。
Step1 对待测试的侧信道泄露信号进行EMD分解得到有限个IMF分量,观察各个分量的特征,计算各个分量与原始信号的相关系数,找到与原始信号最大相似特征的分量。
Step2 对已经确定的分量构建时滞矩阵,进行奇异值分解,求出奇异值差分谱,根据差分谱确定出重构信号的分量个数,消噪并进行重构,得到能表征原始序列不同成分的特征信号。
Step3 对提取出的有用信号进行CPA攻击。
4 攻击实验与分析
本文的实验环境为Inspector SCA平台,研究对象为智能卡上软实现的SM4密码算法的侧信道信号,选择的攻击点为SM4密码算法的S盒输出,本实验以攻击第一轮为例进行说明,第一轮的轮密钥rk0=0xF12186F9。整个实验包括侧信道信号采集、信号特征提取以及相关性能量分析攻击3部分。
4.1 侧信道信号采集
采集的10 000条SM4的侧信道信号如图2所示。
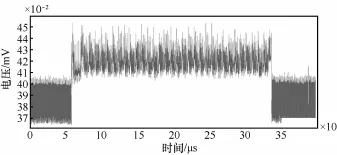
图2 原始侧信道信号
4.2 信号特征提取
1) EMD分解处理
根据第2.1节所述的原理对原始侧信道信号进行EMD分解。由于EMD的分解是一个不断迭代的过程,实验发现,无论对原始信号分解几层,分解后最后一层(即低频)的特征与原始信号的特征相似性最大。以EMD分解4层为例进行分析,分解后得到的各层IMF分量如图3所示。
观察图3中各个IMF分量的特征,根据式(7)计算各个IMF分量与原始信号的相关系数。其中,第4个分量与原始信号的相关性系数最大,为0.87,说明低频分量具有最大特征信息,因此将该分量作为下一步研究的对象。
2) 奇异值差分谱处理
根据第2.2节所述的原理对EMD分解处理后已确定的分量构建时滞矩阵进行奇异值分解,得到的奇异值序列和奇异值差分谱序列分别如图4和图5所示。
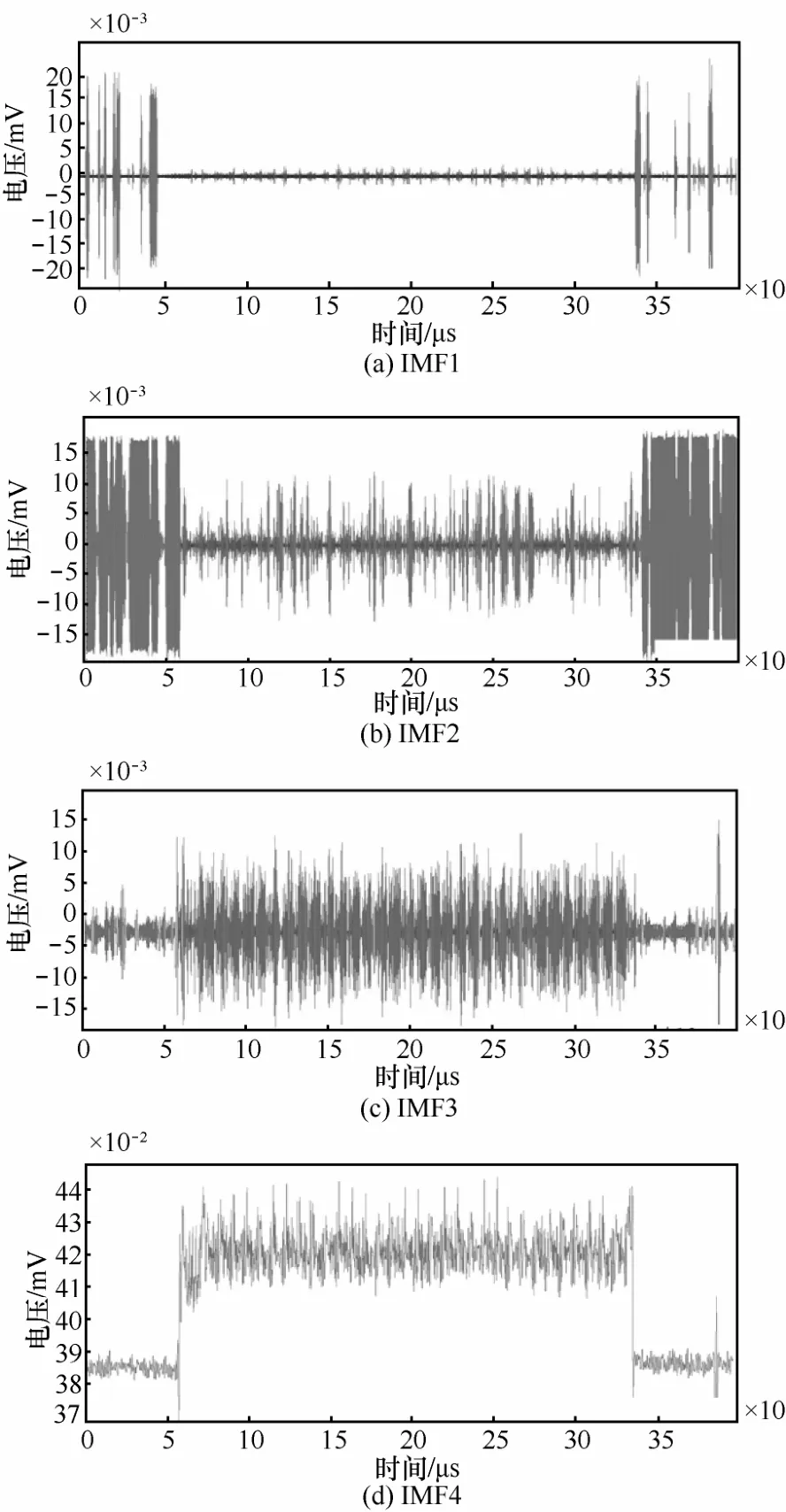
图3 EMD分解后的各层IMF分量
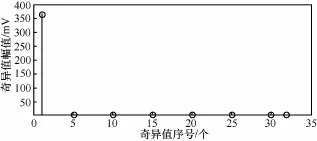
图4 奇异值序列
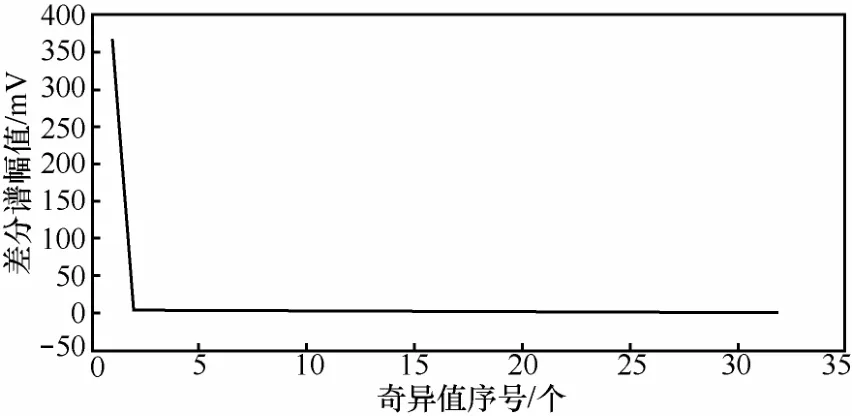
图5 奇异值差分谱序列
从图4中可见,该能量信号共有32个特征值,即该信号由32个成分组成。由图5可知,该信号在第一个点处出现了最大尖峰,表明有用信号和噪声在该位置有最大程度的分离。因此,提取相应的第1个分量进行重构,重构后的信号如图6所示。
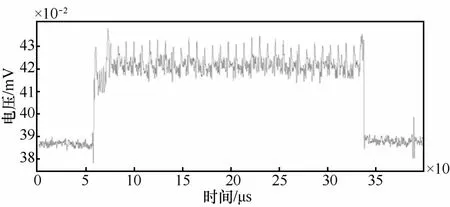
图6 重构第1个分量后的能量信号
当仅凭先验知识对第4个分量进行重构时,得到的重构信号如图7所示。
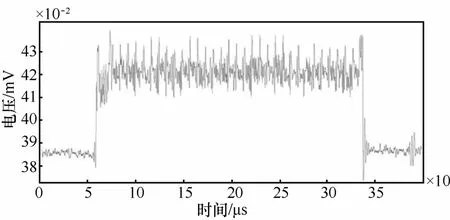
图7 仅凭先验知识重构后的能量信号
分别将图6、图7和图2对比可知,重构信号均和原始信号形状相同,没有相位偏移,信噪比有极大的提高。对比图6和图7可知,在奇异值分解的重构中运用差分谱进行重构,效果更显著,信噪比提高更大,有效解决了重构时奇异值个数选择的难题。
4.3 攻击结果与分析
以SM4加密算法的第一轮作为分析比较对象,分别对原始信号、EMD处理后的信号和利用差分谱重构后的信号的第一轮实施CPA攻击,攻击结果如表1所示。
通过对比表1中的相关性系数可知,EMD方法在一定程度上可以提取信号的有用信息,降低信噪比,但信号经过EMD及奇异值差分谱处理后相关性系数上升幅度更大,信号的信噪比提高更多。
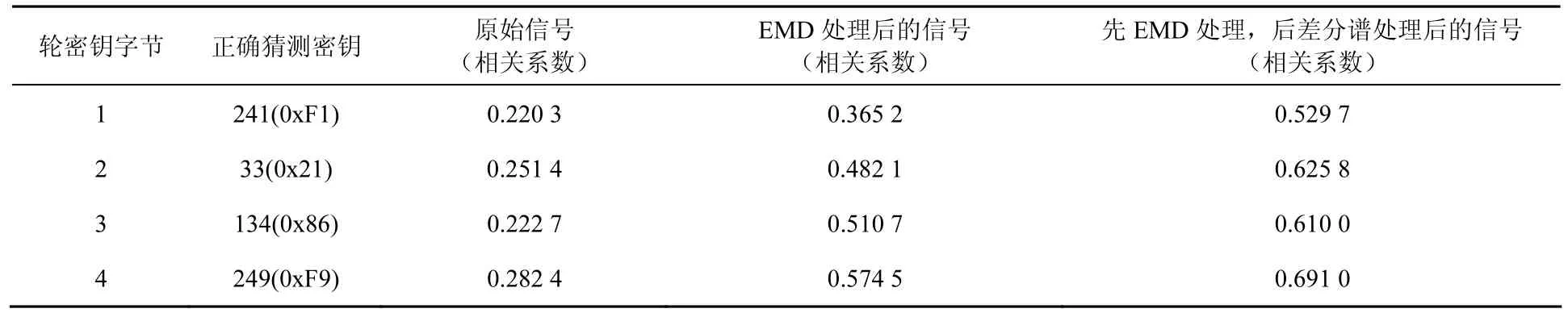
表1 SM4算法第一轮攻击结果对比
为了进一步证实该方法的有效性,实验采集了多组侧信道信号,分别采用传统方法、EMD方法与本文所提方法实施攻击,得到的攻击成功率与能量曲线数之间的关系如图8所示。
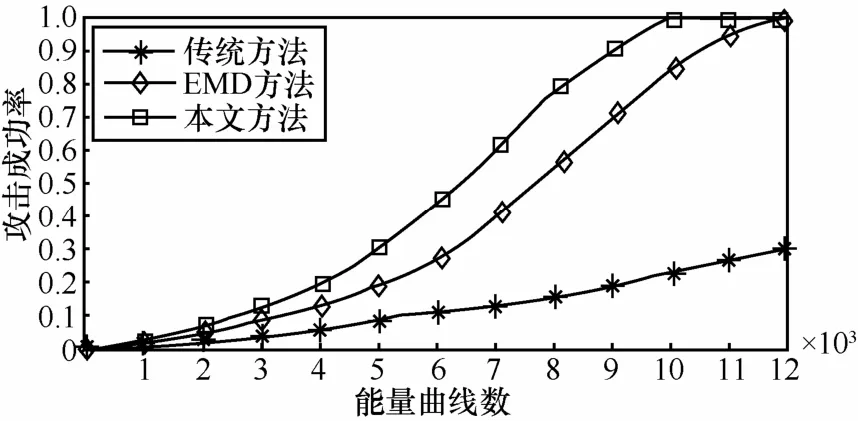
图8 能量曲线数与攻击成功率关系
由图8可知,使用本文方法处理后,大大减少了攻击所需的曲线数,攻击成功率要高于传统方法及EMD方法,达到了预期的效果。
5 结束语
为了提高能量泄露信号的信噪比和有效选择奇异值的个数,本文提出了一种基于EMD与奇异值差分谱相结合的侧信道信号特征提取方法。对在软实现上采集的信号分别采用传统方法、EMD方法和本文所提方法实施攻击并进行对比实验。实验结果表明,虽然3种方法都可以成功恢复出算法的全部密钥值,但本文方法不仅克服了传统依靠经验选择奇异值个数的缺点,还能更加有效地提取信号的特征信息,提高信号的信噪比,大大减少了攻击所需的曲线数,在攻击效率和成功率上都要优于传统方法。
[1] KOCHER P, JAFFE J, JUN B. Differential power analysis[C]//The 19th Annual International Cryptology Conference on Advances in Cryptology.c1999.
[2] 刘洋.关于侧信道攻击及其对策的一点探讨[J].警察技术,2014(S1):26-28. LIU Y. The discussion about side channel attacks and its countermeasures[J]. Police Technology, 2014(S1):26-28.
[3] 黄永远, 陈运, 陈俊, 等. 运用频域辅助分析的AES算法相关功耗攻击[J].四川大学学报(自然科学版),2014,51(3): 459-466. HUANG Y Y, CHEN Y, CHEN J, et al. CPA for AES by using frequency domain auxiliary analysis [J]. Journal of Sichuan University(Natural Science Edition), 2014, 51 (3):459-466.
[4] 蔡琛, 陈运, 万武南, 等.基于主成分分析的AES算法相关功耗分析攻击[J].电子技术应用,2015,41(8):101-105. CAI C, CHEN Y, WAN W N, et al. Correlation power analysis for AES based on principal component analysis [J]. Application of Electronic Technique, 2015, 41(8):101-105.
[5] 王喆, 王飞宇, 刘剑峰, 等. 基于重采样的差分频域分析方法[J].计算机学报, 2015,38(4):783-792. WANG Z, WANG F Y, LIU J F,et al. Differential frequency analysis method based on resample[J]. Chinese Journal of Computers, 2015, 38(4):783-792.
[6] SANTOS M D P, STANDAERT F X. Blind source separation from single measurements using singular spectrum analysis[M]// Cryptographic Hardware and Embedded Systems—CHES 2015. Berlin Heidelberg: Springer, 2015:42-59.
[7] HUANG N E,SHEN Z,LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].The Royal Society, 1998,454(1971): 903-995.
[8] 王唯嘉, 肖明清, 张磊, 等. 多小波包下经验模态分解去噪研究[J]. 计算机工程,2015,41(12):125-129. WANG W J, XIAO M Q, ZHANG L, et al. Research on empirical mode decomposition denoising under multiwavelet packet[J].Computer Engineering, 2015, 41(12):125-129.
[9] 陈可, 李野, 陈澜. EEMD分解在电力系统故障信号检测中的应用[J].计算机仿真,2010,27(3):263-266. CHEN K, LI Y, CHEN L. Ensemble empirical mode decomposition for power quality detection applications [J].Computer Simulation,2010, 27(3):263-266.
[10] BROOMHEAD D S. KING G P. Extracting qualitative dynamics from experimental data[J]. Physica D Nonlinear Phenomena, 1986,20(S2/3):217-236.
[11] 卢辰龙. 奇异谱分析在大地测量时间序列分析中的应用研究[D].长沙:中南大学, 2014. LU C L. Research on the application of singular spectrum analysis in geodetic survey time series[D]. Changsha: Central South University, 2014.
[12] 张文斌. 奇异值能量差分谱在信号降噪中的应用[J].工矿自动化,2014,40(10): 25-28. ZHANG W B. Application of energy difference spectrum of singular value in signal noise reduction [J]. Industry and Mine Automation, 2014, 40(10):25-28.
[13] 王志武,孙虎儿,刘维雄. 基于局部均值分解和奇异值差分谱的滚动轴承故障诊断研究[J]. 机械科学与技术, 2014, 33(9):1340-1344. WANG Z W, SUN H E, LIU W X. Study on rolling bearing fault diagnosis based on lmd and difference spectrum theory of singular value[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(9):1340-1344.
[14] POSKITT D S. Window length selection and signal-noise separation and reconstruction in singular spectrum analysis[J]. Monash Econometrics & Business Statistics Working Papers, 2011.
[15] BRIER E, CLAVIER C, OLIVIER F. Correlation power analysis with a leakage model[C]//Cryptographic Hardware and Embedded System-CHES 2004 Lecture Note in Computer Science. c2004: 16-29.

姚艳丽(1991-),女,湖北枝江人,成都信息工程大学硕士生,主要研究方向为信号处理、信息安全、侧信道攻击与防御。

吴震(1975-),男,江苏苏州人,成都信息工程大学副教授,主要研究方向为信息安全、密码学、侧信道攻击与防御、信息安全设备设计与检测。

饶金涛(1985-),男,湖北黄冈人,硕士,成都信息工程大学助教,主要研究方向为信息安全、嵌入式系统安全、侧信道攻击与防御。

王敏(1977-),女,四川资阳人,博士,成都信息工程大学讲师,主要研究方向为网络攻防、侧信道攻击与防御。

杜之波(1982-),男,山东冠县人,硕士,成都信息工程大学讲师,主要研究方向为信息安全、侧信道攻击与防御、天线应用和物联网安全。
Feature extraction of side channel signal based on EMD and difference spectrum of singular value
YAO Yan-li, WU Zhen, RAO Jin-tao, WANG Min, DU Zhi-bo
(College of Information Security Engineering, Chengdu University of Information Technology, Chengdu 610225, China)
In order to extract feature information of side channel signal from the strong noise, the approach of signal feature extraction was proposed on account of empirical mode decomposition (EMD) and difference spectrum of singular value. Firstly, using EMD to decompose the original side channel signal, the correlation coefficient between all the intrinsic mode functions (IMF) and the original signal were calculated to find the component of biggest similar characteristic. Then, to make a singular value decomposition of IMF component and corresponding difference spectrum of singular values was obtained. Finally, according to the difference spectrum, the filtered and reconstructed signal of IMF component was obtained, and the feature information of component was further extracted. The actual examples show that the method can extract characteristic information of side channel signal validly and improve the SNR and success rate of attack of signal successfully.
side channel singnal, empirical mode decomposition, difference spectrum of singular value, feature extraction, attack success rate
s: The National Science and Technology Major Project (No.2014ZX01032401-001), The National High Technology Research and Development Program (863 Program) (No.2012AA01A403),“The 12th Five-Years” National Cryptogram Development Fund (No.MMJJ201101022), Sichuan Provincial Science and Technology Support Programmer(No.2014GZ0148), Sichuan Provincial Education Department Key Scientific Research Project (No.13ZA0091), The Scientific Research Foundation of CUIT (No.CRF201301), The Scientific Research Foundation of the Young and Middle-aged Academic Leaders of CUIT (No.J201610)
TP309/TN911
A
10.11959/j.issn.2096-109x.2016.00069
2016-05-27;
2016-06-22。通信作者:吴震,wzhen@cuit.edu.cn
国家重大科技专项基金资助项目(No.2014ZX01032401-001);国家高技术研究发展计划(“863”计划)基金资助项目(No.2012AA01A403);“十二五”国家密码发展基金资助项目(No.MMJJ201101022);四川省科技支撑计划基金资助项目(No.2014GZ0148);四川省教育厅重点科研基金资助项目(No.13ZA0091);成都信息工程大学科研基金资助项目(No.CRF201301);成都信息工程大学中青年学术带头人科研基金资助项目(No.J201610)

