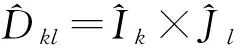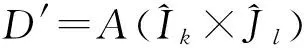递归分形插值曲面的变差

张文景,冯志刚

(江苏大学 理学院,江苏 镇江　212013)



递归分形插值曲面的变差

张文景,冯志刚

(江苏大学 理学院,江苏 镇江212013)

在求解函数图像维数过程中，分形插值函数的变差可以代替盒维数公式中最少盒子数,从另一个角度得到函数图像的盒维数公式.从研究二元连续函数的变差性质入手,给出了矩形区域上递归分形插值曲面(RFIS)的变差估计,为递归分形图形维数的研究提供一种新方法.

二元递归分形插值函数;二元连续函数;分形插值曲面;变差

MSC 2010：37C45;28A80;41A05

分形插值是分形几何理论及其应用研究中的一个重要内容,由美国数学家Barnsley[1]首先提出,在图像压缩、非光滑曲线和曲面的拟合等研究领域中显示出了独特的优越性.1989年,在原分形插值的基础上Barnsley[2]首先介绍递归分形插值函数并给出平面上递归分形插值函数图像的计盒维数公式.和传统的插值函数相比,递归分形插值函数是发展起来的一种更灵活、更优越的分形插值函数,更能刻画出自然界中复杂的随机性和不确定性.沙震等[3]对Barnsley的递归FIF(分形差值函数)分形维数加以改进,去掉关联矩阵不可约的限制条件,得出新的维数公式.

变差是刻画粗糙程度的一种重要参数,用来研究各种尺度下函数的粗糙度,而粗糙度在材料学、力学等学科领域中有着非常广泛的应用[4-7].求分形图像的维数是分形理论研究的重要内容,计算盒维数一般都是按照它的定义来证明的,即找出覆盖图像的最少盒子数.而引入变差的概念,通过研究平面上连续分形函数的变差性质,可以得到平面上连续函数图像的计盒维数计算公式,为计算函数图像的计盒维数提供了新的工具.

文志英[8]研究了平面上连续函数变差的性质,并给出平面上连续函数图像的计盒维数计算公式.冯志刚等[9]研究了一类分形插值函数δ-变差的性质,用δ变差代替维数定义中的最少盒子数,得到了一种证明分形图形维数的新方法.Feng[10]介绍了矩形区域上分形插值曲面的构造方法,并给出了二元连续函数的振幅以及变差的定义,证明了二元分形插值函数变差的一些性质,并运用连续函数图像的盒维数与变差的关系,得出了分形曲面的维数公式.徐惠等[11]讨论了一类网格上二元连续分形插值曲面,研究二元连续函数的振幅与变差性质,给出变差估计从而得到分形插值曲面计盒维数的准确值.王伟从连续函数的变差性质入手,得到了一元递归分形插值函数的变差性质,运用变差阶的估计得到递归分形插值曲线的维数定理.

本文在上述文献基础上讨论二元连续函数的变差性质,研究矩形区域上二元递归分形插值函数(δ,γ)变差的估计,为递归分形插值曲面的维数计算进一步提供理论基础.

1　二元递归分形插值函数

考虑矩形区域上的二元递归分形插值函数.给定闭区间I=J=[0,1],0=x0

(1)

其中sij为给定的常数,φij(x,y)为D上的二元连续函数.可得一个递归迭代函数系(RIFS)

(2)

(3)

其中对任意i,j=1,2,…,MN,规定

(4)

2　二元连续函数的变差

根据连续函数(δ,γ)-变差定义,Feng[10]证明了下面的引理.

引理1[10]令z=f1(x,y),z=f2(x,y)分别为D上的二元连续函数,C1,C2为给定的任意常数,有

1)Vc1f1+c2;δ,γ(D)=|c1|Vf1;δ,γ(D),

2)Vf1;δ,γ(D)-Vf2;δ,γ(D)≤Vf1+f2;δ,γ(D)≤Vf1;δ,γ(D)+Vf2;δ,γ(D).

引理2[10]令D=[a,b]×[c,d],z=f(x,y)为D上二元连续函数,a

(5)

其中Vf(D)=supDf(x,y)-infDf(x,y).

3　递归分形插值曲面的变差

(6)

其中s=A-1(x)∈Ik,t=B-1(x)∈Jl.在区间D′上,有

(7)

证由式(1)得

(8)

由式(8)和引理1 得

(9)

由定理1得

(10)

(11)

φij为D上的连续可微函数且φij⊂Pr,令Mij=max(x,y)∈I×J|φij(x,y)|,则

(12)

由引理2

(13)

由式(9-13)得不等式(7)左边可证.

由引理2得

(14)

类似地，由式(9-12)和式(14),可证不等式(7)右边.

[1]BARNSLEY M F.Fractal everywhere[M].New York:Academic Press,1988.

[2]BARNSLEY M F,ELTON J H,HARDIN D P.Recurrent iterated function systems[J].Constr Approx,1989,5:3-31.

[3]沙震,阮火军.Bamsley-Elton Hantin的一个定理的修正[J].高校应用数学学报A辑,2000,15(2):157-162.

SHA Z,RUAN H J.A revision of the theorem of the Bamsley-Elton Hantin[J].Appl Math J Chinese Univ Ser A,2000,15(2):157-162.

[4]TRICOT C.Curves and fractal dimension[M].New York:Spinger,1995.

[5]DUBUC B,TRICOT C.Variation d’une Function et Dimension de son graph[J].C R Math Acad Sci ParisSer I,1998,306:531-533.

[6]TRICOT C .Funtion norms and fractal dimension[J].Siam J Math Anal,1997,28(1):189-212.

[7]DUBUC B,ZUKER S W,TRICOT C,et al.Evaluating the fractal dimension of surfaces[J].Proc R Soc Lond Ser A,1989,425:113-127.

[8]文志英.分形几何的数学基础[M].上海：科学出版社,2000.

WEN Z Y.The mathematical basis of fractal geometry[M].Shanghai:Science Press,2000.

[9]冯志刚,王磊.分形差值函数的变差的性质[J].江苏大学学报(自然科学版),2005,26(1):49-52.

FENG Z G,WANG L.Properties of variation of fractal interpolation function[J].Journal of Jiangsu University(Natural Science),2005,26(1):49-52.

[10]FENG Z G.Variation and Minkowski dimension of fractal interpolation surface[J].Math Anal Appl,2008,345(1):3222-344.

[11]徐惠,冯志刚.一类分形插值函数的变差和计盒维数[J]．安徽工业大学学报(自然科学版),2008,25(4)：444-447．

XU H,FENG Z G.A class of variation and box-counting dimension of fractal interpolation function[J].Journal of Anhui University of Technology(Natural Science),2008,25(4)：444-447．

[12]王伟,冯志刚.递归分形插值函数的计盒维数[J].安徽工业大学学报(自然科学版)，2009,26(2):187-189.

WANG W,FENG Z G.Box-counting dimension of recurrent fractal interpolation function[J].Journal of Anhui University of Technology(Natural Science),2009,26(2):187-189.

[13]BOUBOULIS P,DALLA L.A general construction of recurrent bivariate fractal interpolation surfaces and computation of their box-counting dimension[J].Japprox Theory,2006，141：99-117.

(责任编辑：王兰英)

Variation of recurrent fractal interpolation surface

ZHANG Wenjing,FENG Zhigang

(College of Science,Jiangsu University,Zhenjiang 212013,China)

To calculate the dimension of grap of function, the minimum boxes can be replaced by the variation of fractal interpolation function, and the box-dimension formula can be proved from another angle.Based on the study of the properties of variation of bivariate continuous function,the variation of recurrent fractal interpolation function is estimated on the rectangular domain,which provides a new method to study dimension of recurrent fractal graph.

bivariate recurrent fractal interpolation function;bivariate continuous function;fractal interpolation surface;bivariate.

10.3969/j.issn.1000-1565.2016.04.003

2015-06-25

国家自然科学基金资助项目(51079064)

张文景(1988—)，女，江苏徐州人，江苏大学在读硕士研究生.E-mail:656780786@qq.com

冯志刚(1962—)，男，江苏常州人，江苏大学教授，主要从事分形几何理论的研究.E-mail:zgfeng@ujs.edu.cn

O184

A

1000-1565(2016)04-0349-04