利用室外旋转天线法估计导航卫星接收机天线相位中心偏差
张润涛,马德强
(1.信息工程大学 导航与空天目标工程学院,郑州 450052;2.61206部队,北京 100071;3.山东省地质测绘院,济南250011)
利用室外旋转天线法估计导航卫星接收机天线相位中心偏差
张润涛1,2,马德强3
(1.信息工程大学 导航与空天目标工程学院,郑州 450052;2.61206部队,北京 100071;3.山东省地质测绘院,济南250011)
导航卫星接收机的天线相位中心偏差是GNSS测量应用中必须考虑的一项误差。本文研究了在室外条件下利用旋转天线法测量和估计导航卫星接收机的天线相位中心偏差的理论和方法,并给出具体的操作步骤和相应的参数估计方法。算例采用位于西安某科研单位楼顶两台GPS/BDS双模卫星导航接收机组成超短基线,通过实测数据分别解算得到实验所用的接收机天线的BDS B1频率和GPS L1频率天线相位中心偏差的参考值,并进行精度分析,证明此方法是一种在实际应用中精度较高且操作性强的方法。
GNSS接收机;GPS/BDS;天线相位中心;超短基线;旋转天线法
0 引 言
GNSS测量是以接收机天线相位中心的精确位置为参照的,理论上相位中心与几何中心应保持一致,现实中由于相位中心会随信号输入的强度和方向不同而变化,即会随卫星高度角和方位角的变化而变化,通常称之为接收机天线相位中心偏差。它对GNSS定位影响可达数厘米,且很难通过差分的方式消除或减弱,它是制约GNSS精度提高的一个重要因素。模型改正是消除和减弱GNSS接收机天线相位中心偏差的一个很好的途径,本文尝试利用数学和物理模型来估计GNSS接收机天线相位中心偏差。
对于导航卫星接收机天线相位中心偏差的研究可以追朔到上世纪八十年代[1],在之后的应用中,Schupler[2]采用了在微波暗室内估计导航卫星天线相位中心误差的算法,国内一些学者也采用了微波暗室法(室内法)测定导航卫星天线相位中心误差[3-5]。同时,也有一些学者采用室外测定天线相位中心的研究[6-8],但仅仅是针对GPS卫星。相对于室内微波暗室天线相位中心估计方法,室外法具有对仪器设备要求不高、数据处理算法更简易、实际操作更容易实现等优点,且对提高定位精度有很好的效果。
从2000年至今,中国已发射19颗北斗导航卫星,并计划到2020年增加至35颗,目前对于GPS天线相位中心改正的研究已经有大量成果且较为成熟,而国内对北斗接收机天线相位中心误差研究开展的较少。本文从GNSS天线相位中心的相关改正和建模的理论出发,对北斗天线相位中心误差的估计方法进行初步的研究。
1 天线相位中心偏差产生的原因
在利用GNSS测量时,观测者获取的观测值通常情况下是以GNSS接收机天线的相位中心为参考点,从理论上讲,GNSS天线的几何中心和相位中心应保持一致,但GNSS的相位中心是随着可见卫星数量、方向、位置和信号强弱的变化而时刻变化的,即观测时相位中心的瞬时位置与理论上的相位中心位置将有所不同,通常称这种偏差为GNSS天线相位中心的位置偏差,如图1所示。它通常具有如下特点:1 )偏差数值和位置随时间变化; 2) 同一天线在地面不同位置时,偏差大小不同; 3) 定位影响可以达几毫米至几厘米。瞬时相位中心的位置很难确定,一般用求取相位中心偏差均值的方式来解决。
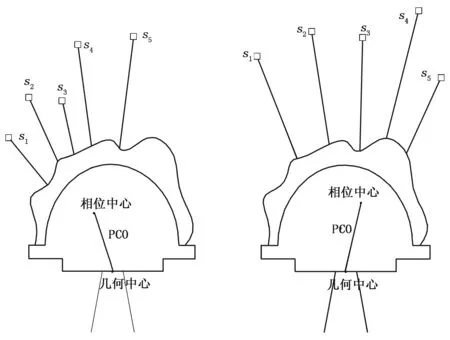
图1 同一GNSS接收机天线不同可视卫星条件时的天线相位中心偏差
2 室外旋转天线法及数据处理算法
2.1室外旋转天线法
采用室外旋转天线估计法,首先需要寻找一个视野开阔不受障碍物遮挡且无强磁场的平坦空地作为观测场,其次需要设置一个野外超短基线(通常指边长5~10 m的短基线),最后在基线两端安置GNSS接收机天线(通常选多频扼流圈天线)并严格整平,选择至少可视卫星大于5颗的时间段进行观测,每个时段至少2 h.
具体操作流程如下:
1) 在基线两端分别安置GNSS扼流圈天线,并精确对中、整平,在安置过程中,需要注意把天线的指北点朝向概略北方向;
2) 在两个天线指北的基础上,首先观测1个时段(2 h);
3) 在步骤2的基础上,保持天线A指向不变,天线B先后按顺时针方向旋转90°、180°和270°,并在三个方向各观测1个时段;
4) 同理,在保持天线B指向为北的情况下,天线A在顺时针旋转90°、180°和270°的位置上分别观测1个时段;
5) 观测完成后,分别解算各个时间段的基线坐标向量值。
2.2数据处理方法
如图2所示,GNSS接收机天线A与天线B分别安装于超短基线的两端。OA表示天线A的几何中心,OB表示天线B的几何中心。其中,A1为天线指北时天线A的平均相位中心,B1表示指北时天线B的平均相位中心。
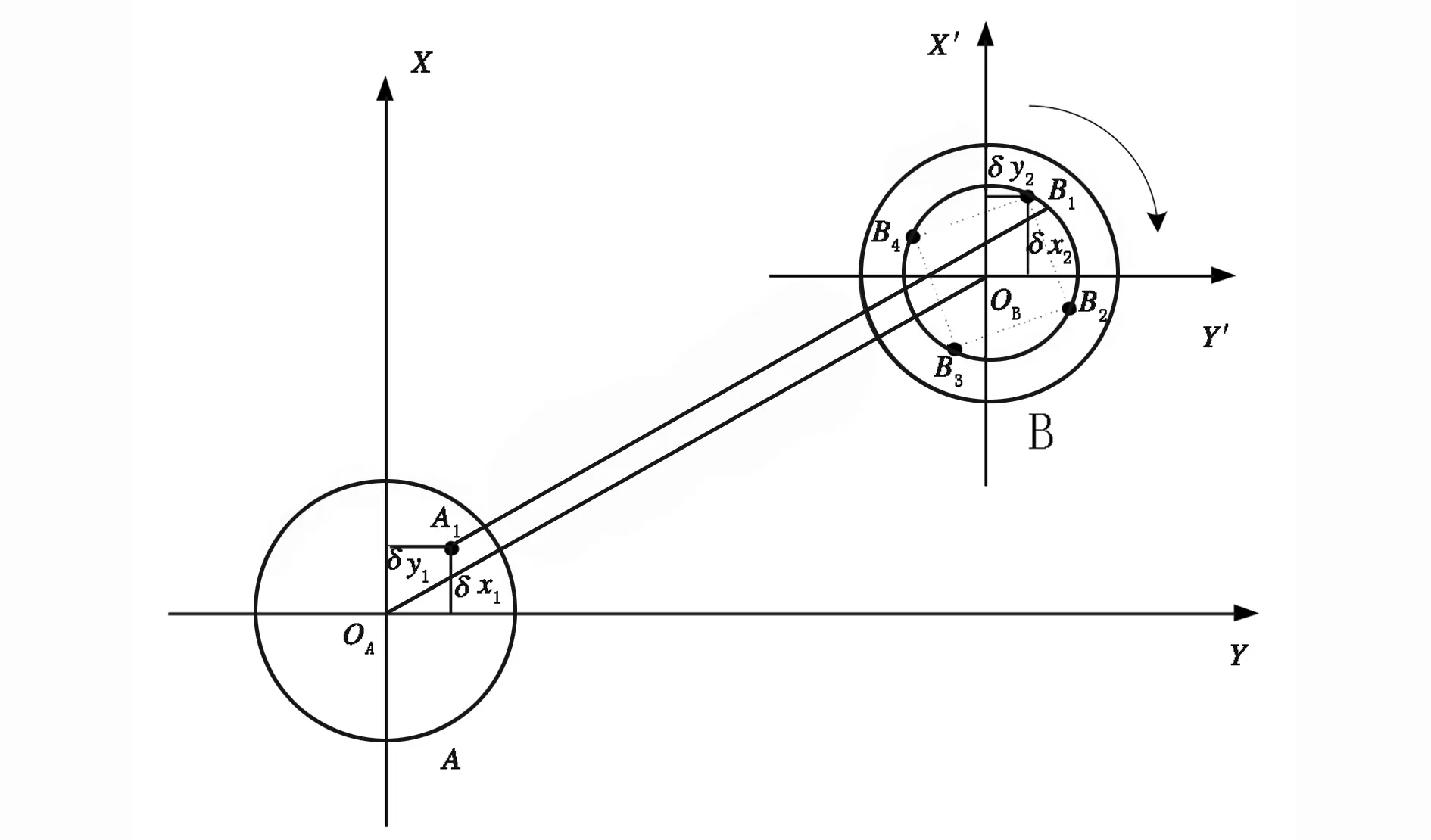
图2 天线A固定天线B旋转的测量示意图
以天线几何中心OA为原点,设OA与指北标志的连线为X轴,过OA的垂直方向为Z轴,Y轴与X、Z轴构成右手坐标系。同理,以OB为原点,建立X′OBY′坐标系。当两台GNSS天线同时指北时,在平面坐标系XOAY中GNSS天线A的平均相位中心A1为(δx1,δy1),在坐标系X′OBY′中天线B的平均相位中心B1为(δx2,δy2)。当天线A和B沿着顺时针依次旋转90°、180°、270°,其平均相位中心在各自坐标系中的坐标如表1所示。
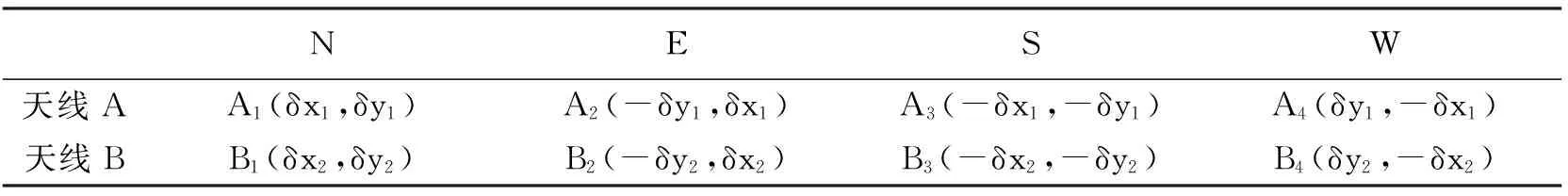
表1 天线在不同旋转位置的坐标
设Δx,Δy为天线A和B几何中心的坐标差值,dxi、dyi为基线第i个观测时段的x坐标差与y坐标差。当天线A固定指北,天线B旋转观测四个
时段(N→E→S→W)时,根据图2,可得如下残差方程:
(1)
同理,当天线B固定指北,天线A再旋转观测三个时段(E→S→W)时,残差方程为
(2)
联立两个残差方程,令
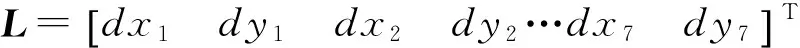
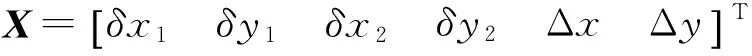
得简化的误差方程
V=L-BX,
(3)
其中,B为X的系数矩阵,dxi和dyi(i=1,2,…,7)可以通过基线解算求得。设P为单位权阵,则根据最小二乘法原理,误差方程的法方程为BTPBX=BTPL,进而可求解得到X.
3 实测算例分析
3.1试验准备与数据处理
实验采用两台TrimbleNETR9GPS/BDS双模接收机,所配天线类型为扼流圈天线(Trimble59900.00),试验地点为西安某研究所楼顶(视野开阔),如图3所示,实验时间为2014年1月8日的多个时段。
利用伯尔尼软件(Bernese5.1)进行超短基线的数据处理,采用GPS/BDS事后高精度的精密星历(****.sp3),并采用从IGS官网下载的极移参数等信息,对流层采用NIELL模型解算,模糊度固定采用QIF方法。在此基础上,分别计算GPSL1 频点和BDSB1频点的估计值。

图3 超短基线试验现场
3.2GPS L1 解算结果
对于GPS L1,基线解算结果如表2所示。
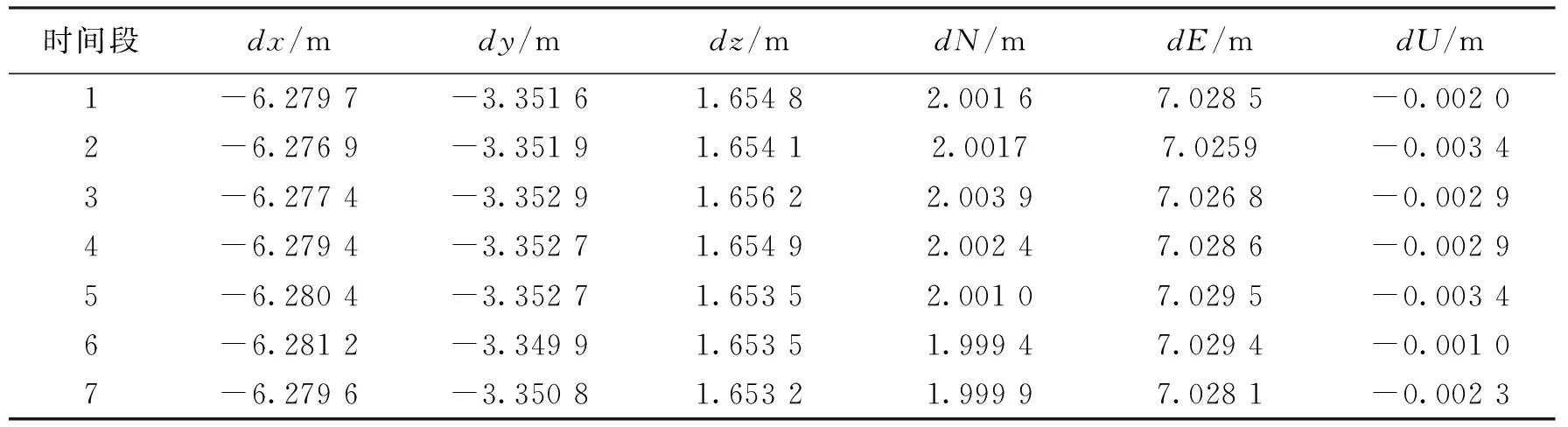
表2 GPS基线解算结果
由于两个GNSS天线是同一型号,则二者相位中心偏差基本相同,因此,可以把未知参数缩减为4个,即认为δx1与δx2、δy1与δy2相同。同时分析上表,不选用基线解算精度较差的第2、3时间段,求解结果为
δx=0.000808,δy=-0.000498,
Δx=2.001245,Δy=7.028360.
与IGS官网提供的天线相位中心改正文件比较,如表3所示。
通过表3分析可得,使用本文方法估计得到天线相位中心改正值与IGS提供的参考值基本一致,其存在的误差可能是测量时段不够多的原因导致。
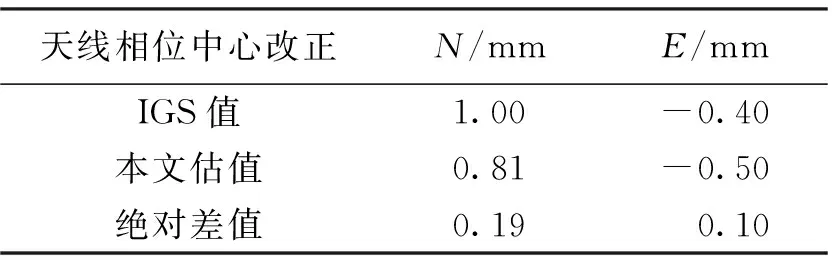
表3 GPS L1 PCO估值与参考值比较
3.3BDS B1 解算结果
对于BDS B1,基线解算结果如表4所示。
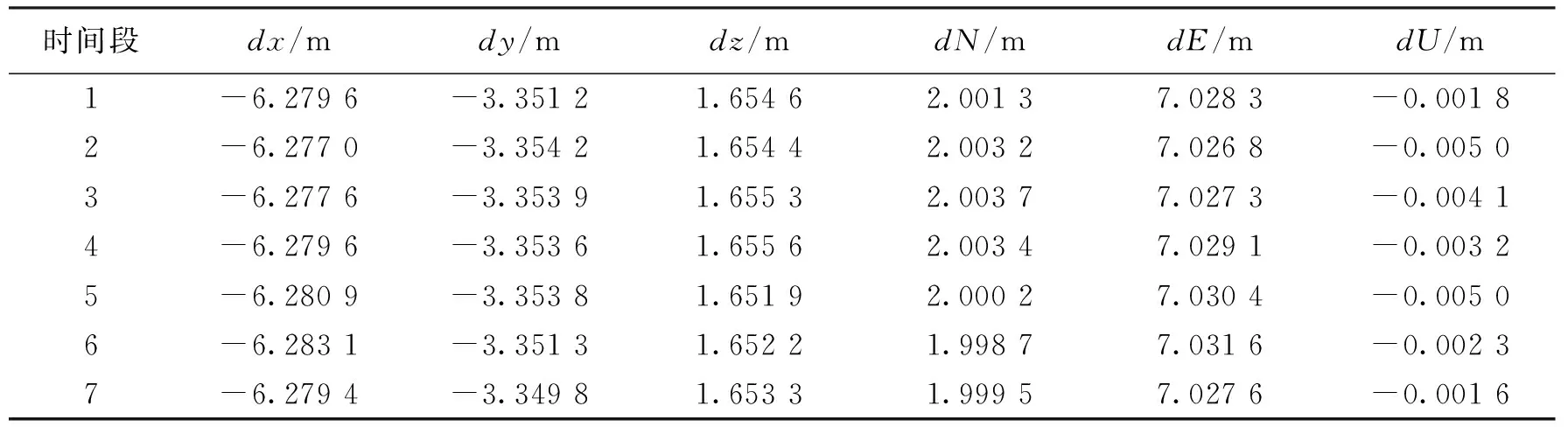
表4 BDS基线解算结果
与GPS解算策略相同,估计4个参数,不选用基线解算精度较差的第2、6时间段,求解结果为
δx=0.001338,δy=-0.000554,
Δx=2.001242,Δy=7.028383.
4 结束语
本文在旋转天线法相关理论的基础上,根据天线相位室外校正的实测结果,采用最小二乘法处理观测数据,得到相应GPS和BDS接收机天线的相位中心偏差。其中GPS的解算结果和IGS公布的参考值很接近,证实此方法的正确性和可行性。同时利用此方法求取了目前并没有发布的BDS B1频点的天线相位中心偏差,该方法可用于实际高精度BDS/GPS定位中,以进一步提高定位精度。
[1] SIMS M L. Phase center variation in the geodetic TI4100 GPS receiver system's conical spiral antenna[C]//In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System. Rockville, Maryland. U.S. Department of Commerce, May 1985.
[2] SCHUPLER B R, ALLSHOUSE R L, CLARKl T A.Signal characteristics of GPS user antennas [J].Inst Navigation,1994(41):277-295.
[3] 刘智超,张则宇,庞飞. GNSS天线相位中心偏差检定及不确定度分析[J]. 测绘地理信息, 2014(3):19-23.
[4] 张勇虎,周力,郑彬,等. 一种新的微波暗室天线相位中心标定方法[C]//2005全国微波毫米波会议,2006.
[5] 柯树人. 导航定位天线相位中心的实验室标定[C]//中国宇航学会飞行器测控专业委员会2007年航天测控技术研讨会, 2007.
[6] 郭金运,徐泮林,曲国庆. GPS接收机天线相位中心偏差的三维检定研究[J]. 武汉大学学报(信息科学版), 2004, 28(4):448-451.
[7] 高伟,晏磊,徐绍铨,等. GPS天线相位中心偏差对GPS高程的影响及改正研究[J]. 仪器仪表学报, 2008, 28(11):2052-2058.
[8] 魏锦德,黄张裕,海美,等. GPS天线相位中心误差的检测与改正[J]. 测绘科学技术学报, 2012, 29(6):410-413.
An Estimate of Navigation Satellite Receiver Antenna Phase Center Offset Based on the Outdoor Rotating AntennaMethod
ZHANG Runtao1,2,MA Deqiang3
(1.InformationEngineeringUniversity,Zhengzhou450052,China;2.61206Troops,Beijing100071,China;3.InstituteofGeologicalSurveyandMappinginShandong,Jinan250011,China)
The antenna phase center offset of navigation satellite receiver is a GNSS measurement error in applications, which must be considered. In this study, with outdoor conditions, the theory and methods of the rotating antenna phase center measurement and estimation for navigation satellite receiver were researched, andproposing the specific steps of corresponding parameter estimation method. The experiment wasoperated in Xi'an, onthe roof of a research unit, two GPS/BDS dual mode satellite navigation receivers composing USBL.By the measured data the authors calculate antenna phase center offsets respectively on the BDSB1 frequency and the GPS L1 frequency,and the precision analysisproves this method is a workable approach with high precision.
GNSS receiver; GPS/BDS; antenna phase center; ultra short baseline; rotating antenna method
10.13442/j.gnss.1008-9268.2016.04.004
2016-03-14
P228.4
A
1008-9268(2016)04-0017-05
张润涛(1985-),男,硕士,助理工程师,从事GNSS数据处理理论与方法研究。
马德强(1987-),男,硕士,工程师,从事GNSS数据处理理论与方法研究。
联系人: 张润涛 E-mail: zrt0206@126.com

