粒子群算法在边坡滑动面计算的可行解拟合修正★
邵 兆 通
(上海理工大学环境与建筑学院,上海 200093)
·岩土工程·地基基础·
粒子群算法在边坡滑动面计算的可行解拟合修正★
邵 兆 通
(上海理工大学环境与建筑学院,上海200093)
通过采用基于拟合优化的边坡滑动面粒子群算法,计算分析了无黏性土和黏性土边坡的安全系数和滑动面,通过FLAC3D计算结果对比,指出拟合修正的粒子群算法具有足够的精度和速度,对求解边坡最优滑动面有一定的指导意义。
粒子群优化,边坡稳定,滑动面,安全系数
0 引言
边坡稳定分析是岩土工程中的经典课题,由于实际工程的条件复杂性,不能通过约定唯一的条件推导具体求解滑动面和安全系数的公式。许多学者针对粒子群算法求解边坡稳定的滑动面问题进行了很多尝试。谢百义等[1]提出非圆弧滑动面的向量表示方法,结合了粒子群优化算法和遗传算法的优势形成新算法以搜索临界滑动面,该算法需要对可能出现的异常进行修正。陈云敏等[2]详细论述了粒子群算法搜索临界滑动面的原理,突出介绍了各条块之间所需要满足的约束关系,但并没有介绍在PSO算法中如何满足这些约束关系。杨善统等[3]基于变异和二次序列规划对粒子群优化算法进行改进,搜索临界滑动面,使粒子群算法更容易收敛于全局最优解,仅优化了算法,并没有研究粒子的约束条件。李亮等[4]提出了一种不连续飞行粒子群优化算法求解复杂边坡的临界滑动面,能够自动生成可行的滑动面,并利用Spencer法求解安全系数搜索临界滑动面,但该方法会降低安全系数的收敛速度和精度。本文提出基于拟合优化的边坡滑动面粒子群算法,既能够保证粒子群算法的寻优能力,又能够使生成的粒子均满足边坡滑动面约束条件,提高了滑动面的收敛速度和精度。通过无黏性土与黏性土边坡的计算表明,该算法具有较好的收敛速度和精度。
1 滑动面拟合优化
粒子群优化算法在边坡滑动面计算的应用中,粒子速度位置迭代需要满足边坡实际情况的约束条件,然而在粒子群算法的原理中,其速度仅与粒子的历史最优位置、个体最优位置、惯性因子等有关,可以首先严格按照粒子群算法计算其速度和位置,如果粒子的位置不满足边坡的约束条件,就将其舍弃。这一过程将会背离粒子群算法中趋近最优解的原理,将大多数更优解舍弃。另一种方法是给定粒子速度时就约束其满足计算边坡滑动面的约束
条件。为了保证优化算法搜索的滑动面符合上凹形的约束条件,本文提出对粒子位置进行拟合以确保符合条件。
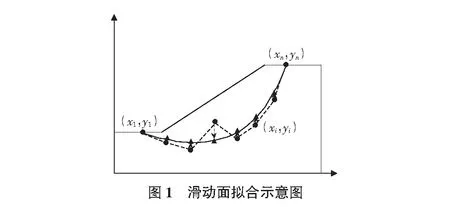
滑动面拟合示意图见图1。
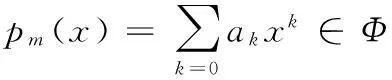
(1)
使I取最小值即为最佳拟合,当n=2时,即为本文所采用的二次拟合方法。
可以看出:
(2)
式(2)是关于a0,a1,…,am的多元函数,问题转化为求I=I(a0,a1,…,am)的极值问题。多元函数极值的必要条件为:
(3)
即:
(4)
用矩阵表示如下:
(5)
该方程组的系数矩阵是正定的,方程组具有唯一解,可以解出ak(k=0,1,…,m),则拟合多项式就是:
(6)
滑动面各点拟合的步骤如下:
1)根据(x1,y2,y3,…,yn-1,xn)求出n个滑动面点坐标。
2)列表计算:
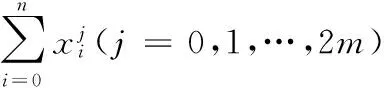
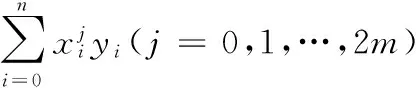
3)写出正规方程组,求出a0,a1,…,am。
在本实例中,m=2,n>m。条分段数一般大于2,取二次拟合曲线。粒子的二次拟合多项式解出后,将粒子的所有点移至拟合曲线上,如图2所示,由于二次拟合曲线在定义域上任一点具有相同的凹凸性,所以在搜索滑动面时对粒子的所有变量按照工程实际意义进行点的二次拟合,判断二次项的系数是否大于0即可。任何粒子在搜索过程中均做以上处理,可以保证所有粒子均符合约束条件而且不会破坏粒子群算法趋近最优解的趋势。得到以上可行的任意滑动面后,可以采用Bishop法计算其安全系数,将该安全系数作为目标函数代入到粒子群算法中,通过一定的运算迭代,就可以得到最终符合条件的安全系数和滑动面位置。拟合优化的粒子群算法流程图如图2所示。

将本文提出的粒子群算法运用到边坡滑动面计算的模型中,更新粒子的速度和位置时,需要首先更新粒子的x1,xn,然后更新x1和xn之间的变量。
2 算例
为了验证算法的有效性及其在边坡工程中的应用,运用提出的算法搜索边坡最危险滑裂面。粒子群参数取值如下:每次试验独立运行50次;惯性权重ω为(0.9→0.4)[5];加速因子c1i=c2f=2.5,c1f=c2i=0.5;粒子群个数N=40,即有40个初始滑动面,迭代次数T=100。
2.1无黏性边坡
针对无黏性土边坡,本文采用文献[3]的算例进行对比。图3给出了一无黏性土边坡算例,其安全系数具有解析解。
(7)
在该算例中,对比拟合优化的粒子群算法和普通粒子群算法能够发现,搜索到的滑动面均趋近于边坡倾斜面,安全系数均收敛于1。通过20次试验平均值可以发现,拟合优化后的粒子群算法比普通粒子群算法的收敛速度明显加快,普通粒子群算法所得出的收敛曲线具有两次骤降,大约需要60次迭代才能收敛于理论值,而通过拟合优化后的粒子群算法只需要不到10次迭代就可以收敛于理论值,收敛过程中只有一次骤降,其收敛速度曲线见图4。

以上结果表明,经过拟合优化后的边坡粒子群算法能够使边坡滑动面计算趋于平稳化,并能够快速收敛,使边坡滑动面的约束条件与粒子群算法的寻优趋势相结合。
2.2黏性边坡
针对黏性边坡,本文采用文献[3]的算例进行对比。边坡高度为20 m,坡角为45°。岩土体参数为:重度γ=25 kN/m3,黏聚力c=42 kPa,内摩擦角φ=17°,边坡如图5所示。
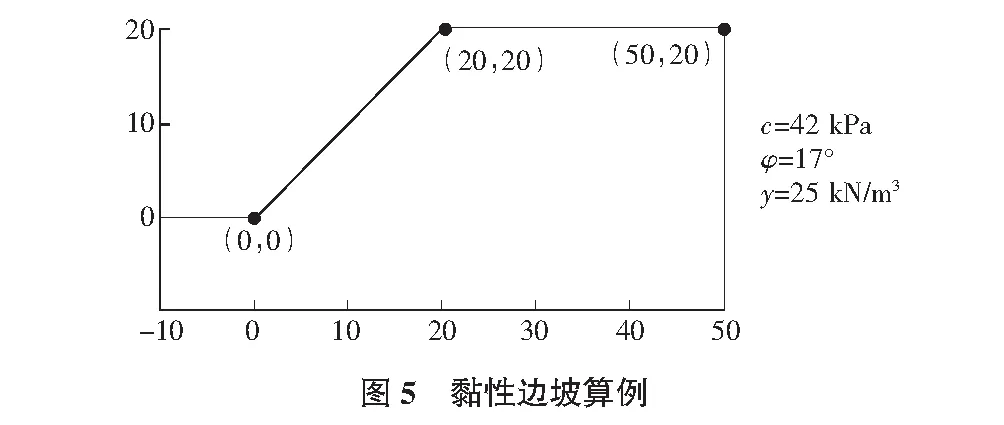

通过FLAC3D计算出该边坡结果,安全系数为1.087,通过100次迭代,普通粒子群算法计算出的安全系数为1.102,拟合修正后安全系数为1.091,边坡滑动面如图6所示。
从上述结果中可知,粒子群算法能够较为准确的计算出边坡的安全系数与最危险滑动面,经过拟合修正的粒子群算法生成的滑动面与FLAC3D计算出的滑动面更吻合,普通PSO算法生成的滑动面与FLAC3D生成的滑动面产生了交叉。
3 结论与建议
本文通过对粒子群算法在边坡滑动面计算中的应用进行研究,采用拟合优化来解决滑动面各点不满足条件的问题,得出如下结论和建议:1)通过算例一对比,拟合修正的PSO算法在计算最危险滑动面时收敛速度更快。这是因为拟合算法能够更好的保留PSO算法生成的粒子,而普通PSO算法生成的粒子往往不符合要求,大多数会舍弃。2)拟合修正的PSO算法能够保证粒子群算法的最优解趋势与满足滑动面约束条件。拟合优化保证了粒子符合现行边坡研究成果,而粒子群算法本身可以使目标函数Fs趋近于最小值。3)由于边坡滑动面进行了拟合优化,相当于人为的加入多余约束,故拟合修正的PSO算法在迭代次数比较少时只是近似解,不是最优解,理论上需要多次拟合。
[1]谢百义,陈世鸿,李名标.边坡非圆弧滑动面的PSO-GA组合搜索[J].武汉大学学报(理学版),2008,54(3):362-366.
[2]陈云敏,魏新江,李育超.边坡非圆弧临界滑动面的粒子群优化算法[J].岩石力学与工程学报,2006,25(7):1443-1449.
[3]杨善统,姜清辉,尹涛,等.边坡临界滑面搜索的改进粒子群优化算法[J].岩土工程学报,2015,37(8):1411-1417.
[4]李亮,迟世春,郑榕明,等.改进的粒子群算法及其在土坡临界滑动面搜索中的应用[J].防灾减灾工程学报,2007,27(2):153-158.
[5]Shi Y, Eberhart R. Empirical study of particle swarm optimization[A].Proceedings of the 1999 Congress on Evolutionary Computation. Washington[C].1999:1945-1950.
Feasible solution fitted modifying of Particle Swarm Optimization in slope sliding surface computation★
Shao Zhaotong
(CollegeofEnvironment&Building,ShanghaiUniversityofTechnology,Shanghai200093,China)
Through applying the fitted optimized slope sliding surface PSO, the paper calculates and analyzes safety coefficients of the slope with and without lick soil. Through FLAC3Dcalculating results comparison, the fitted modifying PSO posses enough accuracy and speed, which has certain guiding meaning for solving optimal slope sliding surface.
Particle Swarm Optimization(PSO), slope stability, sliding surface, safety coefficient
1009-6825(2016)08-0072-03
2016-01-08
邵兆通(1990- ),男,在读硕士
P642
A
★:国家自然科学基金青年基金资助项目“坡顶沉桩挤土效应及坡体变形细观机理研究”(项目编号:51208301)

