基于Midas Gen的带构架超高层建筑的动力特性研究

陈 凯 　 孔 强 　 罗军俊

(1.武汉理工大学，湖北 武汉　430000；　2.中建三局一公司，湖北 武汉　430000)



基于Midas Gen的带构架超高层建筑的动力特性研究

陈 凯1孔 强2罗军俊1

(1.武汉理工大学，湖北 武汉430000；2.中建三局一公司，湖北 武汉430000)

利用大型通用分析软件Midas/Gen，对某带构架超高层建筑的动力特性进行了研究，结果表明该类建筑在高阶振型下，顶部的构架会产生明显的高阶振动，当在某些特殊情况下，顶部构架的自振频率、下部主体的自振频率与地面振动的频率三者相差不大时，将产生共振反应，顶部附属构架会遭受严重的“鞭梢效应”。

构架，超高层建筑，鞭梢效应，模态分析

1　概述

如今，随着城市人口数量的极速攀升、城市用地面积的紧缺及成熟的施工建造工艺，使得高层建筑的数量正在不断增加，国内高层建筑的高度记录也在不断刷新。有时出于建筑立面的高度要求，在高层建筑的顶部加一个构架。但当构架的高度过高时，结构在地震作用下会产生很严重的鞭梢效应，对生命财产安全造成极大的隐患。而至今还很少有人对类似结构的动力特性进行深入研究。本文通过Midas/Gen对该类结构进行特征值分析与模态分析，以研究该类结构的动力特性，希望能对今后该类工程的设计提供一定的参考信息。

虽然对于质量与刚度分布比较均匀的结构，我们可能通过底部剪力法计算其地震作用，但是对于质量与刚度在竖向分布不均匀的结构或受高阶振型影响严重的结构，采用底部剪力法计算其地震作用可能会带来较大误差。故如需计算其地震作用，首先应当充分考虑建筑物的动力特性，为了分析建筑物的主要动力特性(基本振型、基本周期和振型参与系数)，需要对结构进行特征值分析。

每个特定的结构都有其特定的固有周期和振动形状，一般而言，不动的结构其动力特性也不尽相同。特征值分析是计算结构的固有周期和振动形状的分析方法，是进行振型分解反应谱分析和动力时程分析的基础。在Midas/Gen中，程序提供的特征值计算方法：子空间迭代法、兰佐斯法以及利兹向量法。

2　工程概况

本工程为武汉市某商业中心写字楼项目，结构体系为框架核心筒结构，建筑层数共24层，结构总高度为116.4 m，首层层高为6 m,2层层高为5.1 m,3层层高为5.7 m,4层～24层层高为3.9 m。其中±0.000 m～98.7 m为主体结构，98.7 m～116.4 m为构架附属部分(仅将结构周边竖向构件抬高)。本工程的抗震设防类别为标准设防类(丙类)，抗震设防烈度为6度，地震分组为第一组，设计基本地震加速度为0.05g。地面粗糙度类别为B类，工程建筑场地类别为Ⅱ类，抗震构造措施按照本地区抗震设防烈度的要求。结构抗震等级为框架三级，剪力墙为二级。标准层的划分为1层～3层为第一标准层,4层～14层为第二标准层，15层～24层为第三标准层，截面分别为：柱1 300×1 300,1 100×1 100,1 000×1 000,900×900；梁：400×900,350×700,250×600,200×500,200×400,150×300；剪力墙厚为350 mm,200 mm；楼板厚度为120 mm。本工程混凝土采用C30,C35,C40，钢筋全部使用HRB400。本模型的特征值分析方法为子空间迭代法，提取的振型数量为12，迭代次数为20次，收敛误差为1e-10。

2.1高阶振型

通过Midas/Gen对该工程进行模态分析，并且提取出两个高阶振型(第十一振型、第十二振型)，这两个高阶振型如图1所示。

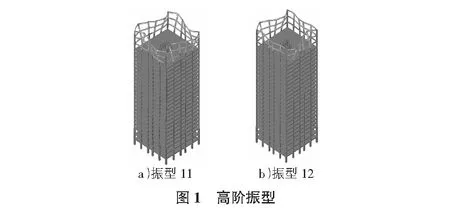
通过提取这两个高阶振型，可以发现结构的顶部附属部分的高阶振动十分剧烈。发生地震时，由于顶部附属部分的质量、刚度与下部主体结构相比相差较大，故其并不是随下部主体结构作整体振动，而是在下部主体结构的振动激励下，作二次振动。其地震响应与地面振动相比，受到了两次放大。其中，下部主体在地面振动激励下形成的地震响应为第一次放大，顶部附属部分结构在下部主体结构屋盖振动激励下形成的地震响应为第二次放大。通过这两次放大，顶部附属结构的地震响应有可能达到地面激励的数倍。当在某些特殊情况下，顶部附属部分结构的自振频率、下部主体的自振频率与地面振动的频率三者相差不大时，将产生共振反应，顶部附属部分结构会遭受严重的“鞭梢效应”。

2.2振型参与系数曲线

通过Midas/Gen对该工程进行模态分析，得出前十二阶振型的X向振型参与系数、Y向振型参与系数，并将这十二个振型参与系数连成一条曲线得到振型参与系数曲线，见图2，图3。

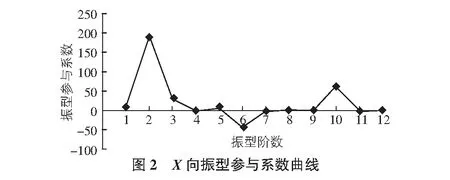
通过图2看出，当横坐标振型阶数为2时，曲线纵坐标取到极大值，表明第二阶振型为X向主振型。通过图3看出，当横坐标振型阶数为1时，曲线纵坐标取到极大值，表明第一振型为Y向主振型。通过图2，图3，还能看出该类结构的高阶振型的振型参与系数较普通结构相比偏大,当采用振型分解反应谱法计算时，应尽量多取些振型，以达到更高的计算精度。通常情况下，取6阶及以上振型即可满足要求。若取得振型数小于6，则需要适当放大附属结构的地震作用。且放大的地震作用只用于附属结构及与其直接相连的主体结构的设计，不需要向下传递。

2.3结构自振周期

通过Midas/Gen对该工程进行模态分析，得出前十二阶振型对应的自振周期，并将其整理成表1。

表1　结构自振周期

从表1可以发现随着振型阶数的提高，结构的自振周期随之变短，自振频率越来越快。结构的第一振型的周期最长，频率最低，故通常也将结构的第一振型的自振周期称为结构的基本周期。

3　结论和建议

1)该类建筑在自重荷载及风荷载作用下，一般不会发生破坏或只轻微损坏。但在地震作用下，却常遭受严重破坏。通常，顶部构架的质量、刚度远小于下部主体结构。由于在此处的质量、刚度的突变，故在地震作用下，顶部构架结构的振动由于受到下部主体结构的激励，其地震响应会放大，这时也就发生了鞭梢效应，通常我们称为二次振动。2)当采用振型分解反应谱法计算该类结构时，应尽量多取些振型，以达到更高的计算精度。通常情况下，取6阶及以上振型即可满足要求。若取得振型数小于6，则需要适当放大附属结构的地震作用。且放大的地震作用只用于附属结构及与其直接相连的主体结构的设计，不需要向下传递。当使用时程分析法计算鞭梢效应时，能够清晰地展现在地震动时，顶部塔楼或构架的振动及构件的破坏情况。采用时程分析法计算鞭梢效应较前两种具有更高的精度，故在实际工程的设计中，还需要对结构采用动力时程分析法进行最终的复核。3)在实际工程中，对该类结构设计时，应当特别注意构件主体结构与顶部构件的交界处的内力，该处的内力通常会放大2倍～3倍，故在该处的设计应当加强处理。其次，不能仅通过经验而定性地给出一个地震作用放大系数，这种方法忽略了主体结构与顶部附属部分结构的质量、刚度之间的相对关系，对于某些特殊建筑可能不适用。另外，在顶部构架的结构布置方面，可以尝试采用斜撑进行布置。

[1]张强.框架结构的鞭梢效应研究[D].太原：太原理工大学，2010.

[2]宋天军.高楼顶塔楼地震作用下的“鞭梢效应”机理及工程应用研究[D].成都：西南交通大学，2008.

[3]郭加荣.浅谈建筑结构鞭梢效应的解决方法[J].山西建筑，2008,34(25)：98-99.

[4]丁幼亮.带钢塔楼高层建筑的抗震设计方法研究[D].南京：东南大学，2003.

[5]钟万勰，林家浩.高层建筑振动的鞭梢效应[J].振动与冲击，1985,2(2)：90-96.

Study on dynamic characteristics Midas Gen high-rise building with frame-based

Chen Kai1Kong Qiang2Luo Junjun1

(1.WuhanUniversityofTechnology,Wuhan430000,China; 2.TheFirstConstructionEngineeringLimitedCompanyofChinaConstructionThirdEngineeringBureau,Wuhan430000,China)

the paper studies the dynamic characteristics of the frame-based super-high-rise building by applying large-scale analysis software Midas/Gen. Results show that: under the high-order vibration mode, the top framework will produce obvious high-order vibration. Under some special conditions, when there is no difference of self-vibration frequency of the top framework, self-vibration frequency of the lower body and ground vibration frequency, resonance reaction will occur, however, the accessory top framework will suffer from serious “whiplash effect”.

frame, super-high-rise building, whiplash effect, modal analysis

1009-6825(2016)08-0047-02

2016-01-06

陈凯(1992- )，男，在读硕士；孔强(1992- )，男；罗军俊(1991- )，男，在读硕士

TU311.3

A