基于斐波那契法的注射保压优化及脱模设计*

邹丽梅，林权

（武夷学院机电工程学院，福建武夷山 354300）

基于斐波那契法的注射保压优化及脱模设计*

邹丽梅，林权

（武夷学院机电工程学院，福建武夷山 354300）

传统单一恒定保压效果不佳，易导致塑料件产生较大翘曲变形，以汽车饰条为例，采用斐波那契迭代优化算法结合模流分析，对注射成型过程进行分段保压设计，通过8次迭代演算与数值模拟，获取了最优的保压压降组合，得到最小的翘曲变形量，比恒定保压塑料件翘曲量减少了37.55%，有效地控制了塑料件的翘曲量。实践证明该方案可靠有效。

斐波那契法；模流分析；翘曲变形；分段保压；保压优化

近几年汽车工业发展迅速，为了减少能耗减轻车重，工程塑料在汽车制造领域应用比例越来越大，尤其是车内饰件［1-4］。注射成型技术是塑料制造业中极为重要的一种加工技术，注射成型的保压阶段主要目的是补充注射模具型腔内由于冷却造成的收缩，以保障塑料件的几何形状特征，但目前单一恒定保压方式在生产中仍较普遍存在，这种方式不仅存在注射生产能源浪费等问题，而且无法有效控制成型制品的不均匀收缩，使制品发生翘曲变形［5-6］。

笔者以汽车饰条为例，基于斐波那契法，结合模流分析对注射成型过程进行分段保压优化，通过数学演化迭代调整保压阶段的关键参数，控制制品翘曲变形量，并对保压过程进行数值模拟分析验证，提出通过改变保压方式改善制品翘曲变形的方法，减少不恰当的保压对制品几何形状精度的影响，还进一步对制品脱模进行可靠设计。

1　斐波那契法的简介

意大利数学家斐波那契，提出了一个著名的“兔子数列”，该数列从第3个数起，后面的每个数都是它前面那两个数的和。如果把斐波那契数列的任何一项除以前一项，将会得到一个比值极限约为0.618，俗称黄金分割点，因此斐波纳契数列又称黄金分割数列［7-8］，用数列｛Fn｝表示，则有：

斐波那契数列在许多科技领域都得到了应用，但在注射成型技术中却较少涉及。将斐波那契数列应用于保压分段优化，可找出函数的最优值，但需要如下假设限制：（1）初始迭代时函数优化使用单峰分布描述；（2）在不确定最后迭代间距时，若迭代间距越小则越接近优化值；（3）在斐波那契法矩阵累积数值中，搜索区段是近似转化参数，由转化参数决定匹配关系。另外在保压分段优化试验前，必须选择切割点数量，在此依据试验所需要的搜寻次数，指定数列中的Fn，公式可以假设如下：

式中：W0——初始迭代，并以a≤x≤b为限制条件；

L0——搜寻范围长度；

a，b——边界范围值。

通过计算式（2），可以定义出第1阶段的搜寻范围x1和x2两个数值，如式（3），后续的切割方式类似，只是计算过程不同。

式（3）获得的x1和x2就是开始第1阶段的切割位置，并且比较这两点的合适性，开始做切割动作，如果x2的数值较差，则删除x2点到b点位置的区间，并定义出新的搜寻长度L1值，其边界范围就是从a点到x2点。新的边界定义完成后，保留原有在a点到x2点中间的切割点x1点，并通过x2-x1会得到第2组迭代数据W1，以a点加上W1后即可获得新的切割点x3，整理公式（4）：

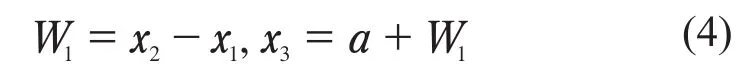
假设继续下去时要删除另一个方向，比较x3和x1后发现x3的数值不理想，因此要删除a点到x3点的区间，原理同上，此时x3点变为新的边界值，易获得第3组迭代数据W2=x1-x3，然后将x2-W2会得到新的x4点的位置，即x4=x2-W2。在此选用的数列数值越高，切割出的范围就会越接近，保压分段优化试验即是以这种方式进行研究。

根据文献［6］和文献［9］对保压曲线的研究，对恒定保压、压力逐渐提高、压力逐渐降低这3种保压方式进行了研究，获得只有压力逐渐降低的方式才能使制品产生更加均匀的体积收缩率，降低产品翘曲变形量的结论。笔者优化方向就是保压压力降低的方式，通过利用数学式来计算每一个阶段的压力降低幅度，因为注塑机的保压阶段只能设置4段，一般第1阶段的压力取值为注塑压力的80%，后3阶段才开始下降，因此以式（5）表示各阶段的压力：

式中：xi——切割点的位置；

Pn——压降幅度，单位为%。

第1段保压压力值定义为80%，且最后一段保压压力不能为0；n为压力分段段数，本试验n=4，取n=0，1，2，3所以能求得4组压力值，因为压力不能为负，所以当n=3要限制式（2）中L0的搜寻长度，令L0≤33.33。

2　创建有限元分析模型

饰件作为汽车结构的重要组成部分，不仅外表面质量要求高，而且要求装配与拆卸方便。在此选取某款家轿车内塑胶饰条为例，图1为饰条注射成型三维结构，图中1为零件，2为浇注系统，一模两腔对称布置，塑料件呈弧形细长条状，顶面要求光滑无浇注痕迹，底面均布4个卡扣用于安装连接，塑料件长500 mm，宽25 mm，厚约2.5 mm，属细条薄壳件，依经验在成型上易发生短射造成塑料件填充不完整，因此选配具有陶瓷隔热垫圈的瑞典HEATLOCK热浇道系统，热流道浇口位置的设定直接关系到熔体在模具型腔内的流动［10］，从而影响聚合物分子的取向和制品成型后的收缩和翘曲，由于该塑料件为细长条状，为了得到合理的充填效果宜采用多点进料，依据塑料件制品的特性与需求，在此采用两点香蕉型潜伏浇口底面进料方式。

图1　饰条注射成型三维结构

创建有限元模型是进行塑料件模流分析的重要前提，而网格划分又是建立有限元模型的关键［11］。笔者将UGNX8.0建好的饰条三维模型先进行必要的简化处理，删除饰条顶面上过渡小圆角和底面部分加强筋，再导人Hypermesh进行有限元网格的划分，利用 Hypermesh 的中面抽取功能对饰条模型进行几何清理和修复，进一步清除不必要的细节，为高质量的网格划分奠定基础［12］，然后使用 2D 网格划分功能进行网格划分并导出.udm格式文件，最后导人MoldFlow 中。在Moldflow Plastics Insight（MPI）中，根据图1饰条注射成型三维结构创建热流道浇注系统，另依据注塑模具冷却设计原则，在动定模型腔板上分别布置冷却管道，最终创建的塑料件有限元分析模型如图2所示。

图2　饰条有限元分析模型

由于塑料件细条弧状特征，无论是定模还是动模冷却管道设计都要求不等高，整体式的定模型腔采用左右两条直流循环式回路，组合式的动模镶件设计各自独立的冷却回路，两个型腔左右两侧共计4条。

3　模流初分析

饰条材料选用奇美公司生产的牌号为POLYLAC PA-747的丙烯腈-丁二烯-苯乙烯塑料（ABS），依据经验设置成型工艺参数：熔体温度230℃，模具表面温度50℃，顶出温度85℃，最大许可剪切应力0.28 MPa， MoldFlow2012中的分析类型为冷却+流动+翘曲。通过模流初分析获知饰条注塑压力值为48.35 MPa，注射时间为2.10 s，末端冷却凝固时间约为8.10 s，近浇口塑料件冷却凝固时间为20.10 s，保压压力取值为注塑压力的80%，保压时间18.00 s。图3为饰条模流分析翘曲变形云图。从图3可以看出，饰条两端的翘曲变形量较大，最大值为0.674 2 mm，两点浇口附近的翘曲变形量最小约0.05 mm，总体上看饰条变形量大且变形量分布不均，对制品的几何形状精度及装配质量都有显著影响。

图3　恒定保压饰条翘曲变形（放大20倍）

笔者仅对保压压力及时间进行调整，所以将其它几个关键的试验工作参数设置为定值，现将试验保压分为两个部分，第一部分设定为恒压，保压压力取值为注塑压力的80%，时间为2.10～8.10 s；第2部分设定为3段阶梯式降压，时间为8.10～20.10 s，各阶段分配时间为8.10～12.10 s，12.10～16.10 s，16.10～20.10 s，在此以饰条整体翘曲度为指标，通过斐波那契优化方法，寻找一组最理想的压降数值。

4　基于斐波那契法进行保压优化

已知注塑机压力分段数为4，试验目标为求出9个切割点xi，所以取斐波那契数列第10项开始优化计算， 根据数列取Fn=89，Fn-2=34，L0=0～33.33代人公式（2）可以得到 W0=12.73，通过公式（3）可以求出第1次迭代的x1=12.73，以及x2=20.60。

再将x1和x2分别代人公式（5）求出两组压力组合值：

Px1=80.00%，70.06%，60.14%，50.12%

Px2=80.00%，63.93%，47.87%，31.80%

然后将百分数转化为压力值，如下式：

P′x1=38.68，33.87，29.08，24.28 MPa

将两组数据代人模流分析，进行翘曲变形分析并比较结果。图4为切割点x1的翘曲变形云图。从图中可以获知饰条最大变形量为y1=0.584 3 mm；图5为切割点x2的翘曲变形云图，从图中可以获知饰条最大变形量为y2=0.508 0 mm。

图4　切割点x1饰条翘曲变形（放大20倍）

图5　切割点x2饰条翘曲变形（放大20倍）

比较x1和x2两切割点的翘曲变形量值，x2点优于x1点获得更小的翘曲变形量，所以将x2点到边界33.33区间删除，将x2点设置为新边界，并重新计算获取新的切割点x3，以及计算出该切割点的压力值，根据公式（3）与（4），可得x3=7.87。

继续代人公式（5）计算压降幅度：

Px3=80.00%，73.86%，67.73%，61.60%

转化压力数值：

P′x3=38.68，35.72，32.15，29.78 MPa

再将数据代人模流分析，获得饰条翘曲变形量为y3=0.4786 mm，显然x3点优于x2点获得更小的翘曲变形量，所以将x3点设定为新的边界，并重新计算获取新的切割点x4，以及计算出该切割点的压力值，然后代人模流分析获取切割点x4的翘曲变形量，再与保留的切割点x3进行比较取舍。以此类推重复计算，共进行了8次迭代，第8次优化迭代计算结果如下：

综上结果，准确提取概念关键信息，并能运用已有认知结构抽象概念的内涵，是创设型概念理解的关键。针对上述存在的问题，作出以下教学建议。

P′x9=38.68，36.28，33.88，31.48 MPa，y9=0.4210 mm；

P′x7=38.68，36.14，33.59，31.05 MPa，y9=0.4220 mm

经过8次演算迭代，此时饰条最大翘曲变形量接近0.42 mm，图6为优化后饰条翘曲变形云图。图中浇口处的最小变形量约0.04 mm，与第7次迭代时相比较变化量已经不大，变化幅度仅为0.001 mm，到此就不需要再继续切割了，如果继续切割可能造成前后彼此重叠，所以演算结果已经符合收敛位置要求，因此饰条分段保压数值分别是：第1阶段38.68 MPa、第2阶段36.28 MPa、第3阶段33.88 MPa、第4阶段31.48 MPa，控制的翘曲变形量最为理想。从8次演算迭代结果可以看出并不是保压压降幅度大或者小，就可以正确地控制制品翘曲变形量，这是由于模具型腔内的变化并非单纯只有压力的流动，也包含其它影响因素。

图6　优化后饰条翘曲变形（放大20倍）

5　饰条脱模设计

饰条为细条薄壁弧状塑料件，注塑中脱模的设计也非常重要，脱模力不平衡、顶出位置设置不当、顶出零件运动不顺畅都很容易导致产品翘曲变形［13］，因此如何完整可靠地将饰条脱离型芯是脱模设计的关键。从图6可以获知饰条翘曲变形量分布情况如下：两端较大、浇口附近比较小、中间部分次之，所以最好在这3个区域同时设置顶出零件，浇口附近可以稍多，可以承受稍大的脱模力。从图2可以看出，饰条底部含有4个卡扣和两个支撑柱，卡扣筋板又小又薄，这些小结构在制品的成型收缩时容易与模具发生粘合现象，造成脱模困难；而且饰条卡扣上勾配面设置有凸缘，如果设计普通侧抽机构进行脱模必然导致模具结构复杂，在此采用脱模与侧抽一体化设计，卡扣使用独立的方形斜顶与模具型芯配合形成一个封闭的型腔来成型，方形斜顶底部与模具推杆固定板上的滑块相接传动动力与运动，如此不仅卡扣不会产生镶拼线，而且能使脱模机构运动自如，从而降低模具制造成本，饰条脱模机构设计如图7所示。图中1为成型卡扣的方形斜顶，通过注塑机顶杆推动固定在推杆固定板上的滑块7，并在支撑块5的导路中将饰条2脱离型芯，4个卡扣分别由4个方形斜顶进行侧抽与脱模，滑块7与支撑块5保证了斜顶的运动可靠，饰条上的2个十字支撑柱由十字镶件4成型，脱模依靠固定在推杆固定板上的推杆6进行，推杆6的设计符合翘曲变形量大小分布，在浇口附近设计推杆有3根，饰条两端与中部分别单独设计1根，4个斜顶1介于9根推杆6之间，整体上使脱模力平衡，顶出位置分布合理，图中3为瑞典HEATLOCK热浇道系统。经生产实践证明该脱模系统运作可靠，很好地维持了制品的几何形状精度。

图7　饰条脱模设计

6　结语

注射保压阶段的主要目的是为了补足模具型腔内因冷却造成的收缩，以维持塑料件的几何形状，但是传统单一恒定保压效果不佳，不仅存在能源浪费，而且易导致塑料件产生较大的翘曲变形。以汽车饰条为例，通过模流分析获取塑料件末端冷却凝固时间点与近浇口塑料件冷却凝固时间点，采用迭代优化算法结合模流分析进行分段保压设计，在两个重要时间内做压力调降。

在此首先使用斐波那契法迭代演算取得保压阶段压力值，再导人Moldflow中进行翘曲分析，获取各次迭代的翘曲变形量，最后找出最佳的压力降的组合以及压力值。通过比较恒定保压与优化后的分段保压，饰条的最大变形量由0.6742 mm下降到0.4210 mm，下降幅度达到37.55%，浇口附近的最小翘曲量也有进一步下降，总体上塑料件变形幅度得到很好的改善，有效地控制了塑料件的翘曲量。另外通过实践证明该方法可靠有效，该优化方法不但可以应用于其它注射参数的选取，也给研究注射成型与模具设计的相关学者提供一定参考。

［1］ 林建兵.汽车内饰件注塑成型数值模拟及缺陷分析［J］.制造业自动化，2015，37（7）：106-108. Lin Jianbing. The car inner decoration molding numerical simulation and the analysis of defects［J］. Manufacturing Automation，2015，37（7）：106-108.

［2］ 赵龙志，赵明娟，宋金良.汽车内饰件下装饰盖注塑模具设计［J］.塑料工业，2007，35（10）：32-34. Zhao Longzhi，Zhao Mingjuan，Song Jinliang. Design of injection mold for nether decoration lid of automobile inner decoration［J］. China Plastics Industry，2007，35（10）：32-34.

［3］ Chen Shia-Chung，Jong Wen-Ren，Chang Jen-an.Dynamic mold surface temperature control using induction heating and surface appearance of weld line［J］.Journal of Applied Polymer Science，2006，101（2）：1 174-1 180.

［4］ 韩宝菊.基于Moldflow 优化分析的轿车内饰出风口面板注塑模设计［J］.塑料工业，2016，44（5）：48-53. Han Baoju. Optimization of injection mold design for a panel vent based on Moldflow［J］. China Plastics Industry，2016，44（5）：48-53.

［5］ 张德强，张琰，孟小鑫，等. 基于 Moldflow 的保压曲线优化方法研究［J］.辽宁工业大学学报：自然科学版，2015，35（1）：37-40. Zhang Deqiang， Zhang Yan， Meng Xiaoxin， et al. Packing curve optimization methods based on Moldflow［J］. Journal of Liaoning University of Technology：Natural Science Edition，2015，35（1）：37-40.

［6］ 张宇，刘恩，陈弦.基于MOLDFLOW保压曲线优化设计在托盘中的应用［J］.塑料工业，2011，39（2）：41-44. Zhang Yu， Liu En，Chen Xian. The application of packing prosiles optimization design of moldflow in plastic plate［J］. China Plastics Industry，2011，39（2）：41-44.

［7］ 闫萍，王见勇.斐波那契数列与黄金分割数［J］.高等数学研究，2005，8（1）：28-31. Yan Ping，Wang Jianyong. Fibonacci sequence and golden section number［J］. Studies in College Mathematics，2005，8（1）：28-31.

［8］ 佘守宪，胡颉.黄金数与Fibonacci数列［J］.物理与工程，2006，16（2）：1-8. She Shouxian， Hu Jie. Golden number and Fibonacci sequence［J］. Physics and Engineering，2006，16（2）：1-8.

［9］ 陶永亮.注塑保压切换方式选择［J］.塑料制造，2012（4）：72-76. Tao Yongliang. Injection to keep the pressure switch mode option［J］. Plastics Manufacture，2012（4）：72-76.

［10］ Spina R.Injection moulding of automotive components： Comparison between hot runner systems for a case study［J］. Journal of Mate rials Processing Technology，2004，155：1 497-1 504.

［11］ 林权.含锥螺纹分段螺纹的双头螺纹转接头注塑模设计［J］.工程塑料应用，2015，43（4）：62-67. Lin Quan. Injection mold design of double threaded connector with both taper thread and segmented thread［J］. Engineering Plastics Application，2015，43（4）：62-67.

［12］ 边弘晔，李鹤，闻邦椿.HyperMesh有限元前处理关键技术研究［J］.机床与液压，2008，36（4）：160-164. Bian Hongye，Li He，Wen Bangchun. Study on the key techniques of finite element preprocessing base on HyperMesh［J］. Machine Tool & Hydraulics，2008，36（4）：160-164.

［13］ 林权.基于MPI汽车内装饰板注塑模优化设计［J］.井冈山大学学报：自然科学版，2011（2）：83-86. Lin Quan. MPI-based optimization design of injection molds for automotive trim［J］. Journal of Jinggangshan University：Natural Science Edition，2011（2）： 83-86.

Optimization of Injection Holding Process and Demoulding Design Based on Fibonacci Method

Zou Limei， Lin Quan
（School of Mechanical and Electrical Engineering， Wuyi University， Wuyishan 354300， China）

The traditional single constant pressure-holding result is ineffective， which cause relatively large distortion. Taking automotive trims as examples， adopting fibonacci iterative optimization algorithm and mold flow analysis. The design of section pressure holding to injection molding processes was conducted. Through eight times of iterative calculation and numerical simulation，optimal pressure holding and drop combination as well as minimum deformation are obtained， which decreases 37.55% compared with the deformation of relative constant pressure holding molding， which effectively control the deformation of mold parts. Practice approves that this program is effective and reliable.

fibonacci method； mold flow analysis； deformation； section pressure holding； pressure holding optimization

TQ320

A

1001-3539（2016）10-0057-05

10.3969/j.issn.1001-3539.2016.10.012

*福建省教育厅A类科技项目（JA13323），南平市科技计划基金项目（N2013X01-7）

联系人：邹丽梅，讲师，硕士，从事机械电子工程研究

2016-07-13