轨迹生成四杆机构优化及仿真研究

杨 帆

(武汉科技大学城市学院 机电工程学部，武汉 430083)



轨迹生成四杆机构优化及仿真研究

杨 帆

(武汉科技大学城市学院 机电工程学部，武汉 430083)

由于轨迹生成四杆机构存在横向及纵向误差较大，精度较低等问题，因此其不能很好满足四杆机构运动轨迹的要求。对此，文章分析了四杆机构几何参数，采用修正误差函数法，构造优化目标函数。通过具体实例对四杆机构运动的相关尺寸进行优化，借助Matlab软件计算得出四杆机构最佳几何尺寸值。将优化结果进行仿真，并且与传统方法进行对比。仿真结果显示，四杆机构横向及纵向误差较小，效果较好。采用修正误差函数法对轨迹生成四杆机构优化，优化后四杆机构运动轨迹精确度较高，能够满足多种四杆机构输出运动的要求。

四杆机构；修正误差函数；优化；仿真

0 引言

随着国内自动化产业的快速发展，机构的应用也越来越广泛。国内常见的机构主要包括：凸轮机构、齿轮机构、带轮机构、连杆机构等。在众多机构中，连杆机构的应用领域相对广泛，主要应用在工程机械、农业机械、折叠伞、太阳能板、机械手、人造卫星及人体假肢等。而连杆机构主要包括四杆机构、五杆机构、六杆机构及八杆机构等。四杆机构是其它多杆机构的重要组成部分，研究人员要想设计出多杆机构，必须熟悉四杆机构的基本原理和设计方法。因此，四杆机构研究具有重要的意义。

当前，对轨迹生成机构的研究方法有多种。例如：文献[1-3]针对步行机器人路径规划与控制问题展开了研究，采用非线性曲线构建人体关节各个转角运动变化的模型，进而对模型进行了仿真和分析。文献[4-6]针对轨迹生成连杆机构方法及可视化问题展开课研究，生成了很多曲线拟合点，采用三次非均匀 B 样条曲线进行拟合。文献[7-9]针对常用的混合驱动机构轨迹综合问题展开了研究，研究了混合驱动机构运动过程的轨迹综合方法及相关理论。以往研究轨迹生成机构的综合误差较大，很难适应快速发展的市场需要。对此，本文采用了修正的距离误差函数，结合具体实例优化四杆机构，对优化产生的相关变量参数值输入到Matlab软件中进行误差仿真。同时，与以往研究成果进行对比。对比结果表明，横向及纵向误差降低，采取修正的距离误差函数方法较好，为以后四杆机构优化的研究提供了参考。

1 四杆轨迹生成机构

轨迹生成四杆机构OaABOb如图1所示。C是连接点，θ1是由机架和X轴产生的角度，θ2是输入角，r1、r2、r3及r4分别是机架、输入杆、连接杆和输出杆的长度，r5和r6是连接点C的局部坐标。θ3是连杆AB和机架OaOb之间构造的角度。X0和Y0是Oa的坐标。

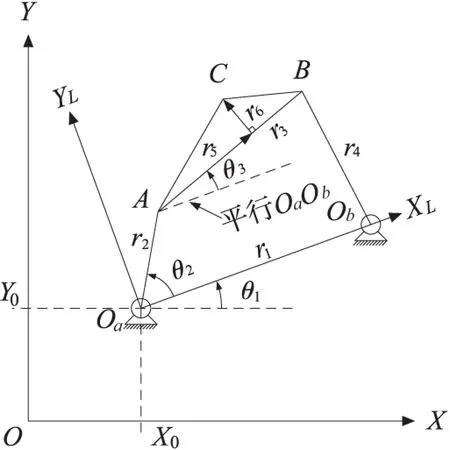
图1 轨迹生成四杆机构的设计变量

由对连杆点的位置分析可得如下关系式：

(1)

式中：XL和YL是C在机架Oa-XLYL中的坐标。

四杆机构的轨迹产生通常有两种，分别为有指定时间的轨迹生成和无指定时间的轨迹生成。

有指定时间的轨迹生成的矢量如下：

无指定时间的轨迹生成的矢量如下：

2 目标函数的构造

2.1 基于欧几里得距离误差的误差函数

误差函数是用于确定指定轨迹点和产生轨迹点之间的位置误差数量的目标函数的一部分。在轨迹生成机构的综合中，使用最多的误差函数是“欧几里得距离误差累积平方[10]”。这个误差函数，我们表示为CSDE，如公式(2)所示。

(2)

式中：(xi，yi)是第i个指定的轨迹点，(xgi，ygi)是第i个产生轨迹点，n是指定轨迹点的数量。

2.2 修正的误差函数

当在一定时间内出现的误差保持在合理范围内时，这样的需求将意味着产生的连接点应该尽量接近指定的轨迹点。对所关心的在一点上指定轨迹的趋势而言，我们可以定义一个“纵向”方向(沿着切线方向接近在该点的轨迹)和一个“横向”方向(与纵向方向正交)。对“横向误差”(也就是欧几里得距离误差中沿着横向方向的部分)要求更高，对“纵向误差”(也就是欧几里得距离误差中沿着纵向方向的部分)方向上的误差要求更宽。这通过设置一个对横向误差的加权比F>1.0来实现。这样做有望推动产生的连杆点接近指定的轨迹，尽管在接近的过程中可能会存在一个增加的误差。指定的点和指定的轨迹如图2所示。以n为数量的通过(xi，yi)，i= 1, 2,…,n，定义的指定轨迹点的坐标也在图2中展示。

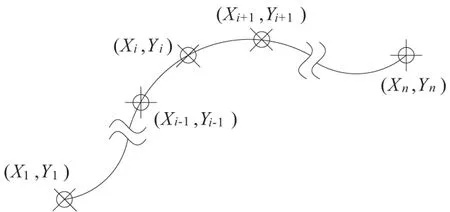
图2 指定的轨迹和轨迹点

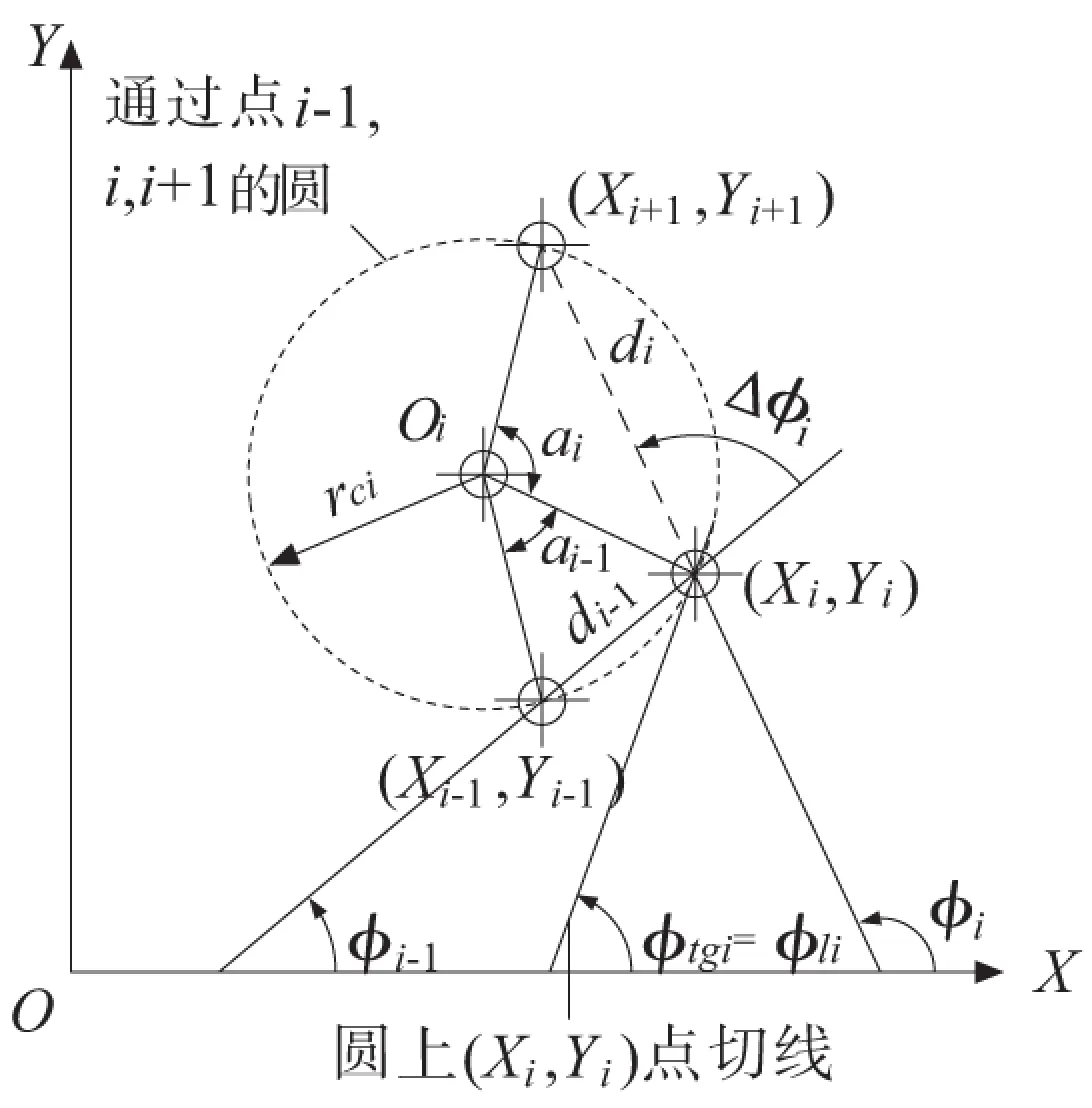
图3 中间指定轨迹点上的纵向方向

图3展示了三个相邻的指定轨迹点，编号为i-1、i和i+1，由连接相邻的指定点(xi，yi)和(xi+1，yi+1)的线段与X轴定义的角度φi由下式给出。

(3)

式中：Si=yi+1-yi，Ci=xi+1-xi，Atan2是2倍幅角的反正切函数，它能返回在正确象限内的角度值，该值取决于幅角符号的正负。点(xi，yi)和(xi+1，yi+1)之间的距离表示为di，如下所示。

(4)

将φtgi用表达式代替，并注意到φli=φtgi，我们可以得到如下的关于角度φli的表达式。

(5)

因为点1之前没有点，公式(5)不能直接使用。要估算其值需要知道φ0、l1和Δφ1的值。图4展示了指定的轨迹点1、2和3，以及通过它们的圆。连接点1-2和点2-3的弦长分别是d1和d2，它们在圆心分别得到角度α1和α2。从图4上可以观察到α1≈(d1/rc2)和α2≈(d2/rc2)，rc2是通过点1、2和3的圆的半径。它满足条件α2=(d2/d1)α1=l2α1。为了能将公式(5)应用于点1，我们选择了一个假想的编号为0的点。该点将被做为点1之前的点，该点位于一个圆上。该圆以0-1弦的长度等于1-2弦的长度的方式通过点1、2和3。我们假定点0位于通过点1、2和3的圆上(这等于假设在点0和点1之间的轨迹的延长段的曲率和位于点1和点3之间的轨迹的曲率相同)，且d0=d1。对d0=d1的假设主要是为了简化分析。注意到Δφ2=(α1+α2)/2=(α1+l2α1)/2=(1+l2)α1/2和Δφ1=α1，我们得到Δφ1=2Δφ2/(1+l2)=2(φ2-φ1)/(1+l2)。从Δφi的定义，我们得到φ0=φ1-Δφ1。这里φ1和φ2，是由弦1-2和弦2-3分别与X轴得到的角度。将这些关于和的表达式代入公式(5)中，注意到l1=(d1/d0)=1，可以得到如下的关于φl1的表达式。

(6)

图5展示了指定的轨迹点n-2、n-1和n，此圆具有和rc,n-1相等的半径。其它细节和图4相似，可以得到以下关于φln的表达式。

(7)

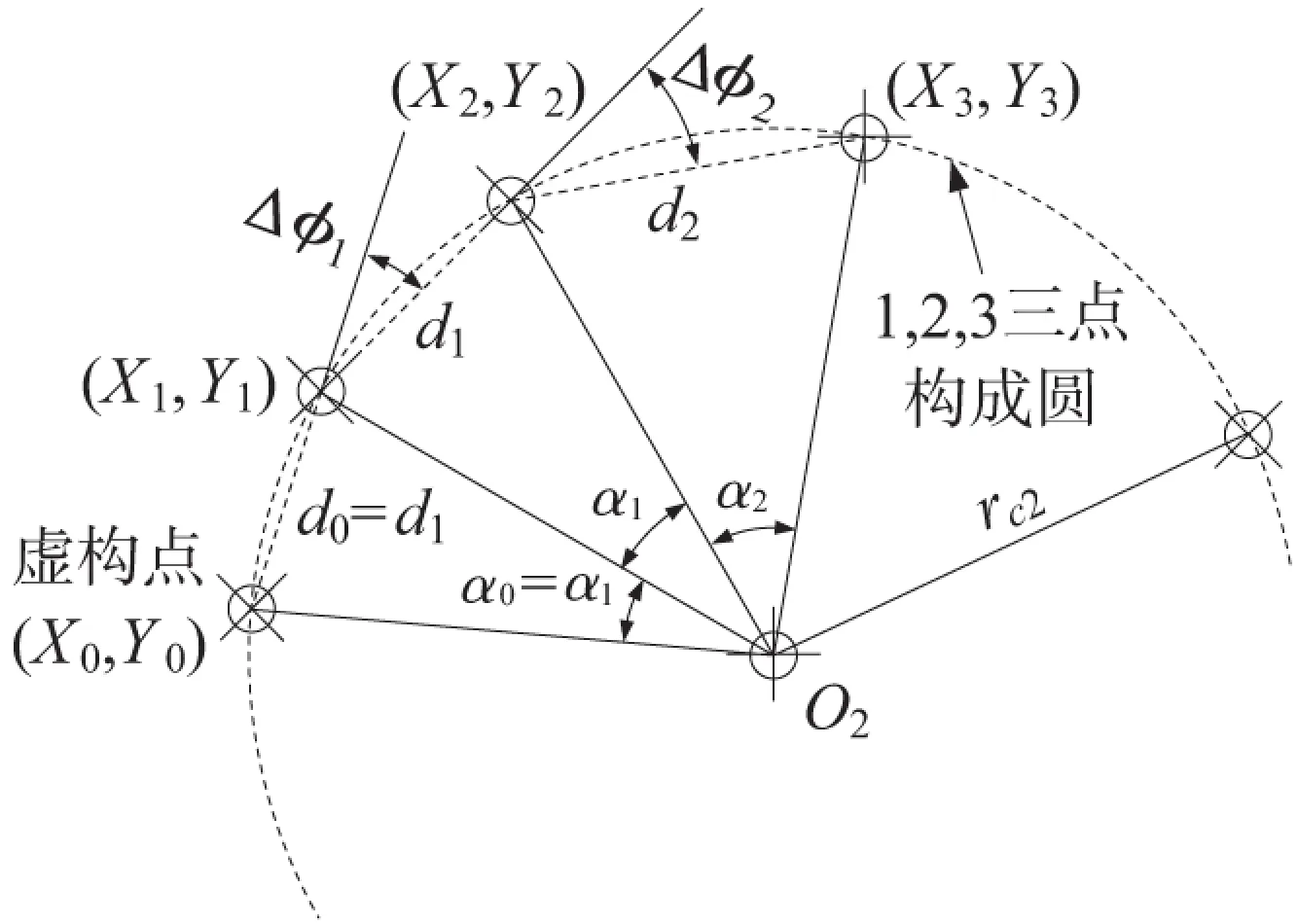
图4 第一个指定轨迹点的纵向方向

图5 最后指定轨迹点的纵向方向

定义了在点(xi，yi)的纵向和它的依照由公式5～公式7给出的角φli的方向。在指定点(xi，yi)的横向方向也即定义了，也就是在同一点沿着对纵向方向逆时针方向90°，如图6所示。在点(xi，yi)的横向方向和x轴得到了角度φti，该角度由下式给出。

φti=φli+π/2

(8)

公式5～公式8被用来求在每一个指定的轨迹点上由纵向方向和横向方向得到的角度值。在优化过程中，每一种候选机构都被评估，评估方法是，在每一点i上，沿着纵向和横向方向，计算欧几里得距离误差矢量(从指定轨迹点到对应的生成的轨迹点的矢量)中各部分的绝对值。沿着纵向和横向方向的，对应于第i个指定点的，欧几里得距离误差矢量组成的绝对值，被分别标记为el,i和et,i。关于el,i和et,i的表达式在随后的解释中求得。

图6 最后指定轨迹点的纵向方向

来自于指定的轨迹点Pi(xi，yi)和生成的轨迹点Pgi(xgi，ygi)的向量用PiPgi表示。它表示对应于指定的点Pi，欧几里得距离误差矢量，给出其表达式为PiPgi=(xgi-xi，ygi-yi)。沿着纵向和横向方向的单元矢量分别是u1=(cosφli，sinφli)和ut=(cosφti，sinφti)。误差矢量PiPgi沿着纵向方向的投影将等于点积(PiPgi·u1)=(xgi-xi)cosφli+(ygi-yi)sinφli。现在纵向误差el,i，被定义为误差矢量PiPgi沿着纵向方向的投影的绝对值，因此它由下式给出。

(9)

类似地，误差矢量PiPgi沿着横向方向的投影，将等于点积(PiPgi·ut)=(xgi-xi)cosφti+(ygi-yi)sinφti。横向误差et,i被定义为误差矢量PiPgi沿着横向方向的投影的绝对值，且由下式给出。

(10)

现在，在点i修正的距离误差，被标记为emi，它的定义为：

emi=Feti+eli

(11)

式中：F是在纵向和横向误差之间的“等价因数”。

在第i个指定的点处，CMDE函数相等的修正距离误差曲线(直线)，如图7所示。因此，所有生成的位于虚线平行四边形上的点，都被认为有一个相等的修正误差值em。应该注意到对F=1.0来说，该相等的修正距离误差曲线(直线)将组成一个正方形，该正方形的对角线沿着纵向和横向方向，每一条对角线的长度是修正的距离误差的两倍。另一方面，对CSDE来说，相等的距离误差曲线将是圆，以指定的点(xi，yi)为圆心的圆。这将带来一个结果，那就是F=1.0的CMDE函数和CSDE不相同。

图7 CMDE函数的均差线

基于此修正距离误差的定义，该累积的修正距离误差函数(CMDE)可以被定义为：

(12)

2.3 约束条件

在本文中，约束条件包含以下几个部分：①要综合的四杆机构必须是曲柄摇杆机构；②最长杆杆长和最短杆杆长之比必须少于或等于一个指定的数值；③从90°开始的传动角偏差必须少于或等于一个指定的数值；④设计变量必须位于指定的范围内，杆长必须是正值。这些约束条件通过如下的方法执行：

约束条件1：为了保证综合机构是一个曲柄摇杆，一个机构需要满足两个子约束(a和b)。这通过对优化过程中产生的每一个机构执行以下的步骤来保证。

①四杆的长度(机架长度r1，输入杆长度r2，连杆长度r3，输出杆长度r4)需要被排序以找出最短的杆长(s)，最长的杆长(l)和中间的杆长。然后，需要检查以下的条件是否满足。

s+l≤p+q

如果以上的条件不满足，一个补偿量M1a需要增加到目标函数值中，因为这样的机构不是一个非格拉霍夫机构。

②检查最短的具有长度s的连杆是否为输入杆。如果不是，一个补偿M1b需要添加到目标函数中，因为这样的机构可能不是曲柄摇杆机构。

约束条件2:计算最长杆和最短杆的杆长比(l/s)并检查它是否小于或等于指定的数。如果没有，需要在目标函数中增加一个补偿M2。

约束条件3：对一个四杆机构，传动角γ是在连接点的，连杆的速度差矢量方向和输出杆绝对速度的方向的夹角。从运动传递的有效性和对输出杆的力来看，需要让传动角的值最少从90°开始偏离。可以直接地看到，对一个四杆机构，其传动角的最大值和最小值可以由以下的公式给出。

(13)

这个约束条件包含在公式推导中，即首先通过使用以上给出的公式计算传动角的最大值和最小值，然后检查它们从90°开始的偏差是否少于或等于一个指定的数。如果没有，增加一个补偿量M3给目标函数。

约束条件4：在总体的初始化过程中指定一系列设计变量。只要任何一个设计变量的值超出了指定的范围一点点，就对该范围的下限值和或上限值进行重置，不管是哪一个接近现有的变量值。通过指定一个非负的数做为它们中每一个的下限值，可保证杆长总是会保持正数。没有补偿与该限制条件关联，因为它是通过差分进化算法[11]自身实现的。

2.4 目标函数

目标函数即关于设计变量的，必须要最小化得到最佳机构的函数。它也需要关心约束条件。目标函数fobj给出如下：

(14)

式中：Ef(X)是在2.1节和2.2节(CSDE和CMDE)中讨论的两个误差函数中的任何一个，M1a、M1b、M2和M3是违反各条约束后添加到目标函数的补偿。h1a(X)、h1b(X)、h2(X)和h3(X)是设计变量矢量的函数。当X违反相应的约束时，式中的X值为1；当X满足相应的约束，式中的X值等于0。现在优化问题可以形成如下：最小化的fobj满足xi∈[lli,uli]∀xi∈X，式中X是设计变量的矢量，lli和uli是对不同的xi指定的下限和上限值。

3 设计实例

由公式(11)可知，F的取值有多种，本文以F=3.0为例，通过Matlab软件研究横向和纵向误差变化情况。通过Matlab软件对相关约束尺寸进行计算，最佳机构变量相关参数如表1所示。

表1 最佳机构变量相关参数

在本文中，研究结果是采用n=13，在13个指定的轨迹点中的每一点处，对所关心的误差(横向的/纵向的)进行了计算及求和，以得到总体的(横向的/纵向的)误差。对13个指定的轨迹点，横向和纵向方向如图8所示。同时，采用CMDE误差函数等价因子F=3.0，最佳机构及产生的轨迹如图9所示。

将最佳机构变量的相关参数值CSDE和CMDE输入到Matlab软件中进行仿真，横向误差仿真结果如图10所示，纵向误差仿真结果如图11所示。仿真结果数据如表2所示。

图8 13个指定的轨迹点 图9 最佳机构及产生的轨迹

图10 横向误差

图11 纵向误差

参数CSDE(F=3.0)CMDE(F=3.0)单位横向误差0.110.08cm纵向误差0.170.12cm

从表2可知，在F=3.0时，CSDE仿真结果的横向误差最大为0.11cm，而CMDE仿真结果的横向误差最大为0.08cm，横向误差大约下降27.3%；CSDE仿真结果的纵向误差最大为0.17cm，而CMDE仿真结果的纵向误差最大为0.12cm，纵向误差大约降低了29.4%。对目标函数约束后，总体产生的误差明显降低。

4 结束语

本文采用了修正误差函数法研究了轨迹生成四杆机构的优化问题，主要是通过修正距离误差函数结合具体给出的实例进行说明。对实例的相关变量参数进行仿真验证，与传统研究的欧几里得距离误差函数进行比较。优化后仿真结果显示，采用修正距离误差函数优化效果良好，横向和纵向误差大幅度的降低，横向

误差相对以往研究成果降低27.3%，纵向误差相对以往研究成果降低29.4%，优化后误差降低效果得到了很大的改善，为以后四杆机构优化的深入研究提供了参考价值。

[1] Yannick Aoustin,Arnaud Hamon. Human like trajectory generation for a biped robot with a four-bar linkage for the knees[J].Robotics and Autonomous Systems,2013,61 (12):1717-1725.

[2] Prasad Vilas Chanekar,Michael Angelo Amith Fenelonb, Ashitava Ghosal. Synthesis of adjustable spherical four-link mechanisms for approximate multi-path generation [J].Mechanism and Machine Theory,2013,69(11):540-550.

[3] Yong Ma,Hongwei Wang,Yong Xie,etal. Path planning for multiple mobile robots under double-warehouse[J]. Information Sciences, 2014,278(10):360-375.

[4] 赵彦微.平面四杆机构轨迹综合方法及可视化表达[D].哈尔滨:哈尔滨工业大学,2014.

[5] Shaoping Bai,Jorge Angeles. Coupler-curve synthesis of four-bar linkages via a novel formulation[J].Mechanism and Machine Theory,2015,94(12):178-186.

[6] Biswanath Panda, Ashish Dutta.Design of a partially compliant crank rocker mechanism using Ionic Polymer Metal Composite for path generation[J].Materials and Design,2012, 31(10):2471-2477.

[7] 何东.一种新的动态轨迹综合方法的研究[D].沈阳:东北大学,2012.

[8] I Hermadi,C Lokanb,R Sarker. Dynamic stopping criteria for search-based test data generation for path testing[J]. Information and Software Technology,2014,56(12):397-406.

[9] Jinn-Biau Sheu,Sheng-Lun Hu,Jyh-Jone Lee. Kinematic synthesis of a four-link mechanism with rolling contacts for motion and function generation[J].Mathematical and Computer Modelling,2013, 48(3):806-816.

[10] Simon Perreault,Philippe Cardoua,Clément Gosselin.App-roximate static balancing of a planar parallel cable driven mechanism based on four-bar linkages and springs[J]. Mechanism and Machine Theory,2014,79 (10):68-78.

[11] Otto Röschel.Overconstrained mechanisms based on planar four-bar-mechanisms[J].Computer Aided Geometr-ic design,2014,31(10):595-601.

(编辑 李秀敏)

Optimization and Simulation Study of Path Generating Four-bar Mechanisms

YANG Fan

(Mechanical and Electrical Engineering Department ,City College,Wuhan University of Science and Technology, Wuhan 430083,China)

Because horizontal and vertical error is considerably large of path generating four-bar mechanisms,precision is relatively low,which can't well meet the requirements of four-bar mechanisms trajectory.To this,the geometrical parameters of four-bar mechanisms are analyzed in this paper.Take correction method of error function, the objective function of optimization is constructed.Relevant dimensions of four-bar mechanisms motion is optimized through specific examples,best of four-bar mechanisms geometry size values were calculated with the help of Matlab software. The results of the optimization is simulated,and compared with the traditional method.The simulation results show that the horizontal and vertical error of four-bar mechanisms is smaller, effect is good. Optimization of path generating four-bar mechanisms by the method of correction error function, after optimization of four-bar linkage trajectory track accuracy is higher, which can meet the requirements of a variety of output motion of four-bar mechanisms.

four-bar mechanisms; correction error function;optimization; simulation

1001-2265(2016)10-0035-05

10.13462/j.cnki.mmtamt.2016.10.010

2015-11-12；

2015-12-08

杨帆(1976—)，男，武汉人，武汉科技大学城市学院讲师，硕士，研究方向为机械设计理论和运动仿真，(E-mail)yangfan201511@sina.com。

TH112;TG506

A