基于GA-GRNN的复合铣床立柱优化*

高亚洲，史耀耀

(西北工业大学 现代设计与集成制造技术教育部重点实验室，西安 710072)



基于GA-GRNN的复合铣床立柱优化*

高亚洲，史耀耀

(西北工业大学 现代设计与集成制造技术教育部重点实验室，西安 710072)

立柱是复合铣床的主要承力部件，其质量直接影响机床的刚性和动态性能，进而影响加工质量，因此对有必要对复合铣床立柱质量进行优化设计。首先采用灵敏度分析法，获得影响立柱质量的敏感尺寸参数；其次基于均匀试验和GRNN神经网络分别建立立柱质量、前2阶固有频率和最大变形量的模型，并通过遗传算法对模型方程进行寻优求解，得出尺寸参数最优解组合；最后在优化后立柱的最大变形量不超过原立柱最大变形量的情况下，优化后的机床立柱的质量减轻了10.09%，前2阶频率分别提高了3.10%、2.42%，证明GA-GRNN优化机床立柱是可靠有效的，可以将其推广到更广泛的领域。

遗传算法；广义回归神经网络；均匀实验；灵敏度分析

0 引言

在现代航空航天产业高速发展的时代，越来越广泛的应用整体叶盘且呈现出多样化、复杂化的发展趋势[1]。在整体叶盘复合铣床机构中，立柱起着至关重要的支撑作用和基准作用，其强度、刚度及稳定性将直接影响到机床的加工精度、加工效率、抗振性及寿命。以往的经验法设计中，机床重量的80%用于保证机床的刚度，只有20%用于机床的运动[2]，因此，其进行轻量化设计十分必要。针对机床结构，国内外众多学者提出了许多优化和分析方法。CAO[3]等将全局灵敏度分析法运用于通用活塞式航空发动机的安全设计验证，他不仅将灵敏度分析应用到考虑不确定性因素和参数间交互作用的系统安全评估中，还展示了基于灵敏度分析的结果，如何提高安全设计水平；姚拴宝[4]等运用GRNN对高速列车头进行了优化设计，有效的减小了列车头部外形的气动阻力；Shahnewaz.M[5]等运用遗传算法和可靠性分析对带有FRP筋和箍筋加强筋的细长混凝土梁的剪切变形方程进行优化，使优化的方程具有更小的分散性。

由于仅仅使用灵敏度分析难以保证得到最优参数组合，所以首先采用灵敏度分析法找出对立柱的质量影响敏感的参数，再利用均匀试验表设计立柱需优化的尺寸参数的均匀试验，由文献[9]可知广义回归神经网络(GRNN)模型比其他任何神经网络模型精度都高，但很多仅仅用于预测模型，因此运用遗传算法(GA)对GRNN模型进行优化，得到最优尺寸参数组合，更进一步研究了GRNN模型。

1 基于灵敏度分析的立柱优化参数的选取

参数的灵敏度分析是通过一定的数学方法和手段，计算出参数对系统或模型的变化灵敏度，然后选择那些对系统或模型影响较大的设计参数，并根据灵敏度值的大小和正负，对设计参数进行优化[6]。

简化后的立柱独立变化的几何模型参数共15个，这15个参数又可以分为两类：一类参数基本不能更改，如螺纹孔直径、立柱外形尺寸等；另一类参数，在参数优化时可以更改。根据设计经验初步选定了6个参数作为设计变量，如图1、表1所示。参考原始设计尺寸，设置各设计变量的优化范围，然后进行尺寸的单参数敏感度分析，进一步减小设计变量的个数。选用应用最广泛的单参数敏感度分析方法——一次变化法[7]。

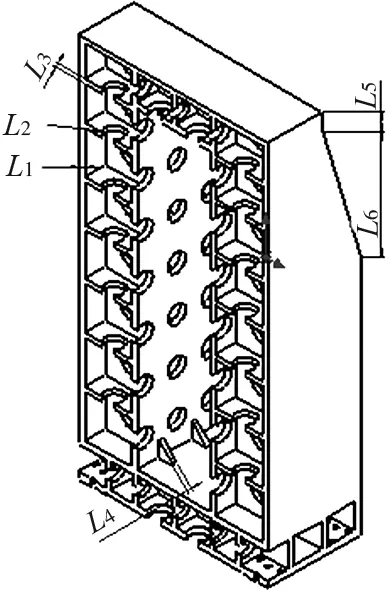
图1 立柱尺寸示意图

参数名称 尺寸数值/m立柱外壳厚度L10.04出砂孔直径L20.12内部筋板厚度L30.03外部筋板厚度L40.03立柱顶端台阶高度L50.12立柱背面斜坡高度L60.88

对于设计变量，其一阶频率敏感度定义为：

(1)

二阶频率敏感度为：

(2)

质量敏感度为：

(3)

为便于分析，这里引入敏感度评价指数βi，即将三类敏感度归一化后求和得到，值越大说明该尺寸相对于整体结构性能越敏感。

(4)

其中i=1，2,…，6。各尺寸敏感度分析结果如表2。

根据敏感度分析结果，最终确定设计变量个数为3个，设计变量为尺寸L1、L2、L3。为下文的GRNN建模做准备。

表2 立柱尺寸敏感度分析结果

2 基于GRNN的立柱优化模型建立

2.1 均匀实验及数据计算

表3 均匀试验设计的因素与水平

经过ANSYS Workbench分析计算后，得到的结果如表4。

表4 试验设计及计算结果

2.2 GRNN模型建立

广义回归神经网络 (Generalized Regression Neural Network, GRNN) 是美国学者 Donald F. Specht 提出的。它在逼近、预测、医药诊断、生物工程等方面有很强的预测能力，GRNN在实际应用中比其他任何神经网络都有较强的逼近功能[9]。

对于GRNN网络来说，确定了学习样本，则相应的网络结构和各神经元之间的连接权值也就确定了，网络的训练实际上只是确定光滑因子σ的过程。相对于传统的误差反向算法来说，GRNN在训练过程中无需调整神经元之间的连接权值，而是通过改变光滑因子σ来调整模式层中各单元的传递函数，以此获得最佳的回归估计的结果。

分别取机床立柱模型的尺寸变量L1、L2、L3为网络输入，取最大变形量δ、一阶频率f′、二阶频率f″、质量m为网络输出，构建GRNN模型，由于训练数据较少，采用交叉验证方法训练GRNN神经网络，并用循环找出最佳的SPREAD。各GRNN模型的最佳光滑因子如表5所示，网络训练后的误差如图2所示。

表5 GRNN模型的最佳光滑因子

图2 GRNN训练误差

由图2可知，各GRNN模型的训练误差最大值都在2.5%以下，均能满足精度要求。为说明本文所建立的GRNN神经网络模型的精确程度，故本文引入相关系数R的方法来验证[10]，

(5)

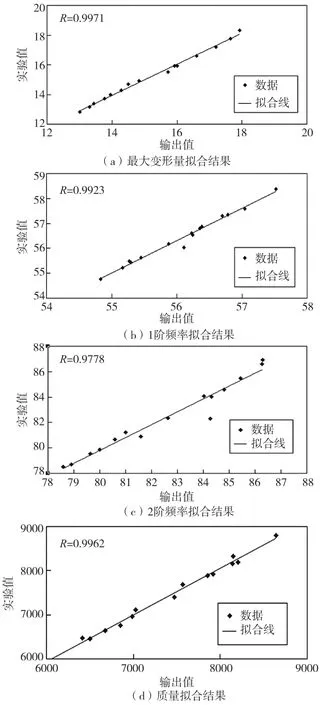
图3 神经网络响应面拟合

通过拟合结果可以看出，对于最大变形量的拟合度为99.71%，对于1阶固有频率的拟合度为99.23%，对于2阶固有频率的拟合度为97.78%。对于质量的拟合度为99.62%，拟合度均达到了97%以上，拟合效果良好。

3 基于遗传算法的模型优化

立柱优化的目标是在质量较轻的情况下提升其静态特性和动态特性，即质量和静变形量越小越好，低阶固有频率越大越好。静态特性直接关系到加工精度，为此至少要保证原结构静态特性，因此在优化模型中将其作为约束条件，将立柱质量作为目标函数，最终得到的优化设计的数学模型为:

min(m(X))

(6)

式中，δ0—原立柱最大变形量

δ(X)—立柱变形量

m(X)—立柱质量

神经网络训练拟合根据寻优函数的特点构建合适的GRNN,训练后的GRNN神经网络就可以预测函数输出。遗传算法极值寻优把训练后的GRNN预测结果作为个体适应度值，通过选择、交叉和变异操作，这3个算子在每一代进化中的历经性，使得遗传算法能够以概率方式进行全局搜索[11]，寻找函数的全局最优值及对应输入值。

GRNN训练结束后,可以用遗传算法寻找该非线性函数的最小值,遗传算法的迭代次数是100次,种群规模是15,交叉概率为0.4,变异概率为0.2，采用浮点数编码,个体长度为3，优化过程中最优个体适应度值变化曲线如图4所示。

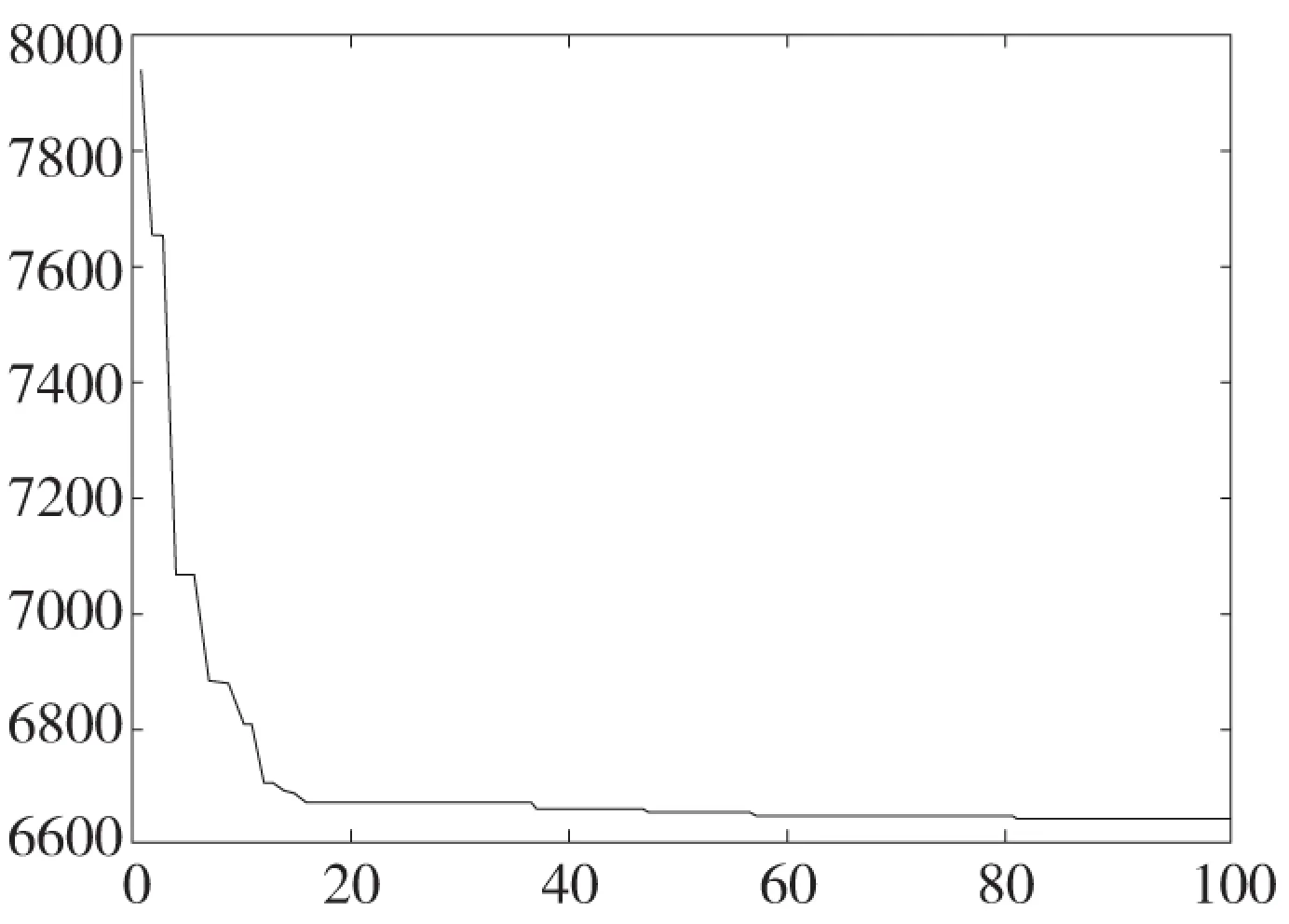
图4 适应度变化曲线

遗传算法得到的最优个体适应度值为6640.1，最优个体为[0.0451 0.1148 0.0100]，对尺寸进行取整，得到最终尺寸为：

L1=0.045m L2=0.115m L3=0.010m

对尺寸优化后的立柱进行有限元分析，得到优化前后的结果对比如图5、表6所示，优化后的立柱质量减轻了10.09%。

(a)优化前静力学分析结果 (b)优化后静力学分析结果

L1/mL2/mL3/m质量/kg1阶频率/Hz2阶频率/Hz最大变形量/μm优化前0.0400.1200.0307397.956.8882.3414.909优化后0.0450.1150.0106651.758.64386.33314.844

4 结论

对立柱的结构尺寸进行灵敏度分析，获得敏感尺寸参数，并通过GRNN建立优化数学模型，运用遗传算法对数学模型进行求解，获得尺寸最优解组合。在立柱的静动态性能基本不变的情况下，优化后的机床立柱质量减轻了10.09%，前2阶频率分别提高了3.10%、2.42%，实现了保证立柱刚性、减轻其重量、提高抗震性的目标。证明GA-GRNN算法优化机床立柱是可靠有效的，可以将其推广到更广泛的领域。

[1] 陈燕,周锟,牛凤丽,等.航空发动机整体叶盘磁力研磨光整实验[J].航空动力学报，2015,30(10):2323-2330.

[2] 胡亚辉，杨常青，许春雷，等.多目标优化在大型加工中心轻量化设计中的应用[J].机械科学与技术，2013,32(9):1342-1347.

[3] CAO Jiaokun, DING Shuiting. Sensitivity Analysis for Safety Design Verification of General Aviation Reciprocating Aircraft Engine[J].Chinese Journal of Aeronautics，2012(25): 675-680.

[4] 姚拴宝, 郭迪龙, 杨国伟.基于GA-GRNN 的高速列车头型三维优化设计[J].中国科学，2012,42(11):1283-1294.

[5] Shahnewaz. M, Machial. R, Alam. MS, et al. Optimized shear design equation for slender concrete beams reinforced with FRP bars and stirrups using Genetic Algorithm and reliability analysis [J].Engineering Structures,2016:151-165.

[6] 刘超峰,张功学,张淳,等.DVG850高速立式加工中心主轴箱灵敏度分析[J].组合机床与自动化加工技术,2010(10):88-90.

[7] 陆正争.软式飞艇参数敏感度分析与优化[D].哈尔滨：哈尔滨工业大学，2013.

[8] ZHOU Yongdao, FANG Kaitai, NING Jianhui. Constructing uniform designs: A heuristic integer programming method[J].Journal of Complexity，2012,28(2): 224-237.

[9] Fudi Chen, Hao Li, Zhihan Xu, et al. User-friendly optimization approach of fed-batch fermentation conditions for the production of iturin A using artificial neural networks and support vector machine[J].Electronic Journal of Biotechnology,2015(18):273-280.

[10] 谢水英, 黄芳.基于GRNN 神经网络的800H 合金热变形预测[J].热加工工艺，2014,43(12):45-50.

[11] 苗森春，杨军虎，王晓辉，等.基于神经网络-遗传算法的液力透平叶片型线优化[J].航空动力学报，2015,30(8):1918-1925.

(编辑 李秀敏)

Column Optimization of Compound Milling Machine Tool Based on GA-GRNN

GAO Ya-zhou, SHI Yao-yao

(The key Laboratory of Contemporary Design and integrated Manufacturing Technology Ministry of Education China, Northwestern Polytechnical University, Xi’an 710072, China)

The column is the main bearing components of compound milling machine tool, and the rigidity and dynamic performance of machine tool is affected by its' mass directly, and then so is the processing quality, so it is necessary to optimize and design the mass of compound milling machine tool. Firstly, the sensitivity analysis is used to obtain the sensitive dimension parameters that have influence on the column mass. Secondly, the approximate models of the mass of the column, the first two order frequency and the maximum deformation are established based on the uniform experiment and GRNN. And the approximate models are optimized by genetic algorithm to obtain the optimum combination of the dimension parameters. Finally, with the static and dynamic performance of the original column structure being almost the same, the mass of the optimized machine tool column is reduced by 10.1% and and the first two order frequency are increased by 26.84% and 0.91% respectively., which proves GA-GRNN is reliable and effective to optimize the machine tool column and it can be extended to more wide domain.

GA; GRNN; uniform experiment; sensitivity analysis

1001-2265(2016)10-0017-04

10.13462/j.cnki.mmtamt.2016.10.005

2016-06-07;

2016-06-22

国家科技重大专项资助项目(2013ZX04001-081)

高亚洲(1991—)，男，河南商丘人，西北工业大学硕士研究生， 研究方向为专用数控工艺装备，(E-mail) gaoyz226@163.com。

TH162;TG506

A