学会推理放飞思维

甘小生 李朝晖

推理是由一个或几个已知的判断（前提）推导出一个未知结论的思维过程，是数学的基本思维方式。教学中如何让学生通过观察、实验、归纳、类比等思维方法获得数学猜想，并进一步寻求证据、给出证明或举出反例？又如何让学生清晰、有条理地表达自己的思考过程并运用数学语言合乎逻辑地进行讨论和质疑呢？

人教版《数学》六年级上册《数学广角——数与形》一课旨在引导学生在数与形之间建立联系、发现规律，学会用数学语言清晰地表达思考过程。难点是让学生经历探索和验证规律的过程，掌握数形结合、归纳推理的数学思想，增强观察、归纳、类比、推理、探索规律的能力。笔者在教学中引导学生做了如下尝试。

一、仔细观察，发现异同，初见雏形

观察是小学数学常用的一种学习方法，是一切发现的基础。教学中教师要让学生明确观察的目的和方法，引导学生将观察与思考相结合，并在此基础上进行总结和归纳。

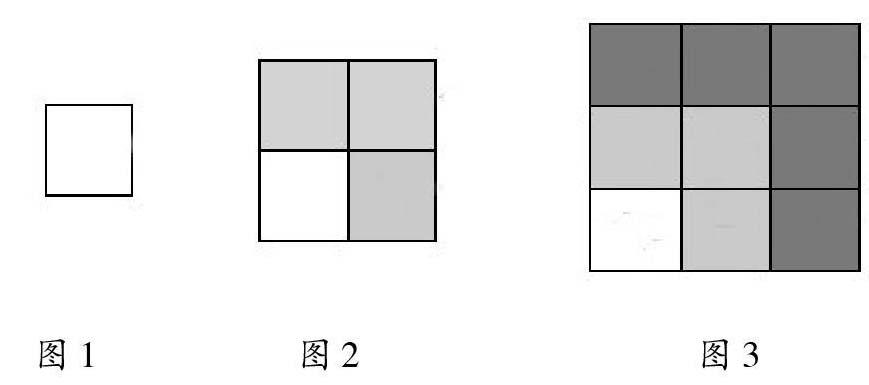
教学伊始，笔者出示图1、图2、图3，让学生仔细观察并思考：三个图形有什么相同或相似的地方？相邻两个图形之间有怎样的关联？学生思考后发现：每个大图形都是正方形；图2中有4个像图1那样的小正方形，图3中有9个；图2比图1增加了3个小正方形，图3比图2增加了5个小正方形……这样依次下去，各个图形中的小正方形个数分别是1，4，9……即1，1+3，1+3+5……；下一个图形与上一个图形相比，在外围增加一个“L”形图形。每个图形里每行与每列中小正方形个数相同。那么，又该如何用算式表示每个图形里小正方形的个数呢？学生的算法有两种：第一种—— 1×1=12=1（图1），2×2=22=4（图2），3×3=32=9（图3）；第二种—— 1=1=12（图1），1+3=4=22（图2），1+3+5=9=32（图3）。那么每个图形与相对应的算式又有什么关系？学生观察后发现：算式左边的加数是大正方形中右上角的小正方形和其它每一个“L”形图形所包含的小正方形个数之和，算式右边的数正好是每行或每列小正方形个数的平方。

以上教学中，笔者引导学生注意观察图形之间的相同或相似之处，观察并思考图形与数的对应关系。学生将严谨的数和直观的形有机结合起来，既发现了数的特征，又发现了和的规律。

二、合理猜想，有效验证，有序表述

建立在观察、思考之上的合理猜想是探索数学规律和寻求数学本质的一种有效策略。验证是为了证明猜想的合理性和正确性，常用方法有列举、归纳、动手操作等。提出猜想、验证猜想的过程中能充分发掘学生的探究意识和创新潜能。

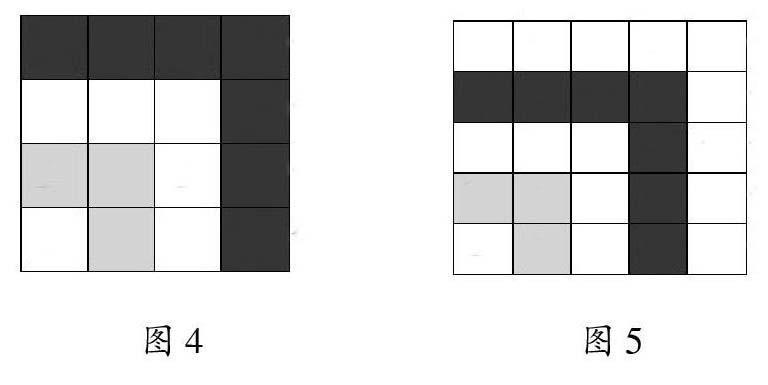
课中，笔者引导学生按照上面的发现提出自己的猜想，有学生提出：从1开始，几个连续的奇数相加的和就是几的平方。如何验证这一猜想呢？笔者引导学生继续思考“图4” 可能是什么样子？有几个这样的小正方形？怎么写算式？“图5”呢？学生思考后画出了图4、图5，发现图4中有16个小正方形，用算式表示是：1+3+5+7=42 ，图5中有25个小正方形，用算式表示是：1+3+5+7+9=52。接着，笔者让学生纵观五幅图及其对应的算式“1=12”“1+3=4=22 ”“1+3+5=9=32”“1+3+5+7=42”“1+3+5+7+9=52”并用简洁的数学语言表述一下其中的规律。学生指出：第几个图形，加数就有几个；加数个数是几，和就是几的平方；算式左边是从1开始连续的奇数的和，右边是一个数的平方。

以上教学中，笔者主要引导学生通过计算和动手画图两种方法验证猜想，并在验证过程中，鼓励学生有条理地表述，正确归纳出规律。

（作者单位：武汉市黄陂区长岭小学）