Nonlocal vibration analysis of circular double-layered graphene sheets resting on an elastic foundation subjected to thermal loading

Reza Ansari·Jalal Torabi



RESEARCH PAPER

Nonlocal vibration analysis of circular double-layered graphene sheets resting on an elastic foundation subjected to thermal loading

Reza Ansari1·Jalal Torabi1

Based on the nonlocal elasticity theory，the vibration behavior of circular double-layered graphene sheets（DLGSs）resting on the Winkler-and Pasternak-type elastic foundations in a thermal environment is investigated. The governing equation is derived on the basis of Eringen’s nonlocal elasticity and the classical plate theory（CLPT）. The initial thermal loading is assumed to be due to a uniform temperature rise throughout the thickness direction.Using the generalized differential quadrature（GDQ）method and periodic differential operators in radial and circumferentialdirections，respectively，the governing equation is discretized.DLGSs with clamped and simply-supported boundary conditions are studied and the influence of van der Waals（vdW）interaction forces is taken into account. In the numerical results，the effects of various parameters such aselastic mediumcoefficients，radius-to-thicknessratio，thermal loading and nonlocal parameter are examined on both in-phase and anti-phase naturalfrequencies.The results show that the thermal load and elastic foundation respectively decreases and increases the fundamental frequencies of DLGSs.

Circular DLGS·Vibration·Nonlocal theory· Thermal environment·Numerical solution

✉ Jalal Torabi jalal.torabii@gmail.com

1Department of Mechanical Engineering，University of Guilan，P.O.Box 3756，Rasht，Iran

1　Introduction

Nanostructures are widely used in various micro-and nano-scale devices such as gas detectors，biosensors，microelectro-mechanical systems（MEMS）and nano-electromechanical systems（NEMS）due to their superior mechanical，thermal，and electrical properties［1］.Among the nanostructures，carbon nanotubes（CNTs）and graphene sheets（GSs）have found a wide range ofapplications in engineering and medicine.

There exist three main categories for the theoretical modeling of nanomaterials.One category is atomistic modeling including some methods such as classical molecular dynamics（MD），tight-binding MDand the ab initio techniques.The other category is hybrid atomistic-continuum mechanics by which one can directly incorporate the continuum treatment into the interatomic potential［2］.The third approach is continuum modeling widely used in the analysis of materials at nano-scales.While conducting experiments at nanoscale is difficult，and the atomistic simulations are computationally expensive formodeling large scale nanostructures，the analysis ofnanomaterials based on the continuum mechanics is an interesting topic for researchers since the continuum models are computationally efficient and provide a reasonable accuracy.

Classic continuum models including the beam，plate，and shellmodelshave been used to simulate CNTsand GSs［3-5］. Atvery smallsizes，lattice spacing between individualatoms becomes significantly important，and the nanostructure cannot be considered as a continuous medium.In other words，the mechanicalbehaviorofnanostructures is size-dependent. Since the classic continuum models cannot capture the size effect，some higher-order continuum theories such as the modified couple stress theory［6，7］，the strain gradient the-ory［8，9］，the surface stress theory［10-13］，and the nonlocal elasticity theory［14-17］can be employed for the analysis of small-scale systems.In addition，Peddieson et al.［18］indicated that the nonlocal elasticity theory can be appropriately applied to nanotechnology applications.An important issue related to nonlocal models is the appropriate value of nonlocal parameters.The suitable value of the nonlocal parameter can be determined by matching the results obtained from experiments or atomistic methods such as MD simulations to those of nonlocal models.In this regard，some attempts have been made for calibrating the nonlocal parameter in some nonlocal models［19-22］.

In addition to the direct applications of GSs in different fields，they are the basic structural elements for carbon nanotubes，fullerenes，and nanorings Thus，understanding the mechanicalbehaviorof GSs is ofgreatimportance in designing MEMS and NEMS.Application of nonlocal elasticity theory has been reported by many researchers in the static and dynamic analyses of GSs.

To be noted is that Gibson et al.［23］indicated employing the nonlocal elasticity theory results in accurate prediction of vibration behavior of nanostructures.Bending，vibration，and buckling ofrectangularand circular GSs have been studied by differentresearchers［24-34］.Forexample，Arash and Wang［35］investigated the vibration of single-and doublelayered graphene sheets（SLGSs and DLGSs）using the nonlocal elasticity theory and molecular dynamics simulations.The nonlocal parameter was calibrated through the verification of natural frequency obtained by the nonlocal elasticity theory and molecular dynamics simulations. Employing the differential quadrature method and the nonlocal elasticity theory，Pradhan and Kumar［36］studied the vibration of orthotropic rectangular graphene sheets. The effects of nonlocal parameters，material properties，and boundary conditions on the non-dimensional frequency of GSs were presented.In addition，Jomehzadeh and his coworkers［37，38］investigated the large amplitude vibration of DLGSs resting on a nonlinear polymer matrix.Using Hamilton’s principle and von-Karman’s nonlinear geometricalmodel，the governing equations of DLGSs were obtained. The influences of nonlocal parameters and nonlinear behavior of a polymer matrix on the nonlinear vibration analysis of DLGSs were considered.

Using the nonlocal continuum model，the effects of small scale on the vibration of quadrilateral nanoplates were studied by Babaei and Shahidi［39］.The Galerkin method is employed to obtain the non-dimensional natural frequencies of skew，rhombic，trapezoidal，and rectangular nanoplates. Moreover，considering the nonlocalelasticity theory，Murmu et al.［40］studied the effects of a magnetic field on the vibration of rectangular SLGSs resting on elastic foundations. The results reveal that the in-plane magnetic field increases the natural frequencies of the SLGSs.Also，Mohammadi et al.［41］examined the free vibration of embedded circular and annular SLGSs employing the nonlocal continuum model.Furthermore，Mohammadi and his co-workers investigated the influence of thermo-mechanical pre-load on the vibration behavior of embedded SLGSs［42］.

The free vibration behaviorofrectangularGSs undershear in-plane loads was studied by Mohammadi et al.［43］based on the nonlocalelasticity theory.They employed the differentialquadrature method to solve the problem.In thatwork，the influences ofsurrounding elastic medium and boundary conditions were studied on the vibrations of orthotropic SLGSs. Asemi et al.［44］investigated the axisymmetric buckling of circular SLGS by decoupling the nonlocal equations of Eringen theory.The governing equations were derived using equilibrium equations of the circular plate in polar coordinates，and the Galerkin method wasimplemented to compute the buckling loads.

Then Shen et al.［45］presented the nonlinear vibration analysis of rectangular DLGSs in thermal environments using MDsimulationsand the nonlocalelasticity.The nonlinear von-Karman relations were considered and the nonlocal parameterwas calibrated by equating the naturalfrequencies of GSs obtained from the MD simulations and those from the nonlocal plate model.In addition，the nonlocal vibration of DLGSs-based resonators was studied by Shi et al.［46］. By utilizing the nonlocal thin plate theory，both the in-phase mode（IPM）and the anti-phase mode（APM）of vibrational behavior of DLGSs with simply-supported boundary conditions were investigated.Employing the finite strip method and considering the van der Waals（vdW）effect，Sarrami-Foroushani and Azhari［47］analyzed the nonlocal vibration and stability behaviors of single-and multi-layered rectangular GSs.

In the present study，the nonlocal vibration behavior of embedded circular DLGSs subjected to thermal load is studied.Based on the nonlocalelasticity theory，the classicalplate theory（CLPT），and the governing equation is derived.Both Winkler-and Pasternak-type elastic foundations are taken into account.A uniform temperature rise throughout the thickness direction is considered as a thermal loading.An efficient numerical method is employed to solve the governing equation and obtain the naturalfrequencies ofthe DLGSs. Using the generalized differential quadrature method and periodic differential operators in radial and circumferential directions，respectively，the governing equation is discretized in two directions.Employing the generalized differential quadrature（GDQ）method in the circumferential direction one should satisfy the periodicity condition on the boundary. While applying the periodic differential operators in the circumferentialdirection，the periodicity condition willbe satisfied by itself.DLGSswith clamped（C）and simply-supported（S）boundary conditions are studied.Furthermore，considering the vdW interaction forces between layers of DLGSs，the effects of elastic medium and thermal loadings on both in-phase and anti-phase natural frequencies were examined.

2　Governing equations

Unlike the classical continuum mechanics，which states that the stress tensor at a reference point x can be defined by the strain tensor at that point，based on the nonlocal elasticity theory proposed by Eringen［14］，the stress at a reference point x of a body is a function of the strain field at every point in the medium.According to the nonlocal elasticity theory，the nonlocal stress tensor can be defined as

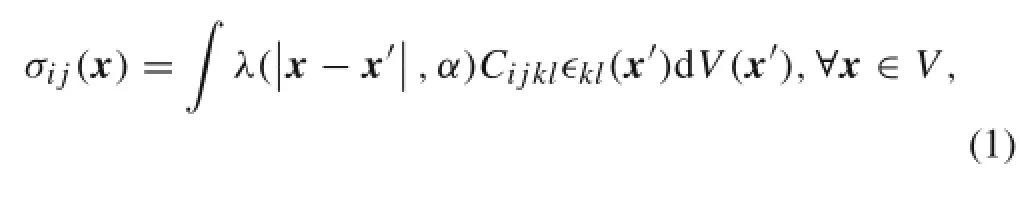
where σij，ϵij，and Cijklare elements of the stress，strain，and fourth-order elasticity tensor，respectively.Kernel functionis the nonlocal modulus which depends on the Euclidean distance，and a material constant α=e0a/l，where e0，a，and l are the material constant，internal characteristic lengths，and external characteristic lengths，respectively.The parameter e0a is the nonlocalparameter which captures the size effect in the behavior of the nanoscale structures.Eringen defined the kernel functionas

where K0is the modified Bessel function and x·x presents the neighborhood distance［14］.Considering Eqs.（1）and（2），the differential form of the constitutive relation could be obtained as

where is the Laplacian operator.On the basis of Eq.（3）and considering the CLPT，the plane stress condition and thermal effects，the stress-strain relations are written as

Fig.1 A continuum plate model of the circular graphene sheet

where E，G，ν，and α are Young’s modulus，shear modulus，Poisson’s ratio，and the coefficient of thermal expansion，respectively.A continuum plate model of the circular graphene sheet and associated coordinates are shown in Fig.1.Based on the classical plate theory，the threedimensional displacement components U，V，and W are assumed as

where u，v，and w are the displacement components of the middle surface of the graphene sheet，and t denotes time. Since neglecting the displacements of the middle surface along the radial and circumferential directions，i.e.，u=0，v=0，does not affect the transverse vibration behavior of GSs，the strain fields can be expressed as

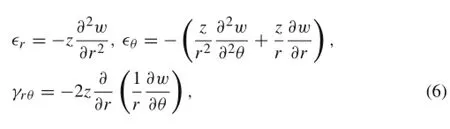
where z denotes the distance from the middle surface.The stress resultants can be given as

Substituting Eqs.（4）-（6）into Eq.（7）gives

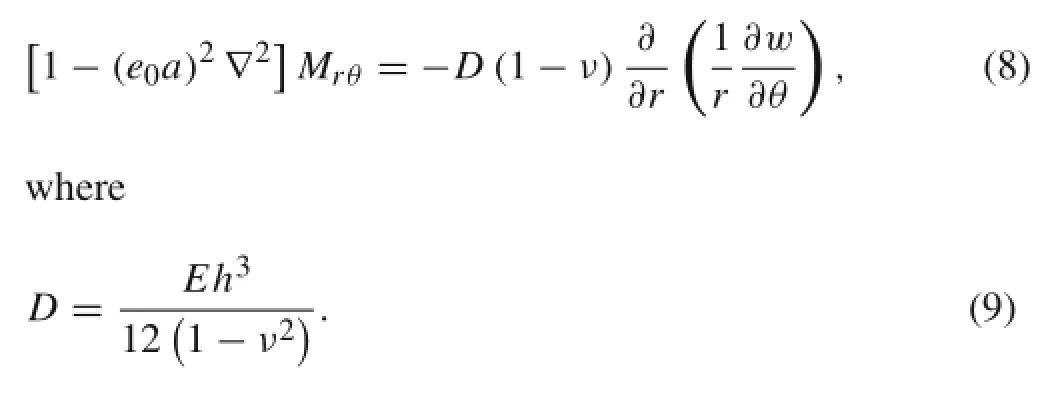
From Eqs.（3）-（7），the governing equation of vibration of a pre-loaded circular plate resting on a Pasternak-type elastic foundation can be derived as

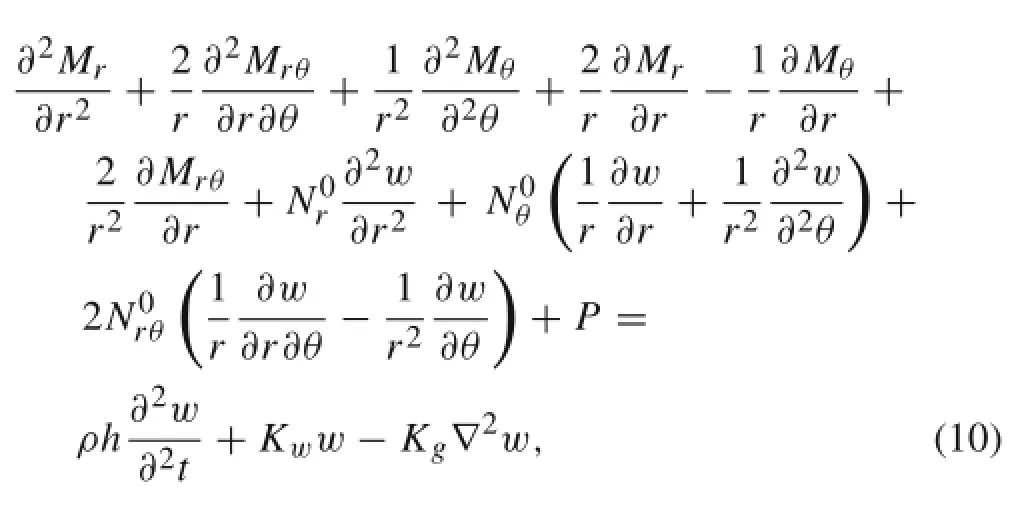
where h，P，ρ，Kw，and Kgare thickness，distributed transverse pressure，density，Winklermodulus，and shearmodulus of the surrounding elastic medium，respectively.In addition，are stress resultants due to initial thermal loading.Assuming uniform temperature rise throughout the thickness direction and considering the linear equilibrium equation of the plate，the thermal stress resultants on the basis of the theory of thermal elasticity，can be written as

Using Eqs.（8），（10），and（11），the equation ofmotion in terms of lateral deflection can be obtained as

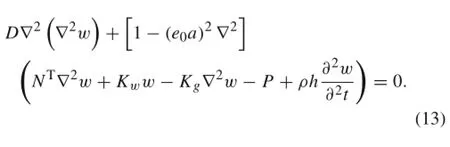
Since a DLGS is composed of two layers of GS，Eq.（13）can be extended into two equations for the upper and lower layers as

where the superscripts 1 and 2 indicate the upper and lower layers of the circular DLGSs，respectively.In addition，P1and P2are the applied pressure on the GSs through the vdW interaction forces，which can be given as

where c is the vdW interaction coefficient between two layers，which can be obtained from the Lennard-Jones pair potential as［46］

where a is the characteristic internal length of the C-C bond. ζ=2.968 MeV and δ=0.3407 nm are parameters chosen to fit the physical properties of GSs and（j= 1，2）.

3　Solution procedure

The equationsofmotion ofDLGSs resting on an elastic foundation and subjected to initial thermal loading are obtained based on the nonlocal CLPT.Using the GDQ method in radial direction and periodic differential matrix operators in the circumferential direction，the governing equation（14）will be discretized in two dimensions to find the natural frequency of DLGSs.In this regard，the GDQ method and periodic differential operators will be presented in the next section.

3.1GDQ method

On the basis of the GDQ method［48］，the n-th derivative of f（r）can be obtained as a linear sum of the function，i.e.，

in which Nris the numberoftotaldiscrete grid pointsused in the process of approximation in the r direction andthe weighting coefficients. A column vector F can be defined as shows

where frjdenotes the nodal value of f（r）at r=rj.A differential matrix operator based on Eq.（17）can be written in the form

In Eq.（20），n is the orderofdifferentiation andis obtained by［49］

in which Iris an Nr×Nridentity matrix and

Previous studies revealed thatthe Chebyshev-Gauss-Lobatto grid point distribution has the most convergence and stability among the other grid distributions.Thus，using this grid distribution，the mesh in the radialdirection can be generated as

where R is the radius of the circular GSs.

3.2Periodic differential operators

To find out the periodic response of circular GSs in the circumferential direction，the general governing equation is discretized overthe circumferentialdirection via periodic differentialmatrix operators.Using this method，the periodicity condition will be naturally satisfied，and one does not need to impose the periodicity condition on differential operators. Considering an unbounded grid with periodic grid points between 0 and 2π and employing the derivatives of periodic sinc function，as a base function in a collocation method，the spectral differentiation matrix operators are obtained.The periodic differential matrix operators are defined as［49］

where the coefficients ai，jand bi，jare given as

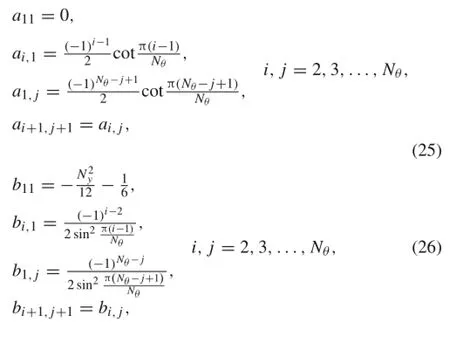
where Nθis the number of grid points in the circumferential direction.

3.3Discretization of governing equation

The equation of motion of DLGSs will be discretized using the GDQ method and periodic differential matrix operator. The nodal values of lateral deflection of each GS layers are given as

where Iθis an Nθ×Nθidentity matrix and⊗denotes the Kronecker product.Using Eqs.（27）and（28）and assuming

harmonic solution in time domain，i.e.and，the governing equation（14）can be written as

in which∇0=Iθ⊗Irand

Substituting the boundary conditions into the stiffness and inertia matrices and solving the set of linear Eq.（29），the two kinds of natural frequencies of DLGSs ωIPMand ωAPMare obtained.The subscripts IPM and APM denote the inphase mode and anti-phase mode，respectively.Considering Eq.（29），two sets of linear algebraic equations for IPM and APM natural frequencies can be written as

4　Results and discussion

On the basis of Eringen’s nonlocal elasticity and the classical plate theory，the vibration analysis of embedded circular DLGSs was carried out in a thermal environment. The mechanical properties of GSs are assumed as follows: Young’s modulus E=1 TPa，the mass density ρ= 2300 kg/m3，Poisson’s ratio ν=0.3，the thermal expansion coefficient for high temperature case α=1.1×10-6◦C-1，and the thickness of GSs h=0.34 nm［42］.The effects of Winkler and Pasternak coefficients of elastic foundation are taken into account.In this regard，non-dimensional coefficients of elastic medium are defined as

Since the vibrational behavior of GSs is studied under initial thermal loading，the natural frequency of the structure becomes zero when the thermal loading meets its critical value.Both the IPM and the APM of natural frequency are assessed according to Eq.（33）.

The accuracy of the present work is verified by the given results for the non-dimensional natural frequency of SLGSs by Mohammadi et al.［41］.Comparison of dimensionlessfrequencies for various nonlocal parameters is presented in Table 1.Moreover，the influences of various elastic foundation coefficients on the dimensionless frequency of SLGS are compared in Table 2.The results of both tables are in good agreement.

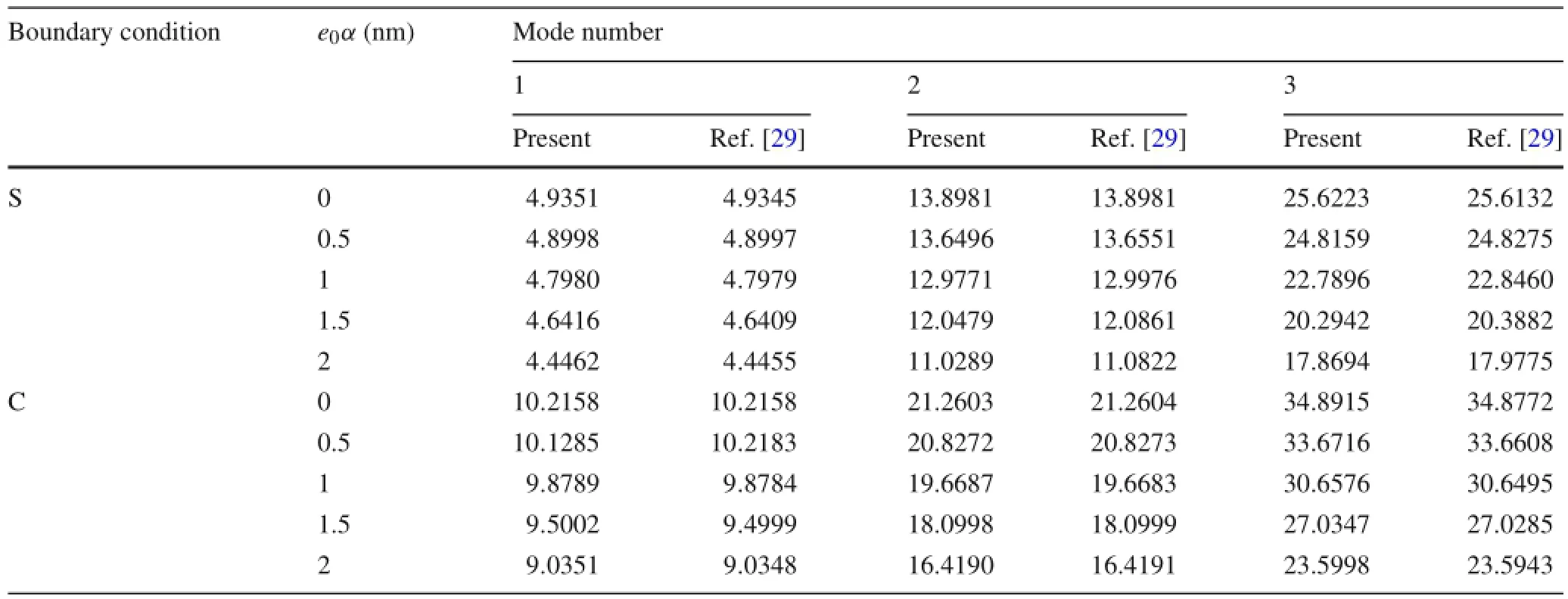
Table 1 Comparison of dimensionless frequency parameters for two different boundary conditions and nonlocal parameters（R=10 nm）

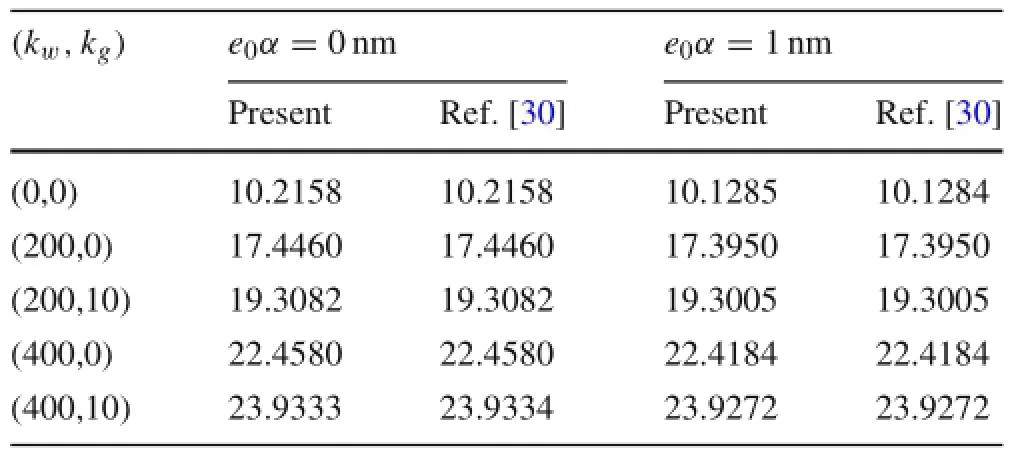
Table 2 Comparison of dimensionless frequency parameters for variouselastic foundation coefficientsand nonlocalparametersforclamped boundary condition（R=20 nm）

Table 4 Changes of IPM natural frequencies（THz）of clamped DLGS forvariousthermalloadingsand nonlocalparameters（R/h=50，kw= 0，kg=0）

The effects of elastic foundation coefficients and nonlocal parameter on IPM and APM natural frequencies of simply-supported DLGSs for different mode numbers are presented in Table 3.The values of nonlocal parameter are assumed to be 0（corresponding to the classical/local continuum model）and 2nm.The results show that the increase of the nonlocalparameterconsiderably reduces the IPMnatural frequencies.For APM，however，the effect of nonlocal parameter on the fundamental frequency is almost negligible due to the influential effect of the vdW interaction forces.The nonlocality continues to affect APM frequencies at higher mode numbers.In addition，itcan be seen thatthe increase of the elastic foundation coefficients increases the natural fre-quencies，whereas，these changes decrease at higher mode numbers.

Table 3 Changes of IPM and APM natural frequencies（THz）of simply-supported DLGS for various elastic foundation coefficients and nonlocal parameters（R/h=10）

Table 5 Changes of IPM natural frequencies（THz）of DLGS for different thermal loadings and boundary conditions（R/h=10）

Fig.2 IPM natural frequencies versus mode numbers（R/h=10，kw=0，kg=0）

Variations ofIPMnaturalfrequency ofclamped DLGSsin respect to increase of the temperature differences and nonlocal parameters are given in Table 4.The results indicate that the natural frequencies decrease by increasing the temperature difference.At higher mode numbers，the influences of thermal loading are weakened.

IPM natural frequencies of DLGSs for different nonlocal parameters，boundary conditions，elastic foundation coefficients and thermal loadings are presented in Table 5.In addition to whatwas mentioned above，itisseen thatthe presence of elastic foundation decreases the effects of thermal loading on the fundamental frequency of the simply supported GSs.

The variations of IPM and APM natural frequencies of clamped and simply-supported GSs versus mode numbers for various nonlocal parameters are shown in Figs. 2 and 3，respectively.It is observed that the natural frequencies of the DLGSs are more sensitive to nonlocal parameter at higher mode numbers.Furthermore，considering the clamped boundary condition makes the GSs stiffer and results in higher natural frequency in comparison with simply-supported one.

Fig.3 APM natural frequencies versus mode numbers（R/h=10，kw=0，kg=0）

Fig.4 IPM fundamental frequencies versus radius-to-thickness ratio（kw=0，kg=0）

The changes of IPM and APM natural frequencies of clamped and simply-supported GSs versus the radius-tothickness ratios for various nonlocal parameters are demonstrated in Figs.4 and 5.The results reveal that the effects of nonlocal parameter at higher R/h ratios can be neglected，which is in agreement with nonlocal elasticity theory.Moreover，the vdW interaction forces play an important role on size dependency of APM natural frequencies and decrease the effects of nonlocal parameter.

Figure 6 depicts the variations of IPM fundamental frequencies of GSs versus the radius-to-thickness ratios forvarious elastic foundation coefficients.It is found that at higher R/h ratios，the influences of elastic medium coefficients diminish.

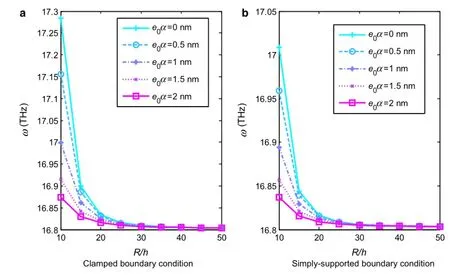
Fig.5 APM third natural frequency versus radius-to-thickness ratio（kw=0，kg=0）

Fig.6 IPM natural frequencies versus radius-to-thickness ratio（e0α=1 nm）

The variations of APM fundamental frequencies versus vdW interaction coefficients for various nonlocal parameters are plotted in Fig.7.It is observed that the quantities of vdW interaction coefficients play an important role on the size-dependency of the APM natural frequency.In addition，the higher vdW interaction coefficients lead to the higher values of natural frequency of DLGSs，as it is expected.

Figure 8 presents the variations of IPM natural frequencies of clamped and simply-supported GSs versus the temperature differences through the thickness direction for various nonlocal parameters.The results obviously indicate that the fundamental natural frequencies of GS are size-dependent.Additionally，the fundamental frequencies decrease with the increase of thermal loading and tend to zero when the thermal loadings meet their critical values.

Fig.7 APM natural frequencies versus vdW interaction coefficients（R/h=10，kw=0，kg=0）

Fig.8 IPM natural frequencies versus Temperature rise（R/h=50，kw=0，kg=0）

5　Conclusion

The size-dependent vibration of circular DLGSs resting on an elastic foundation and subjected to thermal loading was investigated.Employing the nonlocal elasticity theory，the governing equations of DLGSs were derived.The Pasternaktype elastic foundation was considered.In addition，the thermal loading was considered to be due to a uniform temperature rise throughout the thickness direction.

Using the generalized differential quadrature method in the radial direction and periodic differential operators in the circumferential direction，the governing equations were discretized.Considering the vdW interaction forces，both inphase and anti-phase natural frequencies were examined.

Itwas observed thatthe nonlocalparameterhas significant effects on the natural frequencies of circular DLGSs.The higher mode numbers of IPM and APM natural frequencies are more sensitive to size-dependency.The results showed that the increase of elastic foundation coefficients increases the natural frequencies of DLGSs.Also，increase in R/h ratiosmakesthe naturalfrequency lesssensitive to increase of the elastic medium coefficients.In addition，itwas figured out that thermal loadings play an important role on the vibration analysis of DLGSs，as increase of the temperature difference yieldsto reduction offundamentalfrequency.Moreover，in the presence of an elastic foundation，considering the simply-supported boundary conditions decreases the effects of thermal loading on the fundamental frequency of the GSs.

1.Li，X.，Bhushan，B.，Takashima，K.，etal.:Mechanicalcharacterization of micro/nanoscale structures for MEMS/NEMS applications using nanoindentation techniques.Ultramicroscopy 97，481-494（2003）

2.Belytschko，T.，Xiao，S.P.，Schatz，G.C.，et al.:Atomistic simulations of nanotube fracture.Phys.Rev.B 65，235430（2002）

3.Natsuki，T.，Matsuyama，N.，Shi，J.X.，et al.:Vibration analysis of nanomechanical mass sensor using carbon nanotubes under axial tensile loads.Appl.Phys.A 116，1001-1007（2014）

4.Natsuki，T.，Shi，J.X.，Ni，Q.Q.:Vibration analysis of circular double-layered graphene sheets.J.Appl.Phys.111，044310（2012）

5.Wang，J.，He，X.，Kitipornchai，S.，et al.:Geometrical nonlinear free vibration of multi-layered graphene sheets.J.Phys.D Appl. Phys.44，135401（2011）

6.Yang，F.A.C.M.，Chong，A.C.M.，Lam，D.C.C.，etal.:Couple stress based strain gradient theory for elasticity.Int.J.Solids Struct.39，2731-2743（2002）

7.Park，S.K.，Gao，X.L.:Bernoulli-Euler beam model based on a modified couple stress theory.J.Micromech.Microeng.16，2355（2006）

8.Mindlin，R.D.，Eshel，N.N.:On first strain-gradient theories in linear elasticity.Int.J.Solids Struct.4，109-124（1968）

9.Ansari，R.，Gholami，R.，Shojaei，M.F.，etal.:Size-dependentbending，buckling and free vibration offunctionally graded Timoshenko microbeamsbased on the mostgeneralstrain gradienttheory.Compos.Struct.100，385-397（2013）

10.Gurtin，M.E.，Weissmüller，J.，Larche，F.:A general theory of curved deformable interfacesin solidsatequilibrium.Philos.Mag. A 78，1093-1109（1998）

11.Dingreville，R.，Qu，J.，Cherkaoui，M.:Surface free energy and its effect on the elastic behavior of nano-sized particles，wires and films.J.Mech.Phys.Solids 53，1827-1854（2005）

12.Farajpour，A.，Rastgoo，A.，Mohammadi，M.:Surface effects on the mechanical characteristics of microtubule networks in living cells.Mech.Res.Commun.57，18-26（2014）

13.Asemi，S.R.，Farajpour，A.:Decoupling the nonlocal elasticity equations for thermo-mechanical vibration of circular graphene sheetsincluding surface effects.Phys.ELow Dimens.Syst.Nanostruct.60，80-90（2014）

14.Eringen，A.C.:On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves.J.Appl.Phys. 54，4703-4710（1983）

15.Rahmani，O.，Jandaghian，A.A.:Buckling analysis of functionally graded nanobeams based on a nonlocal third-order shear deformation theory.Appl.Phys.A 119，1019-1032（2015）

16.Moosavi，H.，Mohammadi，M.，Farajpour，A.，et al.:Vibration analysis of nanorings using nonlocal continuum mechanics and shear deformable ring theory.Phys.E Low Dimens.Syst.Nanostruct.44，135-140（2011）

17.Mohammadi，M.，Farajpour，A.，Moradi，A.，et al.:Shear buckling of orthotropic rectangular graphene sheet embedded in an elastic medium in thermalenvironment.Compos.PartBEng.56，629-637（2014）

18.Peddieson，J.，Buchanan，G.R.，McNitt，R.P.:Application of nonlocal continuum models to nanotechnology.Int.J.Eng.Sci.41，305-312（2003）

19.Duan，W.H.，Wang，C.M.，Zhang，Y.Y.:Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics.J.Appl.Phys.101，24305-24305（2007）

20.Ansari，R.，Rouhi，H.:Analytical treatment of the free vibration of single-walled carbon nanotubes based on the nonlocalFlugge shell theory.J.Eng.Mater.Technol.134，011008（2012）

21.Ansari，R.，Rouhi，H.，Sahmani，S.:Calibration of the analytical nonlocal shell model for vibrations of double-walled carbon nanotubes with arbitrary boundary conditions using molecular dynamics.Int.J.Mech.Sci.53，786-792（2011）

22.Aydogdu，M.:Longitudinal wave propagation in nanorods using a general nonlocal unimodal rod theory and calibration of nonlocal parameter with lattice dynamics.Int.J.Eng.Sci.56，17-28（2012）

23.Gibson，R.F.，Ayorinde，E.O.，Wen，Y.F.:Vibrations of carbon nanotubes and their composites:a review.Compos.Sci.Technol.67，1-28（2007）

24.Pradhan，S.C.，Phadikar，J.K.:Small scale effect on vibration of embedded multilayered graphene sheets based on nonlocal continuum models.Phys.Lett.A 373，1062-1069（2009）

25.Mohammadi，M.，Moradi，A.，Ghayour，M.，et al.:Exact solution for thermo-mechanical vibration of orthotropic mono-layer graphene sheet embedded in an elastic medium.Lat.Am.J.Solids Struct.11，437-458（2014）

26.Shen，L.E.，Shen，H.S.，Zhang，C.L.:Nonlocal plate model for nonlinearvibration ofsingle layergraphene sheetsin thermalenvironments.Comput.Mater.Sci.48，680-685（2010）

27.Ansari，R.，Rajabiehfard，R.，Arash，B.:Nonlocal finite element model for vibrations of embedded multi-layered graphene sheets. Comput.Mater.Sci.49，831-838（2010）

28.Ansari，R.，Sahmani，S.，Arash，B.:Nonlocal plate model for free vibrations of single-layered graphene sheets.Phys.Lett.A 375，53-62（2010）

29.Shen，H.S.，Shen，L.，Zhang，C.L.:Nonlocalplatemodelfornonlinearbending ofsingle-layergraphene sheetssubjected to transverse loads in thermalenvironments.Appl.Phys.A 103，103-112（2011）

30.Pradhan，S.C.，Murmu，T.:Small scale effect on the buckling of single-layered graphene sheets under biaxial compression via nonlocal continuum mechanics.Comput.Mater.Sci.47，268-274（2009）

31.Pradhan，S.C.，Phadikar，J.K.:Scale effect and buckling analysis of multilayered graphene sheets based on nonlocal continuum mechanics.J.Comput.Theor.Nanosci.7，1948-1954（2010）

32.Farajpour，A.，Mohammadi，M.，Shahidi，A.R.，et al.:Axisymmetric buckling of the circular graphene sheets with the nonlocal continuum plate model.Phys.E Low Dimens.Syst.Nanostruct. 43，1820-1825（2011）

33.Mohammadi，M.，Goodarzi，M.，Ghayour，M.，et al.:Influence of in-plane pre-load on the vibration frequency of circular graphene sheet via nonlocal continuum theory.Compos.Part B Eng.51，121-129（2013）

34.Mohammadi，M.，Farajpour，A.，Goodarzi，M.，et al.:Temperature effect on vibration analysis of annular graphene sheet embedded on visco-pasternak foundation.J.Solid Mech.5，305-323（2013）

35.Arash，B.，Wang，Q.:Vibration of single-and double-layered graphene sheets.J.Nanotechnol.Eng.Med.2，011012（2011）

36.Pradhan，S.C.，Kumar，A.:Vibration analysis of orthotropic graphene sheets using nonlocal elasticity theory and differential quadrature method.Compos.Struct.93，774-779（2011）

37.Jomehzadeh，E.，Saidi，A.R.:A study on large amplitude vibration of multilayered graphene sheets.Comput.Mater.Sci.50，1043-1051（2011）

38.Jomehzadeh，E.，Saidi，A.R.，Pugno，N.M.:Large amplitude vibration ofa bilayergraphene embedded in anonlinearpolymermatrix. Phys.E Low Dimens.Syst.Nanostruct.44，1973-1982（2012）

39.Babaei，H.，Shahidi，A.R.:Vibration of quadrilateral embedded multilayered graphene sheets based on nonlocalcontinuum models using the Galerkin method.Acta Mech.Sin.27，967-976（2011）

40.Murmu，T.，McCarthy，M.A.，Adhikari，S.:In-plane magnetic field affected transverse vibration of embedded single-layer graphene sheets using equivalent nonlocal elasticity approach.Compos. Struct.96，57-63（2013）

41.Mohammadi，M.，Ghayour，M.，Farajpour，A.:Free transverse vibration analysis of circular and annular graphene sheets with various boundary conditions using the nonlocal continuum plate model.Compos.Part B Eng.45，32-42（2013）

42.Mohammadi，M.，Farajpour，A.，Goodarzi，M.，et al.:Thermomechanical vibration analysis of annular and circular graphene sheet embedded in an elastic medium.Lat.Am.J.Solids Struct. 11，659-682（2014）

43.Mohammadi，M.，Farajpour，A.，Goodarzi，M.:Numerical study of the effect of shear in-plane load on the vibration analysis of graphene sheet embedded in an elastic medium.Comput.Mater. Sci.82，510-520（2014）

44.Asemi，S.R.，Farajpour，A.，Borghei，M.，et al.:Thermal effects on the stability of circular graphene sheets via nonlocal continuum mechanics.Lat.Am.J.Solids Struct.11，704-724（2014）

45.Shen，H.S.，Xu，Y.M.，Zhang，C.L.:Prediction of nonlinear vibration of bilayer graphene sheets in thermal environments via molecular dynamics simulations and nonlocal elasticity.Comput. Methods Appl.Mech.Eng.267，458-470（2013）

46.Shi，J.X.，Ni，Q.Q.，Lei，X.W.，et al.:Nonlocal vibration analysis of nanomechanical systems resonators using circular double-layer graphene sheets.Appl.Phys.A 115，213-219（2014）

47.Sarrami-Foroushani，S.，Azhari，M.:Nonlocal vibration and buckling analysis of single and multi-layered graphene sheets using finite strip method including van der Waals effects.Phys.E Low Dimens.Syst.Nanostruct.57，83-95（2014）

48.Shu，C.:DifferentialQuadratureand itsApplication in Engineering. Springer，London（2000）

49.Ansari，R.，Mohammadi，V.，Shojaei，M.F.，et al.:Nonlinear vibration analysis of Timoshenko nanobeams based on surface stress elasticity theory.Eur.J.Mech.A Solids 45，143-152（2014）

2 December 2015/Revised:9 February 2016/Accepted:12 April 2016/Published online:20 June 2016

©The Chinese Society of Theoretical and Applied Mechanics；Institute of Mechanics，Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016