Stress analysis of thermally affected rotating nanoshafts with varying material properties

Keivan Kiani



RESEARCH PAPER

Stress analysis of thermally affected rotating nanoshafts with varying material properties

Keivan Kiani1

Based on the surface elasticity theory of Gurtin-Murdoch，thermo-elastic fields within rotating nanoshafts with varying material properties subjected to a thermal field are explicitly examined.Accounting for the surface energy effect，the nonclassical boundary conditions are enforced in the cases of fixed-free and free-free conditions.The effects of variation of material properties，temperature of the environment，angular velocity，and radius of the outer radius on the radial displacement，hoop and radial stresses are investigated.In all performed studies，the role of the surface effect on the thermo-elastic field of the nanostructure is methodically discussed.

Rotating nanoshaft·Thermo-elastic field· Surface energy effect·Non-classical boundary conditions· Analytical modeling

1　Introduction

The advancement of noncontact methods to rotate nanorods，nanowires and nanotubes is ofgreatsignificance forexploitation of them as main members of the upcoming nanomotors. There is much evidence regarding rotation of microneedles［1］，asymmetric nanorods［2］，octapolar metal nanoparticles［3］，nanowires［4］，and nanotube bundles［5］by application of light or focused laser beams.In fact，these achievements of scientists have opened new horizons forfabrication of nanomachines that operate with continuous rotational motion.Since these nanometer-sized rotary motors do not required mechanical contact and electrical wires，a wide range of applications can be imagined for them from medicine to manufacturing.For example，these nanomachines can be used as fluid pumpers in microfluidic chips［6，7］and nanotweezers［8，9］.However，many experiments have been reported for such nanorotors，but their mechanical analyses have not yet been performed.To bridge this scientific gap，herein，we focus on elastic deformation and stresses resulting from rotational motion of a nanoshaft in a thermal environment.

✉ Keivan Kiani k_kiani@kntu.ac.ir；keivankiani@yahoo.com

1Department of Civil Engineering，K.N.Toosi University of Technology，P.O.Box 15875-4416，Tehran，Iran

For structures with dimensions at the nanoscale，the ratio of the surface area to the bulk volume is much greater than the macrostructures.It indicates that if the nanostructure is acted upon by external loads，the ratio of the elastic strain energy of the surface layer to that of the bulk would be noticeable and such a fact should be appropriately considered in modeling of the nanostructure.One of the most famous surface elasticity models is that developed by Gurtin and Murdoch［10-12］.In the context of such a theory，the surface layer is one of two major constituents of the nanostructure whose thickness is negligible. This layer is tightly attached to the underlying bulk zone. Since no slippage is allowed at the interface of the surface layer and the bulk zone，the displacements of the surface layer are exactly the same as those of the bulk at the vicinity of the surface.The mechanical behavior of the surface layer is completely different from that of the bulk.This leads to a new configuration of the constitutive relations，which are rationally elucidated by the theory of surface elasticity of Gurtin-Murdoch［10-12］.Actually，the surface stresses are related to the surface strains by defining three crucial properties for the surface layer（i.e.，twoLame’s constants plus the residual surface stress）.These parameters are commonly determined by comparing the predicted mechanical responses by the proposed surface energy-based model and those obtained from an appropriate atomistic-based model［13，14］.To date，the surface elasticity model of Gurtin-Murdoch has been widely employed in mechanicalanalysis ofnanowires［15-30］，beam-like nanostructures［31-39］，nanoplates［40-45］，nanotubes［46-51］，and other elasticity problems［52，53］.

The intrinsic propertiesofnanoshafts could be customized by controlling the shape，size，composition，material variation or a combination of these factors.In the present study，the material properties of the nanoshaft are only allowed to vary gradually in the radial direction based on a power-law relation.Such an issue enables us to use the nanoshaft more efficiently for the considered job.For instance，if the outer surface of the nanoshaft will be subjected to a high temperature during its service life，the composition of the material should be decorated such that the material of the outermost surface would have the lowest levels of the coefficients of thermal expansion as well as thermal conductivity.Furthermore，the used materials at the location of occurrence of maximum radial and hoop stresses should have adequate strength such that these maximum values do not exceed the capacity of the material.Such engineered-based smart materials are commonly called functionally graded materials（FGMs）.So far，the in-plane deformation ofrotating disks and plates made-up of FGMs in thermal environments have been extensively studied［54-62］；however，no research work could be found in the literature that committed to the elastic fields ofthermally affected rotating nanoshafts.In the present work，particular attention will be also devoted to this matter of how material variation along the radial direction affects the resultant deformation and stress fields of the nanostructure.

Herein，thermo-elastic governing equations of rotating annular nanoshafts with varying material properties in the radial direction are derived.By developing an analytical approach，the explicit expressions of radial displacement，hoop，and radial stresses are obtained accounting for the surface energy effect.For both fixed-free and free-free conditions，the surface effect is introduced into the boundary conditions.In a special case，the obtained results are verified with those of another work and a reasonably good agreement is reported.Subsequently，the influences of the power-law index，temperature of the surrounding medium，angular velocity，nanoshaft’s outer radius，and the surface energy on the resulted thermo-elastic field are explained and discussed in some detail.This work can be considered as a pivotal step towards technical design and fabrication of thermally affected nano-scaled rotors or nanomachines with rotating tube-like elements or hollow nanowires.

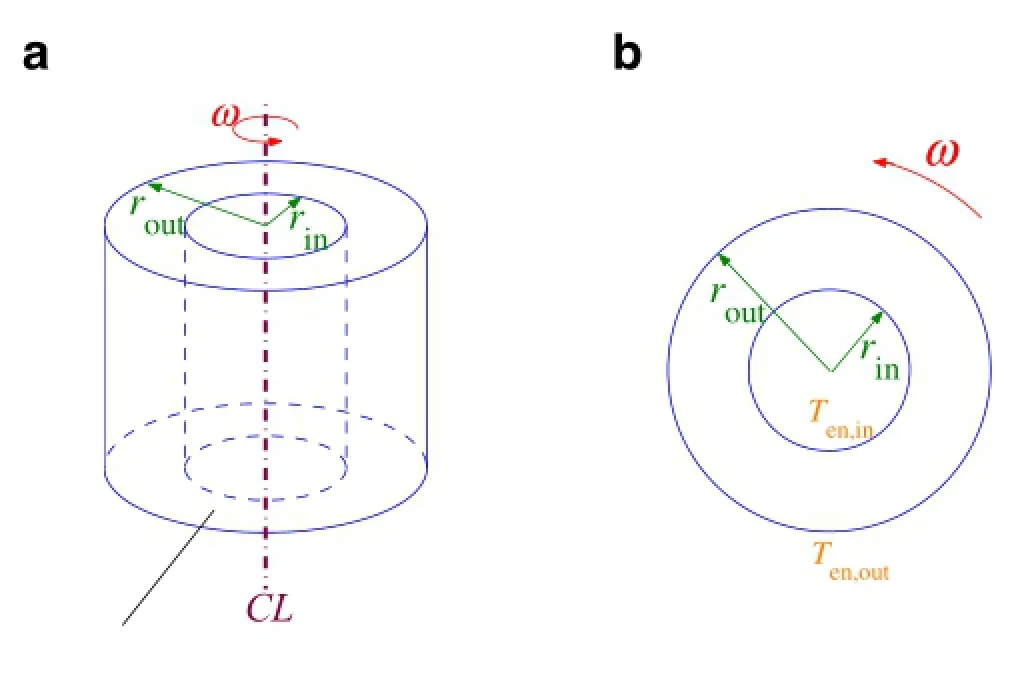
Fig.1 a A rotating circular hollow nanoshaft with varying material properties in a thermal environment.b Top view of the nanostructure

2　Statement of the problem and assumptions of the proposed model

2.1Definition of the problem

Consider a lengthy hollow nanoshaft rotating with a constant angular velocity ω about its revolutionary axis in a thermal environment as demonstrated in Fig.1a.The inner and outer radii of the nanoshaft are rinand rout，respectively，and the temperature of the moving fluid in contact with its inner and outer surface in order are denoted by Ten，inand Ten，out.The centrifugal force plus the temperature gradient would result in stresses within the nanoshaft，which endangerthe performance ofthe rotating nanostructure.Therefore，evaluation ofsuch stress fields and identification ofthe influential factors would be very helpful to designers.One way to optimally design these nanostructures is to use materials whose properties vary gradually in the radial direction. Such an option enables us to examine mechanical response of rotating nanoshafts for a wide range of variation of material properties.By assessing the thermo-elastic fields of the nanostructure，those caseswhich lead to lowerdisplacements and stresses are identified.

2.2Major assumptions of the proposed model

The following assumptionsare made in modeling ofthe problem at hand:

（1）The deformation of the nanostructure in the context of linear elastic behavior is of interest.In extreme conditions（i.e.，rotating nanoshaft with high angular velocity acted upon by high environmental temperature fields），some regions of the nanostructure may become plastic. The location and area of this zone relies on the thermal and elastic boundary conditions，distribution of material properties，angular velocity，and thermal change.Additionally，the nonlinear mechanical response of the rotating nanoshaftisnotofconcern in thisstudy.Fornonlinear problems，special numerical techniques should be employed to determine the thermo-elastic field of the rotating nanoshaft.

（2）The angular velocity of the nanoshaft as well as the temperature of the fluid at the vicinity of the nanoshaft’s surface gradually increase until reach their maximum values and then remain unchanged.For such a scenario，steady-state analysis of the problem based on these extreme values would be satisfactory.The need for dynamic analysis intensifies if these factors vary suddenly in a short time-interval（i.e.，thermal or angular velocity shock）.

（3）The properties of the constitutive materials radially vary by the following power-law relations:

where E（r），αT（r），k（r），and ρ（r）denote the Young’s modulus，thermal expansion coefficient，thermal conductivity coefficient，and density ofthe materials，respectively.Throughout this paper，the parameters whose subscripts are specified by in and out in order are associated with the inner and outer surfaces of the nanoshaft.

（4）The constitutive materials of the nanoshaft behave like isotropic materials.In other words，the mechanical behaviorofthe materialsin the radialand hoop directions are the same.In regard to this fact plus the axisymmetric condition ofboth the temperature field ofthe surrounding environment and the exerted centrifugal force，the threedimensional problem is reduced to a two-dimensional one（e.g.，an axisymmetric nanoshaft；see Fig.1b）.

3　Thermal analysis of the rotating nanoshaft

3.1Heat conduction equation and boundary conditions

Due to axisymmetric conditions of the rotating nanoshaft with varying material properties along the radial direction，the steady governing equation of the thermal field within the nanostructure reads:

where d is the differential sign，and T=T（r）is the temperature field of the nanoshaft that should be determined.Since the inner and outer surfaces of the nanoshaft have been in contact with the thermal environment，the heat can be conducted from the surrounding media into the nanoshaft by considering the following conditions:

where hinand houtin order denote the heat transfer coefficients of the inner and outer surfaces of the rotating nanoshaft.By introducing the dimensionless spatial parameterthe dimensionless governing equation and its boundary conditions are expressed by:

where the constant coefficientsare determined by satisfying the boundary conditions in Eq.（4b）and（4c）. As a result，the temperature field of the rotating nanoshaft is derived as

4　Thermo-elastic field analysis of the rotating nanoshaft

4.1Governing equations

Based on the second and fourth assumptions，the only governing equation in terms of stresses and exerted body force is expressed by:

where σrrand σθθare the radial and hoop stresses within the rotating nanoshaft，ar=rω2is the centrifugal acceleration，andωisthe angularvelocity ofthe rotating nanoshaft.In view of the first and fourth assumptions，the constitutive relations in the case of plane-stress condition would be:

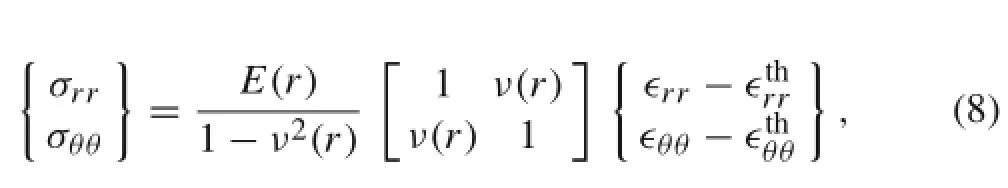
where ν（r）is the Poisson’s ratio，ϵrrand ϵθθin order are the total radial and hoop strains，and finally，are， respectively，the thermalradialand hoop strains.By recalling the first and fourth assumptions，these strains are given by

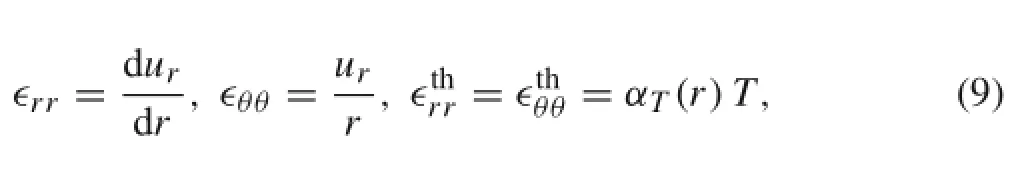
where ur=ur（r）represents the radial displacement field. By substituting the strains in Eq.（9）into（8），and then by introducing the resulting expressions to Eq.（7），the governing as a function of the rotating nanoshaft in thermal environments as a function of radial displacement is derived as

Now assume thatthe Poisson’s ratio would be constantin the whole domain of the nanoshaft.Therefore，Eq.（10）can be simplified to:

In order to investigate the problem in a more general context，the following dimensionless parameters are taken into account:

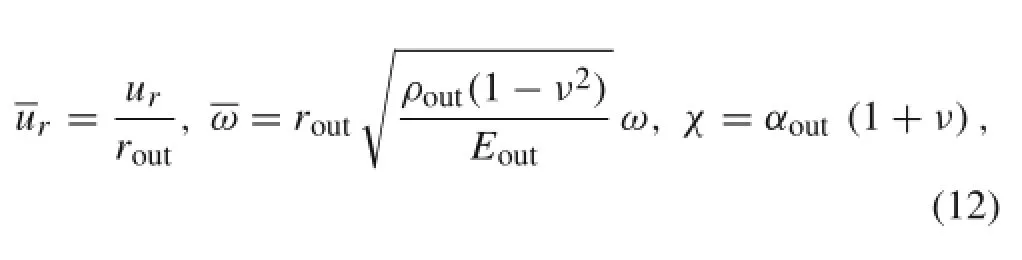
by introducing Eq.（12）to（11）in view of Eq.（1），the dimensionless governing equation is obtained as

finally，by substituting Eq.（5）into（13），the differentialequation of the radial displacement is obtainable as follows

Equation（14）is a second-order linear ODE whose solution can be readily sought as

by substituting Eq.（16）into（18），the explicit expressions of the hoop and radial stresses as a function of unknown coefficients are derived:

4.2Imposition of the non-classical boundary conditions

4.2.1An introduction to the Gurtin-Murdoch model

According to this theory，when the dimensions of the solid body are in the range of several nanometers to several tens of nanometers，the effect of the surface strain energy in the total strain energy of the nanostructure becomes important.Thereby，this advanced theory of elasticity suggests to decompose the whole elastic body into the bulk zone and the surface layer.The surface is a very thin layer with negligible thickness，which has been tightly attached to its underlying bulk zone.Hence，the displacements of the surface layer are identical to those of the bulk at the vicinity of the interface layer.Based on the Gurtin-Murdoch model［10-12］，the constitutive relations of the surface layer with a constant radius are stated by: where∂denotes the partial differential sign，in order are the surface strains and stresses，μsand λsare the surface Lamé’s constants，αs，Tis the thermal coefficient expansion ofthe surface layer，τ0isthe residualsurface stress underunconstrained conditions，uαisthe displacementalong the α direction，and δαβis the Kronecker delta tensor.

Recently，ithas been pointed outthatthe reference and the currentconfigurations ofnanostructures（forboth the surface and the bulk）should be discriminated，even in the case of small deformations［63，64］.Such a fact is mainly attributed to the existence of residual surface stress.The importance of considering the out-of-plane terms of surface deformation gradients for curved and rotated surfaces in the Eulerian description was also emphasized.Without making the problemso complex from the theoreticalmechanicspointofview，the fixed-free and free-free boundary conditions based on the Gurtin-Murdoch elasticity theory of surface are explained in the following parts.

4.2.2Fixed-free boundary conditions

In this boundary condition，the innersurface ofthe nanoshaft is prohibited from any radial displacement（i.e.，ur（rin）=0）and the exterior points of the outer surface layer are traction free.By considering an infinitesimal element of the outer surface layer，and neglecting the radial centrifugal force of the surface，the requirement of static equilibrium leads to:

As a result，the boundary conditions of a fixed-free rotating nanoshaft take the following form:

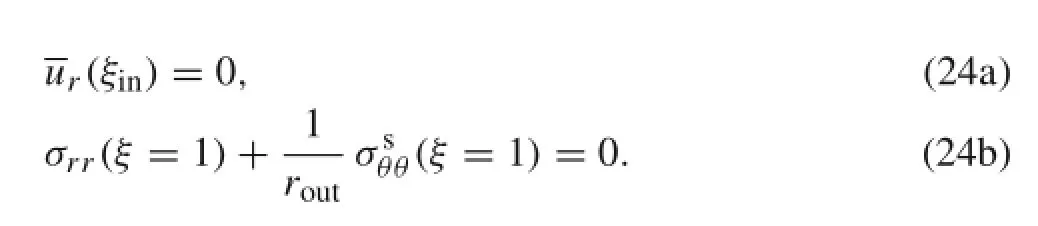
By introducing the radial displacement and stress fields of the bulk and the surface layer to the conditions in Eq.（24a）and（24b），one can arrive at:

By solving the set of two linear equations in Eq.（25a）and（25b），the coefficientswill be readily determined.

4.2.3Free-free boundary conditions

This boundary condition states that those points of the inner and outersurfaces ofthe nanoshaft，which are in contactwith the surrounding environment，are traction free.Therefore，the boundary condition of the outer surface is identical to that given in Eq.（22）.In order to obtain the boundary condition of the inner surface，an infinitesimal element of the surface layer is considered and the Newton’s second law is applied. By neglecting the centrifugal force of the surface layer，we would arrive at the following relation:

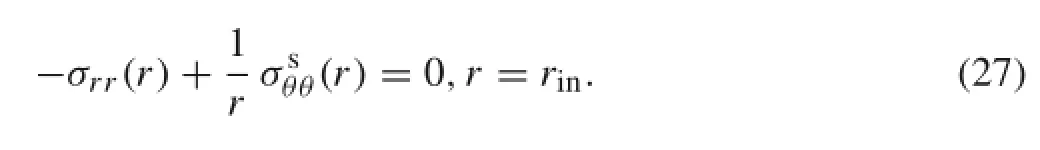
Finally，the conditions pertinent to the free-free rotating nanoshaft can be expressed by:

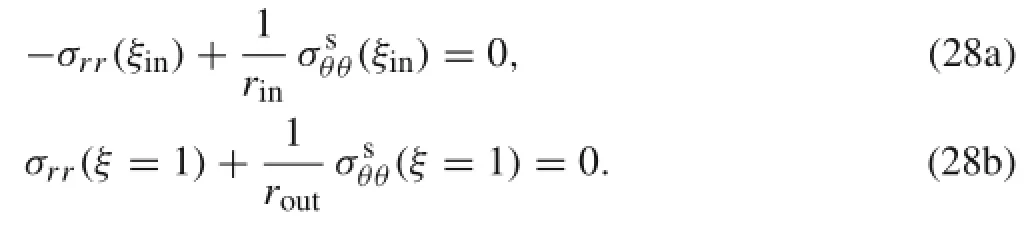
By enforcing the recent non-classical boundary conditions to the general form of stress fields in Eqs.（19）and（23），it is obtained:

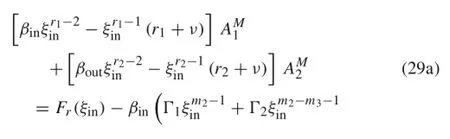
Finally，by solving the set of equations in Eq.（29a）and（29b）for AM1and AM2，the thermo-elastic field ofthe rotating nanoshaft with free-free boundary condition accounting for the surface energy is determined.

5　Results and discussion

5.1Verification of the obtained results with those of other works

In order to study the accuracy of the suggested model，the obtained results are checked with those of another work in a specialcase.Considera macro-scale rotating hollow circular disk with ω=600 rad/s and rin=0.2rout，which is subjected to a thermal field with Ten，in=0 and Ten，out=1000◦C.All materials properties vary along the radial direction in the form:［.］= ［.］out（r/rout）mwhere［.］stands for the density，coefficient of thermal expansion，thermal conductivity coefficient，or the Young’s modulus，and ρout=2700 kg/m3，ν=0.3，kout=209 W/（m◦C），αT，out=23×10-6◦C-1，and Eout=70 GPa.Itshould be noted that Peng and Li［62］studied the thermo-elastic field of such a structure by proposing a numerical model based on the Fredholm integral equation. For three levels of the power-law index（i.e.，m=-0.5，0，and 0.5），the predicted dimensionless radial displacement，the hoop stress，and the radial stress of the present study as well as those of Peng and Li［62］are provided in Table 1 for the case of free-free boundary condition.The dimensionless thermo-elastic field is defined by:

As itis seen in Table 1，the proposed model can successfully capture the results of the model of Peng and Li［62］for all levels of the power-law index.

Table 1 Verification of the predicted thermo-elasic fields by the proposed model for a rotating macro-scale disk in a thermal environment and those of Peng and Li［62］

5.2Parametric studies

Consider a rotating nanoshaft in a thermal environment whose outer surface has been made from aluminum［100］with the following data［65-67］:ρout=2700 kg/m3，ν=0.3，k out=209 W/（m◦C），αT，out=23.1×10-6◦C-1，E out= 70 GPa，τ0，out=0.5689 N/m，λ0，out=3.4939 N/m，and μ0，out=-5.4251 N/m.The thermo-mechanical material properties of the nanoshaft as well as those of the inner surface are determined based on the introduced power-law relation for the special case of m1=m2=m3=m4=m. In the absence ofdata on the coefficientofthermalexpansion of the surface layers，the values of these parameters are set equal to zero.To examine the resulting elastic field within the nanostructure，the following dimensionless quantities are taken into account:

where rout，0，Ten，out，0，andω0in orderare setequalto 10 nm，1000◦C，and 1000 rad/s，exceptothervalues are clearly specified for these factors.

5.2.1Influence of the environment’s temperature

In an interesting study，the role of the temperature of the environments as well as the surface energy effect on the thermo-elastic field within the rotating nanoshaft is investigated.In Fig.2a and b，the plots of the radial displacement field，radial and hoop stress fields of the fixed-free and freefree nanoshafts have been demonstrated for four levels of the environment’s temperature（i.e.，Ten，out=60◦C，120◦C，240◦C，and 480◦C）.The results are provided fora nanoshaft that rotates with ω=1000 rad/s and its material properties varies spatially accounting for m=2.Forboth fixed-free and free-free boundary conditions，the predicted radial displacements and radialstresses accounting forthe surface effectare overestimated by those obtained withoutconsideration ofthe surface effect.Generally，by an increase ofthe temperature of the outside environment，the relative discrepancies between the predicted radialdisplacementand radialstress by considering the surface energy effectand those withoutconsidering the surface energy effect would reduce.In both cases of the fixed-free and free-free conditions，the predicted maximum values of hoop stresses by consideration of the surface effect are commonly greaterthan the maximum hoop stresses without consideration of the surface effect.

Fig.2 Thermo-elastic fields for various levels of the environment’s temperature.a Fixed-free.b Free-free.open square Ten，out=60◦C，open circle Ten，out=120◦C，open triangle Ten，out=240◦C，inverted triangle Ten，out=480◦C；dashed line without surface effect，line with surface effect；ω=1000 rad/s，m=2

Specifically，we are also interested in examining the role of the temperature of the surrounding environment on the maximum elastic fields of the rotating nanoshafts accounting for the surface energy effect.In Fig.3a and b，the plots of the maximum absolute values of the thermo-elastic fields within fixed-free and free-free rotating nanoshafts as a function of the temperature are provided.Based on the classical continuum theory，the predicted maximum thermo-elastic fields of the nanoshaft for both fixed-free and free-free conditions would linearly magnify as the temperature of the surrounding environment increases.Nevertheless，such a fact does not hold true exactly for the maximum thermo-elastic fields obtained by consideration of the surface effect.For instance，in the case ofthe fixed-free condition，a closerscrutiny ofthe plots of the maximum absolute value of the elastic fields as a function of the temperature shows that the maximum radial displacement by considering the surface energy effect would lessen nonlinearly with the temperature up to≈180◦C.For temperatures greater than this value，the maximum radial displacement would linearly magnify with temperature.Up to Ten，out≈77◦C，the predicted maximum radial displacements by considering the surface effect are higher than those without consideration of the surface energy effect.However，for Ten，out＞77◦C，those radial displacements predicted by the classical continuum theory are larger than those obtained by consideration of the surface effect.

It should be emphasized that the residual surface stress under unrestrained conditions will cause a residual stress field within the nanoshaft even in the absence of the externally applied thermo-mechanical loads［see Eqs.（25）and（29）］.In fact，the residual stress field is generated within the nanostructure atthe time ofcreation ofthe surface layer.Ifthe generated stresses within the nanoshaft due to only thermomechanical loads would be of concern，one can consider τ0=0.In such a case，the plotted results in Fig.2a and b are reproduced as demonstrated in Fig.4a and b.These figures display thatthe thermo-elastic fields ofthe nanoshaftby consideration ofthe surface effectapproach to those predicted by the classical continuum theory as the residual surface stress vanishes.Such a fact is more apparent in the case of the fixed-free boundary condition.According to Fig.4a and b，the role ofthe surface energy effecton the radialdeformation of the nanoshaft would lessen as one approaches the outer surface of the nanoshaft.In fixed-free rotating nanoshafts，in the absence of the residual surface stress，the relative discrepancies between the radial stresses by considering the surface effect and those of without consideration of the surface effect would increase as one approaches to the outer surface of the nanoshaft.In the free-free boundary conditionwith τ0=0，the maximum of such relative discrepancies is observed atthe innersurface ofthe nanoshaft.Furtherexplorations indicate that the maximum absolute values of both predicted thermo-elastic fields with and without consideration of the surface effect would linearly grow in terms of the temperature.In the case of the fixed-free condition，there exists a negligible discrepancy between the above-mentioned thermo-elastic fields.In free-free rotating nanoshafts，the maximum radial displacements accounting for the surface effect are generally greater than those predicted based on without considering the surface effect；however，the predicted maximum values of both radial and hoop stresses by considering the surface effect are commonly lower than those obtained without consideration of the surface energy effect.

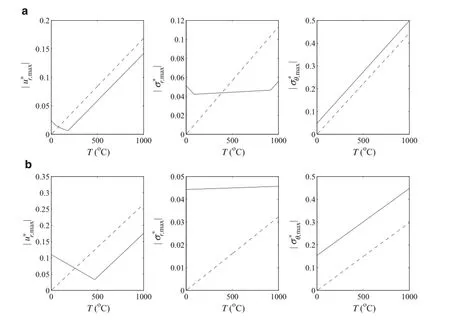
Fig.3 Maximum absolute values of thermo-elastic fields as a function of the environment’s temperature.a Fixed-free.b Free-free.dashed line without surface effect，line with surface effect；ω=1000 rad/s，m=2

5.2.2Influence of the angular velocity

Equally important is to determine the role of the angular velocity on the resulting thermo-elastic fieldswithin the rotating nanoshafts.For this purpose，the graphs of the radial displacement，radial stress，and hoop stress fields for four levels of the angular velocity of the fixed-free and free-free nanoshafts are presented in Fig.5a and b.The plotted results are provided fora nanoshaftwith rin=10 nm，rout=100 nm，and m=0.5 which are subjected to:T en，in=T en，out=0◦C. For both fixed-free and free-free conditions，the elastic field of the nanoshaft would be magnified as the angular velocity of the nanoshaft increases.In the case of the fixed-free boundary condition for all considered angular velocities，the maximum values of the radial displacement，radial stress，and hoop stress fields occur at r≈89.83，10，and 50.05 nm，respectively.However，in the case of the free-free condition，these maximum values in order take place at r≈88.75，41.05，and 10 nm.Further scrutiny of the plotted results reveals thatthe maximum elastic fields ofboth fixed-free and free-free nanoshaftsas a function ofthe angularvelocity vary in a parabolic manner.In both fixed-free and free-free boundary conditions，there exist negligible discrepancies between the predicted elastic fields by consideration of the surface energy effect and those obtained without considering the surface effect.Generally，such small discrepancies for rotating nanoshafts with free-free surfaces are more apparent. In the case of fixed-free rotating nanoshafts，such relative discrepancies would be magnified as one goes from the inner surface to the outer surface.It implies that the surface energy effecthas the mostinfluence on the elastic field ofthe outer surface.Nevertheless，in the case of free-free rotatingnanoshafts，the above-mentioned discrepancies would commonly lessen as one moves from the inner surface to the outer one.

Fig.4 Thermo-elastic fields for various levels of the environment’s temperature.a Fixed-free.b Free-free.open square Ten，out=60◦C，open circle Ten，out=120◦C，open triangle Ten，out=240◦C，inverted triangle Ten，out=480◦C；dashed line without surface effect，line with surface effect；τ0=0，ω=1000 rad/s，m=2

5.2.3Effect of the power-law index

Variation ofthe materialpropertieson the thermo-elastic field ofthe rotating nanoshaftsshould be carefully realized.To fulfill such a crucial task，the plots of the radial displacement，radial stress，and hoop stress within the nanoshaft for four levels of the power-law index（i.e.，m=-1.5，-0.5，0.5，and 1.5）have been demonstrated in Fig.6a and b.These plots are given for both fixed-free and free-free rotating nanoshafts with ω=1000 rad/s，Ten，out=1000◦C，and τ0=0.According to these figures，the surface energy effect has a very trivial effect on the thermo-elastic field of the fixed-free rotating nanoshafts.In fact，the plotted results from considering the surface effect and those without consideration of the surface effect are fairly indistinguishable.For fixed-free rotating nanoshafts，a close survey of the obtained results indicates that the relative discrepancies between the elastic fields by consideration of the surface effect and those without considering the surface effect would commonly grow as the power-law index increases.For radial displacements，such a fact is more obvious for the regions near to the inner surface of the rotating nanoshaft.However，for radial stress fields，the above-mentioned discrepancies are more apparent at the regions close to the outer surface.A brief study of the demonstrated results in Fig.6a and b shows that the relative discrepancies between the elastic fields accounting for the surface effect and those without considering the surface effect in the case of free-free condition are more obvious with respect to those of the fixed-free boundary condition.According to Fig.6，for free-free rotating nanoshafts，the maximum values of radial displacements and hoop stresses，respectively，occur at the outer surface and the inner surface of the nanoshaft.A detailed study of the predicted results reveals that the location of the maximumradialstressapproximately varieslinearly in the interval［rin+0.235（rout-rin），rin+0.557（rout-rin）］asthe power-law index increases from-2 up to 2.For such a boundary condition，the maximum radial displacement，radial stress，and hoop stress would generally reduce as the power-law index increases.A careful study of the plotted results in Fig.6bshows that the relative discrepancies between the radial displacementsaccounting forthe surface energy effectand those predicted without consideration of the surface effect would generally increase as the power-law index increases.Additionally，the relative discrepancies between the radial stress fields by considering the surface effect and those without considering the surface effect would commonly magnify at the zones near to the inner surface and generally reduce at the zones close to the outer surface of the rotating nanoshaft. The rate of the magnification is more apparent with respect to the rate of the reduction.It indicates that the variation of the power-law index has the most influence on the abovementioned discrepancies for the inner surface of the rotating nanoshafts.

Fig.5 Thermo-elastic field for various levels of the angular velocity.a Fixed-free.b Free-free.open square　ω=400 rad/s，open circle ω=800◦C，open triangle ω=1600◦C，inverted triangle ω=2000 rad/s；dashed line without surface effect，line with surface effect；τ0=0，rin=10 nm，rout=100 nm，m=0.5，Ten，in=Ten，out=0◦C；ω0=2000 rad/s，rout，0=100 nm，Ten，out，0=0◦C

5.2.4Influence of the outer radius

The effect of the outer radius of the thermally affected rotating nanoshaft on the generated thermo-elastic field is the subject of another crucial parametric study that should be examined methodically.To this end，the plots of the radial displacements，radial stresses，and hoop stresses of the rotating nanoshaft for various values of the outer radius for both fixed-free and free-free conditions have been demonstrated in Fig.7a and b.The obtained results are given for a rotating nanoshaft with ω=1000 rad/s，Ten，out=400◦C，and m=2. In the case of the fixed-free boundary condition，the predicted radial displacements would magnify by an increase of the outermost radius of the nanoshaft；however，the radial and hoop stresses of each point of the rotating nanoshaft would commonly lessen as the outer radius increases.In the case of the free-free boundary condition，the obtained radial displacements with and without consideration of the surface effect would increase as the outer radius of the rotating nanoshaft increases.Additionally，the radial stresses of the regions close to the outersurface generally magnify asthe outer radius of the nanoshaft increases.Nevertheless，those ofthe zones adjacentto the innersurface would increase with the outer radius up to a certain value of the outer radius.For outer radii greater than this certain value，the radial stresses would decrease as the outer radius increases.Concerning the trend of the hoop stress in terms of the outer radius，the hoop stress field of the rotating nanoshaft as a function of dimensionless coordinate parameter ζ would commonly lessen with the outer radius.As a general result，the role ofthe surface energy effect on the thermo-elastic fields of the free-free nanoshafts is more obvious with respect to those of the fixed-free nanoshafts.

Fig.6 Thermo-elastic fields for various levels of the power-law index.a Fixed-free.b Free-free.open square m=-1.5，open circle m=-0.5，open triangle m=0.5，inverted triangle m=1.5；dashed line withoutsurface effect，line with surface effect；τ0=0，ω=1000 rad/s，T en，out=1000◦C

We are also interested in how variation of the outer radius of the rotating nanoshaft would affect its size-dependent thermo-elastic field.To achieve such a crucial goal，the plotted results in Fig.7a and b are reanalyzed，and the discrepancies between the dashed lines and solid lines are carefully reported.Regarding the fixed-free rotating nanoshafts，in the case of rout/rin=2，the predicted radial displacements and radialstresses by consideration ofthe surface effect are commonly overestimated by those obtained without consideration of the surface effect.However，for rout/rin≥4，the predicted radial displacements as well as radial stresses accounting for the surface effect are generally underestimated by those withoutconsideration ofthe surface effect.For all considered values of rout/rin，the relative discrepancies between the radialdisplacements（radialstresses）considering the surface effect and those predicted without considering the surface effect would generally reduce（increase）by approaching to the outer surface of the rotating nanoshaft.Concerning the free-free rotating nanoshafts，the surface energy effect has the most influence on the radial displacements and the radial stresses of the inner surface of the nanoshaft.Furthermore，by increasing the outer radius of the nanoshaft，the relative discrepancies between the radial displacements（or radial stresses）of the regions close to the inner surface accounting for the surface effect and those without consideration of the surface effect would usually magnify.However，such relative discrepancieswould commonly reduce at the points near to the outer surface of the rotating nanoshaft.The maximum hoop stresses of both fixed-free and free-free nanoshafts would lessen as the outer radius of the nanoshaft increases.Generally，the maximum values ofthe hoop stress fields ofthe rotating nanoshaftfrom consideration ofthe surface effectare overestimated by those obtained without considering the surface effect.Additionally，the relative discrepancies between the maximum hoop stresses accounting for the surface energy effect and those without consideration of the surface energy effect would commonly grow as the outer radius of the rotating nanoshaft increases.

Fig.7 Thermo-elastic fields for various levels of the outer radius of the rotating nanoshaft.a Fixed-free.b Free-free.open square rout=2 rin，open circle rout=4rin，open triangle rout=6rin，inverted triangle rout=10rin；dashed line without surface effect，line with surface effect；τ0=0，m=2，ω=ω0=1000 rad/s，T en，out=400◦C，T en，out，0=400◦C，r out，0=10r in

6　Conclusions

Thermo-elastic fields of rotating nanoshafts with varying material properties in thermal environments are of concern accounting for the surface energy effect.By considering a power-law relation for variation of the material properties of the nanoshaft along the radial direction，the analytical expressions of the thermal field as well as the displacements and stresses within the nanoshaft are obtained.The problem is carefully studied for both fixed-free and free-free boundary conditions.In a special case，the obtained results are verified with those of another work and a reasonably good agreement is achieved.Subsequently，the roles of the environment’s temperature，angular velocity，variation of the material properties，outer radius of the nanoshaft，and surface energy effect on the thermo-elastic fields within the nanoshafts are addressed and discussed in some detail.

The obtained results from the present work would be very useful in optimal design and nano-engineering of rotating nanoshafts.The proposed model can be easily applied to thermally affected rotating core-shell nanowires，which are of great interest to the community of nanomechanics.Additionally，the quasi-static response and vibrations of rotating nanoplates in thermal environments as well as their possible dynamic instabilities have not been investigated carefully. These interesting explorationsforfinding the dynamic behaviorofsuch nanostructures would increase ourknowledge and would lead to the design and production of more efficient nanorotors.

1.Maruo，S.，Ikuta，K.，Korogi，H.:Submicron manipulation tools driven by light in a liquid.Appl.Phys.Lett.82，133-135（2003）

2.Khan，M.，Sood，A.K.，Deepak，F.L.，etal.:Nanorotors using asymmetric inorganic nanorods in an optical trap.Nanotechnology 17，S287（2006）

3.Stockman，M.I.，Li，K.，Brasselet，S.，et al.:Octupolar metal nanoparticles as optically driven，coherently controlled nanorotors. Chem.Phys.Lett.433，130-135（2006）

4.Tong，L.，Miljkovic，V.D.，Käll，M.:Alignment，rotation，and spinning of single plasmonic nanoparticles and nanowires using polarization dependent optical forces.Nano Lett.10，268-273（2009）

5.Jones，P.H.，Palmisano，F.，Bonaccorso，F.，etal.:Rotation detection in light-driven nanorotors.ACS Nano 3，3077-3084（2009）

6.Maruo，S.，Inoue，H.:Optically driven micropump produced by three-dimensional two-photon microfabrication.Appl.Phys.Lett. 89，144101（2006）

7.Lin，C.L.，Vitrant，G.，Bouriau，M.，et al.:Optically driven Archimedes micro-screws for micropump application.Opt.Exp. 19，8267-8276（2011）

8.Lin，C.L.，Wang，I.，Dollet，B.，et al.:Velocimetry microsensors driven by linearly polarized optical tweezers.Opt.Lett.31，329-331（2006）

9.Bonin，K.，Kourmanov，B.，Walker，T.:Light torque nanocontrol，nanomotors and nanorockers.Opt.Exp.10，984-989（2002）

10.Gurtin，M.E.，Murdoch，A.I.:A continuum theory of elastic material surfaces.Arch.Ration.Mech.Anal.57，291-323（1975）

11.Gurtin，M.E.，Murdoch，A.I.:Effectofsurface stress on wave propagation in solids.J.Appl.Phys.47，4414-4421（1976）

12.Gurtin，M.E.，Murdoch，A.I.:Surface stress in solids.Int.J.Solids Struct.14，431-440（1978）

13.Shenoy，V.B.:Size-dependent rigidities of nanosized torsional elements.Int.J.Solids Struct.39，4039-4052（2002）

14.Miller，R.E.，Shenoy，V.B.:Size-dependent elastic properties of nanosized structural elements.Nanotechnology 11，139-147（2000）

15.He，J.，Lilley，C.M.:Surface effect on the elastic behavior of static bending nanowires.Nano Lett.8，1798-1802（2008）

16.He，J.，Lilley，C.M.:Surface stress effect on bending resonance of nanowires with different boundary conditions.Appl.Phys.Lett. 93，263108（2008）

17.Gao，F.，Cheng，Q.，Luo，J.:Mechanics of nanowire buckling on elastomeric substrates with consideration of surface stress effects. Phys.E 64，72-77（2014）

18.Kiani，K.:Forced vibrations of a current-carrying nanowire in a longitudinal magnetic field accounting for both surface energy and size effects.Phys.E 63，27-35（2014）

19.Kiani，K.:Surface effect on free transverse vibration and dynamic instability of current-carrying nanowires in the presence of a longitudinal magnetic field.Phys.Lett.A 378，1834-1840（2014）

20.Kiani，K.:Column buckling of magnetically affected nanowires carrying electric current.J.Phys.Chem.Solids83，140-151（2015）

21.Kiani，K.:Stability and vibrations of doubly parallel currentcarrying nanowires immersed in a longitudinal magnetic field. Phys.Lett.A 379，348-360（2015）

22.Kiani，K.:Axial buckling analysis of a slender current-carrying nanowire acted upon by a longitudinal magnetic field.J.Phys.D Appl.Phys.48，245302（2015）

23.Kiani，K.:Vibrations and instability of pretensioned currentcarrying nanowires acted upon by a suddenly applied threedimensional magnetic field.Mater.Chem.Phys.162，531-541（2015）

24.Song，F.，Huang，G.L.:Modeling of surface stress effects on bending behavior of nanowires:Incremental deformation theory.Phys. Lett.A 373，3969-3973（2009）

25.Wang，Y.，Wang，Z.Q.，Lv，J.G.:Size-dependent thermal buckling ofheated nanowires with ends axially restrained.Phys.Lett.A 378，899-903（2014）

26.Liu，J.L.，Mei，Y.，Xia，R.，et al.:Large displacement of a static bending nanowire with surface effects.Phys.E 44，2050-2055（2012）

27.Wang，G.F.，Feng，X.Q.:Surface effects on buckling of nanowires under uniaxial compression.Appl.Phys.Lett.94，141913（2009）

28.Wang，G.F.，Feng，X.Q.:Timoshenko beam modelforbuckling and vibration of nanowires with surface effects.J.Phys.D Appl.Phys. 42，155411（2009）

29.Park，H.S.，Klein，P.A.:Surface stress effects on the resonant properties of metal nanowires:the importance of finite deformation kinematics and the impact of the residual surface stress.J.Mech. Phys.Solids 56，3144-3166（2008）

30.Gordon，M.J.，Baron，T.，Dhalluin，F.，etal.:Size effectsin mechanical deformation and fracture of cantilevered silicon nanowires. Nano Lett.9，525-529（2009）

31.Guo，J.G.，Zhao，Y.P.:The size-dependent bending elastic propertiesofnanobeamswith surfaceeffects.Nanotechnology 18，295701（2007）

32.Fu，Y.，Zhang，J.:Size-dependentpull-in phenomena in electrically actuated nanobeams incorporating surface energies.Appl.Math. Model.35，941-951（2011）

33.On，B.B.，Altus，E.，Tadmor，E.B.:Surface effects in non-uniform nanobeams:continuumvs.atomistic modeling.Int.J.SolidsStruct. 47，1243-1252（2010）

34.Gheshlaghi，B.，Hasheminejad，S.M.:Surface effects on nonlinear free vibration of nanobeams.Compos.Part B Eng.42，934-937（2011）

35.Fu，Y.，Zhang，J.，Jiang，Y.:Influences of the surface energies on the nonlinear static and dynamic behaviors of nanobeams.Phys.E 42，2268-2273（2010）

36.Hasheminejad，S.M.，Gheshlaghi，B.，Mirzaei，Y.，etal.:Free transverse vibrations of cracked nanobeams with surface effects.Thin Solid Films 519，2477-2482（2011）

37.Malekzadeh，P.，Shojaee，M.:Surface and nonlocal effects on the nonlinear free vibration of non-uniform nanobeams.Compos.Part B Eng.52，84-92（2013）

38.Eltaher，M.A.，Mahmoud，F.F.，Assie，A.E.，et al.:Coupling effects ofnonlocaland surface energy on vibration analysisofnanobeams. Appl.Math.Comp.224，760-774（2013）

39.Hosseini-Hashemi，S.，Nazemnezhad，R.:An analytical study on the nonlinear free vibration of functionally graded nanobeams incorporating surface effects.Compos.Part B Eng.52，199-206（2013）

40.Ansari，R.，Sahmani，S.:Surface stress effects on the free vibration behavior of nanoplates.Int.J.Eng.Sci.49，1204-1215（2011）

41.Zang，J.，Fang，B.，Zhang，Y.W.，et al.:Longitudinal wave propagation in a piezoelectric nanoplate considering surface effects and nonlocal elasticity theory.Phys.E 63，147-150（2014）

42.Asemi，S.R.，Farajpour，A.:Thermo-electro-mechanical vibration of coupled piezoelectric-nanoplate systems under non-uniform voltage distribution embedded in Pasternak elastic medium.Curr. Appl.Phys.14，814-832（2014）

43.Mouloodi，S.，Khojasteh，J.，Salehi，M.，et al.:Size dependent free vibration analysis of multicrystalline nanoplates by considering surface effects as well as interface region.Int.J.Mech.Sci.85，160-167（2014）

44.Ansari，R.，Ashrafi，M.A.，Pourashraf，T.，etal.:Vibration and buckling characteristics of functionally graded nanoplates subjected to thermal loading based on surface elasticity theory.Acta Astronaut. 109，42-51（2015）

45.Zhang，L.L.，Liu，J.X.，Fang，X.Q.，et al.:Effects of surface piezoelectricity and nonlocal scale on wave propagation in piezoelectric nanoplates.Eur.J.Mech.A Solid 46，22-29（2014）

46.Wang，L.:Vibration analysis of fluid-conveying nanotubes with consideration of surface effects.Phys.E 43，437-439（2010）

47.Lei，X.W.，Natsuki，T.，Shi，J.X.，et al.:Surface effects on the vibrationalfrequency ofdouble-walled carbon nanotubesusing the nonlocalTimoshenko beam model.Compos.PartBEng.43，64-69（2012）

48.Lee，H.L.，Chang，W.J.:Surface effects on frequency analysis of nanotubes using nonlocal Timoshenko beam theory.J.Appl.Phys. 108，093503（2010）

49.Farshi，B.，Assadi，A.，Alinia-ziazi，A.:Frequency analysis of nanotubes with consideration of surface effects.Appl.Phys.Lett.96，093105（2010）

50.Arani，A.G.，Roudbari，M.A.:Nonlocal piezoelastic surface effect on the vibration ofvisco-Pasternak coupled boron nitride nanotubesystem under a moving nanoparticle.Thin Solid Films 542，232-241（2013）

51.Peng，X.L.，Huang，G.Y.:Elastic vibrations of a cylindrical nanotube with the effect of surface stress and surface inertia.Phys.E 54，98-102（2013）

52.Ru，C.Q.:Simple geometrical explanation of Gurtin-Murdoch model of surface elasticity with clarification of its related versions. Sci.China Phys.Mech.Astron.53，536-544（2010）

53.Kim，C.I.，Schiavone，P.，Ru，C.Q.:Analysis of plane-strain crack problems（mode-Iand mode-II）in thepresence ofsurfaceelasticity. J.Elast.104，397-420（2011）

54.Durodola，J.F.，Attia，O.:Deformation and stresses in functionally graded rotating disks.Compos.Sci.Technol.60，987-995（2000）

55.Bayat，M.，Saleem，M.，Sahari，B.B.，etal.:Analysisoffunctionally graded rotating diskswith variable thickness.Mech.Res.Commun. 35，283-309（2008）

56.Vel，S.S.，Batra，R.C.:Exact solution for thermoelastic deformations of functionally graded thick rectangular plates.AIAA J.40，1421-1433（2002）

57.Horgan，C.O.，Chan，A.M.:The stress response of functionally graded isotropic linearly elastic rotating disks.J.Elast.55，219-230（1999）

58.Nie，G.J.，Batra，R.C.:Stress analysis and material tailoring in isotropic linear thermoelastic incompressible functionally graded rotating disks of variable thickness.Compos.Struct.92，720-729（2010）

59.Singh，S.B.，Ray，S.:Steady-state creep behavior in an isotropic functionally graded material rotating disc of Al-SiC composite. Metall.Mater.Trans.A 32，1679-1685（2001）

60.Shahzamanian，M.M.，Sahari，B.B.，Bayat，M.，etal.:Finite element analysis of thermoelastic contact problem in functionally graded axisymmetric brake disks.Compos.Struct.92，1591-1602（2010）

61.Dong，C.Y.:Three-dimensional free vibration analysis of functionally graded annular plates using the Chebyshev-Ritz method. Mater.Des.29，1518-1525（2008）

62.Peng，X.L.，Li，X.F.:Thermalstressin rotating functionally graded hollow circular disks.Compos.Struct.92，1896-1904（2010）

63.Wang，Z.Q.，Zhao，Y.P.，Huang，Z.P.:The effects of surface tension on the elastic properties of nano structures.Int.J.Eng.Sci.48，140-150（2010）

64.Wang，Z.Q.，Zhao，Y.P.:Thermo-hyperelastic models for nanostructured materials.Sci.China Phys.Mech.Astron.54，948-956（2011）

65.Miller，R.E.，Shenoy，V.B.:Size-dependent elastic properties of nanosized structural elements.Nanotechnology 11，139（2000）

66.Shenoy，V.B.:Atomistic calculations ofelastic properties of metallic fcc crystal surfaces.Phys.Rev.B 71，094104（2005）

67.Liu，C.，Rajapakse，R.K.N.D.，Phani，A.S.:Finite elementmodeling of beams with surface energy effects.J.Appl.Mech.78，031014（2011）

24 October 2015/Revised:23 December 2015/Accepted:4 January 2016/Published online:21 April 2016

©The Chinese Society of Theoretical and Applied Mechanics；Institute of Mechanics，Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016