奇异值分解结合频率切片小波变换的轴承故障提取方法
周福成 唐贵基 王晓龙 廖兴华
(华北电力大学科技学院1,河北 保定 071003;华北电力大学能源动力与机械工程学院2,河北 保定 071003;湖南雁能建设集团有限公司输电工程分公司3,湖南 衡阳 421000)
奇异值分解结合频率切片小波变换的轴承故障提取方法
周福成1唐贵基2王晓龙2廖兴华3
(华北电力大学科技学院1,河北 保定071003;华北电力大学能源动力与机械工程学院2,河北 保定071003;湖南雁能建设集团有限公司输电工程分公司3,湖南 衡阳421000)
针对频率切片小波变换在强背景噪声条件下故障特征识别能力不足的缺点,提出了奇异值分解和频率切片小波变换相结合的故障特征提取方法。首先利用原始信号构造Hankel矩阵,根据奇异值差分谱单边极大值原则确定阶次并进行降噪处理;继而利用频率切片小波对降噪信号进行分析,得到全频带时频图后,对能量集中的时频区域进行细化分析;通过频率切片小波逆变换得到相应的重构信号;最终可以从重构信号的波形图中提取出轴承故障特征频率信息。仿真信号和实测信号分析表明,该方法能够实现滚动轴承运行状态的准确判别,对实际工程应用具有重要意义。
轴承故障诊断特征识别特征提取奇异值分解频率切片小波变换降噪时频分析信号重构
0 引言
轴承是机械设备中支撑轴的重要零部件,其在旋转机械中必不可缺。在实际应用中,受振动传输路径及外界环境噪声等因素的影响,有效提取轴承故障并不容易,为此诸多学者都在寻求行之有效的故障诊断方法[1-2]。时频分析方法通过提取信号时域和频域局部信息,可实现对机械故障的分析和诊断,广泛应用于提取机械轴承非平稳信号。目前常见的时频分析方法主要有Hilbert-Huang变换、小波变换等。Hilbert-Huang变换和小波变换方法各有优缺点,前者对于多频率成分信号有较高的时频分辨率,但分辨率在高频区较低;后者有较高的时间分辨率,但不能根据信号特征选择基函数,分解和重构依赖选定的小波基函数[3]。基于小波变换,Yan等[4-5]提出了频率切片小波变换(frequencyslicewavelettransform,FSWT)理论。通过引入频率切片函数,使传统的傅里叶变换具备时频分析功能。通过对原始信号进行滤波和分割,可有效去除噪声,提取有用信号。相关学者将其移植应用于机械故障诊断领域,如段晨东等[6]利用FSWT来诊断炼油厂齿轮箱摩擦故障,分析并诊断发电机组转子碰摩故障;钟先友等[7]在形态自相关的基础上,利用FSWT进行轴承故障诊断。
虽然基于FSWT的机械故障信号处理方法在实际诊断应用中颇具成效,但经深入研究后发现,在背景噪声干扰较为严重的情况下,FSWT故障特征提取能力仍不够理想。奇异值分解(singularvaluedecomposition,SVD)是一种非线性滤波方法,它能有效去除信号中的噪声分量,在提取故障信号方面具有积极作用[8-10]。为了更有效地提取、分离轴承故障特征,本文提出了SVD降噪和FSWT相结合的故障特征提取方法,并将其运用于滚动轴承故障诊断。仿真和试验数据分析验证了该方法的可靠性。
1 频率切片小波原理
1.1频率切片小波变换
信号f(t)的频率切片小波变换为:
(1)
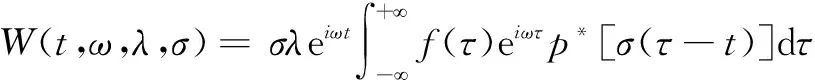
(2)
1.2频率切片小波变换尺度因子的选择
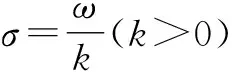
(3)
(4)
根据Heisenberg不确定性原理,采用折中方案估计σ和ω,并在分析信号中,引入频率分辨比率η(η=Δω/ω)和幅值期望响应比率v(0 1.3频率切片小波逆变换 FSWT实现了信号的时频分析,在逆变换中对原始信号进行了重构,其逆变换为: (5) 实际采样信号X=(x1,x2,…,xN),对其构造m×n阶Hankel矩阵: (6) 式中:N=m+n-1,m≥n。 其奇异值分解表示式为: A=U∑VT (7) 式中:U为m×n阶正交矩阵,UUT=I;V为n×n阶正交矩阵,VVT=I。 E=diag(σ1,σ2,…,σn)是按降序排列的对角矩阵,其对角元素为矩阵A的奇异值。 (8) 式中:μi为AAT的第i个特征向量;vi为ATA的第i个特征向量;σ为A的第i个奇异值。 奇异值序列变化情况由奇异值差分谱bi=σi-σi+1(i=1,2,…,n-1)来描述,相邻两个奇异值变化情况由差分后形成的序列B=(b1,b2,…,bn-1)来反映。两个相邻的奇异值相差越大,它们在整个差分谱中所表现出来的特征也越明显,其前后峰值的变化反映了噪声与有效信号之间不关联的程度,所以选择适当的奇异值有效秩阶次就尤为关键,它可以起到有效剥离噪声、提取有用信号的作用。本文采用文献[10]提出的一种单边极大值原则选取方法,即在奇异值差分谱中从右往左,选择第一个至少单边与其相邻的峰值进行比较,得到差距绝对值最大的峰值点位置,以确定信号的有效秩阶次,从而完成对有用信号的重构和对噪声的消除。 将SVD去噪与FSWT相结合,应用到滚动轴承诊断中,主要步骤如下: ①对原始信号x(t)进行Hankel矩阵重构,根据奇异值差分谱的变化,从右往左,选取第一个峰值变化最大点为重构信号的有效秩阶次;进行降噪处理,分离噪声并提取有用信号。 ②选择频率切片函数,根据信号特征估算频率分辨率和幅值期望响应率,最后计算时频分辨系数k。 ③选择采样频率的一半为频率切片区间,对信号进行FSWT变换,在求取信号的时频分解系数的基础上,得到信号的全频带时频图。 ④针对信号分量在时频图中的分布情况,对能量集中信号区间进行频率切片细化分析,通过分割和重构信号,完成对故障特征的提取。 先建立一个冲击信号,x(t)=e-2πfdtsin(2πfnt+θ), fd=225 Hz,fn=300 Hz,θ=0°。用该信号构造一个重复冲击响应信号来模拟轴承外圈故障。其采样频率为20 000Hz,重复冲击频率fp=80Hz,信号点数为4 096。加入高斯白噪声n(t)后,得到仿真信号y(t),其波形如图1所示。从图1可以看到,强烈的噪声信号覆盖了原信号的冲击响应特征,冲击周期不明显。对该信号进行频率切片分析,其时频图如图2所示。图2中,能量色块分布杂乱,没有明显的排列规律,因此不能确定信号分量分布区域,故障特征提取不成功。 图1 仿真信号时域波形Fig.1 Time domain waveform of simulated signal 图2 仿真信号FSWT时频图Fig.2 FSWT time-frequency of simulated signal 针对频率切片小波对低信噪比信号提取故障能力的不足,本文提出对该类信号先进行奇异值分解降噪,再进行频率切片分析的方法。对原信号奇异值进行分解后,其差分谱如图3所示。自右往左观察图3,在第36点处出现第一个最大单边峰值,且较之左侧相邻点处单边峰值差距最大,选取该点确定重构信号的有效秩阶次,对原始信号进行降噪。 图3 仿真信号奇异值差分谱Fig.3 Singular values differential spectrum of simulated signal 对降噪信号进行频率切片小波变换,得到如图4所示的全频带时频图。 图4 去噪后仿真信号时频图Fig.4 Time-frequency of simulated signal after de-noising 从图4中可看出,整个信号分布主要集中在纵轴3kHz和4kHz处,而且呈点状连续分布,在横轴0~0.2s的时间内规律排列。其中,纵轴4kHz处信号在频率轴上跨度很小,整个呈一细长带状分布,说明该处信号能量分布较弱;纵轴3kHz处信号在频率轴上伸幅较前一信号明显要宽,呈块状连续分布(图中椭圆区域所示),频率范围宽,持续时间短,这正是信号冲击响应的特征,说明这一频率段信号包含了故障特征信息。对3kHz附近的频率切片区间[2.5kHz,3.5kHz]进行FSWT细化分析,得到的时频图如图5所示。 图5 频率切片区间[2.5 kHz,3.5 kHz]的FSWT细化分析时频图Fig.5 FSWT detailed analysis of frequency slice interval[2.5 kHz,3.5 kHz] 从图5中可清晰看到,15条“色带”整齐排列,其反映了信号的冲击响应特征,与设定的故障频率完全相同。 在试验平台上进行滚动轴承试验,试验对象是6205深沟球轴承,其外表面用电火花加工了一个小凹坑,以模拟腐蚀故障。试验采样频率为12kHz,采样点数为4 096,轴的转速为1 730r/min。该轴承的几何参数如表1所示,故障特征频率如表2所示。 表1 轴承几何参数Tab.1 Geometric parameters of bearing 表2 轴承故障特征频率Tab.2 Fault characteristic frequency of bearing 图6是试验振动信号的波形,虽然波形中存在少量冲击脉冲,但无法判断脉冲出现的周期。 图6 实测信号波形Fig.6 Waveform of measured signal 该组信号频谱中没有出现明显的共振频带,对其进行包络谱分析,从中不能发现突出的特征频率成分。对该组实测信号进行奇异值分解,从奇异值差分谱中可看出第58点处单边峰值跟左侧相邻点峰值差距最大,因此,选取该点为重构信号的有效秩阶次进行降噪。对该信号进行频率切片分析,得到图7所示的时频图。从图7中观察整个信号的分布,可以看出在纵轴的5.6kHz、4.8kHz、1.6kHz、1.1kHz处,分别有一条频率范围窄时间连续的直线,说明该处信号能量很弱,不具备冲击响应特征;在纵轴的2.9kHz处有一条频率范围稍宽,时间上呈点状分布,较之3.4kHz处信号强度偏弱许多。这是因为纵轴3.4kHz处信号在频率上分布范围较宽,在时间轴呈不连续分布,持续时间短、间隔时间较长,反映了信号的冲击响应特征。故对其附近区间进行细化分析,得到如图8所示的时频图。 图7 实测信号时频图Fig.7 Time-frequency of measured signal 图8 频率切片区间[3.1 kHz,3.7 kHz]的FSWT细化分析时频图Fig.8 FSWT detailed analysis of frequency slice interval[3.1 kHz,3.7 kHz] 从图8中可观察到,数条深黑色“色带”从左往右排列较均匀,色带跨度范围为3.2~3.5kHz,持续时间约为0.005s,冲击现象非常明显;冲击间隔约为0.01s,这个时间跟轴承外圈故障特征频率103Hz的倒数非常接近,表明该方法提取轴承外圈故障特征成功,理论分析与试验情况相符。 受振动传递路径及背景噪声影响,实测轴承信号中包含的故障特征成分不够多,故障提取相对困难,传统的包络谱解调方法效果欠佳。对振动信号进行频率切片小波变换前,先根据奇异值分解差分谱峰值变换较大点选取合适阶数进行降噪,能从有用信号中有效分离噪声、突出故障特征,有利于时频分析。频率切片小波变换能同时实现信号的时频分析和任意频带信号分量的分割和重构,利用奇异值分解和频率切片分析相结合的方法,能有效提取轴承冲击脉冲。 [1] 冷永刚,郑安总,范胜波.SVD分量包络检测方法及其在滚动轴承早期故障诊断中的研究[J].振动工程学报,2014,27(5):794-800. [2] 刘中磊,于德介,刘坚.基于故障特征频率的阶比双谱方法及其在滚动轴承故障诊断中的应用[J].中国电机工程学报,2013,33(33):123-129. [3] BENRAMDANE S,BOUDRAA A O,CEXUS J C,et al.Time-frequency analysis of pressure fluctuations on a hydrofoil undergoing a transient pitching motion using Hilbert-Huang and Teager-Huang transforms [J].American Society of Mechanical Engineers, 2008(4):199-207. [4] YAN Z,MIYAMOTO A,JIANG Z.Frequency slice wavelet transform for transient vibration response analysis[J].Mechanical Systems and Signal Processing,2009,23(5):1474-1489. [5] YAN Z,MIYAMOTO Z,JIANG Z,et al.An overall theoretical description of frequency slice wavelet transform[J].Mechanical Systems and Signal Processing,2010,24(2): 491-507. [6] 段晨东,高强.基于时频切片分析的故障诊断方法及应用[J].振动与冲击,2011,30(9): 1-5. [7] 钟先友,赵春华,陈保家,等.基于形态自相关和时频切片分析的轴承故障诊断方法[J].振动与冲击,2014,33(4):11-16. [8] 汤宝平,蒋永华,张详春.基于形态奇异值分解和经验模态分解的滚动轴承故障特征提取方法[J].机械工程学报,2010,46(5):37-42. [9] 钱征文,程礼,李应红.利用奇异值分解的信号降噪方法[J].振动、测试与诊断,2011,31(4):459-463. [10]王建国,李健,刘颖源.一种确定奇异值分解降噪有效秩阶次的改进方法[J].振动与冲击,2014,33(12):176-180. BearingFaultExtractionMethodBasedonSingularValueDecompositionandFrequencySliceWaveletTransform Thecapabilityoffaultfeaturerecognitionofthefrequencyslicewavelettransform(FSWT)isweakundertheconditionofstrongbackgroundnoise,inordertosolvethisproblem,afaultfeatureextractionmethodbycombingthesingularvaluedecomposition(SVD)andfrequencyslicewavelettransformisproposed.Firstly,theHankelmatrixisconstructedusingtheoriginalsignal,thentheorderisdeterminedbasedontheprincipleofthesinglesidemaximumvalueofthesingularvaluedifferentialspectrum,andthede-noisingprocessisimplemented.Secondly,thede-noisedsignalisfurtheranalyzedbyFSWTandthetime-frequencymapofthefullfrequencybandisobtained,thedetailanalysisisperformedonthetime-frequencyareawithconcentratedenergy,thenthecorrespondingreconstructedsignalisacquiredbyFSWT.Finally,thefaultfeaturefrequencyinformationofthebearingisextractedeffectivelyfromthereconstructedsignal.Theanalysisresultsofthesimulationsignalandthemeasuredsignalshowthattheaccuratejudgmentoftherunningstateoftherollingbearingcanberealizedbyutilizingtheproposedmethod,anditisofgreatimportantsignificanceforthepracticalengineeringapplication. BearingFaultdiagnosisFeaturerecognitionFeatureextractionSingularvaluedecomposition(SVD)Frequencyslicewavelettransform(FSWT)NoisereductionTime-frequencyanalysisSignalreconstruction 周福成(1977—),男,现为华北电力大学动力机械及工程专业在读博士研究生,讲师;主要从事机械故障监测与诊断方向的研究。 TH13;TP29 A< class="emphasis_italic">DOI :10.16086/j.cnki.issn1000-0380.201610006 河北省自然科学基金资助项目(编号:E2014502052); 中央高校基本科研业务费专项基金资助项目(编号:2014MS154、2015XS120)。 修改稿收到日期:2016-02-01。2 奇异值分解原理
3 基于SVD去噪与FSWT的时频分析方法
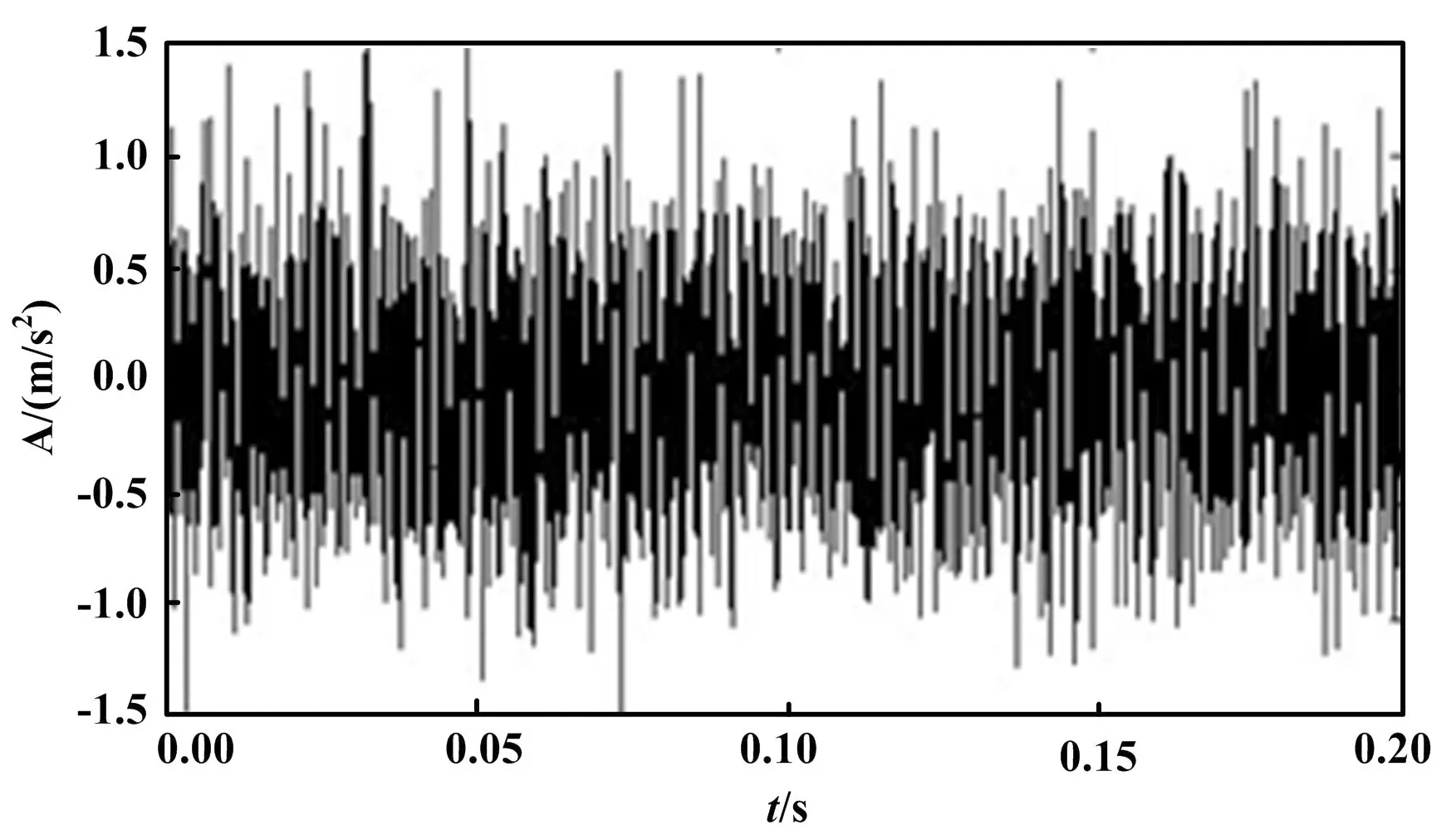
4 仿真信号分析
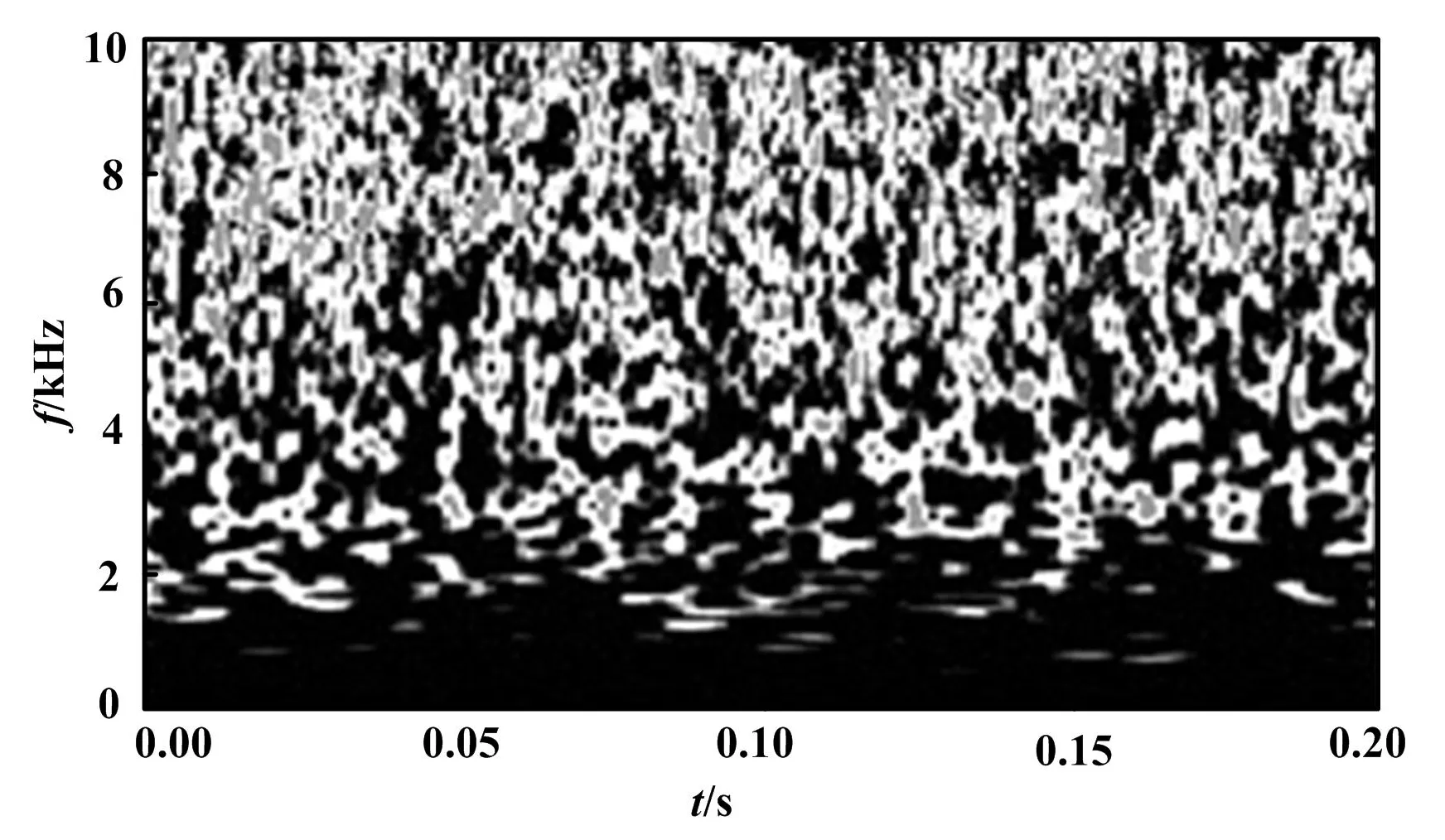
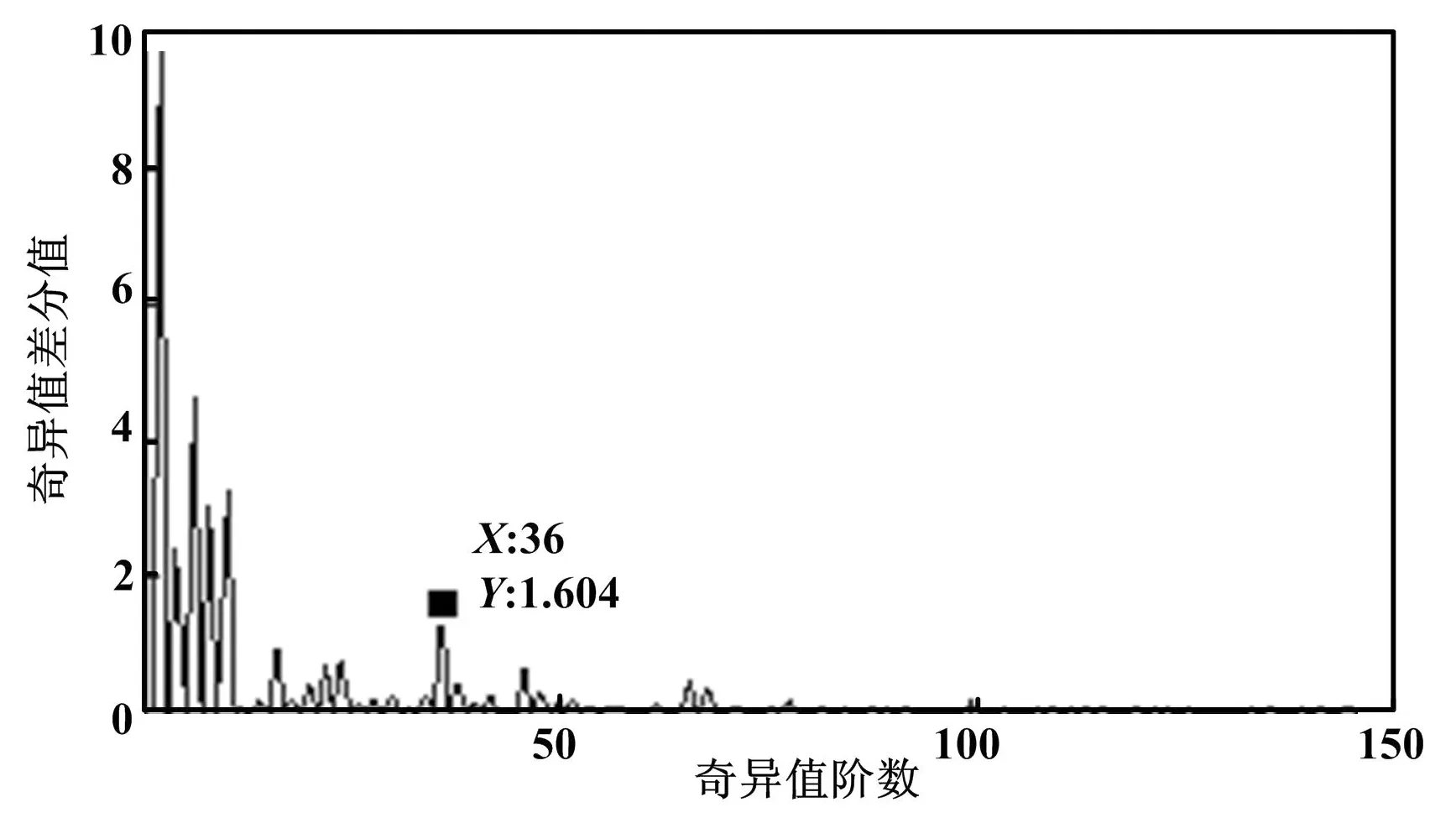

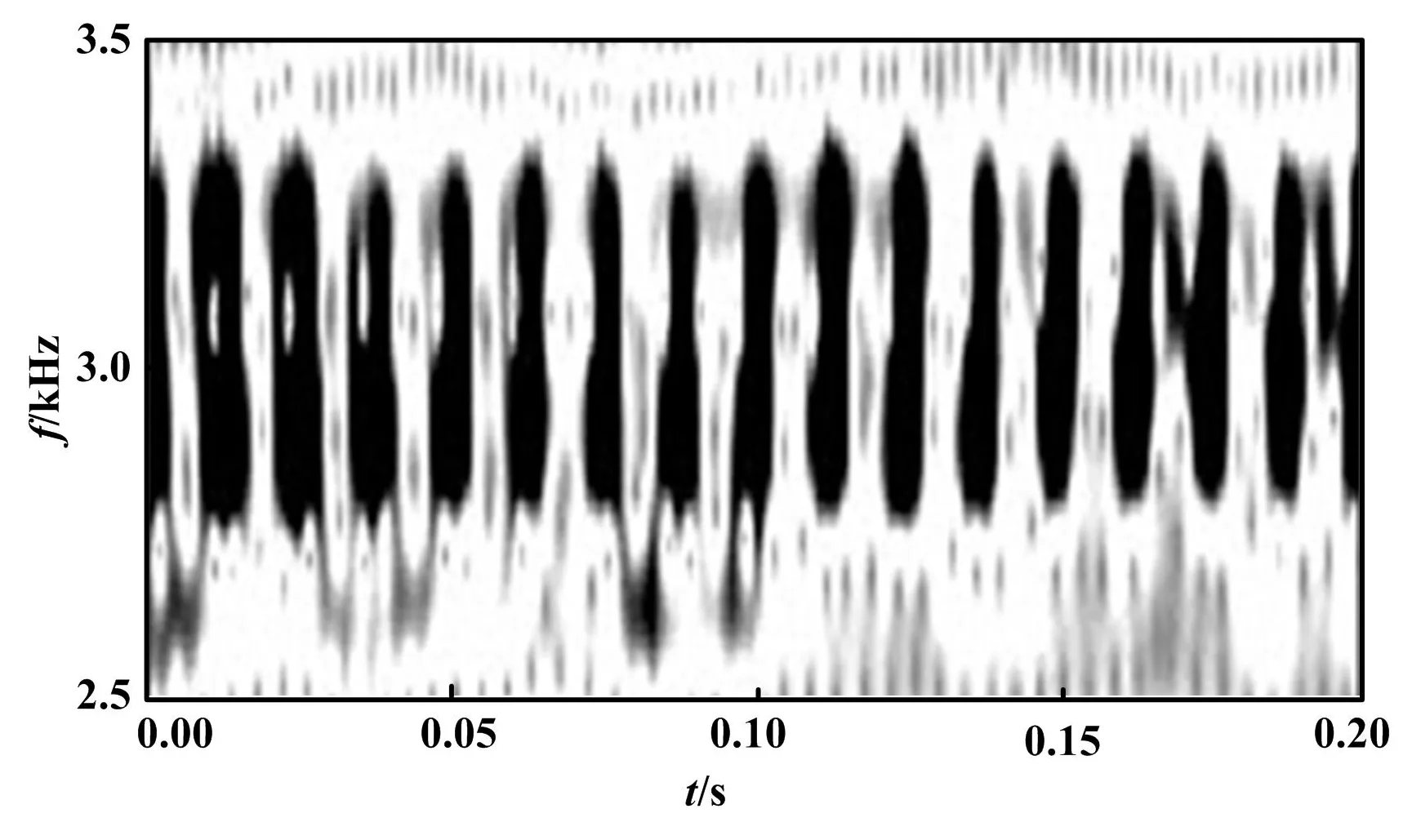
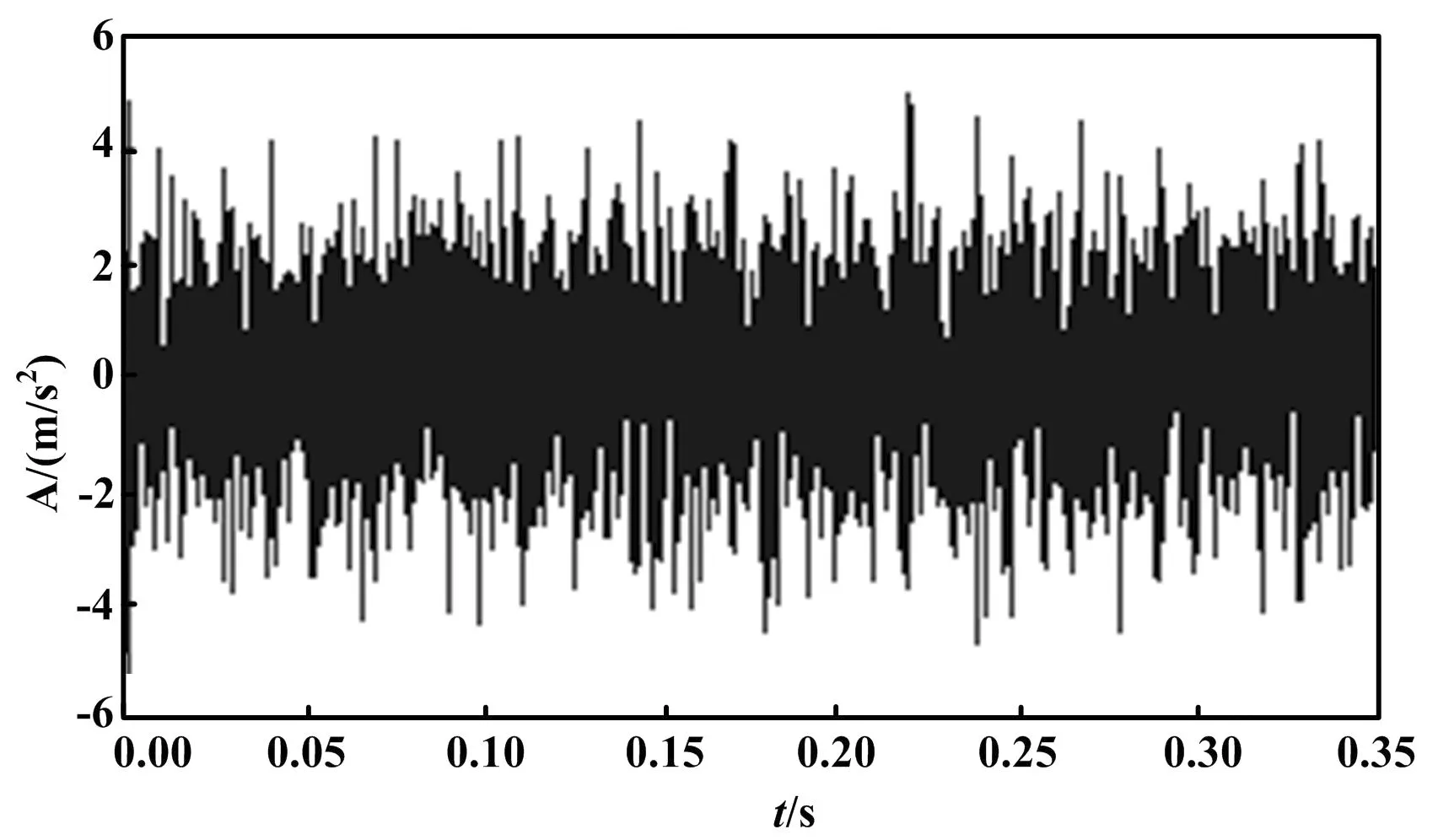
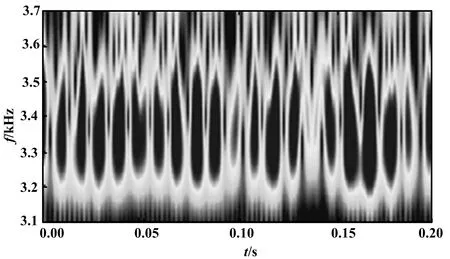
5 试验信号分析



6 结束语

