球磨机灰色预测无模型自适应控制策略
马 光 李 栋 杨晓冬
(北华航天工业学院电子与控制工程学院,河北 廊坊 065000)
球磨机灰色预测无模型自适应控制策略
马光李栋杨晓冬
(北华航天工业学院电子与控制工程学院,河北 廊坊065000)
球磨机负荷控制系统是一个具有大时滞、强时变性、强非线性及多变量与强耦合等特性的复杂系统。为了更好地克服球磨机负荷控制系统中存在的大滞后和不确定性等问题,提出了灰色预测无模型自适应控制(MFAC)策略。在控制系统下,分别采用PID、灰色预测PID、MFAC及灰色预测MFAC进行控制仿真分析。实际应用验证了该策略的可行性与合理性,表明了灰色预测无模型控制策略具有良好的控制性能和实用价值。
球磨机无模型自适应控制灰色预测优化时滞性不确定性鲁棒性抗干扰
Anti-interference
0 引言
钢球磨煤机简称球磨机,是目前我国火电厂制粉工序中的重要磨粉设备。球磨机的良好运转有利于火电厂的正常运行。球磨机是一个拥有大时滞、时变性、非线性以及多变量等特点的复杂控制系统。如果直接对其进行控制,不易达到预期的控制效果。球磨机的负荷控制是一个相对较独立的控制系统[1],可以就该控制系统单独进行研究。
通过研究球磨机负荷控制系统[2],针对工业生产过程中系统的不完全性、大滞后等特点,结合无模型自适应方法与灰色预测理论,提出灰色预测MFAC控制策略。利用Matlab7.1软件,分别在一般离散时间线性系统、非线性系统、大时滞系统以及带干扰的非线性系统中进行仿真研究。验证了灰色检测无模型自适应控制策略相对于经典控制方法PID、灰色预测PID[3]以及传统MFAC在快速性和鲁棒性能方面的优势,证明了这种灰色预测无模型自适应控制策略的有效性和合理性,且该灰色预测无模型自适应控制效果优于其他三种控制策略。
1 无模型自适应控制
无模型的控制器在设计过程中利用与常规控制器不同的方法来得到系统的参数模型,然后再进行控制器的设计。无模型的建模是在反馈过程中进行的。这种方法建立的初始模型可以不准确,但其控制律必须具有稳定性和收敛性。
无模型自适应控制方法是由参数估计算法和无模型控制律[4-6]算法在线交替组合形成的。其根据受控系统的输出与输入数据,估算出其泛模型中的特征参数值,是一种反馈的方法。在一轮控制之后,根据反馈得到新的数据,再进行新的建模控制,然后开始下一轮的控制,如此反复循环,可得到精准的数学模型。此方法有效避免了一些复杂的数学模型,在实际工业生产过程中起着很大的作用。
1.1泛模型与特征参量
一般的单输入单输出(singleinputsingleoutput,SISO)离散时间的非线性系统如下:
y(k+1)=f[y(k),…,y(k-ny),
u(k),…,u(k-nu)]
(1)
式中:y(k)、u(k)分别为上述离散时间系统中k时刻的输出值与输入值;n∈R+、ny∈R+分别表示输出和输入的阶数,且都是未知的。以此系统为特例,推导出模型结构,有以下三个假设[7]。
①上述离散系统公式(1)的输出和输入,要求具有可观测性,同时也是可控的。即对于被控系统,如有界的期望输出信号y*(k+1),必定也有着与之对应的有界可行控制的输入信号,使此系统的实际输出值等于期望得到的输出值。
②关于系统控制过程中的输出u(k)的偏导为连续状态。
③系统符合广义的Lipschitz条件,也就是说,对于所有的非负值,当满足k1≠k2且输出量不相等时,有:
|Δy(k+1)|≤b|Δu(k)|
(2)
式中:y(k1+1)-y(k2+1)=Δy(k+1);u(k1)-u(k2)=Δu(k) ;b为一个大于零的常数。对于一个非线性系统,在符合①和②的情况下,当输出变化量u(k1)-u(k2)≠0时,会存在一个参数φ(k)∈R,即为特征参数,也可称为偏伪导数。
由此可得如下数据模型:
Δy(k+1)=φ(k)Δu(k)
(3)
式中:|φ(k)|≤b,b为正常数。数据模型式(3)为系统式(1)的泛模型形式,φ(k)称为特征参数。
1.2无模型控制律
1.2.1无模型控制律基本形式
无模型控制律的基本形式为:
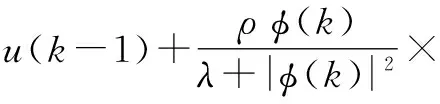
[y*(k+1)-y(k)]
(4)
式中:ρ为步长因子,ρ∈(0,1]。步长因子的加入使此控制算法更具有普遍性。同时,由于式(4)中的λ对系统的输入和输出有很大影响,因此其不可随意加入,其值的大小也不可随意给出。首先,λ的加入对输入变化量Δu(k)具有限制作用,令输入信号变得更加平滑;其次,很多仿真研究表明,λ的值对受控系统的稳定性和鲁棒性都有很大的影响。
1.2.2伪偏导数估计算法
伪偏导数估计算法表示为:
J[φ(k)]=|y(k)-y(k-1)-φ(k)Δu(k-1)|2+
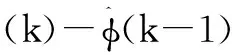
(5)
式中:μ称为权重因子或惩罚因子。
式(5)关于φ(k)的极值为:
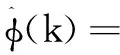

(6)
式中:η为步长因子,其范围为(0,1]。与式(4)中的ρ相同,步长因子η的加入使此控制算法更具有普遍性,应用时更加灵活。
1.2.3无模型自适应控制
将以上两种算法结合,可以得到以下无模型自适应算法:
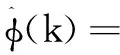
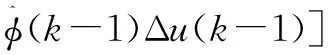
(7)
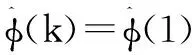
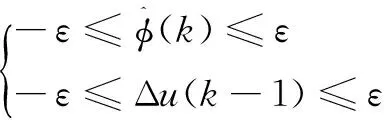
(8)
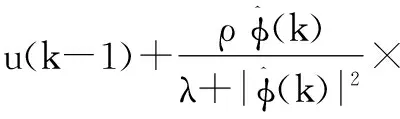
[y(k+1)-y(k)]
(9)
式(7)控制律算法与式(9)参数估计算法在线交替组合,形成无模型自适应控制(model-freeadaptivecontrol,MFAC)。该算法可根据系统的输入量与输出量,估算出特征参数φ(k)的值。在控制的过程中,这种算法是反馈于受控系统的。在进行一轮完整的控制之后,就可以得出最新的观测数据。将这些新的观测数据加入到历史数据中去,利用这些数据不断地估计出最新的特征参数值。如此一直循环下去,即可完成整个系统的控制。MFAC的核心思想是辨识与控制一体化,虽然MFAC不依赖于受控对象数学模型的建立,但在实际的受控系统中,模型还是存在的。MFAC原理如图1所示。
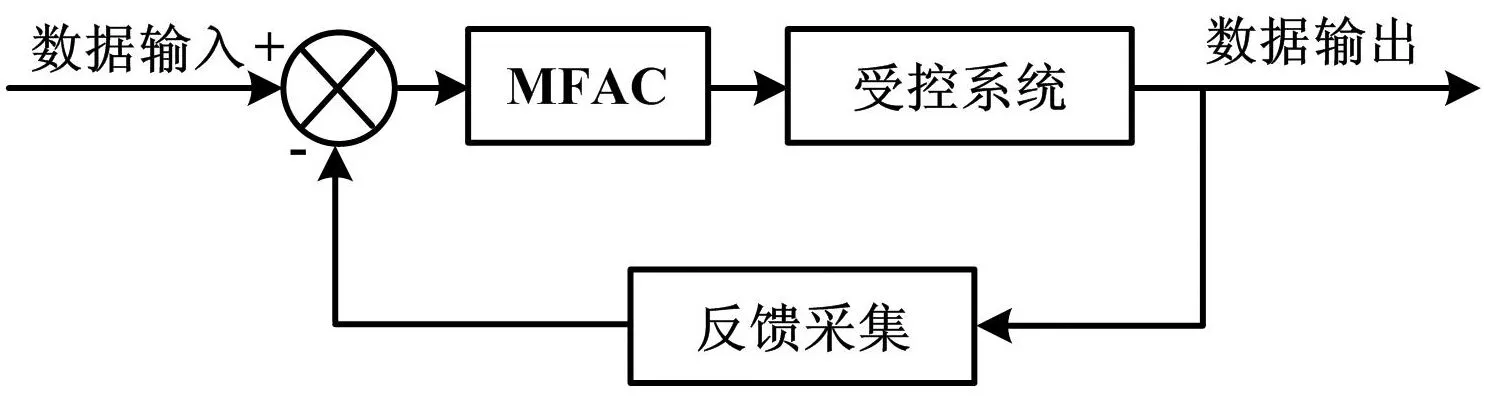
图1 MFAC原理框图Fig.1 Schematic diagram of MFAC
2 灰色预测模型
灰色预测理论[8]于1982年被我国学者邓聚龙首先提出,这一理论讲述的是一种全新的预测方法。与此同时,灰色预测控制[9]就是将预测理论与自动控制理论相结合的预测控制方法。系统通过将数据进行分析处理,总结出系统规律,对有可能发生的情况进行预测并及时作出处理,做到防患于未然,大大提高了系统的鲁棒性。
灰色模型GM(C,D)是由微分方程组合而成的动态预测模型。本文主要讲述GM(1,1)模型,其由单变量-单阶的微分方程构成。本文中,灰色预测程序使用S-function函数编写,并封装成GM(1,1)模块。
模型原始建模序列:G(1)={g(0)(1),g(0)(2),…,g(0)(h)}。h表示建模维数,由于它是信息不完整的灰色量,所以具有一定的随机性。令G(1)为g(0)的历史数据累加形成的序列:
G(1)={g(1)(1),g(1)(2),…,g(1)(h)}
在所得数据的基础上,利用线性动态模型对其进行数据拟合和数据逼近,得到一个微分方程,这个方程就是GM(1,1)的模型:
(10)式中:b为发展系数;c为灰色作用量。现在令j(0)(k)=-0.5g(0)(k-1)-0.5g(0)(k),k=2,3,…,h。用最小二乘法求得系数的值,向量形式记作:
γ=(bc)T=(DTD)-1DTβ
(11)

GM(1,1)模型微分方程的解为:g(1)(k+1)=[g(0)(k)-c/b]×exp(-bk)+c/b
(12)
式中:k=0,1,…,h-1
当原始数据预测步数为N时,即在(k+N)时刻,预测公式为:
g(0)(k+N)=[g(0)-c/b]×
exp(-bN)[1-exp(-b)]
(13)
3 灰色预测与无模型自适应控制结合
无模型自适应控制方法是在系统时滞已知且不变的理想假设基础上提出的。但是这种假设太过理想,在实际的工业生产过程中,很多受控系统是大时滞系统。对于不断变化的大时滞系统,无模型自适应控制很难实现理想、有效的控制。在本文中,将灰色预测模型GM(1,1)与无模型自适应控MFAC模型相结合,克服了系统的延迟和不确定性等一系列的问题。GM(1,1)模型[8-9]与MFAC控制相结合,是在原有的无模型自适应控制原理中,将GM(1,1)模型添加到MFAC的反馈回路中,以超前预测补偿系统因参数发生时变或时滞延迟等造成的一系列不确定性,从而组合得到一种新的控制律。该控制律可进一步改善MFAC的控制效果。在原有MFAC的反馈中加入预测模块,将原有的输出g(k)读入记作g(0)(k)。在反馈回路中,GM(1,1)将(k+N)时刻的预测值g(0)(k+N)代替原有回馈值g(0)(k),并与原有的输入设定值r(k)相比较,产生的偏差记作e(k),作为输入信号输入到MFAC控制器中。MFAC控制的输出量作为被控对象的输入,记作u(k)。灰色预测MFAC系统原理图如图2所示。
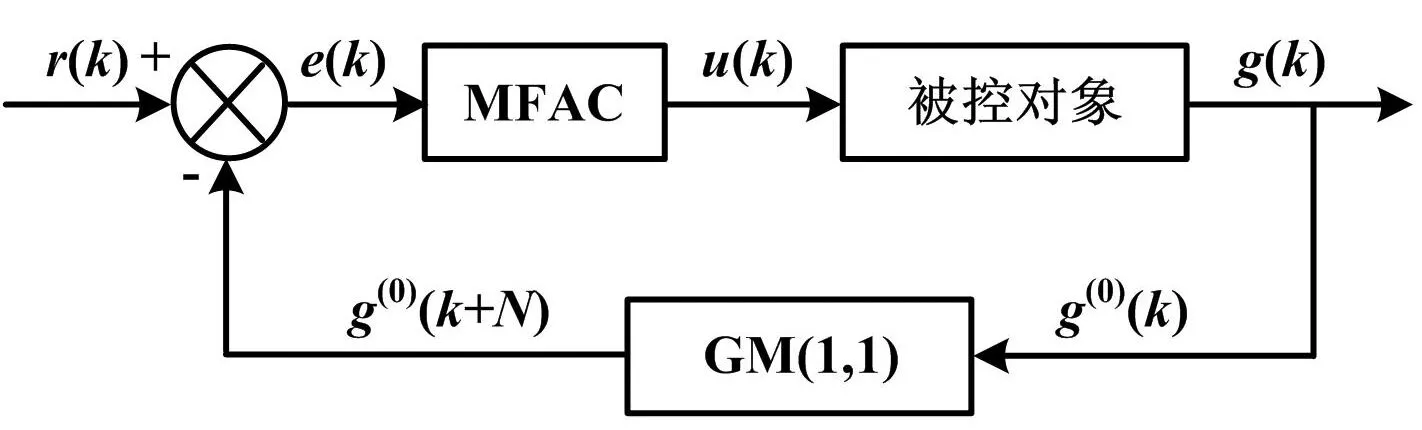
图2 灰色预测模型下的MFAC的原理图Fig.2 Schematic diagram of MFAC under gray prediction model
4 负荷控制系统的仿真研究
4.1球磨机负荷控制系统的数学模型
球磨机的负荷控制是一个相对独立的控制系统[1]。通过对其进行阶跃响应试验,得到球磨机负荷控制的数学模型[10]:
(14)
式中:τ为数据模型中的纯延迟。
本方案为了论证灰色预测MFAC控制的有效性和优越性,分别采用PID控制、灰色预测PID控制、MFAC及灰色预测MFAC四种方案,对球磨机负荷控制系统进行了仿真研究。
4.2仿真结果分析
①首先在仿真之前进行控制器的参数设置:设定输出为g(k);输入为u(k);初始输入值u(1)=u(2)=0;初始输出值g(1)=g(2)=g(3)=0。
②对MFAC进行参数设置:伪偏导数φ(1)=0.2;学习因子为0.008;惩罚因子为0.1。
③对灰色预测GM(1,1)模块进行参数设置:建模维数选择h=5;采样周期T=1s;预测步数N=13;预测控制开始时刻k=50。
④对PID控制进行参数设置:比例环节Kp=1.2;积分环节Ki=0.046;微分环节Kd=40。
当输入信号为单位阶跃时,灰色预测MFAC效果最好,其调节时间短,基本无超调;其次是MFAC控制,稳定时间比灰色预测MFAC长,但基本没有超调,品质良好;再次为灰色预测PID控制,其控制效果最不理想。
待控制稳定之后,在500 s时外部加入幅值为0.4的定值阶跃。在二次阶跃时,四种控制策略的恢复稳定的情况与首次前500 s的仿真情况基本一致。灰色预测MFAC控制策略的效果仍是最优的,可以快速地恢复到稳定状态。
当球磨机负荷控制系统加入幅值为0.002的正弦信号作为干扰时,PID控制的抗干扰能力不如其他三种方案。灰色预测PID控制方案虽然相对于单独PID控制效果得到些改善,但仍较不理想。灰色预测MFAC控制效果最为平滑、快速且基本无阶跃产生。综合来说,灰色预测无模型自适应控制策略的控制效果最为优秀[11]。
5 结束语
针对球磨机负荷控制系统的大时滞和不确定问题,提出了以灰色预测无模型自适应控制策略来进行自适应参数的优化;其超调小、鲁棒性好,抗干扰能力也远优于其他三种控制方法,能很好地解决非线性、适应性以及大时滞、延迟等问题,为今后解决类似系统的问题提供了新的思路和方案。
[1] 侯典来.12MW机组磨煤机的智能控制[J].自动化仪表,2006,27(1):32-35.
[2] CHENG Q M,ZHENG Y.Control system of Multi-model PID neuronnetwork for ball mill[J].Proceedings of the CSEE,2008,28(2):103-109.
[3] CHENG Q M,MIN L C,LI Q,et al.Study of a grey PID control system for ball mill load in a thermal power plant[J].Journal of Engineering for Thermal Energy and Power,2009,24(5):630- 634.
[4] HOU Z S.Thesituationand prospects of model-free adaptive control[J].Control Theory and Applications,2006,23(4):586-592.[5] HAN Z G.Study on non-modeling control method for a class of complex systems [J].Control and Decision,2003,18(4):398-402.
[6] HAN Z G,WANG G Q.Cascade scheme of model freecontrol law and its application [J].ACTA Automation Ainica,2006,32(3):345-352.
[7] ARTUR A,MAARJA K.Design of a shape-changing anthropomorphic mannequin for tailoring Applications[C]//International Conference on Advanced Robotics,ICAR 2009,Munich,Germany,2009.
[8] 刘今越,曾周末,李铁军.基于灰色预测-模糊逻辑的磁场测量采样技术研究 [J].仪器仪表学报,2010,31(1):122-126.
[9] 彭勇刚,韦巍.注塑机机械手位置伺服系统灰色预测PID及迭代学习混合控制 [J].仪器仪表学报,2008,29(1):2062-2066.
[10]HUANG C C,YU X J,LV Z Z.Ball mill load control based on gray prediction PID control [J].Process Automation Instrumentation,2007,28(3):62-64.
[11]党宏社,张颖,王刚.球磨机控制系统的设计[J].自动化仪表,2014(4):26-29.
GrayPredictionModel-freeAdaptiveControlStrategyofBallMill
Theballmillloadcontrolsystemisacomplexsystemfeaturinglargetimehysteresis,time-varying,strongnonlinearity,multivariableandstrongcoupling.Inordertofurtherovercomethelargetimelaganduncertaintyandotherproblemsofsuchloadcontrolsystem,theschemeofgraypredictionmodel-freeadaptivecontrol(MFAC)isproposed.Forthiscontrolsystem,PID,graypredictionPID,MFAC,andgraypredictionMFACarerespectivelyappliedinsimulationanalysis.Theapplicationsverifythefeasibilityandrationalityofthisstrategy,anditisindicatedthatgraypredictionmodel-freeadaptivecontrolhasgoodcontrolperformanceandpracticalvalue.
BallmillModel-freeadaptivecontrolGraypredictionOptimizationTimehysteresisUncertaintyRobustness
马光(1974—),男,2007年毕业于天津理工大学控制理论与控制工程专业,获硕士学位,副教授;主要从事智能控制方向的研究。
TH-39;TP273+.2
A< class="emphasis_italic">DOI
:10.16086/j.cnki.issn1000-0380.201610007
北华航天工业学院科研青年基金资助项目(编号:KY-2015-05);
北华航天工业学院科研重点基金资助项目(编号:ZD-2014-07)。
修改稿收到日期:2016-04-21。

