复杂岩基上重力坝抗滑稳定计算方法研究
黄灵武 王 衎 杨宗宇
(国核电力规划设计研究院,北京 100095)
复杂岩基上重力坝抗滑稳定计算方法研究
黄灵武王衎杨宗宇
(国核电力规划设计研究院,北京100095)
介绍了两种计算复杂岩基上重力坝抗滑稳定的方法,即刚体平衡法与有限元法,并通过算例,对两种计算方法进行了比较评价,得出了两者之间的关系,为选择适宜的计算方法提供了依据。
重力坝,刚体极限平衡法,有限元法,安全系数
0 引言
刚体极限平衡法和有限单元法是目前较多采用的坝基抗滑稳定安全度的两种计算方法。刚体法概念清楚,计算简便,工作量小,有丰富工程经验,而且有比较成熟的与之配套的设计准则,是现行规范推荐的方法,但它只能对坝基的稳定性作笼统的分析,不能确定滑裂面上的应力分布,因而也就不能探索破坏的机理及其变化发展过程。对于复杂基础,一般采用加权平均法来核算抗滑稳定安全系数,但由于该方法缺乏较强的理论依据,用该方法无法界定真实的稳定安全系数, 必须尽可能地搜索最小安全系数,否则可能导致不安全的计算结果。有限单元法已成为分析复杂地基问题的有力工具,它不但可以分析断层、节理、裂隙、破碎带等地质缺陷的影响,而且可以将水工建筑物的应力、变形、渗流和稳定问题等结合在一起分析,由此了解整个系统的破坏机理。有限元法可以较为可靠地确定地基内的应力及变形情况,了解沿软弱带的破坏区域和错动值。然而现阶段,对有限元法计算结果的认识尚未统一。
本文将对复杂地基上重力坝抗滑稳定的两种计算方法进行综合评价,得出它们之间的相互关系,从而评价出这两种方法的优劣。
1 基本理论
如图1所示是坝基为多种岩体组合时的重力坝的示意图。
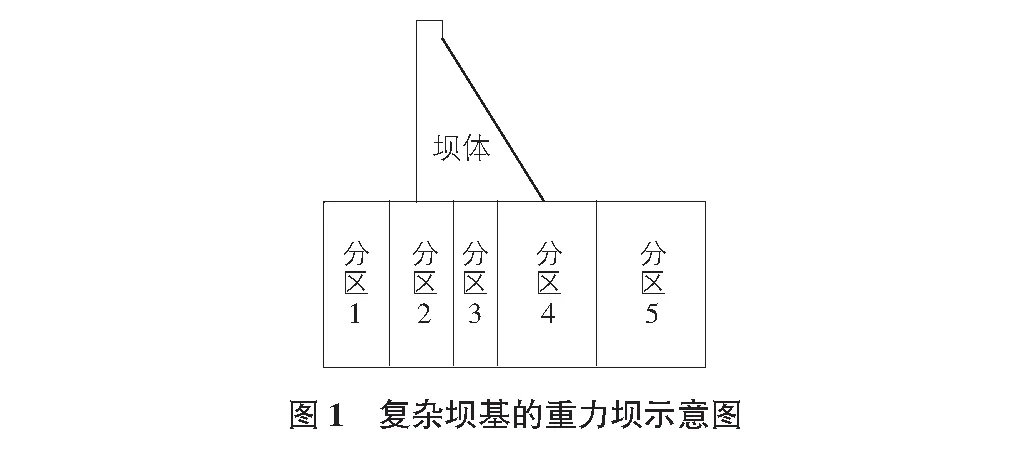
若坝体和地基为均质的,则沿建基面的抗滑稳定计算公式为:
(1)
式中:Kc——沿坝基面的抗滑稳定安全系数;
W,P——坝基面上的法向合力和合剪力;
A——滑面面积;
f′,C′——坝基面的抗剪断参数。
若坝基为复杂地基,如图1所示,建基面下有n种岩性材料,可将式(1)推广为:
(2)
式中:Wi,Pi——第i段的法向合力和合剪力;
Ai——第i段的面积;
f′,C′——第i段的抗剪断参数。
对于体型、荷载确定的重力坝,其W=∑Wi,P=∑Pi是固定不变的。 一般可采用面积加权的方式计算出建基面在平均意义下的C′和f′,用式(1)得到安全系数。
采用有限元计算时,为了方便统计建基面上的法向力和剪力,可在建基面上设置一层Goodman[1]节理单元,通过应力积分,用式(2)求得安全系数。
2 简单算例
以一平面问题作为研究对象进行分析。如图2所示,假设某重力坝的地基由一软一硬两种岩体组成。其坝高50 m,底宽35 m,顶宽7 m,上游铅直,下游转折点处高程45 m。坝体和地基的材料参数如表1所示。

表1 材料参数

材料弹模/GPa泊松比凝聚力C/MPa摩擦系数密度/t·m-3混凝土(坝体)250.1671.661.342.64软材料(分区1)10.350.10.472.40硬材料(分区2)50.30.60.702.50
地基计算范围取向上、下游各延伸80 m,由建基面向下取80.0 m。建立如图3所示的平面有限元网格,其中单元数为2 088,节点数2 205,并在地基和坝体的接触面设置了一层共35个长1 m,厚0.2 m的Goodman单元。为了更好地分析规律,对分区1的宽度L取不同的长度进行计算。考虑了L分别取0,40,60,75,80,85,90,95,100,105,110,115,120,140,160,195共16种情况。
计算时不考虑渗流的作用,取上游水位45.0 m,下游水位15.0 m。对于不同的材料分区,分别采用刚体极限平衡法、弹性有限单元法和弹塑性有限单元法(采用D-P屈服准则)计算,对比其所得的安全系数,见表2。
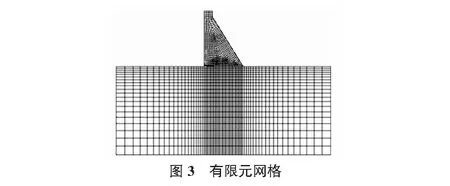
表2 刚体法和有限元法计算所得安全系数

L刚体法弹性弹塑性弹性—刚体法偏差/%弹性—弹塑性偏差/%04.489004.452654.45261-0.810-0.001404.489004.604444.507922.572-2.096604.489004.607564.580302.641-0.592754.489004.608494.552312.662-1.219804.489004.608004.607932.651-0.002854.237004.279124.282350.9940.075904.105813.916353.92236-4.6140.153953.721793.499503.51453-5.9730.4291003.337762.932863.00386-12.1312.4211052.953732.435322.55636-17.5514.9701102.569701.997352.13916-22.2737.1001152.185671.542181.64217-29.4416.4831201.801651.611281.72982-10.5667.3561401.801651.707441.83194-5.2297.2921601.801651.786261.84356-0.8543.2081951.801651.850671.859712.7210.489
从表2中可以看出,当坝体处于复杂地基上时,当L<90 m时,除个别情况外,刚体法得到的安全系数较弹性有限元法得到的安全系数小,且相差在2.7%以内,当L>90 m时,除个别情况外,刚体法得到的安全系数大部分较有限元法得到的安全系数大,且相差较大,最大相差29.4%;当L<100 m时,弹性和弹塑性有限元法所得结果相差在2.1%以内,而当L>100 m时,弹性和弹塑性有限元的结果部分相差较大,最大相差7.4%。文献[2]提到采用线性应力和非线性应力得到的安全系数差别较小,在1%以内,是由其考虑工况较少引起的,与本文L取85 m时所得结果相类似,具体情况有待进一步验证。
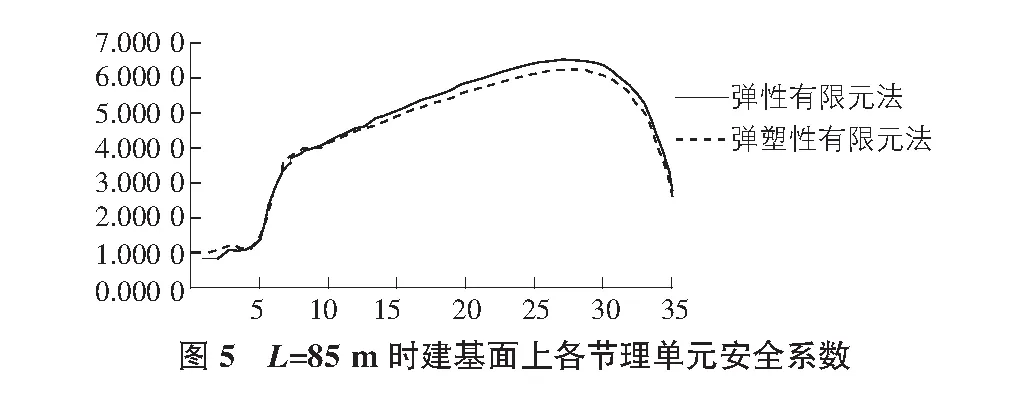
取L=80 m,85 m,90 m,95 m四种典型复杂地基,分别计算各节理单元的安全系数,见图4~图7。
可以看出,弹性和弹塑性有限元计算结果在大部分节理单元处相差较小(4.5%以内),在坝踵单元处相差较大,最大达46.389%。在软硬材料交界面上对应的安全系数最低,L=95时坝踵与坝址处由于应力奇异,安全系数异常大,计算整体安全系数
时应排除这些奇异单元。



3 结语
本文研究了重力坝抗滑稳定安全系数常用的计算方法:刚体极限平衡法、弹性有限元和弹塑性有限元法之间的关系。通过简单算例表明,刚体极限平衡法由于没有考虑到应力分布的不均匀性,其计算结果较有限元的结果要大;刚体法已应用多年,相应的规范也较为成熟,应用有限元得到的安全系数而套用刚体极限平衡法的规范来使用偏于保守;而弹性和弹塑性有限元法所得到的安全系数在一定范围内相差不大。
[1]Goodman R E,Taylor R L,Brekke T L.A model for the mechanics of jointed rock[J].Journal of the Soil Mechanics and Foundations Division,American Society of Civil engineering,1968,94(SM3):638-659.
[2]杨强,肖平,薛利军.复杂坝基重力坝抗滑稳定分析中应力状态研究[J].水力发电,2006(12):26-29.
Study on anti-sliding stability calculation of gravity dam on complicated foundation
Huang LingwuWang KanYang Zongyu
(StateNuclearElectricPowerPlanningDesignandResearchInstitute,Beijing100095,China)
The paper introduces two kinds of gravity dam anti-sliding stability computation methods on the complex rock foundation which includes rigid body limit equilibrium theory and finite element method. Through computation examples, it compares and evaluates the above-mentioned computation methods, and obtains their relationship, which has provided some basis for selecting suitable computation methods.
gravity dam, rigid body limit equilibrium theory, finite element method, safety coefficient
1009-6825(2016)23-0072-02
2016-06-04
黄灵武(1984- ),男,工程师
TU331.4
A

